# (8) 最優控制與規劃 > 作者：[謝天](https://www.zhihu.com/people/xie-tian-55-77) > > 來源：[POST 館](https://zhuanlan.zhihu.com/c_150977189) ## 基于模型的增強學習方法 在之前的[增強學習簡介](https://zhuanlan.zhihu.com/p/32598322)之中，我們已經了解了我們的增強學習問題的一般結構是：給定一個狀態，策略函數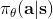可以由某種含參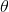的結構（如策略梯度法和演員-評論家算法使用顯式的策略網絡，值函數方法的策略是隱式的）確定，并通過這個策略函數得到一個行動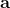，將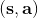共同輸入給環境，環境通過某些轉移概率函數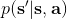，得到新的狀態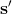，形成一個循環。根據 Markov 性，軌跡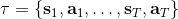的發生概率為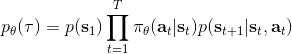，是由我們掌握的策略函數和環境掌握的轉移概率共同決定的。增強學習問題的目標是最大化總收益函數的關于軌跡的期望，一般來說就是得到一組最優的參數使得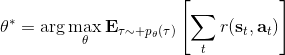。我們在前幾篇中主要介紹了無模型 (model-free) 的深度增強學習算法，這些算法的主要特征是不假設我們知道初始分布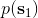和轉移概率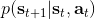：在一般的問題中，這些概率是非常難知道的；這些無模型方法可以很好地繞開這些不知道的東西，我們甚至不嘗試去學習這些轉移概率。 在一些問題中，我們可以假設我們知道系統的轉移概率 (dynamics) 。最簡單地，我們設計一個 AI 來下棋（如圍棋，棋類的規則是眾所周知的）；很多系統是容易建模的，如給汽車設計一個導航系統（不是具體的駕駛行為，而是站在比較高角度的路徑規劃，這個就會相對容易很多，各種地圖上已經有很完善的類似功能了）；更具體地，我們可能會在一個模擬器中研究諸如機器人運動和視頻游戲的問題，我們可以通過模擬器得到下一個狀態到底是什么。退一步說，即便我們不知道轉移是什么，但我們在很多問題中也可以學出這些轉移。比如在系統識別 (system identification) 問題中，我們已經有一個模型結構（如機器人的結構已知）了，需要通過學習去擬合里面未知參數（如機器人的各部分質量和摩擦系數等）；更廣泛地，我們可能會去用觀察到的轉移數據去擬合一個廣義的模型（比如神經網絡或者高斯過程）。 那么這些轉移概率是毫無用處的么？如果我們能知道這些轉移概率，通常問題就會變得簡單很多。不同于無模型的方法，基于模型的 (model-based) 增強學習方法通過學習轉移概率來決定如何選擇行動。在這一篇中，我們將先介紹如果我們完全知道轉移概率，如何進行行動決策（最優控制、軌跡優化）；之后，我們再去關注如何去學習未知的轉移概率，以及如何通過諸如模仿最優控制的方法學習策略。 讓我們先忘記策略這個東西的存在。類似[之前](https://zhuanlan.zhihu.com/p/32575824)人在老虎面前的決策問題，我們需要給出一連串決策，使得被老虎吃掉的概率最小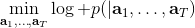：，這類問題通常能轉化為一個最小化代價的問題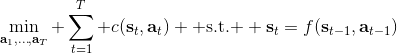：，或者是最大化收益。我們假設環境是確定的，目標是最大化收益問題，那么問題的結構就變成了環境向智能體給出了初始狀態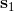，然后智能體做出一系列的行動決策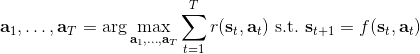，直接交給環境。在確定性環境下，我們上面做的就是一個最優控制了；而對于環境是隨機的情況下，軌跡條件概率為（注意是我們給定行動決策序列之后，狀態序列的概率），我們一下子做好的期望收益最大的**開環** (open-loop) 控制系統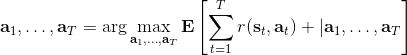就不見得是最優的了：因為我們通常沒有必要一下子把所有的決策全部做了，可以通過做第一個決策來觀察之后是什么樣的隨機情況這樣的反饋機制，來繼續做后面的決策，使得接下來的決策做得更好。這樣的機制通常被稱為**閉環** (closed-loop)。下圖說明，區別在于開環系統在一開始就把所有決策單向傳遞給環境，因此不接受反饋；閉環系統則每次只傳遞單次行動，并接受下一個狀態作為反饋。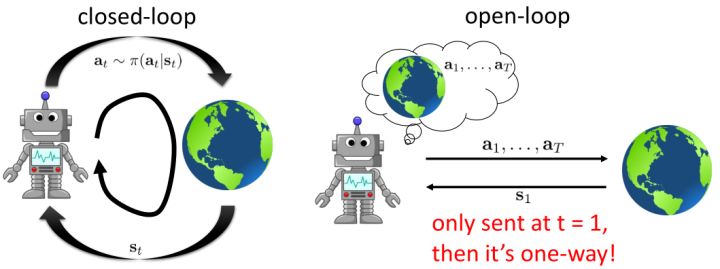  在一個閉環控制系統中，我們就需要一個策略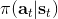了，在策略的加持下，我們的軌跡概率就變成了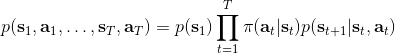；我們需要做的是得到一個最優的策略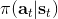，使得期望收益最大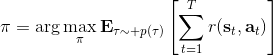：。關于這個策略簇，我們在之前提到的主要是用一個神經網絡來確定，此外在這一篇中我們還將提到使用經典的軌跡優化 (trajectory optimization) 方法來訓練一個（時變的）線性策略簇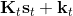，基本上就是主要執行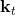，并使用當前給定狀態做出一些線性修正。因此，根據我們限定的策略簇不同，策略的學習可以從非常簡單到非常復雜。 ## 交叉熵方法 (CEM) 我們的第一類規劃算法是隨機優化，通常用于時長比較短的問題。讓我們先將之前的控制問題進行一些抽象，如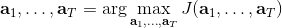，其中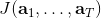是某種函數，我們并不關心具體是什么，只是想把它最大化；再進一步把決策序列寫成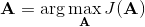。（_ 因為在這邊我們的決策只能決策行動，決策和行動是一碼事，在后文中，我們將 action 行動和 decision 決策混用 _）在上一篇講 Q 學習的連續控制中，我們也提到了這類算法中最簡單的是從某種分布（如均勻分布）中挑選若干個決策序列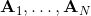，然后選取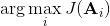。這樣的算法在低維問題中還是有一定效果的，有時候被稱為隨機打靶法 (random shooting method)。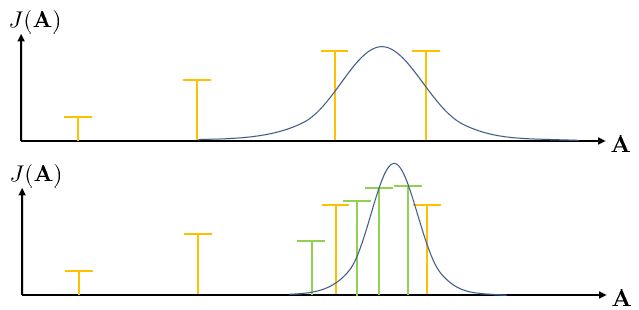  這種方法的一個改良版本稱為**交叉熵方法** (Cross-entropy Method, CEM)，對 30 到 50 維這樣的問題效果不錯。在之前的隨機打靶法中，我們需要從某種分布中選取決策序列，但是關鍵問題是，我們使用哪一種分布？在一開始，我們對于如何選擇沒有任何先驗知識，所以采用某種均勻的先驗分布。經過一把采樣之后（如上圖的四個采樣），我們發現有一些樣本效果比較好，于是我們選出幾個較好的樣本，來擬合一個分布（如采用圖中的高斯分布），作為下一次采樣的先驗分布。通常認為這樣的分布抽樣效果會比之前的要好，但是對于很病態的問題我們也沒什么太好的辦法。第二次采樣（下圖）進一步更新分布。對于連續值輸入的交叉熵方法，算法可以描述成以下步驟的循環： 1. 從先驗分布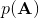中抽樣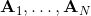：。 2. 計算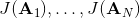。 3. 選取一個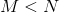（也可以選一個比例），挑選出 J 值最大的子集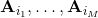。 4. 用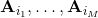重新擬合先驗分布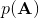。 我們擬合的分布通常使用多元高斯分布，在維度較高時甚至簡化成協方差矩陣為對角陣的情況也不錯。有一種叫做 CMA-ES 的方法，有點像是在 CEM 方法中加入動量以進行改進，每次不是重新去擬合高斯分布，而是去追隨一個高斯分布跟隨 J 值最大子集移動的方向。這類優化方法本質上并不是很好，只是因為做起來比較容易：如果都是使用神經網絡的話，這些值求起來比較容易，也比較適合并行。所以這個方法的優點主要是，一，非常簡單；二，并行求解起來非常快。但是它也有很嚴重的問題，第一點就是這種基于抽樣的方法對維度有比較強的限制，即便我們的問題不是很病態，維度一大也會很容易錯過表現好的抽樣區域；第二點我們這樣抽樣也使得我們只能處理開環規劃的問題。 ## 蒙特卡洛樹搜索 (MCTS) 在離散決策問題中，**蒙特卡洛樹搜索** (Monte Carlo Tree Search, MCTS) 是用于求解閉環控制的復雜問題的更先進的工具。這一方法在離散問題中非常通用，它也在 AlphaGo 的早期版本中承擔很重要的作用。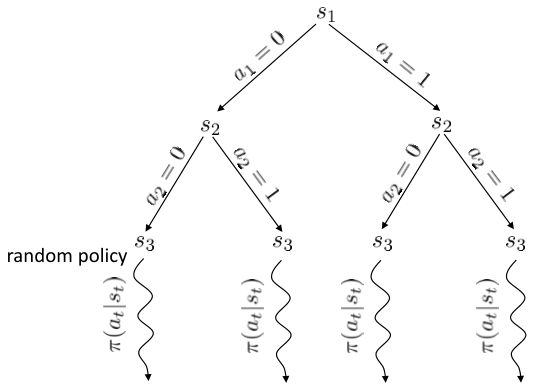  在上圖中，我們假設初始狀態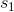已知，每一步的行動有 0 和 1 兩種。每次執行完畢一個操作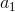以后，就會進入一個新的狀態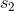，然后繼續往復。這樣我們隨著時間展開成一棵非常龐大的樹，要想去對這棵樹做一個徹底的搜索（哪怕展開的層數一多）顯然是非常不切實際的。在之前我們采用了“樹搜索”的思想，這個時候我們對其加一些“蒙特卡洛”。我們搜索到一定程度后，樹就不再展開：把此時的葉子節點作為葉子來看待，使用一些啟發式策略（也可以是隨機策略）來評估這些葉子節點的好壞。即便這個策略并不好也沒關系，我們只需要繼續對每個葉子節點出發繼續執行這個策略若干步來看最后結果怎樣，來大概給這個葉子節點的效果打個分。注意，此時打分的復雜度不再是指數級別的，而是**葉子的個數**乘上**啟發式策略運行長度**。這個方法的基本思想是，如果當前已經進入了一個優勢很大的局面（或者已經贏了），那么一些比較菜的策略也應該能把優勢保持到最后；如果我們已經進入了一個怎樣都會輸的不利局面，那很多人的選擇也是亂玩把游戲結束了。因此不會對我們的啟發式策略要求很高。因此，在實際中，大家做 MCTS 的時候通常選擇的就是隨機策略，選一個很好的策略通常是次要的。 在實際中，即便我們對深度進行了限制，這棵搜索樹的節點擴展還是指數級別的。因此，我們不能指望搜索所有的路徑。MCTS 的最核心想法還是搜索最“有前途”的節點（**選擇最大價值的節點**），然后加入一些小小的修正，來補償那些訪問比較少的部分（**也傾向于很少被訪問到的節點**）。譬如說我們從一個節點出發走一步，行動 0 之后的節點打分為+10，行動 1 之后的節點打分為+15。當然，這些都不是這個行動真實價值：因為畢竟只是一些很糟糕的隨機策略得出的評分而已，而且可能有一定隨機性。但是這個值還是有一定意義的，可能認為+15 的節點比+10 的節點可能會稍微好上一點點：因此如果我們時間有限的話，更愿意在+15 的節點上進行探索投資。 MCTS 的一般結構為： 1. 假設當前決策的根節點為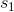，使用某種 TreePolicy(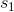)得到一個葉子節點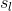。 2. 使用某種隨機策略（或其他）DefaultPolicy(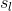)評估該葉子節點。 3. 更新在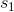到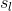路徑上的所有值，并返回第一步重新循環若干次。 4. 循環 1-3 若干次后，從根節點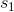的所有決策中找一個評分最高的。 TreePolicy 有很多，其中一個很流行的 UCT (Upper Confidence Bounds for Trees) TreePolicy(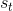)為：如果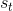沒有完全被展開（也就是從狀態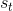有行動沒有被評估過），那么選擇一個沒有評估過的新行動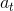；否則就選取一個得分最大的兒子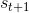，其中得分公式為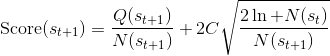，越大越好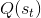，為該節點為跟的子樹的所有已經被展開過的節點的評分之和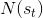，為該節點為根的子樹中已經被展開過的節點個數，因此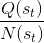就是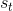的平均評分了；后者則是用來評估稀有性。我們使用一個例子來解釋該算法。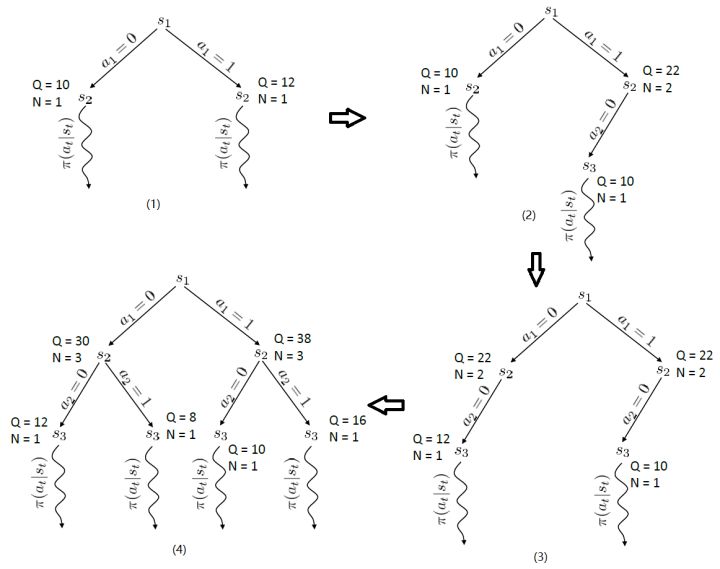  假設每個節點的行動都是 2 個。在一開始，我們只有一個節點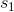，沒有被展開，根據 UCT TreePolicy(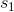)策略，我們應該展開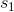的所有行動，得到新節點后進行評分。我們經過某種隨機策略得到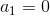下的新狀態評分為 10，因此 Q 值和 N 值分別更新為 10 和 1；同樣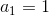下的新狀態評分為 12，由此得到圖(1)。此時，節點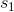的所有行動都已經完全展開，因為兩棵子樹展開程度一致，通過 Q/N 的比值，我們決定展開右側子樹一步，得到(2)中的節點，根據隨機策略評估得分為 10。此時右側的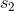的 Q/N 比值為 11，仍高于左側，但是差距不大，我們假設得分公式中第二項左側明顯占優勢（因為右側已經訪問過了，左側還沒訪問過），此時左側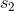得到展開，得到圖(3)，接著繼續迭代兩次得到圖(4)。 關于 MCTS，Browne et al. (2012)的"A Survey of Monte Carlo Tree Search Methods"給了一個很好的研究綜述。Guo et al. (2014) 發表在 NIPS 上的"Deep Learning for Real-Time Atari Game Play Using Offline Monte-Carlo Tree Search Planning"一文提供了一種使用 MCTS 來提供 Atari 游戲樣本，并使用監督學習（也就是之前所提到過的[模仿學習](https://zhuanlan.zhihu.com/p/32575824)）的方法來訓練 Atari 游戲策略。他們使用 DAgger 算法來實現模仿學習，回憶 DAgger 算法的第一步是從數據集訓練策略，第二步是用策略取得新樣本，第三步是**人工標注新樣本**，第四步是將新樣本并入數據集。他們在第三步中引入 MCTS 來對每個樣本進行“應該選擇哪個動作”的標注。之所以要在 MCTS 之外訓練一個游戲策略，一方面是因為在實時游戲中，MCTS 通常效率很低，而且耗費很大計算量（_ 注：這也是 AlphaGo Lee 版使用大量計算力，每一盤據說耗費電費數千美元的原因，而進入 AlphaGo Master 版認為神經網絡已經效果不錯了，那么 MCTS 的地位就下降了，決策更加輕量級：MCTS 的引入是為了彌補神經網絡不準確的缺陷 _）；另一方面，訓練一個策略可能會有很多其他用途，比如做一些感知 (perception) 和泛化 (generalization) 到其他狀態。 ## 軌跡優化 **軌跡優化** (Trajectory Optimization) 是連續控制中的重要問題。在這里，我們假設狀態和行動都是連續的。使用控制的記號，我們的問題可以被寫作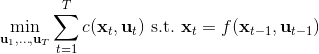：，其中 x 代表狀態 s，u 代表行動 a，f 代表狀態轉移（動態，dynamics）。在這里，因為約束是等號，對于這樣的確定性問題，我們也可以寫作一個無約束問題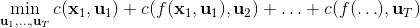：，由于非常復雜通常不會這么去寫，但是這么寫是無約束的所以一定程度上更方便使用一些基于梯度的優化算法。我們需要的是以下幾類梯度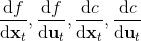：，使用類似于反向傳播的鏈式法則，我們就能求出目標函數關于行動的梯度。 在實踐中，這樣的一階算法通常效果并不是很好，使用二階微分信息通常是非常有幫助的：原因是，考慮到第一次行動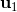，在整個式子里面出現了很多次，因此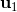的值是非常敏感的，相對來說最后一次行動的影響則非常小，這樣得到的梯度是非常病態 (ill-condition) 的，容易梯度爆炸或者梯度消失。因此使用一階算法在實踐中往往不太可行，但是好消息是這樣的問題結構事實上容易得到一些非常有效的二階算法。注意這些算法并不去訓練一個神經網絡，但對解決這一類的或者相關的增強學習問題很有幫助。  關于軌跡優化，有兩類思想有所區別的算法（_ 注：我不知道這兩個名詞應該怎么翻譯，就隨便寫一個意譯了 _）。一類是**射擊法** (shooting method)，這類方法只關注去優化每一個時刻的行動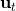，而把狀態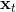看作是行動產生的結果。本質上就是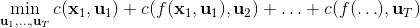，之所以叫做射擊法是因為如上圖，動作稍稍一晃就會打出差別很大的軌跡來。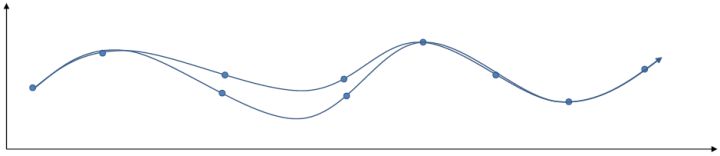  另一類叫做**搭配法** (collocation method)，同時優化每個時刻的狀態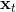和行動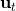，同時使用約束來將狀態和行動維系起來（甚至有時候只優化狀態，而把行動看成狀態轉移的手段）。本質上就是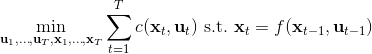。搭配法有點像上圖，一條軌跡上由很多釘子確定，然后可以通過移動釘子來改變這條軌跡。它相對射擊法來說更加穩定，但是問題更難求解（需要引入約束條件）；如果我們不想引入約束，那么就會遇到如射擊法一樣稍微一晃差異很大的問題。 在為非線性動態系統提供求解方法之前，我們先來研究一類線性模型，以及對應的控制器 LQR (Linear Quadratic Regulator, 線性二次型調節器)。它研究的問題是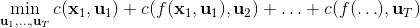中，動態系統為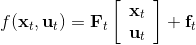的線性形式，這一類線性系統非常有局限性，但同時也特別好求解；代價函數為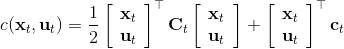的二次形式（我們在優化問題中就不關心常數項了），因此叫線性二次型調節器。這一類問題可以在一定程度上泛化到非線性模型，因此我們先來研究如何求解這個問題。 LQR 的主要想法依然是類似于動態規劃的逆推算法。首先，我們先從遞推邊界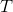階段開始研究。假設我們現在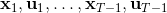都已經確定了，先當它們是常數進行處理，那么我們的目標函數僅剩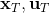，可以寫作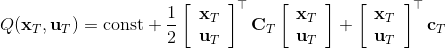 （Q 函數在這里是未來代價，cost-to-go，之前我們出現過未來收益 reward-to-go），其中，以及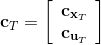。該函數的一階最優化條件是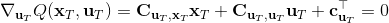（這里假設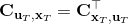了，不然需要稍微變化下）。這樣，假設矩陣可逆，我們在最后一個階段的最優決策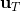就可以寫成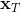的函數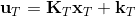：，其中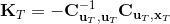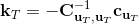，。這某種意義上可以看作是最后一個階段的策略函數：給定狀態，最優決策是狀態的線性函數。如此，我們就能用最后一個階段的狀態完全確定最后一個階段的最優決策了，使用代入消元法，我們得到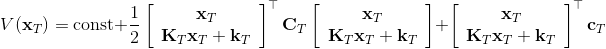 。將其展開后進行一些整理，我們得到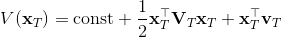，其中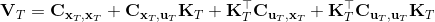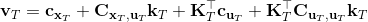，。 現在讓我們倒退到倒數第二個階段，研究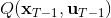。其表達式為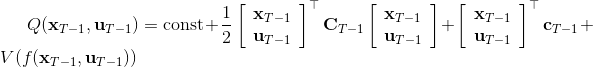注意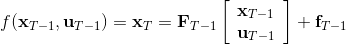。里面的 V 函數我們在前面已經確定了是一個關于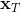的二次型，而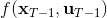是一個線性函數，因此 V 關于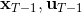是二次的，經整理后得到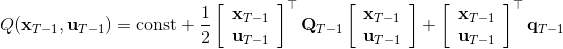，其中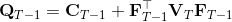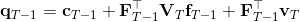，。根據一階最優性條件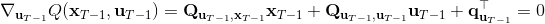，最優決策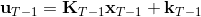，其中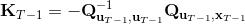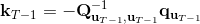，。然后繼續得到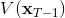，以此類推。因此，LQR 中，我們為了求出最優決策，通常會執行以下過程： for 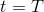 to 1: 1. 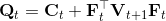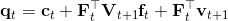， 2. 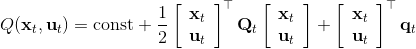，因此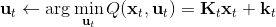，其中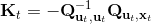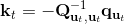，。 3. 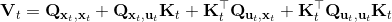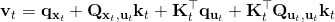，，從而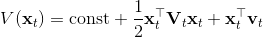。 其中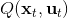，代表了我們從狀態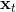執行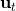后直到最后的最小代價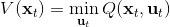，是從狀態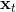出發直到最后的最小代價，有點像之前的 Q 函數和值函數的關系。求解完后，如果我們知道初始狀態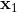，就可以在每一步執行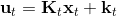作為最優策略。 LQR 在隨機系統中也能起到一定作用。在某些高斯隨機過程中，如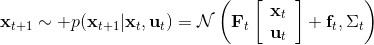，相當于是在原來的確定性過程中加入了一些（單峰）高斯噪音，噪音協方差陣可以是時變的，這個在建模中還是比較普遍的。這樣的系統中最優解依然是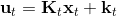，也就是說在這個問題中，我們可以忽略高斯噪音的影響。其原因主要是高斯分布具有對稱性（解析地看，高斯隨機變量的二次型的期望有解析解）。但是，如果噪音和狀態、行動有關，那么問題就變得非常復雜了。 現在我們將 LQR 算法應用到非線性問題中去。對于可微的非線性問題，為了利用 LQR，我們期望它能使用某種近似手段近似到 LQR 的結構中去。一個非常直接的做法是在函數局部性上做點文章，局部進行泰勒展開進行近似，為了在形式上保持一致，我們將動態函數 f 展開到一階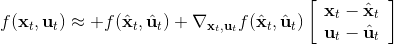：，把代價函數 c 展開到二階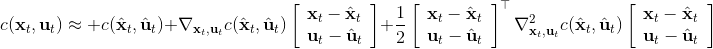： 。從而，在每個展開點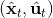，我們以它為原點建立坐標系，令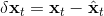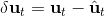，，定義新的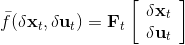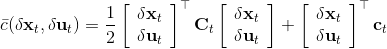，，其中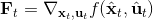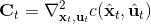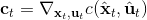，，。這樣我們就可以用這么一套新東西來運行 LQR 了。這個方法叫做迭代 LQR (iterative LQR, iLQR)，一個簡單版本迭代執行以下步驟直到收斂： 1. ，，。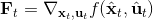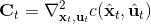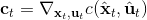 2. 使用 LQR 逆推得到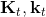，其中每一步代入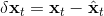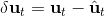，。 3. 根據上一步的結果，順推得到所有的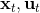，其中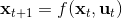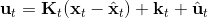，。 4. 使用第三步的結果更新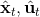。 這個方法事實上是一種近似的牛頓法來求解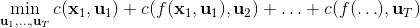。牛頓法求解的過程也是每一步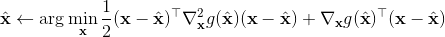，而 iLQR 的想法也跟牛頓法一樣，局部近似一個復雜的非線性函數。但是 iLQR 并不等價于牛頓法，而確切使用牛頓法需要將動態系統 f 展開到二階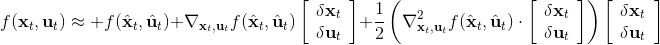：，這樣的方法也被稱為**差分動態規劃** (Differential Dynamic Programming, DDP)。在實際中我們通常不這樣使用，因為 f 通常是一個向量值函數，做二階微分以后會變成一個張量，會比較復雜。在實踐中，一階微分就效果不錯了，雖然它需要更多步數才能收斂，但是考慮到計算二階微分的成本，還是值得的（iLQR 只是 DDP 方法去掉了 f 的二階微分）。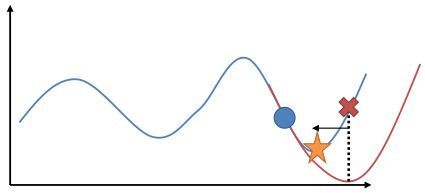  在使用牛頓法來求解非常復雜的非線性函數時也有一些技巧。如，如果我們每一步都執行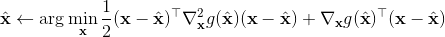，不見得是好的。這是因為梯度和 Hessian 陣都是局部的，而實際函數并不是一個二次函數。如實際函數是藍色曲線，在藍色點上近似展開到二階，便“認為”該函數是紅色的二次函數，然后嘗試去找這個函數的最低點。然而，這個解可能在實際中并不好（在紅叉位置，走得太遠了），甚至比原來的解更大了，實際最優解在五角星位置。所以一個比較好的處理方法是做一些線搜索 (line search)，也就是把 iLQR 的第三步中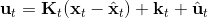，改為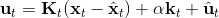，其中是一個較小的系數。注意如果是 0，那么在迭代中軌跡不會發生變化。因此決定了如何關于舊軌跡和新軌跡的插值比例系數。一個比較簡單的方法是搜索，直到它提高了預期設定的一個比例。關于這塊文獻，Mayne and Jacobson (1970) 最早提出了 DDP 算法，Tassa et al. (2012) 給出了做 iLQR 的實踐指導意見，Levine and Abbeel (2014) 給出了不用線搜索的另一種信賴域方法。 Tassa et al. (2012) 使用 iLQR 做模型預測控制 (Model-Predictive Control) 來控制模擬機器人。這并不是與深度增強學習緊密相關的，只是使用了 iLQR 方法。他們的控制架構是在每一步中， 1. 觀察狀態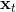； 2. 使用 iLQR 來計劃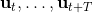，來最小化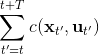； 3. 執行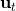，拋棄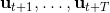。 也就是說，在每一步中先使用 iLQR 對未來若干步進行計劃，然后只采用第一步的策略，然后下一次重新進行多步規劃。本質上它不是一個“學習”過程，所有執行內容都是在線計劃的，因此能夠非常好地抗新加入的外力干擾（如何在外力干擾下讓機器人保持直立，如何在模型錯誤也就是質量錯誤的情況下還能保持直立），穩定性非常好。（_ 注：非常建議大家自己去看一下這個視頻：_[http://homes.cs.washington.edu/~todorov/media/TassaIROS12.mp4](https://link.zhihu.com/?target=http%3A//homes.cs.washington.edu/%7Etodorov/media/TassaIROS12.mp4)）這個主要意義是，如果我們能有模型的話，即便我們不做學習也能夠做很多事情。 在真實問題中，我們的模型可能會很復雜，甚至很難說能寫下一組物理方程就能表示問題；和人類、互聯網互動的就更加不確定了，我們能做到最好的可能就是從數據中進行一些建模了，在接下來我們將繼續介紹基于模型的增強學習算法。