# (5) 演員-評論家算法 > 作者：[謝天](https://www.zhihu.com/people/xie-tian-55-77) > > 來源：[POST 館](https://zhuanlan.zhihu.com/c_150977189) ## 策略梯度法與值函數的結合 在上一篇中，我們已經了解策略梯度法的本質是找出目標函數對策略的梯度的一個估計量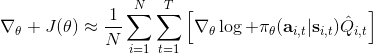，其中**今后收益** (reward-to-go)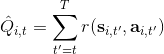，然后將策略沿著這個梯度方向走一步。注意到使用今后收益是由**因果關系** (casuality) 所得到的。 讓我們把視線聚集在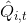，注意到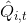其實是在狀態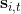下選取行動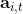之后的期望收益的估計量。這里使用字母 Q 絕不是偶然的，因為我們顯然已經發現了它與我們在[第三講](https://zhuanlan.zhihu.com/p/32598322)中所提到的 Q 函數有非常密切的關系。如果我們要得到其估計量，可以求出我們模擬出來的一條軌跡的收益的后面一段也就是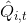。但是事實上我們在之前也說過，在同一個分布中抽取的軌跡可能也是千差萬別的。用 MDP 的語言解釋，可能是因為我們在之后根據策略函數分布隨機選擇了不同的動作，也有可能是選擇了同一個動作但是由于系統環境的隨機性導致下一個狀態不同。一句題外話是，自從高三暑假拿到復旦本科錄取通知書，上面有一句話我一直都很欣賞，“_ 一個真實的現在可以開墾一萬個美麗的未來 _”，大抵如此：從一個起點出發的軌跡從來都不見得是殊途同歸的，也很難用一個學生的人生去衡量整個學校的學生。 結果就是，真實的期望收益遠遠比根據策略做出行動的與系統互動的結果要復雜，無數的未來情況需要被平均在一起去得到真實的今后收益，本質上是一個積分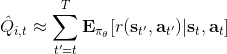：。也就是說，真正的期望今后收益應該是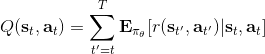。一旦我們知道期望今后收益，那么我們可以用它來替代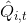，即如果我們能用某種方式得到 Q 函數的值，那么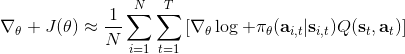將會成為一個更好的估計量。當然我們可以說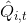是一個無偏估計，但這個估計其實只用了僅僅一個樣本，會導致估計的方差非常大；如果你有無限個樣本，那么方差就會比較低了。如果我們能把真實的 Q 函數值代入進去的話，那么我們就可以期望策略梯度有一個較低的方差。這也正好是我們在上一篇中提到的策略梯度法的最大瓶頸之一是高方差，解決這一瓶頸問題，我們就傾向于認為可以收斂到一個更好的解，或者使用較大的學習率（也就是增加單步步長），從而收斂得更快。 同樣，我們可以引入基準線技術。我們選擇的一個比較好的基準線是同樣在第三講中出現的值函數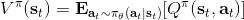，也就是在給定策略下 Q 函數的期望。之所以采用值函數，是因為這和我們在[上一篇](https://zhuanlan.zhihu.com/p/32652178)中所提到的平均情況不謀而合：之前認為一個不錯的基準線是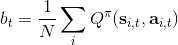，而這里也正好是對應的期望。此時我們的估計量就變成了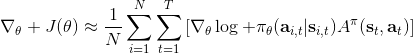，其中 > **優勢函數** (advantage function) 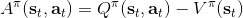，表現了給定策略，在狀態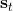下，采用了行動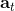能比該策略的平均情況期望今后收益多出多少。 根據定義，如果我們對優勢函數關于行動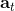取期望，結果是 0。這樣的“杠桿”也正是我們想要的，使得更好的行動可能性更大，而規避更差的行動。同樣的，如果我們能對優勢函數估計得越好，那么策略梯度的方差就可以越小。回顧我們之前的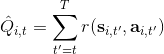是一個無偏估計，但是它的方差相當大；而我們考慮要做的是犧牲一點點無偏性，引入一個神經網絡（神經網絡總不是完美的），但期望它能顯著地降低方差。這個偏差-方差的權衡在統計中是非常常見的。 ## 演員-評論家算法 回到我們的一般步驟中，我們來看它與策略梯度法在第一步生成樣本和第三步策略改進上并沒有顯著區別，主要區別在于第二步：我們現在嘗試去做的是去擬合一個值函數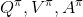：三者之一，以期能得到一個更好的梯度估計。我們真正從“估計收益”變為了“擬合模型”。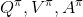 三者都是緊密相關的，那么我們到底去擬合哪個呢？一個非常自然的想法是去擬合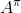，因為這是我們在梯度表達式中直接要用到的東西。我們可以生成一些數據，然后使用監督學習方法。這里有一個小技巧：我們發現 Q 函數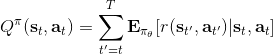取決于狀態和行動兩個維度，因此輸入是對應兩個空間的笛卡爾積。但是維度越大，同樣的樣本數估計的方差越大。根據 Q 函數和值函數的關系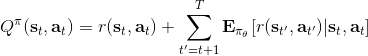， ，因為在我們的問題結構中，給定當期的狀態和行動，當期的收益就是確定的了，可以把當期的收益提出來。而后邊那塊求和項其實就是值函數的期望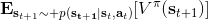。如果我們愿意做一點近似，用軌跡樣本來估計這個期望——此時不是使用整條軌跡，而僅僅是看一步以后的狀態，那么我們的 Q 函數可以近似為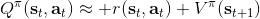。與此同時，優勢函數也可以被近似為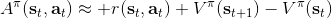。這么一來，其實我們只要去擬合值函數 V 就好，其他的都可以被近似表示，這樣擬合神經網絡的維度的輸入空間就只需要是狀態空間了：要做的事情是去訓練一個神經網絡的參數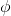，使得輸入為狀態，輸出給定策略下值函數的估計量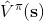。因為實用性和便利性，絕大多數的演員-評論家算法都是去**擬合值函數 V**。 給定一個策略去擬合這樣一個神經網絡的過程我們稱為**策略評估** (Policy Evaluation)。這個步驟不嘗試去改進策略，它只是想從任意給定的狀態出發，評估這個策略有多好。由于值函數表達式為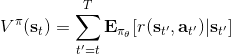，目標函數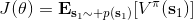只是值函數的一個期望而已，所以擬合值函數 V 同時也為我們帶來了目標函數。那么具體怎么做策略評估呢？與策略梯度法相似，我們依然使用蒙特卡洛方法，進行一次軌跡采樣以后來近似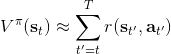；當然如果我們可以重啟模擬器的話，最好能做多次軌跡采樣后得到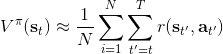，但是前者其實也還是不錯的。 神經網絡會有一些偏倚。因為可能我們從比較接近的兩個狀態出發做出的兩條軌跡，結果上可能會有很大的偏倚；而對于神經網絡來說，相似的輸入基本上也就對應了相似的輸出。畢竟神經網絡只是一個函數的逼近器而已，對于確定性模型，它的輸出是良定的 (well-defined)，意味著對于同一個輸入對應同一個輸出。神經網絡擬合很多樣本，將其綜合起來得到一個低方差的估計：從相似的出發點，一條軌跡極好，另一條極不好，神經網絡會認為這是不合理的，并將其平均處理。如果樣本越多，函數將近似得越好，結果就越好。但是譬如在兩個相似狀態之間存在一個斷崖，那么答案就會出現問題，但是不管怎么說估計的方差總是小的。 訓練神經網絡的方式非常傳統，就是收集一些訓練數據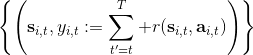，然后最小化諸如最小二乘的損失函數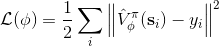。這是一個非常通常的損失函數，在最優控制中這個損失函數有一些概率解釋；當然也可以用 Huber 損失函數，效果也是很好的。我們嘗試去將其做得更好，意思是進一步降低方差。注意到在理想化的完美情況下，我們的目標是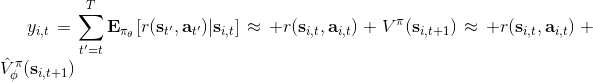。第一個約等號和前面 Q 函數時候的技巧一致，用一步軌跡做近似；第二個約等號是將值函數 V 用神經網絡做近似。這某種意義是一個自助方法 (bootstrap)，如果神經網絡相對于直接將軌跡的后半段加和的效果更好，那么就應該這樣做；雖然這樣近似使得估計有偏，但是我們期待函數估計的方差更小。看起來好像這樣訓練神經網絡就是從里面拿出數據再放回去，其實不然，我們給它加入了些許知識，降低了其方差。進一步將這個一步估計泛化，我們可以做兩步、甚至多步的估計，本質上是兩者的折中版本。Levine 教授也提到了，訓練神經網絡的初值會影響訓練行為，如 Q 學習中設置一部分初始的值函數非常大，來使得初始的更希望去試探這塊區域。在演員評論家算法中，初值通常設置得比較小，這是為穩定性著想。 策略評估的兩個游戲相關例子。Tesauro (1992) 使用增強學習在西洋雙陸棋上取得了成功，做了一個 TD-Gammon 軟件：當然事實上它只是一個值函數方法而不是演員-評論家算法。它的收益函數是游戲結果，值函數是給定局面狀態，輸出期望游戲結果。Silver et al. (2016) 給出了舉世聞名的 AlphaGo，使用了蒙特卡洛樹搜索 (MCTS)、值函數擬合和策略梯度等方法，事實上收益函數和值函數的想法和前者還是接近的，不過用了一些卷積神經網絡。在這些例子中，策略評估的解釋是相當直觀的。 這里給出一個比較簡單的演員-評論家算法，稱為**批量演員-評論家算法** (batch actor-critic algorithm)，與策略梯度法的結構非常相近： 1. 運行機器人，根據策略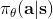得到一些樣本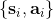，包括所處狀態、行動和收益。 2. 使用樣本收益之和擬合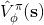。這一步樣本可以做蒙特卡洛，也可以做自助法；擬合可以用最小二乘的目標函數。 3. 評估優勢函數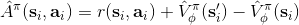。 4. 放入策略梯度函數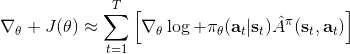。 5. 走一個梯度步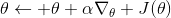。 ## 貼現因子 如果說機器人拼樂高的問題是有終點的 (episodic)，而訓練小人行走，我們通常希望它能一直走下去 (continuous / cyclical)。這種無限期的問題會使得目標函數值越來越大。在上面我們使用了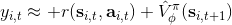作為估計，然后用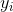去訓練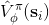。那么對于無限期的問題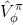，可能會在訓練中逐漸增加（減少），在很多例子中都能達到無窮，這樣的情況就很麻煩了。為了解決這個問題，接下來我們要引入**貼現因子** (discount factor) 的概念，這個概念在金融、經濟等領域相當常見：一般認為一筆錢在眼前的價值會比未來的價值要高，也可以與金錢的通貨膨脹聯系起來。因此，在建立模型時，我們也希望收益發生時間更接近眼前。我們的方法是，加入一個小小的貼現因子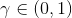，然后修改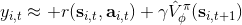。在實際應用中貼現因子設置成 0.99 效果不錯。 實際上，引入了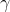并不影響整個 MDP 框架，只是稍許改變了轉移概率函數。我們可以將這個貼現因子放進 MDP 的架構進行解釋。以離散問題為例，如原來的轉移概率為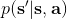，我們在狀態集合中新增一個死亡狀態 (death state)，本質上是一個吸收狀態，且此后收益一直為 0（或者理解為游戲立即結束）。我們構建新的轉移概率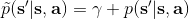，，且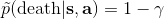。這也就是說在任意情況下，都有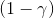的概率游戲結束，此后不收集任何收益。 拋開演員-評論家算法，現在我們討論如何將貼現因子引入到策略梯度法中，稍稍有些復雜。對于蒙特卡洛策略梯度，我們有以下兩種選項。這兩者其實都可以有演員-評論家算法版本，但首先先寫成策略梯度法形式。 第一種選擇是我們直接利用因果關系后的式子，對后半部分進行貼現得到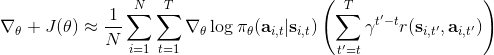，如果我們式子中加入了評論家的話就變成了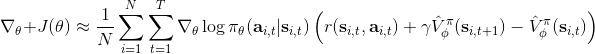；第二種選擇是我們回到一開始的策略梯度式子，進行貼現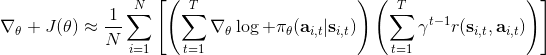。這兩者其實是不相等的，可以發現將第二種選擇進行重組后變成了 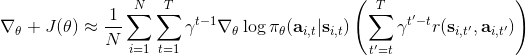 ，多出了一項對梯度進行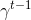貼現的系數。主要的區別是，第二種選擇的做法使得越往后的步驟影響力越小。但是看起來很奇怪，我們一開始使用正確的策略梯度法，但是如果使用第二種選擇進行貼現的話，梯度也被貼現了。事實上，如果你想從初始時間點 1 開始進行貼現，第二種選擇的表達式是正確的；但是一般來說沒人想這么做，我們一般還是采用第一種選擇。原因是，譬如我們想運行一個小機器人無限長時間，我們一般不關注它在第一個時間點是不是速度很快，而是在每一個時間點是否很快。我們采用第一種選擇，是想去**近似一個無限時間長的平均收益，且使用貼現因子**。這樣就可以對無限期問題有一個總和的界。關于這個理論是比較復雜的，可以參考 Thomas (2014) 發表在 ICML 上的文章。 現在我們把貼現因子加入到演員-評論家算法。在之前的批量演員-評論家算法中，只需要把第三步從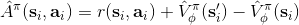變為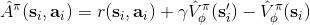就可以了。注意貼現因子使得對于無限長問題也有一個上界。我們在這里同樣給出一個**在線的演員-評論家算法** (online actor-critic algorithm)：前者與策略梯度法相似，是根據策略生成一大堆軌跡，然后做一個很大的計算更新，再重新生成策略。在線算法可以在每一步收集樣本之后，就立即更新評論家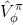和策略。 1. 在線運行機器人，根據策略執行行動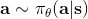，得到一個狀態轉移樣本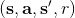，即從一個狀態出發執行某行動到哪個新的狀態，單步收益多少。 2. 使用評論家的結果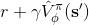來更新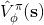。 3. 評估優勢函數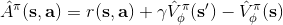。 4. 放入策略梯度函數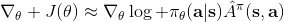。 5. 走一個梯度步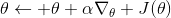。 可以發現，第二步我們只用一個例子去更新。我們這么急迫的原因是，如果我們沒有評論家，我們就不知道這個結果到底應該是什么。如果我們有了好的評論家，那么我們就可以做這樣的自助法了。第三步只需要算一個值就行了，第四步也是單樣本的梯度。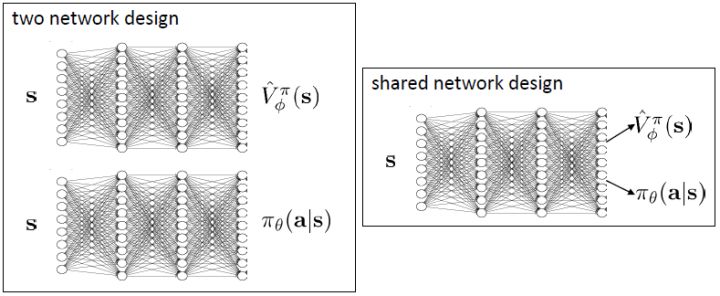 ## 實現細節 現在我們來研究批量和在線的演員-評論家算法的實現細節。首先第一點是算法中的神經網絡結構設計。相對于之前的模型我們只有一個從狀態映射到演員策略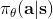的神經網絡，在這里我們還需要去近似評論家函數，因此會有一個從映射到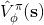的神經網絡。一個非常直觀的做法是，我們可以將兩個網絡分別訓練，成為兩個獨立的網絡。這樣做法的主要好處是簡單而穩定，也是在一開始上手的時候非常建議使用的。但是一個很大的不足是，在演員和評論家之間并沒有建立起共享的特征，譬如如果特征是非常高維的圖像，那么如果在圖像的低級別特征（也就是經過多層卷積）進行共享還是有意義的。因此一個替代的解決方案是使用同一個輸入，構建一個同時輸出演員策略和評論家函數的輸出。這在網絡特別大的時候更有效，但是缺點在于訓練起來可能會比較惡心，因為會有兩個不同的梯度（策略梯度和回歸梯度）往不同的方向推動共享的參數，數據類型也不太一樣，因此讓這個網絡穩定下來需要很多技巧，如初始化數值和學習率的選擇。Levine 教授的建議是，如果模擬器（如 Atari 模擬器和 MuJoCo）很快的話，不妨使用雙網絡結構，這樣比較容易。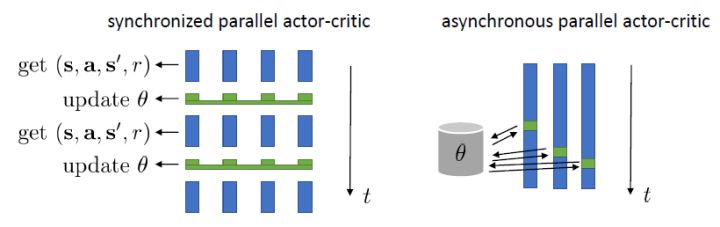  在上一節的末尾我們提到了在線演員-評論家算法，其中第四步只用一個樣本去估計梯度，第二步也只用一個樣本去更新評論家函數。這樣做多少是有點困難的，因為方差會相當高。問題主要出在它依然是一個在線 (on-policy) 算法，在線意味著在第五步更新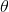之后，所有的樣本需要推倒重來。如果我們能做出一個批量的樣本，那么效果可能會明顯變好。一個方法是我們盡量少去更新策略，將這個算法弄成擬在線 (quasi-online) 的形式，做多步之后再去更新策略。如果我們可以假設樣本可以由多個智能體（多輛汽車，多個機器人等）來收集的話，一個更好的方法是并行訓練，如下圖。第一種是采用左邊圖形的**同步法** (synchronized)，多個智能體各走一步得到訓練數據，用樣本數據去計算梯度，先完成的需要等待（因此是一個同步點）；然后用多個智能體的梯度加總起來更新演員策略參數網絡，大家再去根據新網絡執行下一步。每次可以是不同的狀態，不同的行動，然后到不同的下一個狀態，但這都是不相干的：每次采樣完畢后可以繼續運行，可以重啟，也可以其他操作。一種更先進的方法是**異步法 ** (asynchronous)，基本上就是移除這些同步點，每個智能體完成操作以后就去用自己的梯度去更新中央服務器參數，中央服務器積累了一定的步數，就把更新信息發送回所有的智能體。有點像閉著眼走路，但是實際上運行得不錯。移除同步點后通常實現簡單，更快，基本上哪兒都好；但希望模擬本身要非常快。  我們進一步想看基準線方法如何更好地應用于演員-評論家方法。對于演員-評論家算法，我們的策略梯度估計為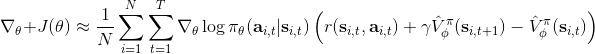。這個方法的主要優點是我們采用了評論家函數，因此希望有一個更小的方差；然而這個估計并不是無偏的，因為評論家函數總不能被完美擬合；而且在訓練的前期評論家函數通常非常不準確，因此不管方差有多小因為評論家函數的無意義導致怎么都不會得到一個很好的值。另一個極端是策略梯度法完全的蒙特卡洛抽樣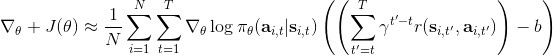，，其中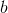是任意常數。這個做法的主要是之前我們已經證明了的無偏性，也提到了主要缺點是單樣本估計的極高方差使得本身并不怎么有意義。這邊評論家函數的另一種正確用法是，將評論家函數（根據當前狀態的）作為基準線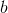，從而得到。與之前的常數不同，這個基準線是依賴于狀態的；但是這樣做依然是無偏的（類似之前的推導展開），而且事實上改為任何只與相關的函數都是無偏的。因此無偏性得到了保留，但是如果基準線接近真實收益，那么方差就會大大降低。依賴于狀態的基準線能更敏感地解決問題，比一個常數的降方差功效更好。 我們新引入了一個依賴狀態的基準線，那么我們現在想在此基礎上進一步引入行動。考慮優勢函數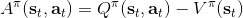。它的一種估計是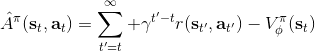，顯然它是無偏的，但是因為這是單樣本估計所以有高方差的問題；然而如果我們使用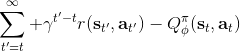來作為根據，如果評論家函數是正確的那么它的期望將達到 0 是非常好的，但是這個估計根本就不正確。那么有沒有補償方法呢？我們看這樣一個結構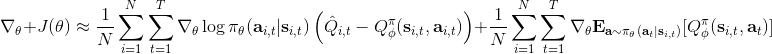：  ，雖然前面一項本身不正確，但是我們在后面加入了一個修正項使得其無偏：如果我們能用一個辦法來評估第二項（根據 Q 的結構不同，可能有一些結構可以以解析形式表達，如策略是高斯的，Q 函數是二次的，那么這個結構就是可以在沒有樣本的情況下得到評估的，但是是否有這樣的結構還是很需要運氣），這個無偏估計就可以用。這樣的用 Q 函數作為評論家的相關內容 (Q-Prop, Gu et al., 2016) 會在后續課程中更多提到。因此，我們得到的啟發是，基于狀態的基準線是無偏的，基于行動的基準線是有偏的，但是偏差有可能可以通過一個校正項補救回來。 在之前我們適用的演員-評論家算法的估計都是一步的，即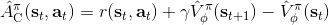。下標 C 的意思指的是評論家 Critic。這個估計的優點主要在于方差較低，但是缺點也很明顯，如果值函數是錯的的話，那么就會引起很大的偏差（當然肯定總是錯的）。另一個極端就是純粹的蒙特卡洛而不使用評論家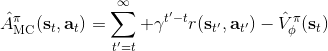，。我們也知道了它是一個無偏估計，但這樣的單樣本估計的方差非常高。現在我們考慮一個方法，中和兩者的優缺點，得到一個折中方案。一種方法是對兩者進行混合，如果發現方差或者偏差過高，那么就提高或者降低組合系數。另一個是，我們發現由于貼現因子的作用，這樣指數下降的函數，隨著時間往后推移，收益的貢獻比例將非常低。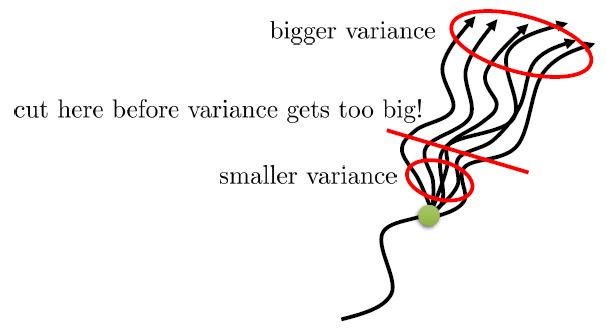   在上圖，從一個狀態出發，不同的軌跡的效果隨著時間后移而漸行漸遠，因此是一個從小方差到大方差的過程，貢獻逐漸下降而方差逐漸上升。單個樣本很容易被淹沒于未來軌跡的汪洋大海之中，遙遠的未來的可能性如此之多，如果我們看 50 年以后會怎么樣基本上是做白日夢。我們要做的是在軌跡上在方差變得太大前切一條線，因為后面的步驟可能性太多，效用實在太低；而我們用評論家函數 V 去替代后面的部分，作為一個平均情況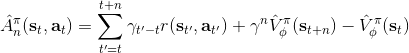：。這樣的表達式允許我們通過調整來控制偏差方差的權衡，通常選擇一個大于 1 的值如 4、5 會運行得較好。這也稱為步收益。 Schulman et al. (2016) 提出了**廣義優勢估計** (Generalized Advantage Estimation, GAE)。本質上是步收益的推廣。這種方法不再選擇一個單一的步數，而是對所有的步數進行一個加權平均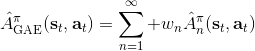，。其中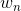是權重。現在的一個重要問題是如何選擇權重。我們希望降低方差，因此一種比較合理的方法是讓權重也指數下降，即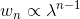，其中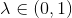 是一個底數參數，權重加和為 1。代入之后經過整理，我們可以得到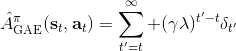，其中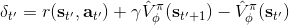是一個類似演員-評論家的東西。這個方法說明了貼現因子在里面扮演的新角色，和之前非常不同。非常像一個貼現因子，如果它比較小，那么我們將在很早期就切斷，偏差較大方差較小；反之則較后切斷，偏差較小方差較大。因此從另一種意義上解讀，貼現因子意味著方差降低。 演員-評論家算法也有很多應用。在前面提到的 Schulman et al. (2016) 使用 GAE 估計量來進行模擬機器人的訓練，用的是批量演員-評論家算法（因為模擬器中樣本容易獲取）。Mnih et al. (2016) 使用在線演員-評論家算法訓練三維迷宮導航問題，采用了異步并行的技術，使用了 4 步收益，它的演員策略網絡和評論家策略建立在同一個神經網絡之內（因為輸入是像素圖像）。