# (6) 基于值函數的方法 > 作者：[謝天](https://www.zhihu.com/people/xie-tian-55-77) > > 來源：[POST 館](https://zhuanlan.zhihu.com/c_150977189) ## 動態規劃與值函數的擬合 在上一講的演員-評論家算法中，本質上我們已經把在某種策略下的值函數（這里的值函數是廣義的，包括 V、Q、A 等）用到增強學習的算法里面去了，形成一個策略-值函數的交融算法。而在這一篇中，我們嘗試去構造一個沒有“演員”的“評論家”，也就是純粹的值函數方法。我們在之前的學習中也了解到值函數的厲害之處，它自身包含了非常多的信息。 我們在之前的兩篇中分別介紹了策略梯度法和演員-評論家算法，它們的特點本質上都是尋找策略梯度，而只是演員-評論家算法使用某種值函數來試圖給出策略梯度的更好估計。然而策略梯度通常有非常高的方差，要把它弄好需要花費很大的努力。那么我們可能會考慮一個問題：**強化學習能否徹底拋開策略梯度這一架構？** 回憶優勢函數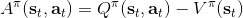，指的是給定策略，在狀態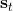下，采用了行動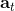能比該策略的平均情況期望今后收益多出多少。我們在演員-評論家算法里面花了很大力氣去估計這個東西。假設我們在某個策略下已經知道這個函數，那么意義是，如果我們在狀態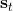下執行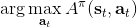，也就是根據優勢函數得到一個當前最好的決策（當然我們得堅持之后還是完全按照策略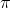來），那么根據定義，這個決策必然是在期望意義下最優的：換句話說，它至少不差于任何的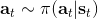。這個結論是非常顯然的；值得注意的是，這個結論的成立性是廣泛的，和策略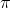具體是什么東西沒關系。 剛才的結論給了我們一個策略改進（第三步藍色方塊）的思路。對于一個策略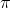，如果我們已經得到了它對應的優勢函數，那么我們必然可以構造出一個新的策略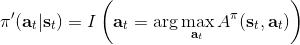：剛才我們已經指出了在任意一個狀態下，這樣的策略不差于原策略，至少和原策略一樣優且有可能更好。需要注意的是這是一個確定性策略。事實上這是本篇中要涉及的算法的內在思想。 作為開始，我們先不引入神經網絡和復雜的動態系統等很復雜的東西，假設狀態和行動的個數很少，以至于 V、Q、A 函數都能用一個表格來記錄下來；轉移概率也是完全已知的。在這個最簡單的環境里，上述算法就可以用一個非常經典的**策略迭代法** (Policy Iteration, PI) 來簡單實現。策略迭代法循環執行以下兩個步驟： 1. 策略評估 (Policy Evaluation)：計算所有的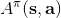。 2. 策略改進 (Policy Improvement)：令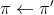，其中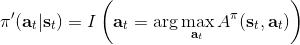。 要執行這個過程，最大的問題就是如何計算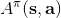。在之前我們提到的是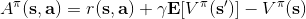，。因為在這里我們的轉移概率已經知道了，因此我們只需要去研究值函數 V 就行了。這一類方法廣義上被稱為**動態規劃** (Dynamic Programming, DP)。形式上，假設我們已知轉移概率為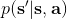，且狀態和行動都是離散的而且空間足夠小，這樣我們所有的數據都可以在表里記下來。類似于我們在之前提到的自助法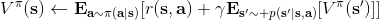，。自助法的意思是，我們只需要在后面插入當前的估計（就是查表得到）就行了。（_ 這里我補充一下，從深層次來說，這樣的表達式又叫 Bellman 方程，但在這個課中似乎不涉及到這一塊的理論 _）由于我們現在采用的是一個確定性策略，這樣的單點確定性策略也可以寫作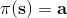，即給定狀態下得出行動這樣的一個函數形式。于是，之前的公式就可以被進一步簡寫為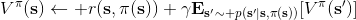——這也就成為了我們策略評估步的公式，我們用值函數 V 去替代優勢函數 A。需要注意的是，標準的策略迭代法的第一步需要關于我們的當前策略解出比較精確的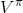，本質上是一個不動點問題：一種方法是之前的公式進行反復迭代直到收斂；另一種方法是求解一個比較大的線性系統（之前的公式是線性的）。 不要忘記我們本篇的目標是在算法中完全拋開策略函數。可以回顧我們每一步更新的新策略其實都是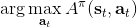，而給定狀態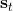下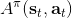，和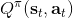之間其實只相差了一個常數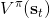，因此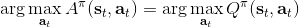，我們可以用 Q 去替代 A 在這里的地位。事實上，如果我們有了一個大 Q 表，每一行代表一個狀態，每一列代表一個行動，那么我們只需要標出每一行的最大值的格子位置就可以了，因此 Q 函數本身就可以隱式地表示一個策略；同樣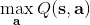，正是對應的值函數。那么這樣，我們就正式地把策略的重要地位給架空了，得到一個更簡單的動態規劃求解方法：**值函數迭代法** (Value Iteration, VI)。事實上該方法可以把以下兩步混在一起把 Q 函數架空，但是 Q 函數在我們的值函數方法中有很高的地位，我們不這樣做。我們反復執行以下兩步，直到收斂。其中第一步屬于綠色方塊，第二步屬于藍色方塊。 1. 更新 Q 函數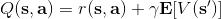：。 2. 更新 V 函數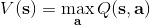：。 在對經典的兩大動態規劃算法進行完簡單的介紹后，我們考慮的是如何把這樣的方法搬運到深度增強學習中來。在相對比較復雜的問題中，我們知道狀態個數是非常之大的，很難用一個很大的表來保存所有狀態的 V 值或者 Q 值。譬如在一個彩色的賽車游戲中，分辨率是 200 * 200，那么根據屏幕顯示而設定的狀態總數可以達到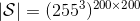，這個數字大得超乎想象。這樣的個數隨著維度的增長而幾何爆炸的問題通常稱為維度災難 (curse of dimensionality)。引入到深度增強學習中，一個非常直接的想法就是使用一個巨大的神經網絡來代替這個大表，如弄一個參數為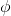的深度神經網絡來擬合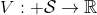函數，輸入狀態，輸出對應的值函數。為了訓練這樣的函數，我們使用一個平方損失函數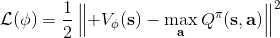來做這樣的回歸問題。從而，之前的值函數迭代法可以被改寫為以下的**擬合值函數迭代算法** (Fitted Value Iteration)： 1. 。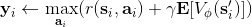 2. 。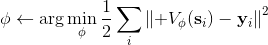 第一步我們就和之前演員-評論家算法一樣計算出一個目標，然后第二步訓練神經網絡減少神經網絡輸出與目標的值函數之間的差異。然而事實上，第一步的這個 max 操作是非常難做的：一個最大的問題是我們**假設我們已經知道了系統的轉移概率**！要做這個 max，我們必須知道每個行動會導致概率往哪些狀態轉移。我們用一些無模型的增強學習，可能可以執行很多操作來看結果，但狀態往往不能回撤復原以嘗試其他的選項；而第一步的 max 要求我們嘗試各種不同的操作來看結果。 我們嘗試去避免做這么強的假設。回顧我們之前的策略迭代法，我們迭代進行兩步：第一步求解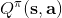，第二步用這個 Q 函數來更新策略。其中，第一步的做法可以是反復迭代值函數 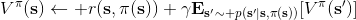 ，然后再通過一步轉移和加上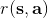 來得到 Q 函數；但同樣也可以是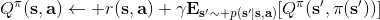。現在的 Q 函數可以用樣本來擬合出來。這一切告訴我們：只要有 Q 函數，一切就可以在不知道系統轉移概率的情況下運轉起來。進一步，我們也考慮將 Q 函數使用諸如神經網絡的結構來近似，得到**擬合 Q 函數迭代算法** (Fitted Q-Iteration)： 1. 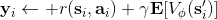，其中我們使用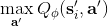來近似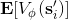。 2. 。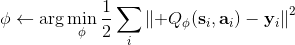 可以發現，這樣的決策算法的根本好處在于不需要去同一狀態嘗試不同的行動選項，因為 Q 函數已經告訴你不同行動的效果了：我們無需在真實環境中嘗試各種不同行動后復位，而只需要在我們所涉及的 Q 函數擬合器上做這點就可以了。此外，我們這樣的兩步算法有很大的優點。第一，算法中只需要用到很多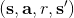的一步轉移樣本，而這些樣本是可以離線的；這個在演員-評論家算法中是不通用的。第二，這個算法只用到一個網絡，沒有用到策略梯度，因此也沒有高方差的問題。但是，這個算法的致命缺點是，對于這樣的非線性函數擬合機制下的算法，沒有任何收斂性保證（不進行擬合的大表格 Q 迭代算法在一定條件下有收斂性）。我們接下來會進一步探討這些優缺點。一個完整的擬合 Q 函數迭代算法的一個簡單框架是這樣的： 1. 執行某個策略，收集容量為的數據集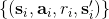。 2. 。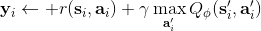 3. 。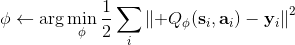反復執行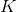次 2-3 步驟后跳回第一步繼續收集數據。 第一步的策略其實是任意的，因為 Q 函數迭代算法不對數據集的策略做出任何假設。根據收集數據數量的不同，可以變成收集一堆數據的批量算法，也可以變成只收集一個數據的在線算法。第三步可以選擇怎么去訓練神經網絡，比如走多少個梯度步，算得精確一點還是簡單走幾步就停了。 現在來解釋該算法的**離線** (off-policy) 性質。實際上第一步可以用上任意策略的數據，因為第二步和第三步的計算沒有需要用到當前策略下的數據，而只是單步轉移的片段就可以了。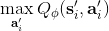只需要對決策空間的一個枚舉，而轉移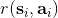，在給定了狀態和行動的情況下，也跟當前策略沒關系。某種意義上可以說 Q 函數是對策略的一個解耦合。因此，我們可以收集一大堆轉移數據放進一個大桶里，我們的算法從大桶中抽取數據，這個算法照樣可以運轉。 那么擬合 Q 函數迭代算法到底在優化一些什么呢？在第二步中，如果我們是表格 Q 函數迭代的話，max 就是在改進策略。第三步中，我們在最小化一個期望誤差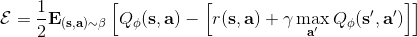，也被稱為 Bellman 誤差。可以發現，在理想情況下，如果這個誤差為 0，那么我們所求得的 Q 函數就滿足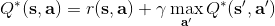，這正是確定**最優 Q 函數**的 Bellman 方程，也對應了**最優策略**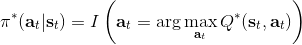：，這個最優策略最大化期望收益。如果我們不使用近似，且每一個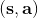都有概率發生的話，那么我們可以說明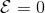對應著最優策略。在這邊，**即便算法是離線的，但是收集數據的分布還是有很大關系的**。一個極端情況，我們假設只是一個單點分布，除了一個狀態外概率都為 0：這樣我們就成為只知道一個狀態的井底之蛙了，不能對其他狀態的好壞做出正確評價。因此，盡管算法是離線的，但請盡可能確保我們收集的數據中包含了真正運行時會訪問到的那些狀態和行動。此外，如果我們使用諸如神經網絡的東西去擬合 Q 函數表，那么之前所說的大量理論保證將喪失。 在之前的擬合 Q 函數迭代算法中，我們收集大量數據，然后反復做樣本-做回歸。我們把每次收集的樣本數設為 1，然后把 K 設為 1，并且設置只走一個梯度步，就變成了**在線 Q 迭代算法** (Online Q-iteration)，循環以下三步。 1. 執行某個行動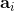，收集觀察數據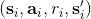。 2. 。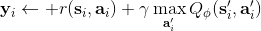 3. 。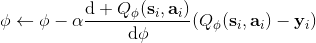 該算法每輪執行一個行動，得到一個轉移觀察，算出目標值，做一步的隨機梯度下降。這是標準的 Q 學習算法，雖然是離線的，但還是和剛才所說的一樣，第一步的支撐集希望足夠大。那么如何選擇行動呢？我們最終的行動服從一個單點分布，選擇一個使得 Q 最大的行動。但是如果我們把這個東西直接搬過來在學習過程中使用的話，是不好的。事實上，這是在線學習中的一個很糾結的問題：探索 (exploration) 和開發 (exploitation)。學習就是一個探索的過程，如果我們還沒進行足夠的探索，在 Q 函數還不夠準確的時候，我們根本無法分別出到底哪個是真正好的，會忽略掉真正優秀的方案。在在線學習中，有多種啟發式方法來脫離這一局面。一種策略稱為-貪心，也就是分給最大的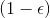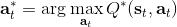的大概率的同時，也保留概率平均分給其他所有的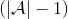種行動。另一種常用的設定是 Boltzmann 探索，概率分布為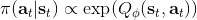。它假定 Q 函數多多少少知道一些哪個行動好，但是有噪音。這樣 Q 比較大的行動有顯著較高的概率被選到，同時保持了其他選項的可能性。 ## 算法的理論 讓我們回到非神經網絡近似的值函數迭代算法，它本質上在做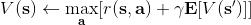。那么第一個問題就是，這個算法收斂么？如果是的話，收斂到什么？首先，我們定義一個備份算子 (backup operator) 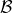 ，形式上寫作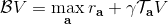，其中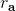是所有狀態下選擇行動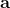的一步收益的向量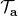，指的是選擇行動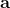的轉移矩陣，諸如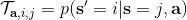，max 是按分量取最大。實際上，我們可以發現最優下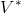，是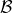算子的一個不動點，因為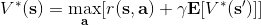，所以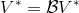。與之前 Q 函數的討論相似，這一個不動點總是存在，總是唯一，且總是對應著最優策略。現在我們的關鍵問題是如何去找到這樣一個不動點，因為不動點意味著最優值函數和最優策略。 我們可以通過證明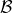是一個收縮映射 (contraction mapping) 的方式來證明值函數迭代法收斂到一個不動點。事實上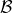，是一個無窮模下的收縮映射，因為對任何的兩個值函數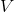和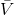，我們可以證明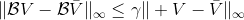，兩者的間隙每次都減小到原來的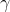倍。如果我們選擇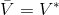的話，那么因為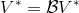，有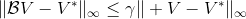。因此每做一次迭代，我們都能把兩者之差的無窮模稍微減小一些。 使用算子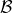，我們可以把每一步的值函數迭代算法寫成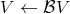。為了把 Q 函數用神經網絡表示，現在我們來看擬合值函數迭代算法。擬合值函數迭代需要做一個回歸，它的本質是從神經網絡能表示的所有函數的簇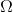里面，找到一個函數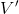，使得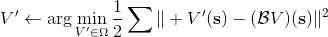。雖然在理論上，一個無限大的深度神經網絡可以擬合任意函數，但是在實際使用中，我們一般只能使用一個有限大小的神經網絡，因此它能表示的只是所有函數的一個子集。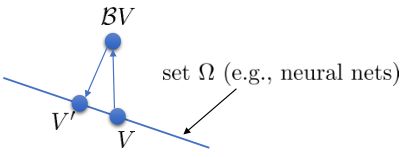  如上圖，藍色的線代表該神經網絡能代表的函數的全集，我們從一個函數出發，進行一次備份操作，然后使用最小二乘回歸來投影到這個函數集合。我們定義投影算子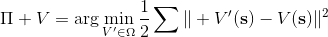，那么我們的擬合值函數迭代算法可以寫成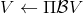這樣的復合映射。注意到投影算子最小化的是歐幾里得距離，是 2 模下的收縮映射。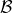是一個無窮模下的收縮映射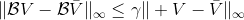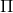，；是一個 2 模下的收縮映射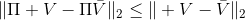，，但問題在于如果我們將這兩個映射進行復合，那么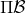并不是一個收縮映射，因為它們不是在同一個模下收縮的。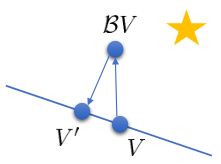  上圖是一個該算法發散的例子。假設最優解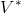在那個五角星處，然后我們從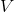開始一腳走到了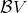，然后被投影回歸扯回了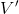。從圖上看，我們的解到最優解的距離越來越遠了。注意到，不用無窮模的原因是當狀態空間很大或者無限的情況下，無窮模下的投影問題極其難解。我們只能尋求找到最優解的一個投影（同樣對于策略梯度法我們也只能期望找到最優策略的一個投影），但是事與愿違的是，反復進行擬合值函數迭代算法，可能使你從較好的解開始越來越差。因此我們的結論是，值函數迭代法在表格中是收斂的，但是擬合值函數迭代法在一般意義下是不收斂的，在實踐中也通常不收斂，但是有一些方法來緩解這些問題。 擬合 Q 函數迭代法也差不多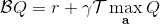，，只是把 max 放到里面去了；同樣投影算子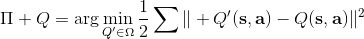，因此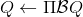。它的收斂結果與之前也別無二致，同樣一般意義下不收斂。對于在線 Q 迭代算法來說，它的第三步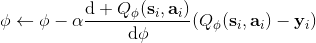看起來在走一個梯度步，我們看似抓住了一個救命稻草：梯度下降法應該是可以收斂的？但是，Q 函數方法的梯度并不是目標函數的梯度，因此與策略梯度法并不同，它并不是梯度下降法。 這個不收斂結論同樣也適用于演員-評論家算法。如一步自助法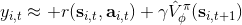關于無窮模收縮，而擬合函數 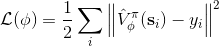關于 2 模收縮，因此擬合下的自助法做的策略評估同樣不具有收斂性。順便說一下，在演員-評論家算法中用的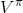，指的是關于策略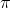的值函數，是評論家用的函數；而在值函數迭代中用的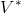，則是最優策略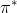所代表的值函數，也是最優的值函數。 在這一篇中，我們暴露了很多問題，而在接下來的內容中，我們將嘗試如何緩解這些問題，從而讓算法能正常運轉起來。