# (7) 深度增強學習中的 Q 學習方法 > 作者：[謝天](https://www.zhihu.com/people/xie-tian-55-77) > > 來源：[POST 館](https://zhuanlan.zhihu.com/c_150977189) ## 回放緩沖池與目標網絡 在上一篇中，我們介紹了一些純粹使用值函數的方法（這個是在動態規劃中最最經典的要素），最重要的是 Q 學習方法，這類方法拋開了一個顯式的策略，直接去學習 Q 函數，使我們知道在某個特定的狀態下執行某一操作效果有多好；也指出了如果我們使用神經網絡來進行擬合所可能出現的不收斂現象：這些問題將在所有的使用某些結構（如神經網絡）擬合值函數，然后使用擬合的值函數作為“評論家”來做自助的方法中都存在。在這一篇中，我們將介紹一些方法，使得在實踐中這些問題能被有效克服。 在 Q 學習中，我們已經介紹過，可以使用擬合 Q 迭代的方法：在每一輪迭代中，使用某些策略收集很多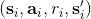的樣本，然后執行若干步構造目標值和回歸的過程。當然我們希望收集到的樣本的支撐集越大越好，以避免盲區。它的一個特例是在線 Q 迭代，也就是每次只收集一個樣本，構造目標值，然后回歸只走一個簡單的梯度步。我們僅以在線 Q 迭代算法為例，它循環執行以下步驟（此處目標值已經填入）。 1. 執行某個行動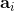，收集觀察數據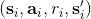。 2. 。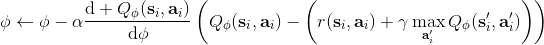 我們之前已經說明過，它**不是一個梯度下降算法**，因此，梯度法的收斂性在這里不適用。第二點很關鍵的問題是，在普通的 SGD 中，我們常常認為每一次拿到的數據之間都有一定的不相關性；而在第一步收集的數據中，**數據通常都是非常相關的**：下一步的觀察數據可能和這一步非常相關。因此，梯度也會非常相關。因此，我們會嘗試去使用一些手段來緩解這些問題。我們考慮解決的問題主要有兩個：序貫狀態的強相關性，以及目標值總是在變動。  序貫樣本為什么會成為痛點？讓我們先考慮一個簡單的回歸問題，這個回歸問題嘗試去擬合一堆數據，而這堆數據是一個正弦波。一般我們希望數據是獨立同分布的，而我們在序貫問題中先得到了開始的幾個樣本，然后逐漸得到后面幾組，每得到一組我們就走一個梯度步。這樣我們就很難去學習整個正弦波，而更容易在局部形成過擬合的同時，忘掉了其他樣本的信息。在演員-評論家算法中，可以采用一些并行學習的方法，這里 Q 學習也可以：使用多個獨立的智能體進行獨立的數據收集，然后使用同步或者異步的方法進行梯度更新，這樣可以使得樣本的相關度減輕，但是這樣的做法可能是相當“繁重”的。 另一種更常見的做法，**回放緩沖池** (Replay Buffer)，利用到了 Q 學習算法本質上是離線 (off-policy) 的這樣一個性質：也就是說，Q 學習算法使用到的數據不需要根據當前的策略收集得到。相對的，演員-評論家算法是一個在線 (on-policy) 算法，因此對于演員-評論家算法來說并行學習是首選之一，然而在 Q 學習中并非如此。在擬合 Q 迭代算法中，我們每一步收集一些樣本，然后進行若干步目標值構造和回歸。在收集樣本的步驟中，我們可以使用任意策略（當然我們希望樣本的支撐集足夠大），因此我們不妨假設一個極端情形：收集樣本的步驟被完全省略了，我們在很早的時候就收集了非常非常多的樣本，然后全部丟在了一個數據庫之中，我們在每次訓練更新的時候隨便從里面拉出一些來。這樣做完全是可以的，因為我們事實上不根據策略和模擬器進行任何交互。 這給了我們一個啟示，我們可以構造一個樣本池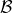，然后每次從里面抽出一批樣本，進行梯度更新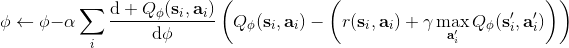：  。這樣做的好處不僅在于這樣抽出的樣本不再具有很強的相關性了，同時我們每次可以用的樣本量也從 1 個變成了很多個，可以使用多樣本來降低梯度的方差（有點類似于 mini-batch SGD 的做法）。現在我們想要知道的是，高覆蓋面的數據到底從哪里來。在實踐中，對于很大的狀態空間，我們通常很難去很好地覆蓋；我們能做到的最好情況的可能也只是覆蓋我們所可能到的滄海之一粟。因此，我們在 Q 學習的過程中，還是需要同時去為樣本池補充新鮮血液。這也要求我們使用一些探索策略向外界環境輸出一些不同的策略，然后得到樣本進入樣本池。訓練過程有點像某些抽獎箱子里每次抽一張卡，抽完丟回去再抽。因為我們投入的數據會被反復使用到，有點類似于回放，因此被稱為**回放緩沖池** (Replay Buffer)。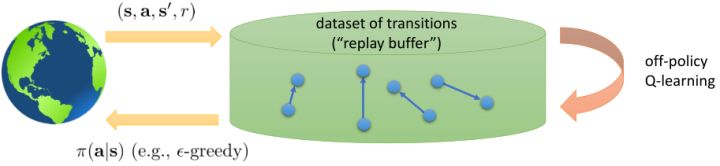  從而，一個（同步的）使用回放緩沖池的 Q 學習算法是這樣的： 1. 使用某些策略（如-貪心）跟環境打交道收集一批數據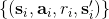，并加入到回放緩沖池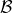中。 2. 從回放緩沖池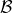中抽一批樣本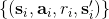。 3. 更新一個梯度步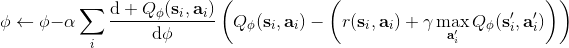：，反復執行 2-3 步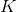次之后返回第一步繼續收集樣本。 注意到，如果緩沖區足夠大的話，那么新進入數據占權重其實是很小的，很可能不會被抽到。當然這不是個問題，新進數據只是為了讓樣本池的支撐集更廣（更新 Q 函數使得更新策略，新策略會訪問到之前沒去過的地方）而已。在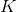的選擇上，通常選擇 1 就不錯，然而如果數據獲取代價比較高的話（如需要與真實物理系統打交道），更大的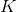有時候會產生更高的數據使用效率。由此，回放緩沖池成功解決了數據的強相關性問題，但是目標值的變動問題還是沒有解決。 之前聽過一個童話，說小豬問媽媽幸福在哪里，媽媽表示在尾巴上，然后小豬嘗試咬自己尾巴但是抓不到，但是媽媽表示只要你一直走幸福就會一直跟著你。暖心的小童話在這邊就變成了一個討厭的事實：我們想要使得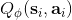盡量靠近目標值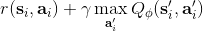，但只要我們不停迭代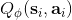，我們的目標值就跟尾巴一樣一直會動來動去的！這就跟射擊中的移動靶一樣，總比固定靶要難打很多。但是如果我們能夠像之前一樣，先把目標值算出來，然后再去做最小化最小二乘的回歸，那么這樣的回歸就會穩定很多。 在這里，我們把之前的思想改造成一個**目標網絡** (Target Network)，以提高實踐中的穩定性（雖然還是沒有什么理論保證）。整體想法與之前使用回放緩沖池的 Q 學習算法沒有什么太大區別，只不過是我們再執行若干步（如 10000 步）整個算法迭代后，就把整個網絡的參數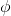存下來稱為目標網絡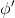（就像很多軟件的自動存檔功能一樣），然后我們每次做的梯度步變成了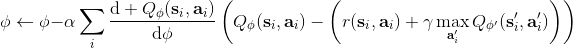，也就是說我們的目標不再是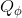而是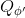了。這樣就能使得我們的“靶子”在一段時間內保持確定，不再是每走一個梯度步目標就動一下，就像“秦王繞柱走”一樣的“放風箏”策略一樣避敵。等我們已經足夠接近靶子了，然后再允許靶子動到一個更好的地方去。我們可以發現，如果我們把靶子固定，那么這個算法非常接近一個監督學習算法。這跟人一樣，一開始學走路就把步伐放得太大容易摔跤，我們這樣做可以把訓練速度放下來，同時提高訓練的穩定性，從而這個目標網絡更新步數需要權衡以提高收斂概率：太大訓練太慢，太小則容易不穩定。理論上，這樣做不改變任何事情，但是實踐中，這樣降低靶子移動的頻率，非常有助于訓練的穩定性，減少訓練所需要的時間。綜合這兩種技巧，Mnih et al. (2013) 在 NIPS 提出了舉世聞名的深度 Q 網絡 (Deep Q Network, DQN) 算法，也是深度 Q 學習中最經典的算法。 1. 在環境中執行某個操作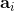，觀察到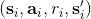，并加入到回放緩沖池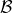中。 2. 均勻地從回放緩沖池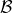中抽取一個小批量樣本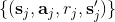。 3. 使用目標網絡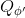，計算出目標值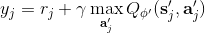。 4. 走一個梯度步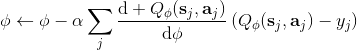，。 5. 每隔步，把整個神經網絡的參數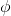復制到目標網絡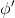中去。返回第一步。 小批量樣本的特性是，其中第三第四步是可以并行的。  關于目標網絡，也有另一種實現策略。看上圖，我們在第一個綠色方塊更新了目標網絡，此后若干個步驟，我們都將以這個目標網絡為基礎進行迭代，然后逐漸誤差越來越大，直到下一個目標網絡更新點，就形成了一個斷點。這樣其實對于步驟和步驟之間并不公平，有些步驟訪問的延遲很高，有的步驟則很低。為了使得延遲公平化，可以使用一個類似于指數平滑的方法（隨機優化中的 Polyak Averaging），不再是若干步執行更新而是每一步都做一個小變動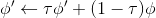：。實踐中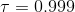效果不錯。從優化的角度，可以對這樣的做法有一些理論解釋。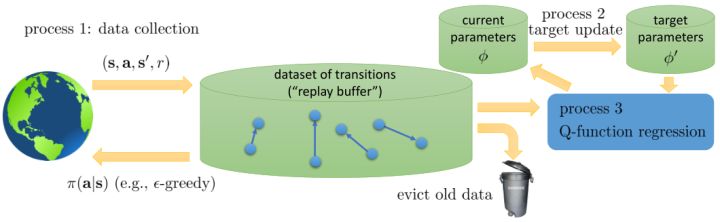  現在，讓我們對在線 Q 學習、擬合 Q 迭代、DQN 算法進行一個比較。我們可以發現，對于有回放緩沖池和目標網絡的 Q 學習算法來說，最外層循環是更新目標網絡的參數，內層循環是使用同一個策略收集若干數據集丟進緩沖池后，迭代若干次從池中抽樣然后做小批量樣本的梯度步；而對于擬合 Q 迭代算法，最外層循環是使用同一個策略收集若干數據集丟進緩沖池，而內層循環則是更新目標網絡的參數，然后迭代抽樣做梯度步。外面兩層操作順序是相反的。DQN 是其中的一個特例。 從而，我們可以把過程的主要步驟分為三部分：第一步是數據收集 (data collection)，第二步是目標更新 (target update)，第三步是 Q 函數回歸 (Q-function regression)。此外，還有一個從緩沖池里丟棄舊數據的操作。第一步的數據收集是用于充實我們的緩沖池的。我們拿我們有一定探索性質的策略與外界打交道，從而獲得一些轉移數據；如果緩沖區太大了，我們也需要把一些舊數據丟進垃圾桶（如把緩沖區弄成一個固定大小的循環型，老的數據自然被丟棄），這是因為舊數據可能是在很垃圾的策略下得到的，已經沒什么實際價值。第二步以一定的頻率（或者 Polyak Averaging）用當前的參數去更新目標網絡參數，如果我們想穩定一點的話，這一步通常頻率很低。第三步是一個學習過程，它從目標網絡中取得參數，從緩沖池中取得數據，然后進行回歸以后更新當前的參數。廣義看，不同的算法之間，只在于這幾個操作的頻率有所區別，取決于樣本取得代價，網絡更新代價和對穩定性的需求。對于在線 Q 學習，我們取得數據后只使用一次就丟棄了（也就是樣本池里只有一個樣本），三個步驟的頻率是一樣的。對于 DQN，緩沖池比較大，第一步和第三步運行頻率一致，而第二步頻率很低。對于擬合 Q 迭代，就形成了一個嵌套結構，第三步是第二步的內循環，而第二步是第一步的內循環，頻率指數降低。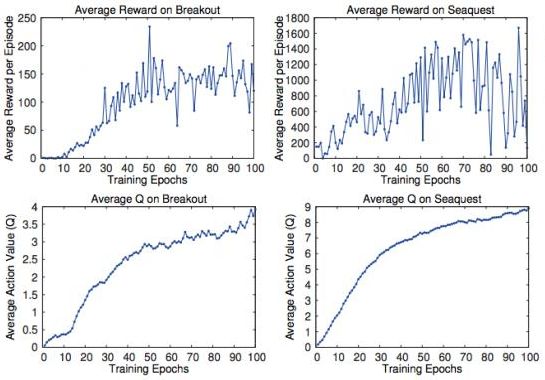 ## 讓 Q 學習更好的技巧  我們在前面已經知道，Q 函數本身是有意義的：在某個狀態下，我們進行了某種操作，今后會帶來的期望收益。那么我們使用之前估計得到的 Q 函數值是否能準確反映呢？Mnih et al. (2015) 在 Nature 上的論文做了一系列正面實驗。上面四個圖中，上面兩個是平均收益，下面兩個是平均 Q 值，我們發現當估計的 Q 值上升的時候，總體來說收益也呈一個上升的趨勢；但是在訓練片段中收益波動相當大，Q 值雖然不能很好去擬合收益，但是波動相對小，相對光滑。下面舉兩個 Atari 游戲的例子來說明這些值函數的意義。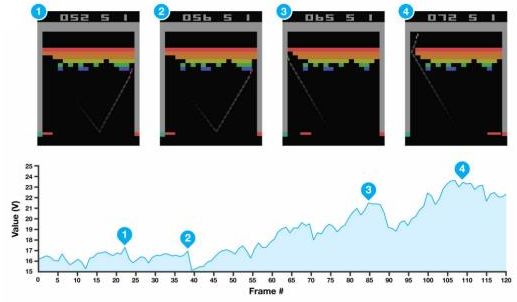  在打磚塊 (breakout) 游戲中，我們知道每當球撞到一個磚塊，就會產生一個小小的收益，因此，值函數就會有一個小型的峰出現。上面四個圖每次都是要打掉一個磚塊時的畫面，正好對應了下面的四個峰。更進一步地，我們一個很好的策略是讓這個磚塊里面產生一個小孔，然后讓球進去那個基本封閉的區域里面跳來跳去，打掉很多磚塊產生大量得分：這個判斷正好和圖 3（成孔前夕）-圖 4（成孔后進入）一致，從而值函數給予了很高的評分：圖 3 是一個希望，而圖 4 美夢成真。這說明我們的值函數的局面評估定性上是合理的。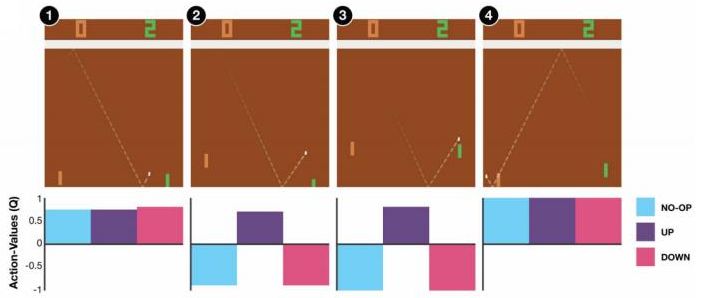  在彈球游戲 (pong) 中，我們控制右邊的板子上下移動來接球。操作有三種：無操作、向上、向下。在圖 1 和圖 4 中，三種操作都可以接受，尤其是在圖 4 中我們不管做什么樣的操作都已經獲勝了；而圖 1 中接小球還有足夠的容錯可能。而在圖 2 則接小球有了很強的緊迫性，而圖 3 緊迫性更強幾乎沒有容錯機會了，所以向上的 Q 值很高，向下和不動的 Q 值很低。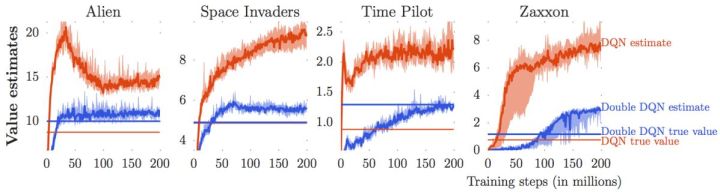  我們說了很多使用值函數評估局面、Q 函數來做決策的合理性。因為我們只需要按照 Q 函數最大的準則來進行行動，似乎只有 Q 的相對數值大小才有決定性作用。那么這些絕對數值是否準確？很遺憾，van Hasselt et al. (2015) 這些數值是被高估的。我們只看上圖的紅色部分（DQN estimate 和 DQN true value）。紅色的波動很厲害的那條折線代表了神經網絡所估計出來的 Q 值，而下面那條紅色直線是根據 DQN 的策略行動實際所能得到的期望收益：所以理想情況下，在很多步估計之后，紅色折線應該和紅色直線有一個相切關系。但是事實上，我們在不同的游戲中都發現估計出來的紅色曲線明顯比真實值紅色直線要高，呈現一個系統性趨勢。這說明了 DQN 實際上嚴重高估了 Q 值。事實上 DQN 的表現還是不錯的，盡管這個 Q 值可能估計得很離譜：實際上對于兩個不同的操作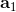和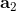，只要讓估計的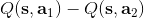差和真實值差不多或者長得像就能讓 DQN 工作起來。 這樣的**高估** (overestimate) 現象在 DQN 中是系統性問題，原因出在目標值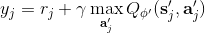的后面那個 max。我們選擇最大的那個數會產生怎樣的結果呢？考慮兩個隨機變量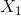和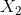，我們有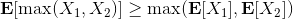。這個結論在多個隨機變量中也是適用的。想象一下，這些變量都有一些噪音，而取 max 操作則擴大化了這些噪音，在這種情況下我們是關于噪音取 max，可能我們找到的是若干個數中噪音最大的那個。我們的 Q 都是從樣本軌跡里學出來的，所以都含噪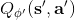，即便接近真實的 Q 值但也都是不完美的，因此我們可能得到的只是噪音最高的選項而不是真正 Q 最大的選項。注意到一個簡單的事實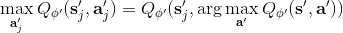，，它點明了這一問題的來源。如果對于某一行動 Q 值過大了，我們做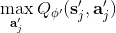過高估計了接下來行動的值，然后繼續傳導到后續的迭代中去。我們的決策選擇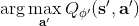本身就是來自于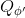，而我們所選用的 Q 函數值也同樣來自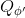。 van Hasselt et al. (2010, 2015) 的**雙重 Q 學習** (Double Q-learning) 技術用于緩解這一問題：它本身希望切斷**過高估計的行動 - 過高估計的值的傳導**這樣的一個鏈條。如果最大 Q 決策選擇和它對應的 Q 函數的相關性被斬除，那么這就不再是一個問題了。雙重 Q 學習的想法就是，不要使用同一個網絡來確定行動和估計 Q 函數值。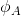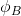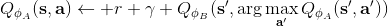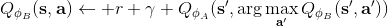它使用兩個網絡和，更新時候采用以下交錯手段： *  *  也就是說，更新一個網絡的時候，使用另一個網絡的值。如果兩個 Q 網絡的噪音的來源不同，那么它的噪音就不再如此容易擴大了。在實際中，我們在前面已經介紹了目標網絡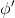了，因此事實上我們已經有兩個不同的網絡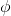和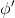了，可以把它利用起來！在標準的 Q 學習中，我們使用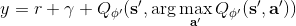，而在這里我們只需要稍作修改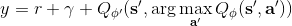，，用當前網絡來確定我們選擇哪個行動，而用目標網絡來評估 Q 值。在實踐中，我們遇到的問題就會被很大程度上緩解。 我們使用 Q 學習，在回歸中會設置一個目標值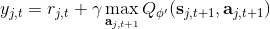。這個目標值信號來自于兩塊，一塊是當前的收益，一塊是 Q 值代表的未來期望收益。如果訓練還是在早期，通常 Q 就比較小（初始化為小的隨機數），那么當前收益就會成為主要成分，Q 值只是噪音。對于時間較長的問題，如果 Q 已經訓練到比較后期了，從數值的量級上考慮，可能當前收益所占比就很小，Q 值所占比較大。如果 Q 占比比較大，那么這個目標值可能不太好，只有一期的收益，剩下都由 Q 來決定。在[演員-評論家算法](https://zhuanlan.zhihu.com/p/32727209)中，我們已經提到了這樣的自助法存在最低方差的好處，但是如果 Q 值不準確就會帶來最大的偏差；而如果我們不使用自助法而直接看一條軌跡，那么將是無偏的，但是方差巨大。從而，我們介紹了一個折中的方法，就是使用步收益后再把未來的自助項加進去。轉化到我們當前的問題中就是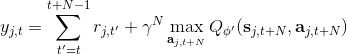。 使用步收益的主要好處是，可以降低 Q 函數估計不準確所導致的目標值的偏倚（但同時增加了方差），同時尤其是在早期訓練中有效提升速度；但是它也帶來嚴重的根本性問題，這樣的訓練只有在在線訓練的時候才是正確的！為了解釋這一問題，我們回憶我們的策略是由 Q 函數決定的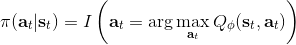：；而我們在上面使用步收益，估計的其實是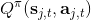，而我們所有的轉移，對于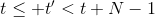的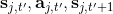，都是要從當前的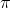里面來的。我們之前沒有這樣的問題是因為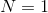，不涉及到在線的轉移問題。那么怎么處理這一問題呢？第一種做法是，**直接忽略掉這個問題**。在理論上這是不能接受的，但是實際中通常效果還不錯。忽略能否可行，跟待解決問題本身是緊密相關的。第二種做法是**切割軌跡**以得到在線數據。也就是說，我們可以把之前的片段拿過來，然后一步步看我們的策略是否支持這樣的行動，如果出現了分歧那么就直接切斷：從而這個片段的前面部分是符合我們當前策略的，可以作為一個在線數據使用。這樣的做法當數據主要是在線數據（我們需要及時淘汰舊數據）且行動空間很小（如 pong 彈球游戲只有上下和不動三種操作）時效果不錯，而如果行動空間很大時則幾乎不可能起到什么作用。此外，也可以考慮跟策略梯度法一樣做**重要性抽樣**重新加權，這樣得到的估計總是無偏的，具體可以參考 Munos et al. (2016)在 NIPS 上的文章：Safe and efficient off-policy reinforcement learning。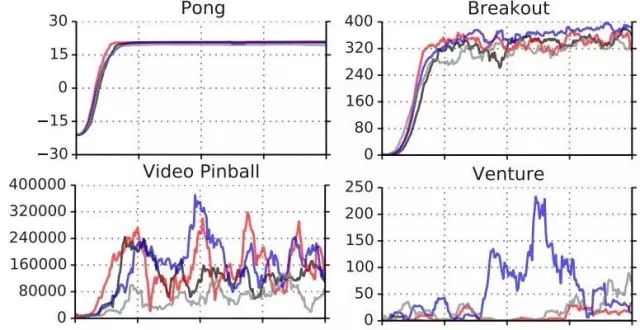 春季課程中，Schulman 還請他的同事 Szymon Sidor 總結了一些經驗，和 Levine 教授這邊混在了一起：  1. 上圖顯示了幾個問題的幾種不同 Q 學習的效果 (Schaul et al., 2015)。發現對于不同的問題，Q 學習在有些問題上很可靠，在有些問題上波動很大，需要花很多力氣來讓 Q 學習穩定下來。因此發現幾個能讓 Q 學習比較可靠的問題來試驗程序，譬如 Pong 和 Breakout。如果這些例子上表現不好，那就說明程序有問題。 2. 回放緩沖池的大小越大，Q 學習的穩定性越好。我們往往會用到上百萬個回放樣本，那么內存上怎么處理是決定性的。建議圖像使用 uint8 (1 字節無符號整型) 存儲，然后在存儲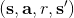的時候不要重復存儲同樣的數據。 3. 訓練的時候要耐心。DQN 的收斂速度很慢，對于 Atari 游戲經常需要 1000-4000 萬幀，訓練 GPU 也得幾個小時到一天的時間，這樣才能看出能顯著地比隨機策略要來的好。 4. 在使用貪心等策略的時候，一開始把探索率調高一些，然后逐漸下降。 5. Bellman 誤差可能會非常大，因此可以對梯度進行裁剪（clipping，也就是設一個上下限），或者使用 Huber 損失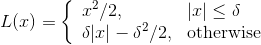進行光滑。 6. 在實踐中，使用雙重 Q 學習很有幫助，改程序也很簡單，而且幾乎沒有任何壞處。 7. 使用步收益也很有幫助，但是可能會帶來一些問題。 8. 除了探索率外，學習率 (Learning Rate, 也就是步長) 也很重要，可以在一開始的時候把步長調大一點，然后逐漸降低，也可以使用諸如 ADAM 的自適應步長方案。 9. 多用幾個隨機種子試一試，有時候表現差異會很大。 ## 行動空間連續時的 Q 學習 在我們之前的問題中，通常假設策略很容易得到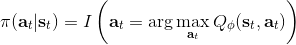：，求 max 只需要遍歷行動空間就行了；目標值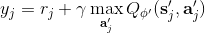的 max 也是這樣。但是如行動空間是連續的時候，這個 max 就不容易做了。這個問題在后者中尤其嚴重，因為它是訓練過程中最內層循環要做的事情，頻率比前者要高多了。那么如何做 max 呢？ 第一種想法是直接做優化。在最內層循環做基于梯度的優化算法（如 SGD）相對來說是比較慢的。注意到我們的行動空間通常都是比較低維的（相對整個系統而言），不使用梯度信息的隨機優化也許能有用武之地。最簡單的方法是使用離散隨機踩點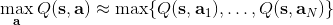：，其中行動是從某些分布（如均勻分布）中得到的。這個方法是最簡單的，而且還比較容易并行，但是這樣得到的結果是不準確的，尤其是在維度增加的情況下看起來就不像是能找到一個效果很好的解；不過有些時候，我們也不真正在乎優化求解的精度。此外，還有一些更好的方法，譬如交叉熵方法 (Cross-entropy Methods) 這樣的迭代隨機優化算法，或者如 CMA-ES (Covariance Matrix Adaptation Evolutionary Strategies) 這樣的進化算法。這些通常在不超過 40 維的決策問題中有效。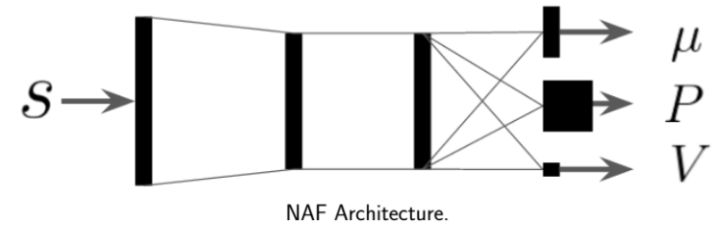  第二種方法是，我們選取一個比較容易優化的函數簇來擬合我們的 Q 函數。在此之前，我們適用的都是通用的神經網絡來擬合 Q，有些情況下我們不必要這么做。譬如在 Q 函數是二次函數的時候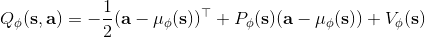，，我們就訓練一個神經網絡或者其他結構，輸入狀態，輸出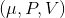，其中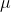和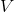都是向量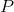，是矩陣（可以用如低秩形式表示）。這樣的方法稱為 NAF (Normalized Advantage Functions)，它的天然特性就是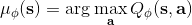和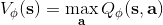。這個很容易和高斯分布建立起聯系；當然，這樣的 Q 函數中行動是沒有界限的。我們這么做的話，算法上不需要做任何改變，非常容易，而且和原來的 Q 學習一樣高效。但是缺點就在于 Q 函數只能是固定的形式（如這里的二次函數），非常受限，Q 函數的建模泛化能力將大大降低。 第三種方法比第二種方法更為廣泛，是去新學習一個最大化器，在 Lillicrap et al. (2016) 在 ICLR 上的一篇文章中被作為 DDPG (Deep Deterministic Policy Gradient) 算法介紹。考慮到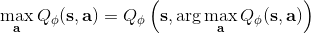，可以想的是另外訓練一個最大化器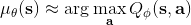，作為最大化的算子。訓練的方法是，讓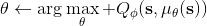，這個可以用梯度上升法，梯度可以遵循鏈式法則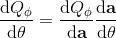：。從而，我們的目標值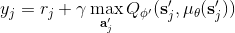。整個 DDPG 算法迭代執行以下步驟： 1. 在環境中執行某個操作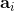，觀察到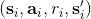，并加入到回放緩沖池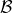中。 2. 均勻地從回放緩沖池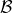中抽取一個小批量樣本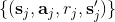。 3. 使用目標網絡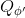和最大化器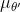，計算出目標值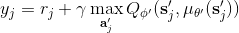。 4. 當前網絡走一個梯度步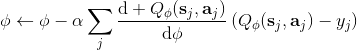，。 5. 最大化器走一個梯度步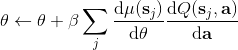，。 6. 使用 Polyak Averaging 更新和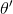。 相當于相對 DQN，只是增加了一個最大化器，第三步使用最大化器，第五步更新最大化器，同時最大化器的更新也是用 Polyak Averaging。 Q 學習有很多應用。Lange and Riedmiller (2012) 使用擬合 Q 迭代的方法控制小賽車（和其他低維度系統），因為較早期，所以擬合的函數簇包含了隨機森林和神經網絡。它們是訓練了一個自編碼器 (autoencoder) 來降維，在隱層上面做 Q 學習。這是同時出現 Q 學習和神經網絡比較早的論文，但是 Q 學習沒有和神經網絡直接結合起來。兩者直接結合起來，產生的最經典的 DQN 出自于 Mnih et al. (2013) 在 NIPS 上的文章，用同一種方法成功攻克了多種 Atari 游戲。它們的訓練直接使用圖像，而不是在一個隱空間中訓練。這個工作使用了回放緩沖池和目標網絡的技術，使用了一步的備份和一步的梯度步。這個結果在后來也有很多技巧可以改進，如雙重 Q 學習。Lillicrap et al. (2015) 最早提出了 Q 學習在連續控制（簡單機器人模擬器）上的應用，即 DDPG。這項工作考慮連續的空間，并使用了一個最大化器網絡；采用了回放緩沖池、目標網絡、Polyak Averaging 更新等技術，使用了一步的備份和一步的梯度步（與 DQN 一致）。Gu et al. (2017) 使用 Q 學習法控制真實的機器人。這項工作同樣考慮連續控制，對 Q 函數采用了二次函數的 NAF 近似，也同樣采用了回放緩沖池和目標網絡技術。在收集數據上，使用了多個不同的機器人來并行處理。因為是真實物理場景，數據比較難采集，所以每個模擬步走了 4 個梯度步（一步備份）。