# (9) 用數據擬合模型 > 作者：[謝天](https://www.zhihu.com/people/xie-tian-55-77) > > 來源：[POST 館](https://zhuanlan.zhihu.com/c_150977189) ## 基于模型的增強學習：框架 在上一篇中，我們在假設模型動態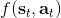已知的情況下，發現可以利用模型動態做很多事情。在連續控制中，我們提到了使用 iLQR/DDP 的軌跡優化方法，這些方法主要要用到模型動態的一階微分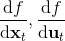；我們甚至了解到，Tassa et al. (2012) 使用 iLQR 做模型預測控制，在我們知道模型是什么的情況下可以不通過學習步驟制定出非常魯棒的控制（使用 MPC，哪怕模型是錯的，也有很強的魯棒性）。如果我們不知道模型的話，要利用這個方法，就得去學習這個模型，然后對其進行微分。在離散問題中，我們也提到了蒙特卡洛樹搜索 (MCTS) 方法。在 MCTS 方法中，我們要去模擬狀態的轉移，就要知道模型系統的動態，這樣我們才能返回到祖先節點進行其他行動的搜索。因此，如果我們知道模型動態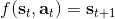，或者隨機的分布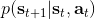，那么我們就可以使用上一篇的方法。因此我們考慮去從數據中學習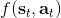，然后根據它來進行之后的計劃。這樣的方法被統稱為**基于模型的增強學習** (model-based reinforcement learning)。 一個最簡單版本的基于模型的增強學習算法（v0.5 版），執行以下三步： 1. 運行某種基本策略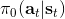（如隨機策略）來收集樣本數據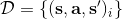。 2. 通過最小化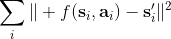的方法來學習模型動態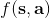。 3. 根據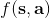來計劃未來行動。 第一步的策略對于駕駛汽車來說可能是隨便轉方向盤，顯然不是什么好策略，但是也可以用這個來得到一些數據。第二步是去構建一個損失函數并最小化用模型預測出來的狀態和真實發生的狀態來擬合。第三步則是使用上一篇中的方法來進行計劃。這樣簡單的方法在有些時候也可以起作用。本質上，這正是經典機器人學中系統識別 (system identification) 問題中在使用的方法：現在已經有一個參數形式的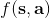了，如已經有了機器人的運動方程，但是很多參數譬如質量和長度什么的不知道，而需要通過回歸等方法去估計（有點像待定系數法）。此外，這樣的方法中，這個“基本策略”還是要有所講究的：譬如說不能總是執行一個行動，因為這樣我們學習到的模型可能無法適應很多從來沒見過的行動；即便基本策略執行各種情況，但是執行它可能錯過重要的狀態空間部分，這樣也是不行的（當然這個說法本身就很玄學了）。總體來說，這個 v0.5 版本對于我們有一個利用物理知識手工推導的模型系統動態方程（我們有豐富的先驗知識），只有個別（如 10-30 個）參數不知道的情況下還是很好用的：這時候隨機策略可能足夠好。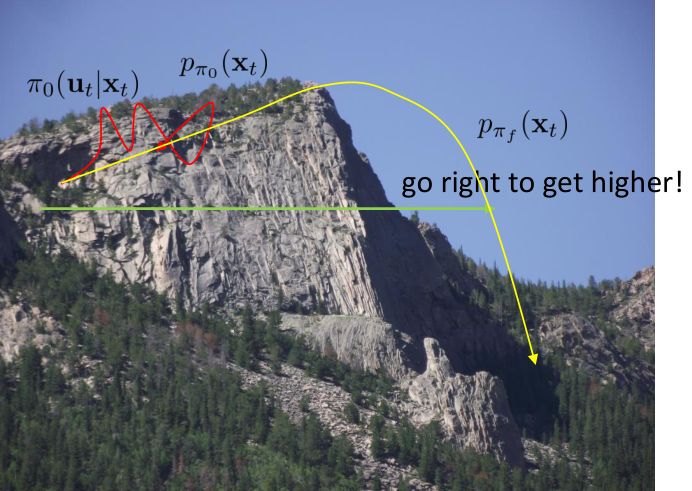  但在一般情況下，v0.5 版本明顯是有缺陷的。如現在智能體在這樣一個斜坡坡面上訓練，我們的目標是到達山頂。我們第一步進行一些隨機走動，訓練數據如紅色曲線；然后我們需要擬合一個模型，來預測行動如何影響智能體的高度（因為我們的目標是盡可能往高處爬）：我們通過紅色部分的數據，得到的結論可能是越往右走，高度越大；最后一步，我們使用這個模型去進行規劃，得到的結果就是如黃色軌跡一般墜落山崖。這里出現的問題主要就是如我們之前在[模仿學習](https://zhuanlan.zhihu.com/p/32575824)一篇中講到的**分布不匹配** (distribution mismatch) 問題：我們的訓練數據分布和實際遇到的情況不匹配。在這里，我們通過分布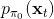來收集數據，但是實際用于規劃行動時，我們不再執行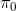下的分布，遇到的是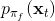，與之前遇到的分布是不同的。即便我們訓練了一個在分布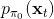下很好的模型，但這個模型在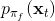所遇到的狀態下可以任意差。值得一提的是，這樣的分布不匹配問題在使用越具表達力的模型簇時越嚴重。因為如果像我們跟前面所說的一樣只缺少幾個待定參數，而模型具體形式已經知道了，那么其實對數據要求還是不高的；而使用如深度神經網絡這樣具有高表達力的模型，則會把紅色部分的數據擬合得相當好（_ 我覺得是一種過擬合 _），然后嘗試去遵循這個模型，就掉下去了。因此，越具有表達能力的模型事實上能越好地擬合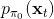分布下的數據，而這并不代表我們更加了解實際面對的分布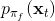。 為了解決這個問題，我們跟之前模仿學習相似，收集更多我們更關心的“實際分布”下的數據，以使得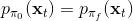。因此我們的 v1.0 版基于模型的增強學習算法如下： 一個最簡單版本的基于模型的增強學習算法（v0.5 版），執行以下三步： 1. 運行某種基本策略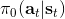（如隨機策略）來收集樣本數據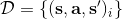。 2. 通過最小化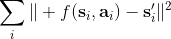的方法來學習模型動態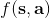。 3. 根據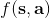來計劃未來行動。 4. **執行這些行動，并得到一系列結果數據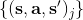加入到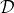中。反復執行 2-4 步。** 前三步與 v0.5 版無異，而 v1.0 版增加了第四步，收集新數據加入樣本中并重新學習模型動態，希望藉此消除分布不匹配的問題。這個算法和 DAgger 不同，因為 DAgger 是為了適應策略的改進，而這里只是一些獨立的強化學習步驟。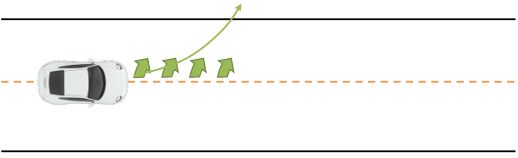  現在我們再對這個算法進行一些改進。考慮到如果我們犯了一個錯誤如何糾正：如果智能體失足墜落山崖，那么它就犧牲了，沒什么進一步好做的了，這個是致命錯誤；但并不是所有錯誤都是致命的。如我們駕駛一輛車，每次問我們的模型，如果我們方向盤朝正前方，那么汽車會往什么方向走？然后模型總是回答，會稍微往右一點點：實際答案是我們的車會往正前方開，但是稍微往右一點點這個答案也相當接近正確答案了。但是麻煩在于，如果我們按照這個模型去行動，每一個時刻開車我們都以為需要加一些向左方向進行補償，每一時刻方向盤都向左一點點的話，加起來很快這個車就會開出道路了。因此，即便我們的模型只有些許錯誤，我們在每個時刻嘗試進行一些補償，那么最后這些補償加起來會成為很嚴重的錯誤。  基于模型的增強學習 v1.5 版跟上一篇中的穩健算法類似，進行一些 MPC。如果我們發現根據我們的規劃走，這個車卻向左偏了，當誤差到一定程度時，我們就可以重新進行規劃，希望這個重新規劃的方法可以補償。框架如下： 1. 運行某種基本策略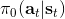（如隨機策略）來收集樣本數據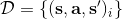。 2. 通過最小化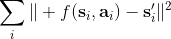的方法來學習模型動態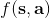。 3. 根據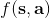來計劃未來行動。（如使用 iLQR） 4. **基于 MPC 的思想，僅執行計劃中的第一步行動，觀察到新的狀態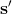。** 5. **將這一組新的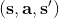加入到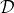中。反復執行若干次 3-5 步之后，回到第 2 步重新學習模型。** 也就是說，每次我們僅執行整個計劃序列中的第一步，然后走一步后對整個問題進行重新規劃。重新規劃路徑有助于解決模型誤差問題。第三步規劃做得越頻繁，每一次規劃需要達到的精度越低，可以容忍更差的模型和更糟糕的規劃方法。相對更簡單的規劃方法也可以起到作用，如可以接受更短的時長（也就是更加短視地規劃問題），甚至一些隨機采樣的方法經常也可以做得很好。Tassa et al. (2012) 的演示中就說明了即便模型很離譜，MPC 也在傾向于做一些正確的事情。 在這個 v1.5 版本中，最難的一點是做規劃。越精密的模型和方法，計劃未來行動的代價越大，使得在線進行越困難。如玩 Atari 游戲，然后使用 MCTS 的方法，那么計算代價就會相當高。而 Guo et al. (2014) 使用模仿學習訓練策略，則能更好地實現在線進行游戲。  MPC 方法可能很好，但是計算代價有可能會很大。我們之前的想法是構造一個策略函數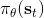來得到具體的行動。為了得到策略函數，我們可以寫出如上圖的計算圖來表明策略函數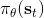如何影響收益，從而我們將梯度或者什么東西進行一系列反向傳播。這個做法對確定性策略非常容易，也能拓展到隨機策略。基于這種想法嗎，我們有了基于模型的增強學習算法 v2.0 版： 1. 運行某種基本策略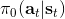（如隨機策略）來收集樣本數據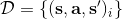。 2. 通過最小化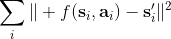的方法來學習模型動態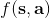。 3. **通過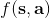，使用反向傳播的方法來優化策略函數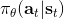。** 4. **執行**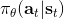**，將新的**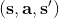**加入到**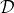**中。反復執行 2-4 步。** 在第三步，我們不再是去用某種方法來規劃未來路徑，而是使用收益的梯度通過反向傳播的方法來優化策略函數。第四步還是為了解決分布不匹配的問題，收集新數據用來重新訓練模型動態。需要明確的是， 只是去最小化損失函數，而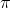 則是通過有點類似于 BPTT 訓練 RNN 的方法進行求解的。當然這個方法本身并不是很好的，主要原因和訓練 RNN 難度很大一致。我們的 可能是很復雜的函數，我們對其求導，然后反向傳播很多階以后梯度可能會消失或者爆炸，在數值上很病態。有一些技巧可以對這些問題進行改善。對以上四個版本的框架進行比較，得到以下小結： * v0.5 版：我們收集隨機樣本，訓練模型動態，并進行規劃。比較適合模型動態形式基本已知，只需要去求解少數參數的情形。優點在于方法簡單，沒有迭代過程；缺點主要在于分布不匹配問題。 * v1.0 版：針對分布不匹配問題，采用交替進行收集數據和重新訓練模型并規劃的方法。優點在于同樣簡單，而且解決了分布不匹配的問題；缺點在于它還是一個開環控制過程，在誤差下容易出現“小車跑出道路”的問題。 * v1.5 版：在 v1.0 版的基礎上加入了 MPC 進行閉環控制，在每一步運行后進行重新規劃。優點在于對小的模型誤差魯棒性較好，在模型不準確的時候也可以得到很好的控制；缺點在于它的計算代價比較大，需要一邊在線運行規劃算法，一邊收集數據。 * v2.0 版：不再使用 MPC 進行反復重新規劃，而考慮構建一個策略函數，通過反向傳播去更新策略函數。優點在于它在運行時計算代價較小，只需要根據策略函數執行行動，比規劃算法容易很多；缺點在于它可能在數值上非常不穩定，尤其是在一些隨機域之中。 這些算法很多都已經被用于實際問題中。如 Deisenroth et al. (2011) 在 RSS 的一文"[Learning to Control a Low-Cost Manipulator using Data-Efficient Reinforcement Learning](http://link.zhihu.com/?target=https%3A//rse-lab.cs.washington.edu/postscripts/robot-rl-rss-11.pdf)"中，使用 PLICO (Deisenroth and Rasmussen, 2011, ICML, "[PILCO: A model-based and data-efficient approach to policy search](http://link.zhihu.com/?target=http%3A//mlg.eng.cam.ac.uk/pub/pdf/DeiRas11.pdf)") 方法進行真實物理系統中的機器人控制。該文中，模型動態并不是一個神經網絡，而是一個相對比較簡單的高斯過程 (Gaussian Process, GP)。里面的方法本質上是 v2.0 版的框架，只是中間的 被確定為高斯過程。 1. 運行某種基本策略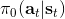（如隨機策略）來收集樣本數據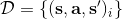。 2. **通過最大化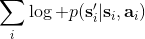的方法來學習模型動態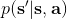。** 3. **通過**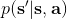**，使用反向傳播的方法來優化策略函數**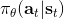**。** 4. 執行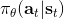，將新的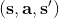加入到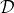中。反復執行 2-4 步。 其中最難的一點是第三步，在這里針對 GP 模型有比較特定的方法，但是大意對其他模型也是適用的。假設初始分布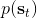已經給定為高斯分布，我們可以用當前學到的模型動態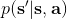來計算分布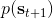。初始分布如果沒有給定，可以使用一些擬合高斯分布的手段。現在我們已經有了一個策略函數，也有了轉移分布（模型動態），我們可以將其復合，然后求其邊緣分布得到下一個階段的分布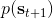。如此這般，反復得到之后每個階段的分布，然后使用這些邊緣分布來求期望收益，再求解這個期望收益關于策略函數中參數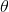的梯度。具體來看，如果邊緣分布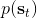是一個高斯分布，那么如果我們的系統被認為是一個高斯過程的話，我們可以得到下一階段狀態的邊緣分布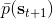的積分表達式，但這個分布通常不是一個高斯分布（可以是混合高斯）：因此我們采用矩方法（匹配前兩階矩）將邊緣分布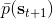投影到高斯分布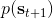上，作為一個近似。（_ 具體表達式請參見論文，RSS 和 ICML 兩篇都有 _）對于每一階段，我們都使用其邊緣分布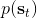來對收益求期望，最后總的期望收益就是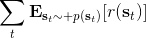，如果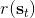性質較好（一般收益函數的采用都會去限制在一個比較好求解的范圍內，以方便求解）且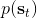是一個高斯分布的話，那么實際上這個期望是容易求的，對其使用鏈式法則求導即可（_ 收益是與均值、方差有關的，而均值、方差是和策略參數有關的，因此使用鏈式法則求導 _）。 Deisenroth et al. (2011) 使用這個方法去控制廉價的機械臂（攝像頭 130 美元，機械臂 370 美元），來堆疊彩色立方體塊。狀態是立方體塊的蹤跡，行動是對機械臂的致動。在視頻中，機械臂有 4 個關節的自由度，代價函數使得立方體塊盡可能接近目標；學習實驗次數很少，只用幾十次。方法很簡單，但是在實際問題中還是處理得很好。 在基于模型的增強學習中，我們非常關注的一點是我們應該用什么樣的模型簇，這其實是一個權衡的問題。 * 和上一個例子一樣，我們可以使用諸如**高斯過程**這樣非常有效的貝葉斯方法。如果我們使用高斯過程，輸入是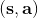，輸出是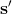；優勢在于，高斯過程和其他非參數貝葉斯模型的數據效率很高，這是因為它們可以在先驗知識和現有證據之間做出取舍，以抵抗過擬合或者數據不足 (low-data regime)：這對于基于模型的增強學習是很重要的，因為這種學習的速度取決于前期訓練得有多好，而前期訓練通常是數據不足的，如果前期嚴重過擬合了，就很容易卡住，后期也很難進行推進；缺點在于，高斯過程對于非光滑的系統動態效果不佳，而且對于數據大的情況下這個計算就會非常慢，訓練是關于數據量立方級增長的，而神經網絡則快很多。 * 第二個選項是使用諸如**神經網絡**這樣非常強大的參數模型，輸入是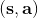，輸出是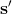。如果用一個歐氏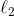（）損失函數的話相當于訓練一個高斯分布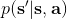的均值，也可以使用更復雜的損失函數，處理多峰問題（見[第二篇](https://zhuanlan.zhihu.com/p/32575824)），或者選擇除了高斯分布外更具表達能力的分布。它的優點不言自明，模型表現力非常強，而且非常擅長使用大量的數據，也適合推廣到高維系統；它的缺點在于在數據不足的時候表現不佳，因此在基于模型的增強學習中使用神經網絡要倍加小心，因為在早期訓練中可能會做出非常詭異的舉動。 * 其他選項譬如高斯混合模型 (Gaussian Mixture Model, GMM)，在機器人學中用得挺多的。它用很多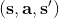元組來訓練 GMM，使用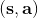來確定是在狀態行動聯合空間中的哪一塊，然后再確定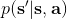。如果相信模型是譬如分段線性的，那么這樣的混合線性模型可能比較適用。（_ 這塊我自己不是很熟悉，請大家多指教 _）同樣也有很多其他特定領域的模型，如果你對你的系統比較了解，就可以寫出一些方程，然后去學習那些未知參數，通常表現很好。 * 其他能做的事情譬如說給定視頻的一幀，來預測某行動后的之后幀會是什么，這種高維預測問題在之后會涉及。 Nagabandi et al. (2017) 最近的"[Neural Network Dynamics for Model-Based Deep Reinforcement Learning with Model-Free Fine-Tuning](http://link.zhihu.com/?target=https%3A//arxiv.org/abs/1708.02596)"一文中使用了 v1.5 版本的框架（同時使用了一些無模型的方法來進行微調）來進行模擬機器人控制。這里基于的模型是神經網絡，而第三步的行動規劃只是做較短期的的隨機采樣（隨機采樣多條行動軌跡，然后選取最好的一條）。這樣做的原因是對神經網絡數據不足時的過擬合傾向進行補償，只進行短期規劃使得錯誤不會積累太多；同時進行 MPC 重新規劃，最佳路徑只選取第一步行動。如果模型預測錯誤，也問題不大，可以重新規劃。在不同種類機器人沿著檢查點一步一步走的問題中，機器人移動速度不算很快，但是方案相對比較靈活，適應各種檢查點的擺放軌跡。在 OpenAI Gym 的游泳項目中（游泳前進提高速度），如此基于模型的方法可以用很少的數據點（12k 個）完成無模型方法需要很多數據點（4m-11m 個）才能達到的目標，即便可能游得沒有無模型方法那么快，但至少樣本效率很高。基于模型的方法樣本效率很高，但是漸進偏倚很大，因為最后動作精度都受限于模型。基于模型的方法使用 12k 個樣本點達到收益函數 900，而無模型的方法通過 4m-12m 個樣本點達到收益函數 4800；這個例子清晰地告訴我們兩者區別原因在于**基于模型的方法嘗試的是提高模型擬合程度（需要的樣本數可能只是無模型的百分之一、千分之一），而無模型的方法則是去提高收益函數。** ## 從全局模型到局部模型 從最開始到現在，我們討論的模型幾乎都是**全局模型** (global models)，也就是說，我們學習一個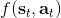，對于整個系統中都起作用。出于這個目的，我們嘗試使用單一的函數去擬合，譬如一個巨大的神經網絡。它對于我們所能訪問到的狀態行動處表現不俗，也可以用它來進行很好的決策。在我們的 v1.0 版框架中，問題在于如果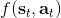一開始估計不好，那么規劃步就會去探索因為模型錯誤而被樂觀估計的區域（模型指向了錯誤的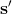，恰好比較優秀，規劃器以為會訪問到，而實際不會）。譬如說對于一個只會行走的生物，模型卻認為它下一步能飛起來，那么規劃器會嘗試去規劃它下一步怎么飛，而事實上它并不能飛。（_Levine 教授的題外話是如果在編寫一個物理模擬器的話，調試過程中不妨嘗試使用一些增強學習算法，能幫助我們了解怎么樣的行動會導致這個模擬器出 bug。如早期版本的 MuJoCo 有很多 bug，可能會使只能在地上爬的機器人站起來甚至飛起來，只是優化算法能弄清如何在這里面作弊。_） 要把一個模型學習得很好其實是壓力山大的，我們需要弄出一個很好的模型，在狀態空間的絕大多數區域都收斂到一個很好的解。有些時候我們可以使用較短的規劃期、MPC 等手段，但總體來說還是問題很大的。**在某些任務中，模型比行動策略要復雜很多**。譬如把一個有柄的杯子拿起來，我們的策略很簡單，拿住杯柄握起來放到對應位置就行，跟各種物理關系不大；而這樣一個問題的物理模型則非常復雜，如手可能是軟的會變形，接觸點可能很多，等等。因此將這些東西全盤考慮進來進行準確預測會很難。 相較于訓練很好的全局模型，有一些我們可以做的事情，譬如訓練**局部模型** (local models)。在我們之前所述的方法中，做軌跡優化通常需要的僅僅是模型在某點的導數，而這正是局部信息。因此，我們某種程度上也可以認為不見得一定要訓練好一個全局模型才能做好優化問題，而訓練一些能對梯度等局部信息有表征的模型也可以：事實上這個就簡單很多了。 現在我們只來關心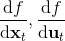。知道了這些信息之后，我們就可以用 iLQR 等方法來進行軌跡優化了。因此，我們的想法不是去擬合模型動態，而僅僅是去擬合關于當前軌跡或者策略的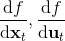，譬如使用線性回歸的方法。注意到 LQR 很好的特性是它是線性的，而且這個策略是可以在真實環境中運行的。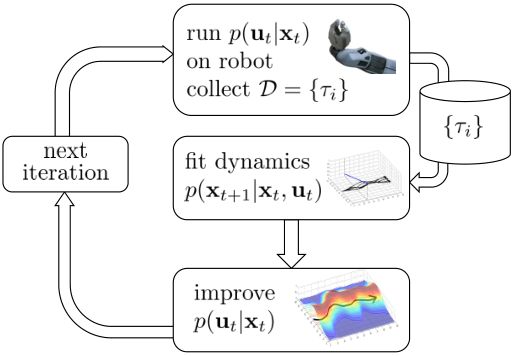  我們嘗試對一個增強學習過程進行拆解（_ 注：這邊圖里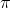也變成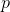了，但我還是嘗試把它區分開 _）。首先我們通過運行策略函數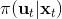，來收集軌跡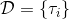。然后我們擬合模型動態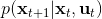：為了簡單起見，我們假設模型動態是一個高斯分布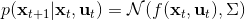，均值可能是比較復雜的非線性函數，然后有一個方差，基本上比較確定但是稍微有一些噪音。這個假設對連續系統還是比較合理的。我們假設在每個時刻，都有一個線性化表達式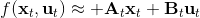，對于不同時刻矩陣是不同的。這樣近似其實已經很有表達力了，因為在不同的時間，前面的系數矩陣可能完全不同，但在給定時間下只是線性而已。這樣近似更是因為我們通常只會用到的一階導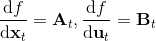，：因此如果我們能擬合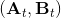，那么我們就能得到這兩個微分結果。從而，我們可以用這個來使用 iLQR 方法改進我們的策略函數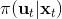，然后重新下一個循環。 在這個大框架下，其實有很多值得探討的問題。第一個問題是，**使用怎樣的策略**（這里也是控制器 controller）**去收集數據**。我們現在不嘗試去擬合一個全局模型了，所以選用怎么樣的策略的重要性就更強了。如果我們只是隨便選策略的話，那么我們很難去擬合當前策略下的局部信息。回顧 iLQR，執行完畢以后可以得到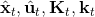，然后最優控制策略是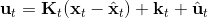。一個非常簡單的選擇（v0.5 版）是直接把 iLQR 的選取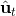作為錨點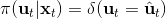，，當在行動中有偏差或者漂移的時候就會出問題。進一步我們選擇 iLQR 給出的最優控制（v1.0 版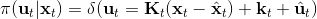），，看起來這樣的確定性策略有點兒“太好了”，如果我們想擬合局部信息，可能總是采取某種意義上的最優策略并不好，可能會總是往一個地方不停鉆，使用基本一樣的數據去擬合會使局部信息非常病態。一個更好的版本（v2.0 版）執行高斯分布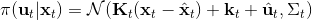：，其中均值是 iLQR 做出的最優控制，并**加入了一些噪音，使得數據不總是基本一樣**，數據多樣性稍微加強。在方差的選擇上可能需要注意，因為我們想得到不同的軌跡，但也不是徹底不同：這樣我們嘗試的就是去擬合全局模型而不是局部模型了，但這樣的線性化模型對全局模型的效果是很差的。 一個比較建議的方差是設置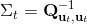。這個原因是代表了我們從狀態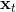執行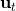后直到最后的最小代價的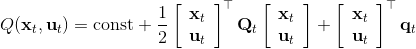，而如果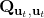很大的話，變動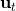對 Q 值影響就很大：如果變動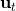對 Q 值很敏感，那么我們就不要變動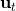很多；反之，它對噪音的承受力就強，我們可以選擇噪音的余地就大。我們加入噪音并不想很去干擾 Q 值，因此我們更愿意去加入一些對 Q 影響較小的噪音。相較于我們之前提到的 LQR 是去優化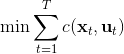，有一個有趣的結論是，使用 v2.0 方法我們事實上是在最小化一個有定義的目標函數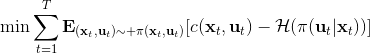：，也就是期望代價減去熵。其中熵函數定義為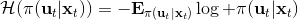。這樣的目標其實是試圖去找到噪音最大并且代價最小的的策略（雙目標規劃），也就是使策略盡可能隨機，同時保持一個低代價（高收益）：我們去學習一個局部模型，想做的恰好是這樣的事情。這樣的解又被稱為**最大熵** (maximum entropy) 解。 第二個問題是如何去**擬合這個局部模型**。假設我們已經收集了一些軌跡轉移數據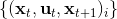。我們使用高斯分布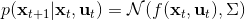的模型動態，因為我們在上一篇中已經提到過對于這樣的問題直接做 LQR 還是能得到最優解，我們可以忽略噪音的影響。最簡單的擬合方法是我們直接使用線性回歸，譬如假定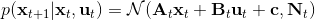（可以有個截距項）。一種更好的做法是考慮到在相近的時間點，模型動態可能是比較接近的，因此貝葉斯線性回歸（[一個很細致的講解在這里](http://link.zhihu.com/?target=http%3A//blog.csdn.net/daunxx/article/details/51725086)）可能是一個比較好的選擇，可以使用某些全局模型作為先驗分布：我們可以把所有數據用來擬合一個全局模型，并把它作為先驗，這樣可以提高數據的使用率。這樣的想法比較像是我們有一個全局模型，效果還可以但是不夠完善，由此我們把它作為先驗來提高局部模型的擬合。 當然，學習全局難度的模型需求量遠比局部模型高，因為局部模型的矩陣形式比諸如神經網絡全局模型簡單很多，但是局部模型的難點在于每次策略更新之后，局部模型就得推倒重來，以收集更好的樣本（也可以說是在線 (on-policy) 的基于模型的增強學習）：兩者是有權衡的，在一個盈虧平衡點后可能學習全局模型的代價相對更小了。具體代價和具體問題緊密相關，有些問題很容易去擬合全局模型，但是有些問題則很難。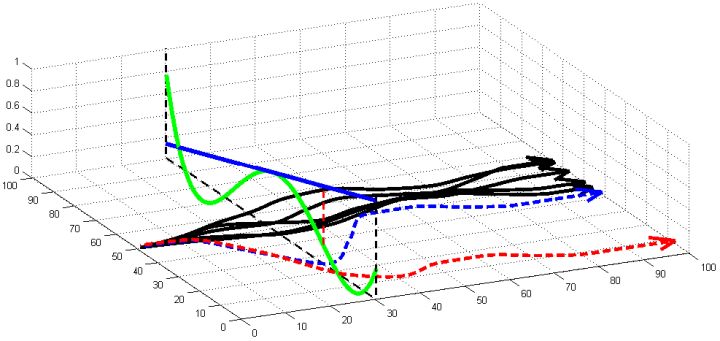  第三個問題是，我們更新策略函數總是希望讓它能與現在有所不同，那么**如果策略函數變化太大會怎么樣**？在上圖中，真實模型是綠色線的非線性函數，我們使用一個藍色線的線性模型去擬合（因此在中部一點相切）。我們進行一步更新的時候，可能到達一個比較遠的位置（紅色豎虛線投影），此時藍色擬合模型和綠色真實模型有很大的差別。在藍色線性模型下，我們認為軌跡只會是藍色的虛線；而我們實際運行時，由于藍色擬合模型完全是錯誤的，實際上我們拐到了紅色虛線這樣很遠的地方，就完全在計劃之外了。我們之所以叫藍色模型為局部模型，是因為它只能告訴我們在局部范圍內如何改進策略，而如果我們策略變動過大，則這樣不見得是一個改進（甚至可能是完全錯誤的），因為我們的局部模型太只關注局部了。我們要做的事情，是去限制每次迭代中，策略函數改變了多少，使得每一步走得不遠。 那么我們怎么做才能使得新的策略與原策略接近呢？我們的策略函數是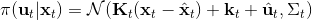，那么根據 Markov 性，一個軌跡的發生是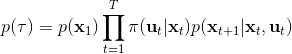。如果我們的新的軌跡分布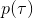和老的軌跡分布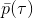比較相近，那么模型動態也會比較接近。[KL 散度](http://link.zhihu.com/?target=https%3A//en.wikipedia.org/wiki/Kullback%25E2%2580%2593Leibler_divergence)是一個描述兩個分布之間差異度的常見度量標準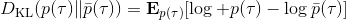，。從而，我們在更新策略的時候，如果加入一個限制條件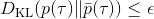，就能保證兩個策略下軌跡分布的差異能被控制在一個局部之內。順便一提，使用 KL 散度來控制軌跡分布差異的想法在除此之外的很多其他無模型的增強學習算法（如 TRPO）中也有應用。 現在我們來對 KL 散度的具體形式進行一些推導。因為兩個軌跡分布的初始分布和模型動態是一樣的，只有策略函數有所區別，因此現在有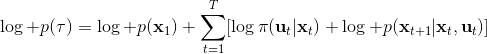和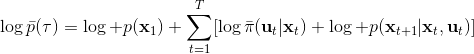。有點類似于策略梯度法，它們相減以后很多項也可以消去，得到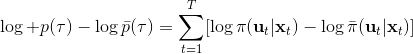，從而 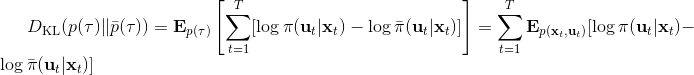。將前一項進行重寫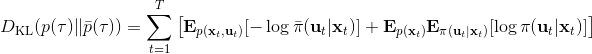，，然而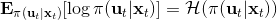。因此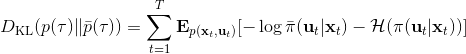，。回顧我們剛才使用加入高斯噪音的 v2.0 版本策略函數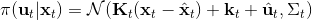是去優化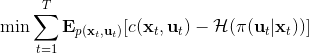的，因此如果我們能把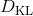搞到目標函數里面，那么我們就能用 iLQR 作為均值加上隨機高斯噪音來優化這個問題。 一般我們會采用拉格朗日乘子法來把約束放到目標函數里面。一個對偶梯度下降法（Dual Gradient Descent，DGD，其實在這里是上升）是這么做的：考慮問題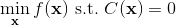，則拉格朗日函數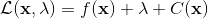，因此對偶問題為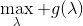，其中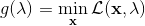（_ 假設強對偶，感覺意思是不強對偶的話也強行這么做先 _），從而通過優化對偶變量的方式，最優對偶變量下的優化問題正是原始問題的解。假設在給定拉格朗日乘子下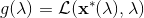，，對其求導得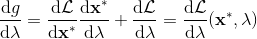，這是因為一階最優性條件保證了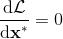。因此對偶梯度法做循環迭代以下三步： 1. 在給定拉格朗日乘子下，求解最優的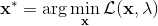。 2. 求解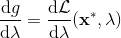。 3. 拉格朗日乘子走一個梯度步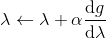。 這里面最難實現的應該是第一步。我們要用 DGD 方法來求解之前所說的約束下問題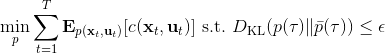。其中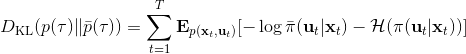，。那么它的拉格朗日函數是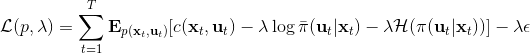，現在給定拉格朗日乘子下，要去最小化這個函數，求出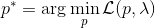。后面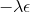是常數項先扔掉，然后把整個式子除掉（不嚴格地，假設乘子不為 0），那么原優化問題和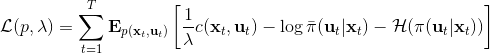同解。那么我們只需要構造一個新的代價函數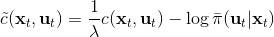，然后執行 LQR，加入高斯噪音就可以了。迭代執行以下步驟： 1. 構造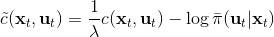，并使用 LQR 加入高斯噪音的方法得到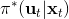。 2. 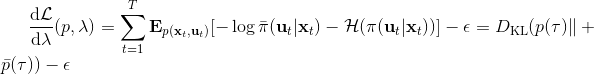，更新乘子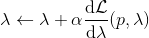。 控制兩個策略間的 KL 散度在很多場合下都是非常有意義的（譬如在無模型增強學習中也存在采樣的誤差），而且控制兩個策略間的 KL 散度等價于控制軌跡分布之間的 KL 散度。 Levine et al. (2015) 發表在 ICRA 上的"[Learning Contact-Rich Manipulation Skills with Guided Policy Search](http://link.zhihu.com/?target=https%3A//arxiv.org/abs/1501.05611)"一文闡述了使用局部模型，使用 KL 散度信賴域，結合 iLQR 進行規劃來控制機器人的應用。機器人學習堆疊樂高塊（插入動作），通過旋轉機械臂來擬合模型動態，每收集一些（10 條）軌跡就停下來幾秒用來更新局部模型，并更新策略函數。機械臂在反復試驗后，逐漸傾向于完成插入樂高塊的任務。這個工作并不訓練神經網絡，只是做局部的線性模型擬合來研究怎么去做這個任務。高斯噪聲使得機器人傾向于進行一些探索。 Fu et al. (2016) 的發表在 IROS 上的"[One-shot learning of manipulation skills with online dynamics adaptation and neural network priors](http://link.zhihu.com/?target=http%3A//rll.berkeley.edu/iros2016onlinecontrol/online_control.pdf)"一文將全局模型和局部模型結合起來，使用全局模型做先驗，進行貝葉斯回歸來訓練局部模型，來控制機器人完成任務。特別的是，機器人使用過去的經驗來完成新的任務（任務不同，但有相似結構）。機器人使用過去的經驗來訓練一個全局模型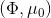，然后接受新任務的很多軌跡信息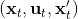，在線訓練一個經驗估計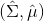，從而得到后驗局部模型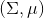，做 MPC 每一步重新規劃。在視頻中可以看到，因為在線學習，所以在試驗過程中一邊就把局部模型給學習了，逐漸適應任務以提高執行水平。