# (10) 基于模型的增強學習的策略訓練 > 作者：[謝天](https://www.zhihu.com/people/xie-tian-55-77) > > 來源：[POST 館](https://zhuanlan.zhihu.com/c_150977189) ## 使用基于模型的增強學習訓練策略 在上兩篇中，我們對基于模型的深度學習進行了大致的探討，包括如果我們已知模型信息如何進行利用來做出正確的決策（如 MCTS 和 iLQR），在不知道確切模型的情況下如何收集數據學習模型。其中在上一篇中，我們給出了收集數據學習模型的框架，并使用 iLQR（包括加入噪聲成為 Linear-Gaussian）進行規劃；我們分別探討了如何訓練全局模型（如高斯過程 GP，神經網絡等）、如何通過控制舊軌跡和新軌跡的 KL 散度的方法在一個信賴域中訓練局部模型（如線性模型），也可以用諸如貝葉斯回歸的方法將全局模型作為先驗更好地訓練局部模型。在訓練模型之外，我們討論的控制基本上局限于 v1.5 版本以下的在線執行某些規劃過程，主要是 v1.5 版本的閉環 MPC 方法，是具有相當的魯棒性的。 在這一篇中，我們將探討通過基于模型的增強學習算法來訓練策略，如何像 v2.0 版本一樣使用策略來做決策。獲得一個策略有很多好處，首先使用策略來進行在線行動選擇是一個輕量級的方法，遠比 v1.5 的每步在線重新使用規劃方法求解快；此外更重要的是，**訓練策略可能有比訓練模型有更好的泛化能力**（但不一定，取決于問題）。舉個例子，考慮到（譬如在棒壘球中）我們去接一個球，基于模型的算法考慮物體的飛行軌跡，譬如如何受重力和風力影響，然后求解運動問題，確定落地點，然后過去接球；而事實上人類去解這個問題更簡單，如我們只需要追趕這個球，保持一定的速度使得球在視野里面就行了，我們沒必要關注具體的物理動態，也能接住這個球。這個例子說明了有可能使用策略的話，觀測和行動之間會是一個比較簡單的關系，從而訓練一個不錯的策略比搞清楚模型具體是什么更容易泛化，更容易提煉出某種意義上的“知識”作為策略以適應新情況：人類的接球策略可以在物體不是球的時候也通用，而根據物理模型規劃計算則需要做很大變化了。  我們繼續祭出之前多次使用過的計算圖。這個計算圖本質上體現了**策略函數**和**模型動態**影響**代價（收益）**的形式（包含了三個重要組成部分，注意這里換成最小化代價了，其實是一樣的）。在 v2.0 版框架中，我們考慮使用反向傳播的方法來優化策略函數**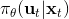**：如果這三個東西都是可微的，那么我們就可以求出代價關于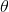的梯度（對于確定性策略更容易，對于有些隨機策略也是可行的，如之前所講的[PILCO 方法](https://link.zhihu.com/?target=http%3A//mlg.eng.cam.ac.uk/pub/pdf/DeiRas11.pdf)匹配前兩階矩），從而反向傳播是可以做到的。但不幸的是，直接這樣簡單的做法通常并不可行。  考慮最早期的行動，最早期的行動通常對整個軌跡有非常大的影響（如上圖，第一個動作變化可能會使得整條軌跡有很大的晃動），可能會影響所有后續的狀態和動作，因此關于它的梯度應該是非常大的；而在后期的行動，在整個序貫決策問題中關于總代價起到的作用就比較小了，因此關于它的梯度就小：從而，這個梯度會相當病態。這個**參數敏感問題**在射擊法 (shooting method) 中也同樣存在，在射擊法中我們同樣也不使用一階算法而使用類似 LQR 的二階算法，但是在這里我們就不再有一個類似 LQR 的容易的二階方法來求解這個問題了：因為引入了含參的復雜的策略函數，這些參數在整個問題中將非常糾結，因此不再能用簡單的動態規劃方法求解了；我們會發現，其實這樣的求解序貫問題和訓練 RNN 非常相似，而訓練 RNN 的一個重要方法就是 BPTT：因此，訓練這個問題所遇到的問題和 BPTT 中**梯度爆炸/消失的問題**本質上非常相似，但是 RNN 我們可以通過選擇類似 LSTM 的表達結構來使得梯度變好，而對于我們的問題來說，系統動態是外生的客觀存在的，我們只能去學習而并不能自主選擇。因此我們遇到的問題相對來說更棘手。 ## 引導策略搜索 (GPS) 相比射擊法，搭配法 (collocation methods) 優化每個時刻的狀態或者同時優化狀態和行動，并使用約束來表示狀態轉移的關系。這樣的方法相對射擊法而言，就沒有那么參數敏感了，但是困難在于它不是一個無約束優化問題了。有一個特點是，我們可以將策略**引入優化問題中，作為約束條件**，而不再成為射擊法一樣的計算圖的一環，便有了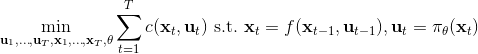（這里先假設都是確定性的）。這個表達形式還是同時優化狀態和行動的，也可以只去優化狀態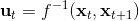，，這樣行動就是相鄰兩個狀態的產物。 為了讓這個問題容易求解，我們可以先把這個問題分離出來，一方面去優化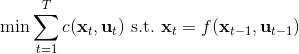，這是普通的軌跡優化問題，可以用之前講過的 LQR 等方法進行優化；同時又施以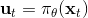的約束。為了求解這樣的問題，我們使用增廣拉格朗日乘子法 (augmented Lagrangian method)，非常類似于上一篇中的 DGD 算法，只是求解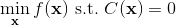問題時，拉格朗日函數變成了增廣拉格朗日函數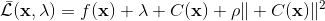，加了一個二次懲罰項，使得在嚴重違反約束條件時更傾向于控制約束條件以增加穩定性（這個函數最常見在 ADMM 算法中被涉及到，這個算法也算是 ADMM 的一個特例）。增廣拉格朗日算法的總體框架還是和之前一樣，迭代進行以下步驟： 1. 在給定拉格朗日乘子下，求解最優的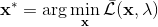。 2. 求解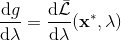。 3. 拉格朗日乘子走一個梯度步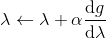。 我們記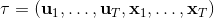，則優化問題可以簡寫為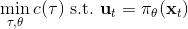。它的增廣拉格朗日函數可以寫成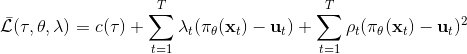。這個函數有兩塊未知參數和一塊乘子，因此考慮形式上非常接近于 ADMM 的這樣一個算法： 1. 固定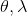，使用諸如 iLQR 的方法優化軌跡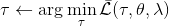。 2. 固定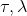，使用諸如 SGD 的方法優化策略參數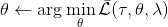。 3. 拉格朗因為日乘子走一個梯度步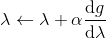。 其中第一步相當于重新構建一個代價函數，把后面部分包進去，然后執行 iLQR。第二步注意到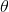只和后兩項有關，而后兩項的形式簡單，且能完全按時間分解：這樣的好處是不需要再做反向傳播了，而稍作變形，本質上只是一個非常傳統的最小二乘監督學習問題，可以用一些 SGD 方法進行求解。因此整個過程是交替使用軌跡優化和監督學習，不需要再做 BPTT。這樣的方法理論上需要凸性，但是如果沒有凸性的話有些時候實踐中效果也還可以。當然，要讓這樣的算法在實際中可用，還需要做一些其他工作。 這樣的算法屬于**引導策略搜索** (Guided Policy Search, GPS)，這樣的叫法主要因為策略訓練是跟著軌跡優化的結果而來的。有意思的是，該算法一方面可以被理解成在**約束下的軌跡優化算法**，同時因為第二步就是一個監督學習過程，另一方面可以被理解成**對最優控制的模仿學習**。這也建立起了基于模型的增強學習與模仿學習之間的關系。最優控制扮演了老師的角色，同時最優控制又需要去適應學習者（因為第一步軌跡優化是與給定策略有關的），避免一些學習者不能模仿的行動，屬于一種自適應學習。廣義的 GPS 算法的一般結構是這樣的： 1. 關于某些修改后的代價函數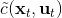進行軌跡分布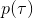的優化。 2. 關于某些監督學習的目標函數優化策略參數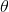。 3. 修改對偶變量。 本質上只是之前算法的推廣泛化，第一步修改代價函數以加入增廣拉格朗日函數的兩項，第二步不需要考慮原始代價函數因為原始代價函數只與軌跡有關，而與策略參數無關。我們需要選擇的是**軌跡分布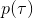的形式**（或者干脆確定性的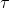，確定性形式比較容易，而隨機形式一般需要使用比較簡單的分布類如高斯分布去近似）、**分布**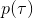**或者**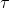**的優化算法**（第一步的軌跡優化算法）、**修改后的代價函數**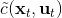、**用來訓練**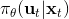**監督學習的目標函數**。舉例來說，確定性形式其他部分就跟我們剛才所說一致，問題為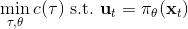，我們的第一步中修改的目標函數就是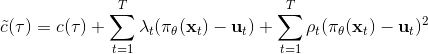 。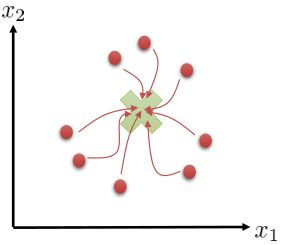  我們有時候也會遇到需要從多條軌跡中學習策略的問題。以上圖為例，我們從小紅點出發，想走到小綠叉位置。然而從一個點出發的路徑容易規劃，但是這樣一條單一的路徑可能對策略學習不太好，所以我們想從多個不同的出發點開始學習策略以提高策略的泛化能力。這樣的問題又可以被表述為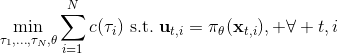，同時優化一組軌跡，減少它們的共同代價，并將它們限制在同一策略之下。這個時候 GPS 算法的第一步只需要改成對所有的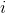，關于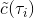進行軌跡優化：這一步其實可以并行完成，因為它們只與被固定下來的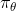有關，而互相之間其實沒有聯系。第二步需要把這些數據全部拿過來放在一起進行監督學習。Mordatch et al. (2015) 發表在 NIPS 上的文章"[Interactive Control of Diverse Complex Characters with Neural Networks](https://link.zhihu.com/?target=http%3A//papers.nips.cc/paper/5764-interactive-control-of-diverse-complex-characters-with-neural-networks)"就利用了這一并行（在多臺機器上訓練，然后合起來）的約束下的軌跡優化的方法來訓練神經網絡策略，在 MuJoCo 模擬器上完成了復雜生物（如類似蝙蝠翅膀，更復雜的如人形機器人的步態）的運動 (locomotion) 學習，可以做到向某一目標移動的實時控制。在訓練策略之外，這樣的介入策略的做法還提高了軌跡優化本身：策略的介入迫使行動成為狀態的函數，使得軌跡優化會做出**周期性的穩定控制**，而不僅僅是一個不穩定的只為了到達目標的控制。在這里，不同的軌跡意味著不同的起點和終點。 對于隨機 GPS 問題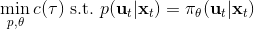，控制器從單一策略變成了一個策略分布。我們僅以最簡單的（局部）線性均值加高斯噪音的控制器為例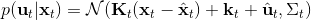，，這類形式比較容易求解。第一步優化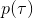，目標函數我們上一篇中在一個信賴域中擬合局部模型相似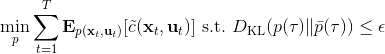，。使用這樣的方法訓練策略，相當于在原來的結構上多出一塊訓練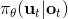的部分。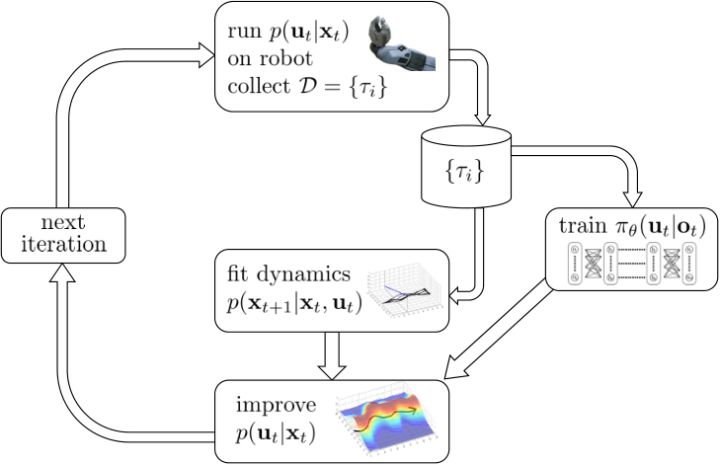  首先第一步使用我們現在的線性-高斯控制器來運行機器人，以收集一些軌跡樣本；第二步去用這堆軌跡去擬合模型動態（一些回歸的方法），然后在信賴域中更新線性-高斯控制器。在信賴域中找新控制器的時候，我們同時使用上了用這堆軌跡數據訓練的神經網絡策略。在機器人學的背景下，Levine et al. (2016) 等人投稿于 JMLR 的"[End-to-End Training of Deep Visuomotor Policies](https://link.zhihu.com/?target=https%3A//arxiv.org/abs/1504.00702)"一文提供了一種端到端的策略訓練機器人做事情的方法。此時我們的神經網絡不再訓練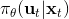，而改為訓練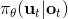，也就是以機器人的視覺圖像為一段，輸出直接為策略函數，這樣的端到端學習，下圖即為端到端的 CNN 結構。  因此我們的 GPS 問題變為了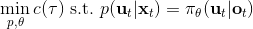。我們使用局部模型進行（低維度的）軌跡優化作為老師來得到策略，但是我們在真正訓練神經網絡的時候則把輸入替換為機器人看到的圖像，然后進行監督學習，重復這個過程。在訓練神經網絡時候我們把輸入從狀態偷偷替換成了原始圖像，這樣的技巧叫做**輸入重映射** (input remapping trick)：在軌跡優化的時候我們采用狀態，而在訓練策略的時候我們使用圖像，這種方法有助于我們訓練從**傳感器（如攝像機）直接得到的高維輸入的策略**。比如說在移動方塊的任務中，在訓練的時候，機器人可能可以通過某種方法知道木塊在哪里（也就是知道狀態是什么），但是在測試的時候則只能通過圖像來確定策略，這樣的方法就可以用上了。 ## PLATO 算法 在這一塊，我們介紹另一種使用模仿學習的方法。這個想法是基于之前我們提到的約束下的軌跡優化問題又可以理解為一種對最優控制的模仿學習。那么說到[模仿學習](https://zhuanlan.zhihu.com/p/32575824)，那么算法就不只有一種了，在之前的模仿學習中我們就介紹過 DAgger 算法，一個模仿最優控制的應用就是[之前](https://zhuanlan.zhihu.com/p/33093879)提到過的 Guo et al. (2014) 使用 MCTS 來提供 Atari 游戲樣本，并使用 DAgger 算法來實現模仿學習 MCTS 策略。 最原始的 DAgger 存在一些問題。譬如該方法的第三步要求**人工標注新樣本**，這非常不自然的，因此我們使用某些如最優控制的方法**讓計算機自動標注這些新樣本**，算是得到了解決。DAgger 的另一個很大的問題是我們在一開始需要通過人工數據來訓練一個策略，然后**運行這個策略**來得到數據。但是這個策略在一開始可能是非常糟糕的，我們只有在反復增加數據之后才能緩解分布不匹配的問題，而分布不匹配問題在一開始非常嚴重，甚至是災難性的（如駕車）。如果我們能用一些基于模型的增強學習算法來“更好地”運行這些策略，使得安全系數提高，那么不失為一件好事。 Kahn et al. (2016) 在"[PLATO: Policy Learning using Adaptive Trajectory Optimization](https://link.zhihu.com/?target=https%3A//arxiv.org/abs/1603.00622)"提出的 PLATO 算法正為解決這個問題而存在。該算法將 MPC 思想引入到 DAgger 算法中，而 MPC 的每步重新規劃正是為了克服誤差的。DAgger 算法的第二步嘗試執行監督學習訓練出來的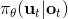來獲取數據集，就是我們學出來什么策略就運行什么策略，來克服分布不匹配問題；而事實上 PLATO 算法告訴我們，我們可以稍微做一點妥協，且同樣也能得到收斂性保證：我們嘗試使用一個近似的策略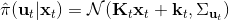，而這個策略出自使用 LQR 來求出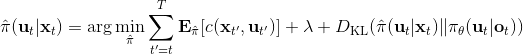，和之前一樣，結果是一個線性均值的高斯分布。譬如在駕車過程中，如果發生碰撞就會得到一個很高的代價，這樣的策略就會以降低代價函數為目標，同時也保證新策略不與就策略差別過大。我們在每一步中執行這樣的新策略作為校正，均衡長期代價和與當前策略的接近程度。注意到，我們的策略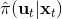在每一步最小化的是**長期的期望代價**和**當前階段的 KL 散度**（兩者的一種權衡），因此它實際想做到的是做出一個不背離當前階段策略太遠的長期期望代價最低的決策。因此，我們將該算法結合 MPC 進行使用，在每一步就需要重新規劃。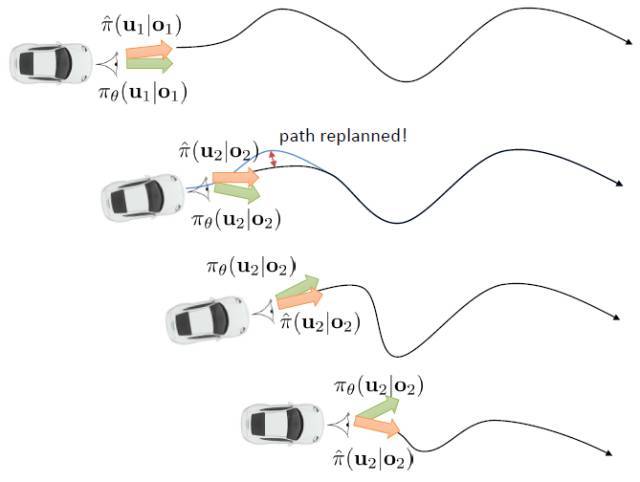  在這里，我們和前面 GPS 中所提到的一樣，使用了輸入重映射的技巧，控制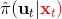和 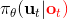之間的 KL 散度，這是因為我們學到的策略可能只是關于觀測到的圖像，而我們實際發生的控制策略則需要根據狀態得到。PLATO 算法想做到的是，在訓練階段，我們可以有一些外部的觀察者來給出車輛的狀態信息，使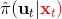相對來說比較聰明，以避免很多不必要的損失；但是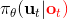還是要根據原始的傳感器等信息來學的，這個可能比較難學，但是我們在真實測試環境中還是要靠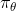。我們知道觀測是由狀態決定的，但是我們的模型是用來預測未來的狀態的，如果我們有模型的話我們可以知道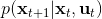，但是觀測的分布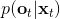是不知道且極難的：相對預測下一幀圖像而言，我們更容易弄清楚下一個狀態是什么。因此我們也不是對未來的觀測做規劃，而是對未來的狀態做規劃。我們知道下一階段的狀態是什么，但是不知道下一幀觀察是什么：因此我們執行一步操作后，我們就能得到下一階段的觀測，然后重新規劃，進行這樣的循環。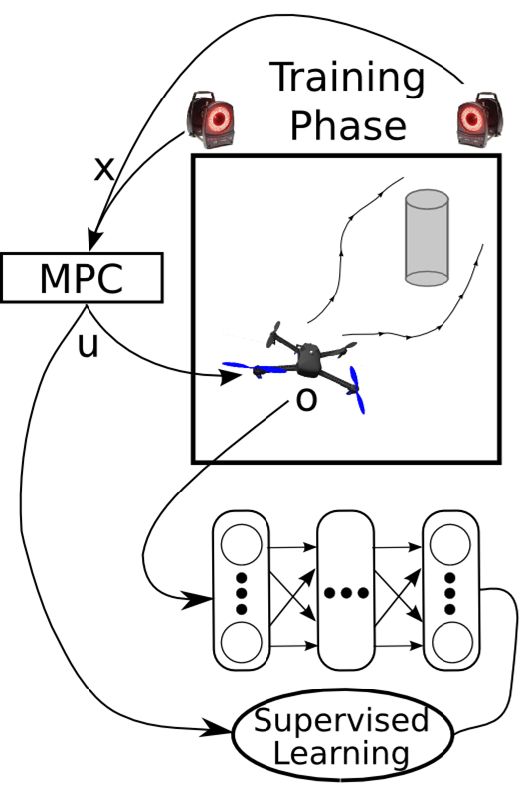  這樣一個訓練四旋翼躲避障礙物的任務中，在訓練過程中，四旋翼被監視器等設備所控制（或者使用激光測距儀等），因此它能很好地得到自己的狀態進行重新規劃，同時也使用輸入重映射技巧，端到端地訓練直接的從觀測到行動的策略；在實際測試中，則使用原始觀測圖像。總體來說，這種 DAgger 的變種算法中，我們代價函數中的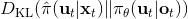使得我們能去學習改進策略，直到最后變成一個完全在線的行為，這意味著分布不匹配問題得到了解決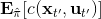；使得我們能避免高代價（如碰撞損毀），即便我們的策略和原始策略有差異，哪怕產生分布不匹配的問題，我們也不想產生太高的代價。 ## 一些總結 在本篇中，我們首先提到可以使用反向傳播的方法訓練策略，但是由于梯度爆炸/消失等問題效果不佳。接著我們通過將策略作為約束條件來進行搭配法的方式，使得基于模型的增強學習非常像對最優控制（軌跡優化等）的模仿學習，并具體講了 DAgger 類算法和 GPS 算法。DAgger 算法不需要一個能自適應策略變化的專家，因此如果我們有一個很難去修改目標函數等以適應策略的規劃算法的話，DAgger 是一個很好的選擇。但是 DAgger 也有自己的假定，它**假設我們的學習者可以學到一個策略，使得和專家行為之間的差距是可以被控制在一個很小的范圍之內的**，也就是說假設不存在學習者怎么都學不會的情形。事實上，這樣差距不可控的情形是存在的，如在部分觀測的問題中。一個極端的例子是在駕車時不給車任何觀測信息，也有可能我們的策略簇根本無法學會專家行為。而 GPS 算法則需要專家去適應學習者，也需要修改軌跡優化算法來加入策略的損失信息，但是正因如此，專家時刻跟著學習者走，它不需要控制差距的范圍。 我們之所以想去模仿最優控制，主要是因為這樣做相對比較穩定且好用：我們現在已經能把監督學習算法做得很好了，最優控制算法通常來說也效果不錯，因此兩者結合通常也可以期望能有不錯的結果。我們可以使用輸入重映射的技巧，在做最優控制時候使用低維度的狀態信息，而在訓練策略時候可以引入高維觀測信息。它也能克服直接做反向傳播方法的諸多困難。此外，這樣的做法通常樣本利用率高，且對于實際物理系統可行。 我們對迄今為止討論的兩大類基于模型的增強學習算法進行總結。第一類是不引入策略，光學習模型并使用模型進行規劃。這類方法迭代逐漸收集數據來克服分布不匹配的問題，同時我們也可以使用 MPC 的方法在每一步進行重新規劃來克服模型誤差帶來的影響。第二類更先進點的算法是引入并學習策略。當然我們可以使用反向傳播的方法來訓練策略函數，這類算法的代表是使用高斯過程匹配兩階矩的 PILCO，相對簡單但是不穩定。更通用的方法是模仿最優控制，可以像 GPS 一樣做約束下的最優化，也可以使用 DAgger 類的算法諸如 PLATO。還有一類沒有提及的方法是 Dyna 方法，是介于有模型方法和無模型方法之間的混合方法：大意如訓練一個模型（神經網絡）作為模擬器來生成樣本，但是使用無模型的方法進行學習。如果我們已經有了一個無模型的算法，但是苦于數據不足的話，是個不錯的選擇。 當然，基于模型的增強學習算法也有局限性。首先顧名思義，**我們必須要有某種模型**，但不見得總能得到某種模型：有的時候模型簡單，但有的時候就很復雜；而且有時候學好模型比學好策略更難（模型復雜但策略不復雜）。學習一個模型需要很多時間和數據，而且比無模型的方法求解計算代價更高。雖然基于模型的方法通常需要的數據量較少也能得到一個還可以的控制，但也取決于學習模型和策略哪個更容易。**速度和表達力通常需要有一個權衡**：有時候一個表達能力很強的模型（如神經網絡）速度很慢（取決于具體問題），有時候一個速度較快的模型（如線性模型）去處理非常復雜動態系統的表達力不夠。同時，基于模型的增強學習算法**需要引入很多額外的假設**，這在無模型算法中通常沒有。如需要認為（局部某種意義上的）可線性化或者連續，這個在很多真實物理系統還是可以的，但是對一些離散系統（如 Atari 游戲）就不適用了；尤其是對于線性局部模型，需要能夠重置系統以在同一狀態下多次嘗試，雖然有些無模型的方法也需要這個假設，但是通常在在線處理就夠好了；在有些模型（如 GP 類全局模型）中，需要假設光滑性，不能不可微；等等。 我們也對基于模型的方法和無模型的方法進行綜合比較。因為要進行增強學習，我們必須要收集數據，要么是在廉價的模擬器上，要么是在昂貴的真實物理系統，所以首先比較樣本效率。通常樣本效率最低的是**不基于梯度的算法**（如 NES (Natural Evolution Strategies)、CMA-ES 等），這類算法是無模型的算法，且不計算神經網絡的梯度，但依賴于隨機優化。**完全在線的算法**（如 A3C 算法）雖然比前者要好一些但是樣本效率還是較低，這類算法在線學習，不使用基于策略的回放緩沖池，依賴大規模的并行。**策略梯度法**（如 TRPO 等）的樣本效率較前者再進一步，雖然也是在線但是使用批量處理的方法提高效率。樣本效率更好一些是**基于回放緩沖池的值函數方法**（如 Q 學習、DDPG、NAF 等），這類方法是離線的。**基于模型的深度增強學習算法**（如 GPS）和**基于模型的“淺度”增強學習算法**（如 PILCO，不使用深度神經網絡）則遞進提高了樣本效率，但在這塊也意味著引入了越來越嚴格的假設。這邊差不多每一級基本上是樣本效率差了 10 倍。Salimans et al. (2017) 的"[Evolution Strategies as a Scalable Alternative to Reinforcement Learning](https://link.zhihu.com/?target=https%3A//arxiv.org/abs/1703.03864)"一文說明 cheetah 任務中進化算法樣本效率比完全在線的算法低十幾倍。Wang et al. (2017) 的"[Sample Efficient Actor-Critic with Experience Replay](https://link.zhihu.com/?target=https%3A//arxiv.org/abs/1611.01224)"一文訓練 A3C 算法約需一億步（完全真實時間 15 天）。Schulman et al. (2016) 使用 TRPO+GAE 方法約需一千萬步（完全真實時間 1.5 天），十倍的效率提升。Gu et al. (2016) 的"[Continuous Deep Q-Learning with Model-based Acceleration](https://link.zhihu.com/?target=https%3A//arxiv.org/abs/1603.00748)" 使用 DDPG 方法（完全真實時間 3 小時）達到十倍的效率提升，使用 NAF 完全真實時間 2.5 小時。到了基于模型的增強學習，計算的時間可能比數據收集時間更多，因此瓶頸重點轉移到了計算。Chebotar et al. (2017) 的"[Combining Model-Based and Model-Free Updates for Trajectory-Centric Reinforcement Learning](https://link.zhihu.com/?target=https%3A//arxiv.org/abs/1703.03078)"一文體現了對于真實控制問題 GPS 比 DDPG 有 10 倍的樣本效率提升。對于淺層方法，效率提升大約也是 10 倍，但是相對來說問題更簡單了。注意到有很多時候我們不能只看真實時間，模擬器可能非常快，因此如果我們能并行得到很多計算資源，那么可能樣本效率低的算法反而更快，都是一些權衡。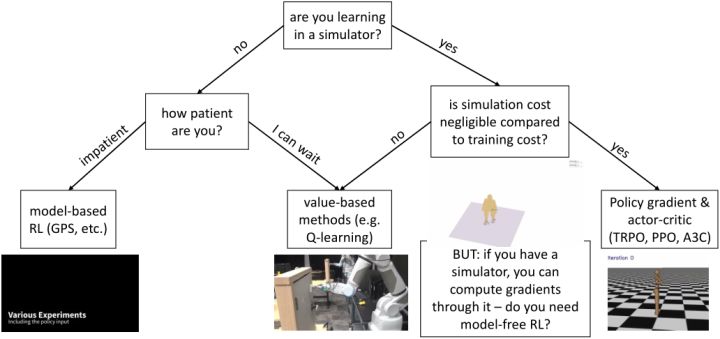  最后我們來討論如何根據問題選擇合適的增強學習算法。最重要的問題可能是我們是否是從模擬器中學習，因為這決定了算法樣本效率的重要性。如果是的話，我們要看模擬成本是不是相對訓練成本是可以忽略不計的（決定樣本效率有多不重要）：如果是，我們會考慮樣本效率較低的算法如策略梯度法 TRPO/PPO，和完全在線的算法如 A3C，這樣實際運行時間可能較少，而且如策略梯度法可能更容易調參；如果模擬成本不低，那么我們可能希望使用如 Q 學習/DDPG/NAF 的基于值函數的方法來提高樣本利用率。值得一提的是，如果使用模擬器，另一個問題是我們某種意義上可以用模擬器來算出梯度，哪怕不能直接得到也可以得到一個數值解（尤其是如果我們在求解連續問題）我們可能不是在需要無模型的算法，而是需要 MCTS 或者軌跡優化這樣的方法；也并不總是這樣，有時如策略梯度法的無模型方法可能比這些規劃算法要效果好，但無論如何是值得討論的。回到我們不使用模擬器的情形，此時樣本效率可能很重要，取決于我們有多少時間（或者能否自動收集數據，是否需要在工作時有人監督）。如果我們沒什么時間，那么可能會傾向于諸如 GPS 的基于模型的算法，此時對模型的選擇和假設很重要；如果我們時間還是很充裕的，那么可以使用可能更有效的值函數法。