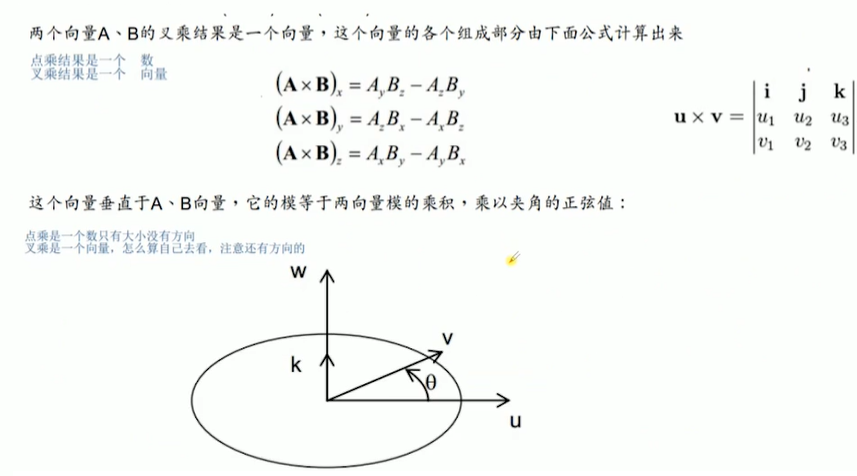
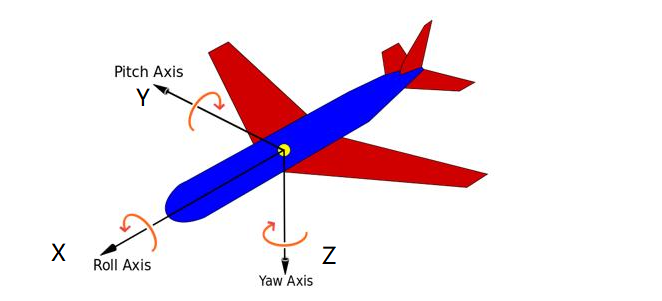
向量運算法則在后面的算法推倒中會用到。   飛控中使用的姿態表示法有：歐拉角、旋轉矩陣、四元數。 [TOC] # 1. 坐標系     姿態用來描述地球坐標系與機體坐標系之間的角關系，其姿態解算需要解決的是如何表示四旋翼與地球坐標系的相對姿態。所以在這里分別建立地球坐標系與機體坐標系，才能更清楚地描述它們之間的關系，如圖4-3。  定義兩個坐標系Z軸（上圖未畫出）的正方向為重力加速度g的方向，地球坐標系的原點為四旋翼起飛的地點，機體坐標系的原點為四旋翼重心位置。到這里坐標系就建立完成了。 # 2. 歐拉角     歐拉角的定義不僅僅和旋轉角度有關系，還和旋轉軸的旋轉順序有關系，任何一種旋轉順序都是合法的。根據定義，歐拉角有12種旋轉順序(維基)，一個物體通過任意一個旋轉順序都可以達到同樣的姿態，在各個學科里所以為了統一，航空航天領域規定XYZ為歐拉角的旋轉順序。     飛行器依次繞過不同的坐標軸連續轉動三次，即可實現從一個坐標系轉換到另一個坐標系，這三次轉動的角度為繞X軸旋轉得到的橫滾角Roll、繞Y軸旋轉得到的俯仰角Pitch，繞Z軸旋轉得到的偏航角Yaw，這三個角就是歐拉角。  # 3. 旋轉矩陣     在二維平面上，旋轉矩陣定義如下，它可以將`$ O^{'} $`的坐標用`$ O $`坐標來表示，從而實現坐標系的轉換。  從二維空間擴展到三維空間，就是讓二維旋轉矩陣分別繞 Z軸、Y軸、X軸（順序不能調換）進行旋轉，得到三個矩陣，將這三個矩陣相乘得到最終的旋轉矩陣。  旋轉矩陣簡化后的表達式如下：  # 4. 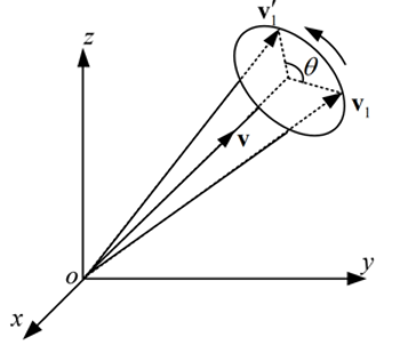四元數     四元數姿態表達式是一個四個參數的表達式。它的基本思想是：一個坐標系到另外一個坐標系的變換可以通過繞一個定義在參考系中的矢量`$ \overrightarrow{u} $`一次性轉動來實現。如下圖所示，將`$ \nu^{'}_{1} $`向量用`$ \nu_{1} $`向量進行表示，可以按式（4-1）來轉換： :-:  ```[tex] \begin{bmatrix} 0\\ \nu^{'}_{1} \end{bmatrix} = \overrightarrow{q} \bigotimes \begin{bmatrix} 0\\ \nu_{1} \end{bmatrix} \bigotimes \overrightarrow{q}^{-1}..................................................(4-1) ``` 其中`$ \overrightarrow{q} = \begin{bmatrix} cos\frac{\theta}{2} \\ \nu sin\frac{\theta}{2} \end{bmatrix} $`就是四元素。 四元素用矢量`$ \overrightarrow{q} $`來表示，四元數的表達方式共有5種，分別如下： **（1）矢量式** ```[tex] \overrightarrow{q}=q_{0}+\overrightarrow{q}_{u}..................................................(4-2) ``` `$ q_{0} $`為標量，`$ \overrightarrow{q}_{u} $`是三維空間的一個矢量。 **（2）復數式** ```[tex] \overrightarrow{q}=q_{0}+q_{1}\overrightarrow{i}+q_{2}\overrightarrow{j}+q_{3}\overrightarrow{k}..................................................(4-3) ``` 可視為一個超復數，`$ \overrightarrow{Q} $`的共軛復數記為： ```[tex] \overrightarrow{q}^{'}=q_{0}-q_{1}\overrightarrow{i}-q_{2}\overrightarrow{j}-q_{3}\overrightarrow{k}..................................................(4-4) ``` `$ \overrightarrow{q}^{'} $`為`$ \overrightarrow{q} $`的共軛四元數。 **（3）三角式** ```[tex] \overrightarrow{q} =cos \frac{\theta}{2}+\overrightarrow{u}sin \frac{\theta}{2}..................................................(4-5) ``` `$ \theta $`為實數，`$ \overrightarrow{u} $`為單位向量。 **（4）指數式** ```[tex] \overrightarrow{q} =e^{\overrightarrow{u}\frac{\theta}{2}}.................................................(4-6) ``` `$ \theta $`為實數，`$ \overrightarrow{u} $`為單位向量。 **（5）矩陣式** ```[tex] \overrightarrow{q} =\begin{bmatrix} q_{0}\\ q_{1}\\ q_{2}\\ q_{3} \end{bmatrix}.................................................(4-7) ``` # 5. 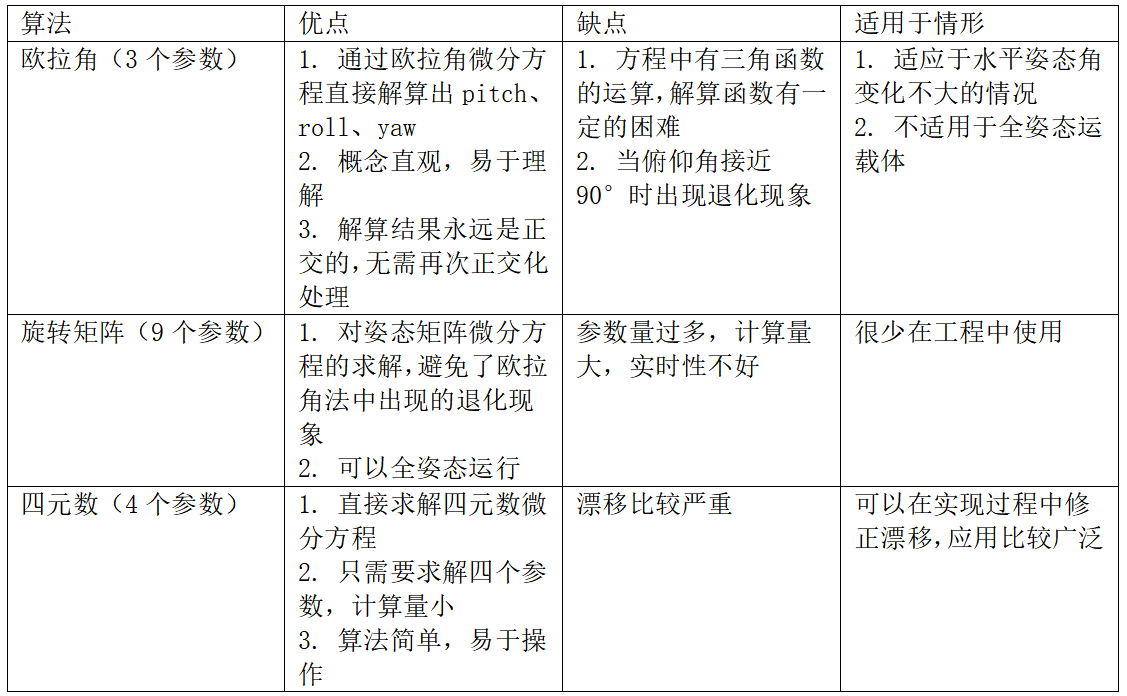三種表示算法的比較 （1）歐拉角、四元數、旋轉矩陣算法比較  在多旋翼的源碼中更多使用的是旋轉矩陣和四元數，因為歐拉角存在奇點問題，難用于計算，更多是給人一種直觀的表現,，而且歐拉角還存在**旋轉萬向鎖問題**，會導致自由度的缺失，達不到預期效果。而旋轉矩陣更多用于兩個坐標系之間的轉換，姿態表示更多使用的是四元數。 * [旋轉萬向鎖問題視頻講解](https://haokan.baidu.com/v?vid=4922356392425204532&pd=bjh&fr=bjhauthor&type=video) * [旋轉萬向鎖問題圖文講解，轉載>>http://blog.csdn.net/andrewfan](https://www.cnblogs.com/driftingclouds/p/6540222.html) # 6. 三種表示算法的轉換（重點）     歐拉角、旋轉矩陣、四元數之間可以相互轉換：  # 7. 重規范化     重規范化用來解決使用旋轉矩陣，或四元數解算姿態過程中產生的以下兩個誤差： **1.積分誤差：** 數值積分采用有限時間步長和具有有限采樣率的數據。根據所使 用的數值積分方法，對采樣的數據做特定的假設。我們所使用的方法假設在每 個時間步長內旋轉速度恒定不變。這將引入正比于旋轉加速度的誤差。 **2.量化誤差：** 無論使用哪種方法表示量值，這些表達都是有限的，所以會存在量化誤差。從模數轉換開始，到執行任何無法保留計算結果所有位數的計算，量化誤差都將不斷累積。如計算機無法保證其精度而產生的誤差。     重規范化思路包括兩個過程：歸一化和單位化。步驟如下： **（1）歸一化**     兩個向量的誤差可以使用點乘來計算，如下： :-: `$ \overrightarrow{X} =\begin{bmatrix} \overrightarrow{{r_{xx}}}\\ \overrightarrow{r_{xy}}\\ \overrightarrow{r_{xz}}\\ \end{bmatrix} $`，`$ \overrightarrow{Y} =\begin{bmatrix} \overrightarrow{{r_{yx}}}\\ \overrightarrow{r_{yy}}\\ \overrightarrow{r_{yz}}\\ \end{bmatrix} $` ```[tex] error=\overrightarrow{X} \cdot \overrightarrow{Y} =\overrightarrow{X}^{T} \cdot \overrightarrow{Y} = \begin{bmatrix} \overrightarrow{r_{xx}} & \overrightarrow{r_{xy}} & \overrightarrow{r_{xz}} \end{bmatrix}\begin{bmatrix} \overrightarrow{r_{yx}} \\ \overrightarrow{r_{yy}} \\ \overrightarrow{r_{yz}} \end{bmatrix}.................................................(4-7) ``` 把誤差均分給 X軸 與 Y軸，并近似地將 X軸 與 Y軸分別向相反的方向轉動，在此將 X軸 與 Y軸 互相修正，具體操作如下： ```[tex] \left\{\begin{matrix} \begin{bmatrix} \overrightarrow{r_{xx}} \\ \overrightarrow{r_{xy}} \\ \overrightarrow{r_{xz}} \end{bmatrix}_{orthogonal} = \overrightarrow{X}_{orthogonal} = \overrightarrow{X} - \frac{error}{2} \overrightarrow{Y}\\ \begin{bmatrix} \overrightarrow{r_{yx}} \\ \overrightarrow{r_{yy}} \\ \overrightarrow{r_{yz}} \end{bmatrix}_{orthogonal} = \overrightarrow{Y}_{orthogonal} = \overrightarrow{Y} - \frac{error}{2} \overrightarrow{X} \end{matrix}\right. .................................................(4-8) ``` 下一步調整方向余弦的 Z 軸，使得 Z軸 與 X軸 和 Y軸 均正交。這里采用的方法是簡單地重新計算 Z軸，使其等于 X軸 與 Y軸的外積。如下： ```[tex] \begin{bmatrix} \overrightarrow{r_{zx}} \\ \overrightarrow{r_{zy}} \\ \overrightarrow{r_{zz}} \end{bmatrix}_{orthogonal} = \overrightarrow{Z}_{orthogonal} = \overrightarrow{X}_{orthogonal} × \overrightarrow{Y}_{orthogonal}.................................................(4-9) ``` **（2）單位化**     單位化是調整方向余弦矩陣每一行的大小使其等于 1。一種方法是：每行的每個元素÷該行元素平方和的二次根。然而有一種更簡單的方法，鑒于每行的大小與1相差不大，所以可以采用泰勒展開進行單位化。如下： ```[tex] \left\{\begin{matrix} \overrightarrow{X}_{orthogonal} = \frac{1}{2}(3-\overrightarrow{X}_{orthogonal} \cdot \overrightarrow{X}_{orthogonal} ) \overrightarrow{X}_{orthogonal} \\ \overrightarrow{Y}_{orthogonal} = \frac{1}{2}(3-\overrightarrow{Y}_{orthogonal} \cdot \overrightarrow{Y}_{orthogonal} ) \overrightarrow{Y}_{orthogonal} \\ \overrightarrow{Z}_{orthogonal} = \frac{1}{2}(3-\overrightarrow{Z}_{orthogonal} \cdot \overrightarrow{Z}_{orthogonal} ) \overrightarrow{Z}_{orthogonal} \end{matrix}\right..................................................(4-10) ```     采用該方法單位化的好處是：既沒有采用更多的乘法和加法，同時也完全移除了除法與平方根的運算。在每一步積分都執行上述重規范化操作，執行周期為0.02s。如果在代碼中發現以**normal**至此重規范化操作完畢。