四元數的姿態解算就是求解四元數的微分方程:

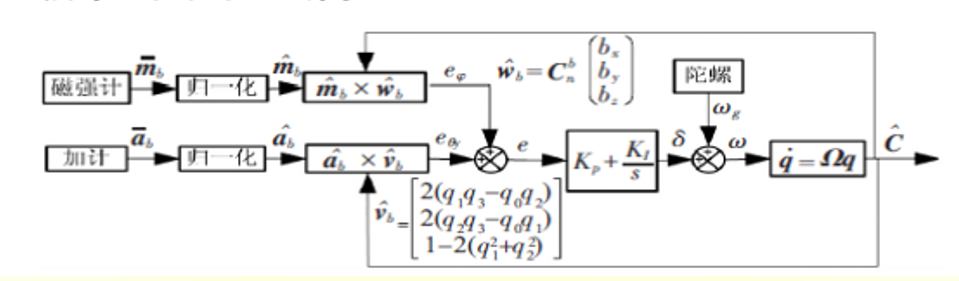
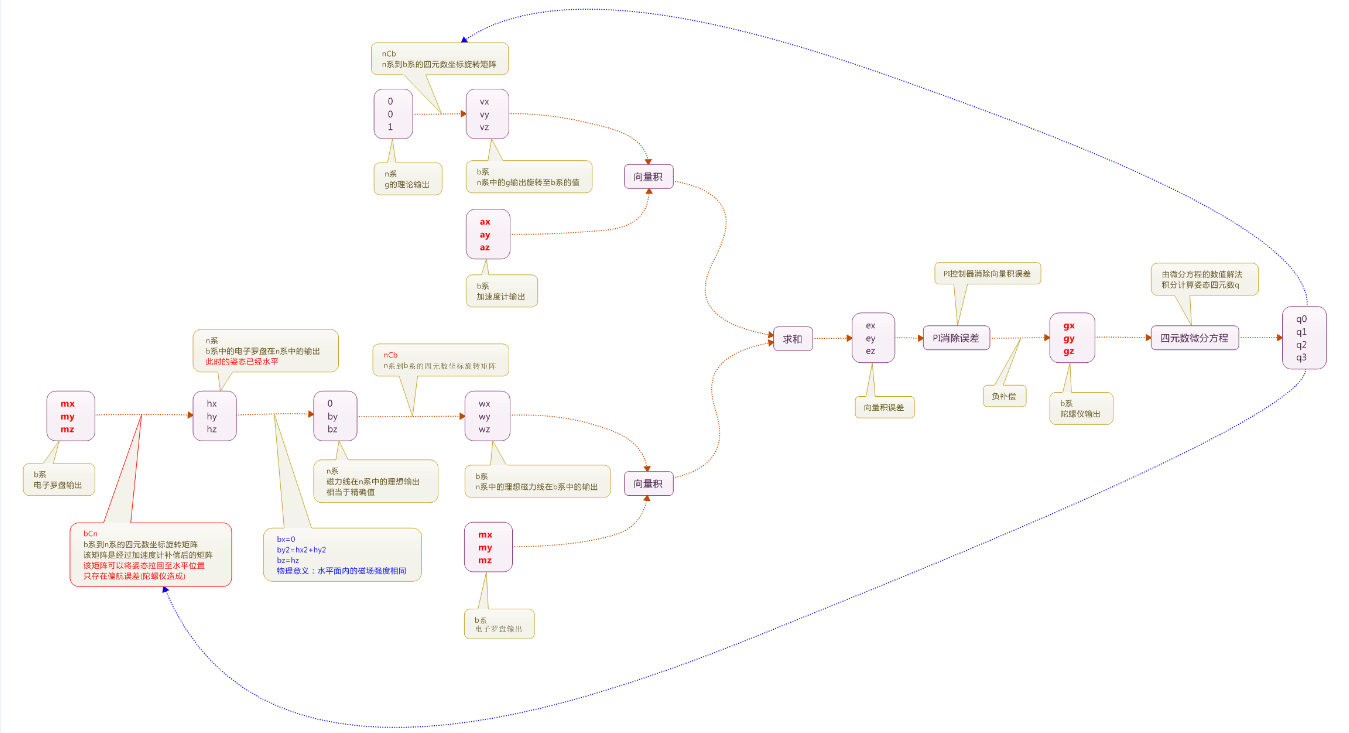
:-: 圖 4.2.2-1 四元素姿態解算流程
下面為四元數進行姿態解算的具體步驟:
**1. 初始化四元數**
姿態計算開始,將已知載體的初始姿態角帶入式4.2.2-1,求出初始時刻的四元數:
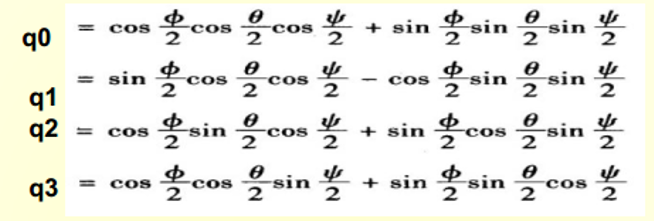-------------(4.2.2-1)
**2. 獲取角速度、加速度、磁力計的值**
陀螺儀測量得到的角速度為:`$ [w_x, w_y, w_z] $`,加速度計測量得到的加速度為:`$ [a_x, a_y, a_z] $`,磁力計測量得到的磁場為:`$ [m_x, m_y, m_z] $`。
**3. 將加速度計測量值、磁力計測量值化為單位向量**
**4. 從四元數中獲取重力向量和磁場向量**
**(1)通過旋轉矩陣乘以加速度計的輸出值得到重力向量`$ [\nu_x, \nu_y, \nu_z] $`**

加速度計的實際測量值為`$ [a_x, a_y, a_z] $`,它與重力向量`$ [\nu_x, \nu_y, \nu_z] $`同是表示在 b坐標系下的向量,它們之間的誤差按式(4.2.2-3)計算:
```[tex]
[e_x, e_y, e_z] = [\nu_x, \nu_y, \nu_z] × [a_x, a_y, a_z]-------------(4.2.2-3)
```
存在誤差的原因是:通過對陀螺儀測得的角速度進行積分獲取姿態角時存在的積分誤差,從而導致重力向量`$ [\nu_x, \nu_y, \nu_z] $`的不準確。
**(2)通過旋轉矩陣乘以磁力計的輸出值得到磁場向量**
磁力線由北指向南,近乎垂直于地球表面。由于Y軸與磁力線垂直,所以在Y軸上的磁場為 0 ,地球磁場就為:`$ [b_x, 0, b_z] $`,但是這個磁場向量有時是未知的,所以需要經過以下兩個步驟才能得到準確角速度值。
1)求出磁場向量
-----------------------------(4.2.2-X)
2)求出角速度
磁力計在XOY平面上(n系)的向量大小必定相同,令`$ b_x = \sqrt{h_{x}^{2} + h_{x}^{2}},b_z = h_z,b_y = 0 $`,然后通過式(4.2.2-X1)求出角速度:
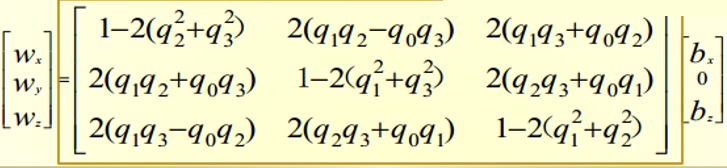-----------------------------(4.2.2-X1)
誤差為:
```[tex]
[e_x, e_y, e_z] = [m_x, m_y, m_z] × [w_x, w_y, w_z]-------------(4.2.2-3a)
```
**5. 計算誤差**
-----------------------------(4.2.2-X)
**6. 利用誤差修正陀螺儀**
使用PI算法來修改誤差:
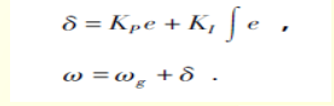-----------------------------(4.2.2-4)
`$ K_{p} $`比例系數,`$ e $`誤差,`$ K_{i} $`積分系數,`$ w $`為修正后的陀螺儀數據(角速度)。
**7. 利用修正后的陀螺儀數值更新四元數**
利用一階龍格—庫塔法求解微分方程,一階龍格—庫塔法表達式如式(4.2.2-5)
```[tex]
\dot{x} = f[x(t), w(t)]x(t+T) = x(t) + Tf[x(t), w(t)]---------(4.2.2-5)
```
四元數更新如式(4.2.2-6):
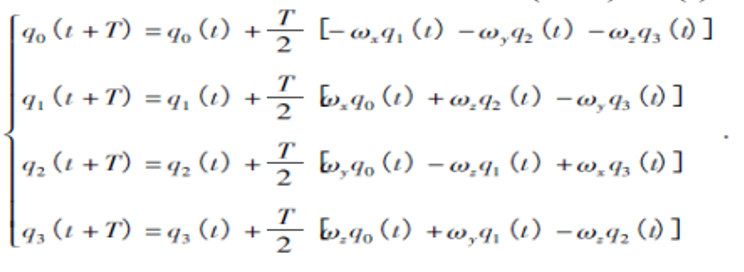------------(4.2.2-6)
第**4**步到第**7**步需要不斷地迭代,直到滿足為止。
**8. 將更新后的四元素規范化**
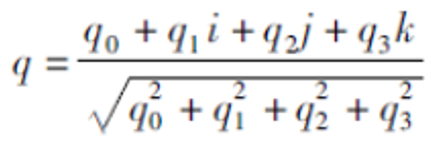---------(4.2.2-7)
**9. 將四元數轉換為歐拉角**
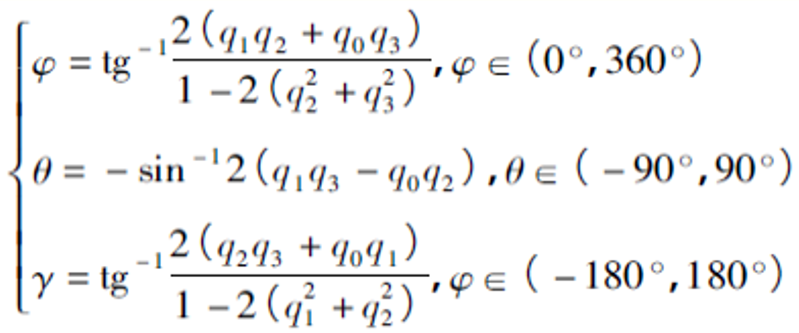---------(4.2.2-8)
至此,四元數的姿態解算就完成了。下圖表示四元素姿態的解算流程。