## 最長回文子串 ### 題目描述 給定一個字符串，求它的最長回文子串的長度。 ### 分析與解法 最容易想到的辦法是枚舉所有的子串，分別判斷其是否為回文。這個思路初看起來是正確的，但卻做了很多無用功，如果一個長的子串包含另一個短一些的子串，那么對子串的回文判斷其實是不需要的。 #### 解法一 那么如何高效的進行判斷呢？我們想想，如果一段字符串是回文，那么以某個字符為中心的前綴和后綴都是相同的，例如以一段回文串“aba”為例，以b為中心，它的前綴和后綴都是相同的，都是a。 那么，我們是否可以可以枚舉中心位置，然后再在該位置上用擴展法，記錄并更新得到的最長的回文長度呢？答案是肯定的，參考代碼如下： ```cpp int LongestPalindrome(const char *s, int n) { int i, j, max,c; if (s == 0 || n < 1) return 0; max = 0; for (i = 0; i < n; ++i) { // i is the middle point of the palindrome for (j = 0; (i - j >= 0) && (i + j < n); ++j){ // if the length of the palindrome is odd if (s[i - j] != s[i + j]) break; c = j * 2 + 1; } if (c > max) max = c; for (j = 0; (i - j >= 0) && (i + j + 1 < n); ++j){ // for the even case if (s[i - j] != s[i + j + 1]) break; c = j * 2 + 2; } if (c > max) max = c; } return max; } ``` 代碼稍微難懂一點的地方就是內層的兩個 for 循環，它們分別對于以 i 為中心的，長度為奇數和偶數的兩種情況，整個代碼遍歷中心位置 i 并以之擴展，找出最長的回文。 #### 解法二、O(N)解法 在上文的解法一：枚舉中心位置中，我們需要特別考慮字符串的長度是奇數還是偶數，所以導致我們在編寫代碼實現的時候要把奇數和偶數的情況分開編寫，是否有一種方法，可以不用管長度是奇數還是偶數，而統一處理呢？比如是否能把所有的情況全部轉換為奇數處理？ 答案還是肯定的。這就是下面我們將要看到的Manacher算法，且這個算法求最長回文子串的時間復雜度是線性O(N)的。 首先通過在每個字符的兩邊都插入一個特殊的符號，將所有可能的奇數或偶數長度的回文子串都轉換成了奇數長度。比如 abba 變成 #a#b#b#a#， aba變成 #a#b#a#。 此外，為了進一步減少編碼的復雜度，可以在字符串的開始加入另一個特殊字符，這樣就不用特殊處理越界問題，比如$#a#b#a#。 以字符串12212321為例，插入#和$這兩個特殊符號，變成了 S[] = "$#1#2#2#1#2#3#2#1#"，然后用一個數組 P[i] 來記錄以字符S[i]為中心的最長回文子串向左或向右擴張的長度（包括S[i]）。 比如S和P的對應關系： - S # 1 # 2 # 2 # 1 # 2 # 3 # 2 # 1 # - P 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1 可以看出，P[i]-1正好是原字符串中最長回文串的總長度，為5。 接下來怎么計算P[i]呢？Manacher算法增加兩個輔助變量id和mx，其中id表示最大回文子串中心的位置，mx則為id+P[id]，也就是最大回文子串的邊界。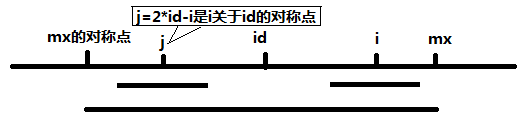得到一個很重要的結論： - 如果mx > i，那么P[i] >= Min(P[2 * id - i], mx - i) C代碼如下： ```c //mx > i，那么P[i] >= MIN(P[2 * id - i], mx - i) //故誰小取誰 if (mx - i > P[2*id - i]) P[i] = P[2*id - i]; else //mx-i <= P[2*id - i] P[i] = mx - i; ``` 下面，令j = 2*id - i，也就是說j是i關于id的對稱點。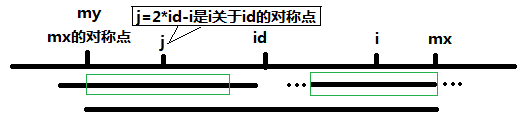 當 mx - i > P[j] 的時候，以S[j]為中心的回文子串包含在以S[id]為中心的回文子串中，由于i和j對稱，以S[i]為中心的回文子串必然包含在以S[id]為中心的回文子串中，所以必有P[i] = P[j]；  當 P[j] >= mx - i 的時候，以S[j]為中心的回文子串不一定完全包含于以S[id]為中心的回文子串中，但是基于對稱性可知，下圖中兩個綠框所包圍的部分是相同的，也就是說以S[i]為中心的回文子串，其向右至少會擴張到mx的位置，也就是說 P[i] >= mx - i。至于mx之后的部分是否對稱，再具體匹配。  此外，對于 mx <= i 的情況，因為無法對 P[i]做更多的假設，只能讓P[i] = 1，然后再去匹配。 綜上，關鍵代碼如下： ```c //輸入，并處理得到字符串s int p[1000], mx = 0, id = 0; memset(p, 0, sizeof(p)); for (i = 1; s[i] != '\0'; i++) { p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1; while (s[i + p[i]] == s[i - p[i]]) p[i]++; if (i + p[i] > mx) { mx = i + p[i]; id = i; } } //找出p[i]中最大的 ``` 此Manacher算法使用id、mx做配合，可以在每次循環中，直接對P[i]的快速賦值，從而在計算以i為中心的回文子串的過程中，不必每次都從1開始比較，減少了比較次數，最終使得求解最長回文子串的長度達到線性O(N)的時間復雜度。 參考：http://www.felix021.com/blog/read.php?2040 。另外，這篇文章也不錯：http://leetcode.com/2011/11/longest-palindromic-substring-part-ii.html 。