# 矩陣相乘
## 題目描述
請編程實現矩陣乘法,并考慮當矩陣規模較大時的優化方法。
## 分析與解法
根據wikipedia上的介紹:兩個矩陣的乘法僅當第一個矩陣A的行數和另一個矩陣B的列數相等時才能定義。如A是m×n矩陣,B是n×p矩陣,它們的乘積AB是一個m×p矩陣,它的一個元素其中 1 ≤ i ≤ m, 1 ≤ j ≤ p。

值得一提的是,矩陣乘法滿足結合律和分配率,但并不滿足交換律,如下圖所示的這個例子,兩個矩陣交換相乘后,結果變了:

下面咱們來具體解決這個矩陣相乘的問題。
### 解法一、暴力解法
其實,通過前面的分析,我們已經很明顯的看出,兩個具有相同維數的矩陣相乘,其復雜度為O(n^3),參考代碼如下:
```cpp
//矩陣乘法,3個for循環搞定
void MulMatrix(int** matrixA, int** matrixB, int** matrixC)
{
for(int i = 0; i < 2; ++i)
{
for(int j = 0; j < 2; ++j)
{
matrixC[i][j] = 0;
for(int k = 0; k < 2; ++k)
{
matrixC[i][j] += matrixA[i][k] * matrixB[k][j];
}
}
}
}
```
### 解法二、Strassen算法
在解法一中,我們用了3個for循環搞定矩陣乘法,但當兩個矩陣的維度變得很大時,O(n^3)的時間復雜度將會變得很大,于是,我們需要找到一種更優的解法。
一般說來,當數據量一大時,我們往往會把大的數據分割成小的數據,各個分別處理。遵此思路,如果丟給我們一個很大的兩個矩陣呢,是否可以考慮分治的方法循序漸進處理各個小矩陣的相乘,因為我們知道一個矩陣是可以分成更多小的矩陣的。
如下圖,當給定一個兩個二維矩陣A B時:

這兩個矩陣A B相乘時,我們發現在相乘的過程中,有8次乘法運算,4次加法運算:

矩陣乘法的復雜度主要就是體現在相乘上,而多一兩次的加法并不會讓復雜度上升太多。故此,我們思考,是否可以讓矩陣乘法的運算過程中乘法的運算次數減少,從而達到降低矩陣乘法的復雜度呢?答案是肯定的。
1969年,德國的一位數學家Strassen證明O(N^3)的解法并不是矩陣乘法的最優算法,他做了一系列工作使得最終的時間復雜度降低到了O(n^2.80)。
他是怎么做到的呢?還是用上文A B兩個矩陣相乘的例子,他定義了7個變量:

如此,Strassen算法的流程如下:
* 兩個矩陣A B相乘時,將A, B, C分成相等大小的方塊矩陣:

* 可以看出C是這么得來的:

* 現在定義7個新矩陣(*讀者可以思考下,這7個新矩陣是如何想到的*):

* 而最后的結果矩陣C 可以通過組合上述7個新矩陣得到:

表面上看,Strassen算法僅僅比通用矩陣相乘算法好一點,因為通用矩陣相乘算法時間復雜度是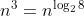,而Strassen算法復雜度只是
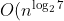=O(n^{2.807})})。但隨著n的變大,比如當n >> 100時,Strassen算法是比通用矩陣相乘算法變得更有效率。
如下圖所示:

根據wikipedia上的介紹,后來,Coppersmith–Winograd 算法把 N* N大小的矩陣乘法的時間復雜度降低到了: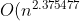}),而2010年,Andrew Stothers再度把復雜度降低到了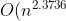}),一年后的2011年,Virginia Williams把復雜度最終定格為: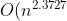})。
- 程序員如何準備面試中的算法
- 第一部分 數據結構
- 第一章 字符串
- 1.0 本章導讀
- 1.1 旋轉字符串
- 1.2 字符串包含
- 1.3 字符串轉換成整數
- 1.4 回文判斷
- 1.5 最長回文子串
- 1.6 字符串的全排列
- 1.10 本章習題
- 第二章 數組
- 2.0 本章導讀
- 2.1 尋找最小的 k 個數
- 2.2 尋找和為定值的兩個數
- 2.3 尋找和為定值的多個數
- 2.4 最大連續子數組和
- 2.5 跳臺階
- 2.6 奇偶排序
- 2.7 荷蘭國旗
- 2.8 矩陣相乘
- 2.9 完美洗牌
- 2.15 本章習題
- 第三章 樹
- 3.0 本章導讀
- 3.1 紅黑樹
- 3.2 B樹
- 3.3 最近公共祖先LCA
- 3.10 本章習題
- 第二部分 算法心得
- 第四章 查找匹配
- 4.1 有序數組的查找
- 4.2 行列遞增矩陣的查找
- 4.3 出現次數超過一半的數字
- 第五章 動態規劃
- 5.0 本章導讀
- 5.1 最大連續乘積子串
- 5.2 字符串編輯距離
- 5.3 格子取數
- 5.4 交替字符串
- 5.10 本章習題
- 第三部分 綜合演練
- 第六章 海量數據處理
- 6.0 本章導讀
- 6.1 關聯式容器
- 6.2 分而治之
- 6.3 simhash算法
- 6.4 外排序
- 6.5 MapReduce
- 6.6 多層劃分
- 6.7 Bitmap
- 6.8 Bloom filter
- 6.9 Trie樹
- 6.10 數據庫
- 6.11 倒排索引
- 6.15 本章習題
- 第七章 機器學習
- 7.1 K 近鄰算法
- 7.2 支持向量機
- 附錄 更多題型
- 附錄A 語言基礎
- 附錄B 概率統計
- 附錄C 智力邏輯
- 附錄D 系統設計
- 附錄E 操作系統
- 附錄F 網絡協議
- sift算法
- sift算法的編譯與實現
- 教你一步一步用c語言實現sift算法、上
- 教你一步一步用c語言實現sift算法、下
- 其它
- 40億個數中快速查找
- hash表算法
- 一致性哈希算法
- 倒排索引關鍵詞不重復Hash編碼
- 傅里葉變換算法、上
- 傅里葉變換算法、下
- 后綴樹
- 基于給定的文檔生成倒排索引的編碼與實踐
- 搜索關鍵詞智能提示suggestion
- 最小操作數
- 最短摘要的生成
- 最長公共子序列
- 木塊砌墻原稿
- 附近地點搜索
- 隨機取出其中之一元素
