6-安卓自定義View進階-貝塞爾曲線 · 我的Android Wiki

# Path之貝塞爾曲線 ### 作者微博: [@GcsSloop](http://weibo.com/GcsSloop) ### [【本系列相關文章】](https://github.com/GcsSloop/AndroidNote/tree/master/CustomView/README.md) 在上一篇文章[Path之基本圖形](https://github.com/GcsSloop/AndroidNote/blob/master/CustomView/Advance/%5B05%5DPath_Basic.md)中我們了解了Path的基本使用方法，本次了解Path中非常非常非常重要的內容-貝塞爾曲線。 ****** ## 一.Path常用方法表 > 為了兼容性(_偷懶_) 本表格中去除了在API21(即安卓版本5.0)以上才添加的方法。忍不住吐槽一下，為啥看起來有些順手就能寫的重載方法要等到API21才添加上啊。寶寶此刻內心也是崩潰的。 | 作用 | 相關方法 | 備注 | | ----------- | ---------------------------------------- | ---------------------------------------- | | 移動起點 | moveTo | 移動下一次操作的起點位置 | | 設置終點 | setLastPoint | 重置當前path中最后一個點位置，如果在繪制之前調用，效果和moveTo相同 | | 連接直線 | lineTo | 添加上一個點到當前點之間的直線到Path | | 閉合路徑 | close | 連接第一個點連接到最后一個點，形成一個閉合區域 | | 添加內容 | addRect, addRoundRect, addOval, addCircle, addPath, addArc, arcTo | 添加(矩形，圓角矩形，橢圓，圓，路徑，圓弧) 到當前Path (注意addArc和arcTo的區別) | | 是否為空 | isEmpty | 判斷Path是否為空 | | 是否為矩形 | isRect | 判斷path是否是一個矩形 | | 替換路徑 | set | 用新的路徑替換到當前路徑所有內容 | | 偏移路徑 | offset | 對當前路徑之前的操作進行偏移(不會影響之后的操作) | | 貝塞爾曲線 | quadTo, cubicTo | 分別為二次和三次貝塞爾曲線的方法 | | rXxx方法 | rMoveTo, rLineTo, rQuadTo, rCubicTo | **不帶r的方法是基于原點的坐標系(偏移量)， rXxx方法是基于當前點坐標系(偏移量)** | | 填充模式 | setFillType, getFillType, isInverseFillType, toggleInverseFillType | 設置,獲取,判斷和切換填充模式 | | 提示方法 | incReserve | 提示Path還有多少個點等待加入**(這個方法貌似會讓Path優化存儲結構)** | | 布爾操作(API19) | op | 對兩個Path進行布爾運算(即取交集、并集等操作) | | 計算邊界 | computeBounds | 計算Path的邊界 | | 重置路徑 | reset, rewind | 清除Path中的內容 **reset不保留內部數據結構，但會保留FillType.** **rewind會保留內部的數據結構，但不保留FillType** | | 矩陣操作 | transform | 矩陣變換 | ## 二.Path詳解上一次除了一些常用函數之外，講解的基本上都是直線，本次需要了解其中的曲線部分,說到曲線，就不得不提大名鼎鼎的貝塞爾曲線。它的發明者是下面這個人(法國數學家PierreBézier)。 ![](http://ww4.sinaimg.cn/large/005Xtdi2jw1f1ky5bw28pg305k07h3yo.gif) ### 貝塞爾曲線能干什么？貝塞爾曲線的運用是十分廣泛的，可以說**貝塞爾曲線奠定了計算機繪圖的基礎(_因為它可以將任何復雜的圖形用精確的數學語言進行描述_)**，在你不經意間就已經使用過它了。你會使用Photoshop的話，你可能會注意到里面有一個**鋼筆工具**，這個鋼筆工具核心就是貝塞爾曲線。你說你不會PS？沒關系，你如果看過前面的文章或者用過2D繪圖，肯定繪制過圓，圓弧，圓角矩形等這些東西。這里面的圓弧部分全部都是貝塞爾曲線的運用。 #### 貝塞爾曲線作用十分廣泛，簡單舉幾個的栗子: > * QQ小紅點拖拽效果 * 一些炫酷的下拉刷新控件 * 閱讀軟件的翻書效果 * 一些平滑的折線圖的制作 * 很多炫酷的動畫效果 ### 如何輕松入門貝塞爾曲線？雖然貝塞爾曲線用途非常廣泛，然而目前貌似并沒有適合的中文教程，能夠搜索出來Android關于貝塞爾曲線的中文文章基本可以分為以下幾種： * 科普型(只是讓人了解貝塞爾，并沒有實質性的內容) * 裝逼型(擺出來一大堆公式，引用一堆英文原文) * 基礎型(僅僅是講解貝塞爾曲線的兩個函數用法) * 實戰型(根據實例講解其中貝塞爾曲線的運用) 以上幾種類型中比較有用的就是基礎型和實戰型，但兩者各有不足，本文會綜合兩者內容，從零開始學習貝塞爾曲線。 ### 第一步.理解貝塞爾曲線的原理此處理解貝塞爾曲線并非是學會公式的推導過程(不是推倒(?*?ω?)?)，而是要了解貝塞爾曲線是如何生成的。貝塞爾曲線是用一系列點來控制曲線狀態的，我將這些點簡單分為兩類： | 類型 | 作用 | | ---- | ------------ | | 數據點 | 確定曲線的起始和結束位置 | | 控制點 | 確定曲線的彎曲程度 | > 此處暫時僅作了解概念，接下來就會講解其中詳細的含義。 **一階曲線原理：** 一階曲線是沒有控制點的，僅有兩個數據點(A 和 B)，最終效果一個線段。 ![](http://ww1.sinaimg.cn/large/005Xtdi2jw1f35of045w8j308c0dwq2z.jpg) > **上圖表示的是一階曲線生成過程中的某一個階段，動態過程可以參照下圖(本文中貝塞爾曲線相關的動態演示圖片來自維基百科)。** ![](https://upload.wikimedia.org/wikipedia/commons/0/00/B%C3%A9zier_1_big.gif) > **PS：一階曲線其實就是前面講解過的lineTo。** **二階曲線原理：** 二階曲線由兩個數據點(A 和 C)，一個控制點(B)來描述曲線狀態，大致如下： ![](http://ww3.sinaimg.cn/large/005Xtdi2jw1f35p4913k7j308c0dw74d.jpg) 上圖中紅色曲線部分就是傳說中的二階貝塞爾曲線，那么這條紅色曲線是如何生成的呢？接下來我們就以其中的一個狀態分析一下： ![](http://ww4.sinaimg.cn/large/005Xtdi2jw1f361bjqj2vj308c0dwwem.jpg) 連接AB BC，并在AB上取點D，BC上取點E，使其滿足條件： <img src="http://chart.googleapis.com/chart?cht=tx&chl=%5Cfrac%7BAD%7D%7BAB%7D%20%3D%20%5Cfrac%7BBE%7D%7BBC%7D" style="border:none;" /> ![](http://ww2.sinaimg.cn/large/005Xtdi2jw1f361oje6h1j308c0dwdg0.jpg) 連接DE，取點F，使得: <img src="http://chart.googleapis.com/chart?cht=tx&chl=%5Cfrac%7BAD%7D%7BAB%7D%20%3D%20%5Cfrac%7BBE%7D%7BBC%7D%20%3D%20%5Cfrac%7BDF%7D%7BDE%7D" style="border:none;" /> 這樣獲取到的點F就是貝塞爾曲線上的一個點，動態過程如下： ![](https://upload.wikimedia.org/wikipedia/commons/3/3d/B%C3%A9zier_2_big.gif) > **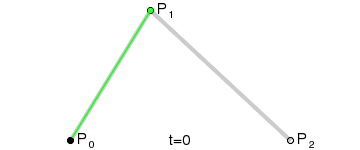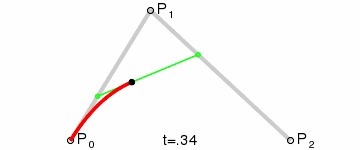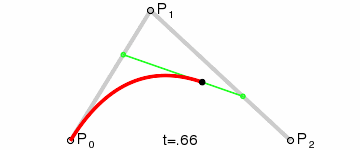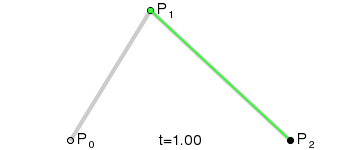PS: 二階曲線對應的方法是quadTo** **三階曲線原理：** 三階曲線由兩個數據點(A 和 D)，兩個控制點(B 和 C)來描述曲線狀態，如下： ![](http://ww2.sinaimg.cn/large/005Xtdi2gw1f36myeqcu5j308c0dwdg2.jpg) 三階曲線計算過程與二階類似，具體可以見下圖動態效果： ![](https://upload.wikimedia.org/wikipedia/commons/d/db/B%C3%A9zier_3_big.gif) > **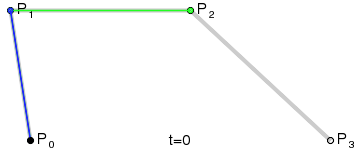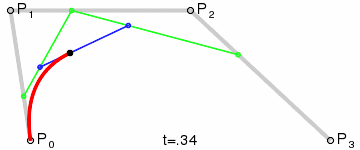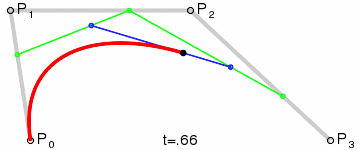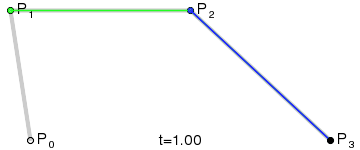PS: 三階曲線對應的方法是cubicTo** #### [貝塞爾曲線速查表](https://github.com/GcsSloop/AndroidNote/blob/master/QuickChart/Bezier.md) #### 強烈推薦[點擊這里](http://bezier.method.ac/)練習貝塞爾曲線，可以加深對貝塞爾曲線的理解程度。 ### 第二步.了解貝塞爾曲線相關函數使用方法 #### 一階曲線：一階曲線是一條線段，非常簡單，可以參見上一篇文章[Path之基本操作](https://github.com/GcsSloop/AndroidNote/blob/master/CustomView/Advance/5%5DPath_Basic.md)，此處就不詳細講解了。 #### 二階曲線：通過上面對二階曲線的簡單了解，我們知道二階曲線是由兩個數據點，一個控制點構成，接下來我們就用一個實例來演示二階曲線是如何運用的。首先，兩個數據點是控制貝塞爾曲線開始和結束的位置，比較容易理解，而控制點則是控制貝塞爾的彎曲狀態，相對來說比較難以理解，所以本示例重點在于理解貝塞爾曲線彎曲狀態與控制點的關系，廢話不多說，先上效果圖： ![](http://ww2.sinaimg.cn/large/005Xtdi2gw1f39vugjg0vg308c0e8409.gif) > 為了更加容易看出控制點與曲線彎曲程度的關系，上圖中繪制出了輔助點和輔助線，從上面的動態圖可以看出，貝塞爾曲線在動態變化過程中有類似于橡皮筋一樣的彈性效果，因此在制作一些彈性效果的時候很常用。主要代碼如下： ``` java public class Bezier extends View { private Paint mPaint; private int centerX, centerY; private PointF start, end, control; public Bessel1(Context context) { super(context); mPaint = new Paint(); mPaint.setColor(Color.BLACK); mPaint.setStrokeWidth(8); mPaint.setStyle(Paint.Style.STROKE); mPaint.setTextSize(60); start = new PointF(0,0); end = new PointF(0,0); control = new PointF(0,0); } @Override protected void onSizeChanged(int w, int h, int oldw, int oldh) { super.onSizeChanged(w, h, oldw, oldh); centerX = w/2; centerY = h/2; // 初始化數據點和控制點的位置 start.x = centerX-200; start.y = centerY; end.x = centerX+200; end.y = centerY; control.x = centerX; control.y = centerY-100; } @Override public boolean onTouchEvent(MotionEvent event) { // 根據觸摸位置更新控制點，并提示重繪 control.x = event.getX(); control.y = event.getY(); invalidate(); return true; } @Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); // 繪制數據點和控制點 mPaint.setColor(Color.GRAY); mPaint.setStrokeWidth(20); canvas.drawPoint(start.x,start.y,mPaint); canvas.drawPoint(end.x,end.y,mPaint); canvas.drawPoint(control.x,control.y,mPaint); // 繪制輔助線 mPaint.setStrokeWidth(4); canvas.drawLine(start.x,start.y,control.x,control.y,mPaint); canvas.drawLine(end.x,end.y,control.x,control.y,mPaint); // 繪制貝塞爾曲線 mPaint.setColor(Color.RED); mPaint.setStrokeWidth(8); Path path = new Path(); path.moveTo(start.x,start.y); path.quadTo(control.x,control.y,end.x,end.y); canvas.drawPath(path, mPaint); } } ``` #### 三階曲線：三階曲線由兩個數據點和兩個控制點來控制曲線狀態。 ![](http://ww1.sinaimg.cn/large/005Xtdi2gw1f3bmilt4flg308c0e8q5e.gif) 代碼: ``` java public class Bezier2 extends View { private Paint mPaint; private int centerX, centerY; private PointF start, end, control1, control2; private boolean mode = true; public Bezier2(Context context) { this(context, null); } public Bezier2(Context context, AttributeSet attrs) { super(context, attrs); mPaint = new Paint(); mPaint.setColor(Color.BLACK); mPaint.setStrokeWidth(8); mPaint.setStyle(Paint.Style.STROKE); mPaint.setTextSize(60); start = new PointF(0, 0); end = new PointF(0, 0); control1 = new PointF(0, 0); control2 = new PointF(0, 0); } public void setMode(boolean mode) { this.mode = mode; } @Override protected void onSizeChanged(int w, int h, int oldw, int oldh) { super.onSizeChanged(w, h, oldw, oldh); centerX = w / 2; centerY = h / 2; // 初始化數據點和控制點的位置 start.x = centerX - 200; start.y = centerY; end.x = centerX + 200; end.y = centerY; control1.x = centerX; control1.y = centerY - 100; control2.x = centerX; control2.y = centerY - 100; } @Override public boolean onTouchEvent(MotionEvent event) { // 根據觸摸位置更新控制點，并提示重繪 if (mode) { control1.x = event.getX(); control1.y = event.getY(); } else { control2.x = event.getX(); control2.y = event.getY(); } invalidate(); return true; } @Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); //drawCoordinateSystem(canvas); // 繪制數據點和控制點 mPaint.setColor(Color.GRAY); mPaint.setStrokeWidth(20); canvas.drawPoint(start.x, start.y, mPaint); canvas.drawPoint(end.x, end.y, mPaint); canvas.drawPoint(control1.x, control1.y, mPaint); canvas.drawPoint(control2.x, control2.y, mPaint); // 繪制輔助線 mPaint.setStrokeWidth(4); canvas.drawLine(start.x, start.y, control1.x, control1.y, mPaint); canvas.drawLine(control1.x, control1.y,control2.x, control2.y, mPaint); canvas.drawLine(control2.x, control2.y,end.x, end.y, mPaint); // 繪制貝塞爾曲線 mPaint.setColor(Color.RED); mPaint.setStrokeWidth(8); Path path = new Path(); path.moveTo(start.x, start.y); path.cubicTo(control1.x, control1.y, control2.x,control2.y, end.x, end.y); canvas.drawPath(path, mPaint); } } ``` > 三階曲線相比于二階曲線可以制作更加復雜的形狀，但是對于高階的曲線，用低階的曲線組合也可達到相同的效果，就是傳說中的**降階**。因此我們對貝塞爾曲線的封裝方法一般最高只到三階曲線。 #### 降階與升階 | 類型 | 釋義 | 變化 | | ---- | -------------------------------- | -------------------------- | | 降階 | 在保持曲線形狀與方向不變的情況下，減少控制點數量，即降低曲線階數 | 方法變得簡單，數據點變多，控制點可能減少，靈活性變弱 | | 升階 | 在保持曲線形狀與方向不變的情況下，增加控制點數量，即升高曲線階數 | 方法更加復雜，數據點不變，控制點增加，靈活性變強 | ### 第三步.貝塞爾曲線使用實例 **在制作這個實例之前，首先要明確一個內容，就是在什么情況下需要使用貝塞爾曲線？** > 需要繪制不規則圖形時？當然不是！目前來說，我覺得使用貝塞爾曲線主要有以下幾個方面(僅個人拙見，可能存在錯誤，歡迎指正) | 序號 | 內容 | 用例 | | ---- | ---------------------------- | -------------- | | 1 | 事先不知道曲線狀態，需要實時計算時 | 天氣預報氣溫變化的平滑折線圖 | | 2 | 顯示狀態會根據用戶操作改變時 | QQ小紅點，仿真翻書效果 | | 3 | 一些比較復雜的運動狀態(配合PathMeasure使用) | 復雜運動狀態的動畫效果 | 至于只需要一個靜態的曲線圖形的情況，用圖片豈不是更好，大量的計算會很不劃算。如果是顯示SVG矢量圖的話，已經有相關的解析工具了(內部依舊運用的有貝塞爾曲線)，不需要手動計算。 **貝塞爾曲線的主要優點是可以實時控制曲線狀態，并可以通過改變控制點的狀態實時讓曲線進行平滑的狀態變化。** ### 接下來我們就用一個簡單的示例讓一個圓漸變成為心形： #### 效果圖： ![](http://ww2.sinaimg.cn/large/005Xtdi2jw1f3cg2cs7lyg308c0e8gpn.gif) #### 思路分析：我們最終的需要的效果是將一個圓轉變成一個心形，通過分析可知，圓可以由四段三階貝塞爾曲線組合而成，如下： ![](http://ww3.sinaimg.cn/large/005Xtdi2gw1f3chnpgub3j308c0e7weq.jpg) 心形也可以由四段的三階的貝塞爾曲線組成，如下： ![](http://ww2.sinaimg.cn/large/005Xtdi2gw1f3chod09sbj308c0e774j.jpg) 兩者的差別僅僅在于數據點和控制點位置不同，因此只需要調整數據點和控制點的位置，就能將圓形變為心形。 #### 核心難點： ##### 1.如何得到數據點和控制點的位置？關于使用繪制圓形的數據點與控制點早就已經有人詳細的計算好了，可以參考stackoverflow的一個回答[How to create circle with Bézier curves?](http://stackoverflow.com/questions/1734745/how-to-create-circle-with-b%C3%A9zier-curves)其中的數據只需要拿來用即可。而對于心形的數據點和控制點，可以由圓形的部分數據點和控制點平移后得到，具體參數可以自己慢慢調整到一個滿意的效果。 ##### 2.如何達到漸變效果？漸變其實就是每次對數據點和控制點稍微移動一點，然后重繪界面，在短時間多次的調整數據點與控制點，使其逐漸接近目標值，通過不斷的重繪界面達到一種漸變的效果。過程可以參照下圖動態效果： ![](http://ww2.sinaimg.cn/large/005Xtdi2jw1f3ch74ewiig308c0e8wic.gif) #### 代碼： ``` java public class Bezier3 extends View { private static final float C = 0.551915024494f; // 一個常量，用來計算繪制圓形貝塞爾曲線控制點的位置 private Paint mPaint; private int mCenterX, mCenterY; private PointF mCenter = new PointF(0,0); private float mCircleRadius = 200; // 圓的半徑 private float mDifference = mCircleRadius*C; // 圓形的控制點與數據點的差值 private float[] mData = new float[8]; // 順時針記錄繪制圓形的四個數據點 private float[] mCtrl = new float[16]; // 順時針記錄繪制圓形的八個控制點 private float mDuration = 1000; // 變化總時長 private float mCurrent = 0; // 當前已進行時長 private float mCount = 100; // 將時長總共劃分多少份 private float mPiece = mDuration/mCount; // 每一份的時長 public Bezier3(Context context) { this(context, null); } public Bezier3(Context context, AttributeSet attrs) { super(context, attrs); mPaint = new Paint(); mPaint.setColor(Color.BLACK); mPaint.setStrokeWidth(8); mPaint.setStyle(Paint.Style.STROKE); mPaint.setTextSize(60); // 初始化數據點 mData[0] = 0; mData[1] = mCircleRadius; mData[2] = mCircleRadius; mData[3] = 0; mData[4] = 0; mData[5] = -mCircleRadius; mData[6] = -mCircleRadius; mData[7] = 0; // 初始化控制點 mCtrl[0] = mData[0]+mDifference; mCtrl[1] = mData[1]; mCtrl[2] = mData[2]; mCtrl[3] = mData[3]+mDifference; mCtrl[4] = mData[2]; mCtrl[5] = mData[3]-mDifference; mCtrl[6] = mData[4]+mDifference; mCtrl[7] = mData[5]; mCtrl[8] = mData[4]-mDifference; mCtrl[9] = mData[5]; mCtrl[10] = mData[6]; mCtrl[11] = mData[7]-mDifference; mCtrl[12] = mData[6]; mCtrl[13] = mData[7]+mDifference; mCtrl[14] = mData[0]-mDifference; mCtrl[15] = mData[1]; } @Override protected void onSizeChanged(int w, int h, int oldw, int oldh) { super.onSizeChanged(w, h, oldw, oldh); mCenterX = w / 2; mCenterY = h / 2; } @Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); drawCoordinateSystem(canvas); // 繪制坐標系 canvas.translate(mCenterX, mCenterY); // 將坐標系移動到畫布中央 canvas.scale(1,-1); // 翻轉Y軸 drawAuxiliaryLine(canvas); // 繪制貝塞爾曲線 mPaint.setColor(Color.RED); mPaint.setStrokeWidth(8); Path path = new Path(); path.moveTo(mData[0],mData[1]); path.cubicTo(mCtrl[0], mCtrl[1], mCtrl[2], mCtrl[3], mData[2], mData[3]); path.cubicTo(mCtrl[4], mCtrl[5], mCtrl[6], mCtrl[7], mData[4], mData[5]); path.cubicTo(mCtrl[8], mCtrl[9], mCtrl[10], mCtrl[11], mData[6], mData[7]); path.cubicTo(mCtrl[12], mCtrl[13], mCtrl[14], mCtrl[15], mData[0], mData[1]); canvas.drawPath(path, mPaint); mCurrent += mPiece; if (mCurrent < mDuration){ mData[1] -= 120/mCount; mCtrl[7] += 80/mCount; mCtrl[9] += 80/mCount; mCtrl[4] -= 20/mCount; mCtrl[10] += 20/mCount; postInvalidateDelayed((long) mPiece); } } // 繪制輔助線 private void drawAuxiliaryLine(Canvas canvas) { // 繪制數據點和控制點 mPaint.setColor(Color.GRAY); mPaint.setStrokeWidth(20); for (int i=0; i<8; i+=2){ canvas.drawPoint(mData[i],mData[i+1], mPaint); } for (int i=0; i<16; i+=2){ canvas.drawPoint(mCtrl[i], mCtrl[i+1], mPaint); } // 繪制輔助線 mPaint.setStrokeWidth(4); for (int i=2, j=2; i<8; i+=2, j+=4){ canvas.drawLine(mData[i],mData[i+1],mCtrl[j],mCtrl[j+1],mPaint); canvas.drawLine(mData[i],mData[i+1],mCtrl[j+2],mCtrl[j+3],mPaint); } canvas.drawLine(mData[0],mData[1],mCtrl[0],mCtrl[1],mPaint); canvas.drawLine(mData[0],mData[1],mCtrl[14],mCtrl[15],mPaint); } // 繪制坐標系 private void drawCoordinateSystem(Canvas canvas) { canvas.save(); // 繪制做坐標系 canvas.translate(mCenterX, mCenterY); // 將坐標系移動到畫布中央 canvas.scale(1,-1); // 翻轉Y軸 Paint fuzhuPaint = new Paint(); fuzhuPaint.setColor(Color.RED); fuzhuPaint.setStrokeWidth(5); fuzhuPaint.setStyle(Paint.Style.STROKE); canvas.drawLine(0, -2000, 0, 2000, fuzhuPaint); canvas.drawLine(-2000, 0, 2000, 0, fuzhuPaint); canvas.restore(); } } ``` ## 三.總結其實關于貝塞爾曲線最重要的是核心理解貝塞爾曲線的生成方式，只有理解了貝塞爾曲線的生成方式，才能更好的運用貝塞爾曲線。在上一篇末尾說本篇要涉及一點自相交圖形渲染問題，不幸的是，本篇沒有了，請期待下一篇(可能會在下一篇中出現o(*￣︶￣*)o)，下一篇依舊Path相關內容，教給大家一些更好玩的東西。解鎖新的境界之[【繪制一個彈性的圓】](http://www.jianshu.com/p/791d3a791ec2)： <img src="http://ww3.sinaimg.cn/large/005Xtdi2jw1f3cij475bhg30k00zk46m.gif" width=300 /> (,,? ? ?,,) #### PS: 由于本人水平有限，某些地方可能存在誤解或不準確，如果你對此有疑問可以提交Issues進行反饋。 ## About Me ### 作者微博: <a href="http://weibo.com/GcsSloop" target="_blank">@GcsSloop</a> <a href="https://github.com/GcsSloop/AndroidNote/blob/magic-world/FINDME.md" target="_blank"> <img src="http://ww4.sinaimg.cn/large/005Xtdi2gw1f1qn89ihu3j315o0dwwjc.jpg" width=300/> </a> ## 參考資料 [Path](http://developer.android.com/reference/android/graphics/Path.html) [Canvas](http://developer.android.com/reference/android/graphics/Canvas.html) [貝塞爾曲線掃盲](http://www.html-js.com/article/1628) [貝塞爾曲線-維基百科](https://zh.wikipedia.org/wiki/%E8%B2%9D%E8%8C%B2%E6%9B%B2%E7%B7%9A) [How to create circle with Bézier curves?](http://stackoverflow.com/questions/1734745/how-to-create-circle-with-b%C3%A9zier-curves) [三次貝塞爾曲線練習之彈性的圓](http://www.jianshu.com/p/791d3a791ec2)