[TOC] >[success] # 復雜度分析系方式 ~~~ 1.只關注循環執行次數最多的一段代碼 2.加法法則：總復雜度等于量級最大的那段代碼的復雜度 -- max 原則 3.乘法法則：嵌套代碼的復雜度等于嵌套內外代碼復雜度的乘積 4.O(m+n)、O(m*n)法則 原則：'通常會忽略掉公式中的常量、低階、系數' ~~~ >[danger] ##### 只關注循環執行次數最多的一段代碼 ~~~ 1.大 O 復雜度表示無窮大漸近，因此是一種變化趨勢的表現，通常會忽略掉 公式中的常量、低階、系數，只需要記錄一個最大階的量級就可以了，因此 分析一個算法、一段代碼的時間復雜度的時候，也只關注'循環執行次數最多'的 那一段代碼就可以了 2.下面的案例中利用這個理論得出的公式是：T(n) = O(n) ~~~ ~~~ function cal(n) { let sum = 0 // 運行時間 1 個unit_time let i = 1 // 運行時間 1 個unit_time for(;i<=n;i++){ // 運行時間 n 個unit_time sum = sum + i // 運行時間 n 個unit_time } return sum } console.log(cal(10)) // 55 ~~~ >[danger] ##### 加法法則：總復雜度等于量級最大的那段代碼的復雜度 -- max 原則 ~~~ 1.通常遵循原則'忽略掉公式中的常量、低階、系數' 因此下面代碼第一段循環 '100'是個常量執行時間，跟n（'數據的規模的大小'）的規模無關因此可以忽略 '對第一條的解釋(極客時間中王爭老師對著段的解釋如下):' 即便這段代碼循環 10000 次、100000 次，只要是一個已知的數，跟 n 無關， 照樣也是常量級的執行時間。當 n 無限大的時候，就可以忽略。 盡管對代碼的執行時間會有很大影響，但是回到時間復雜度的概念來說， 它表示的是一個算法執行效率與數據規模增長的變化趨勢，所以不管常量的執行時間多大， 我們都可以忽略掉。因為它本身對增長趨勢并沒有影響。 '我的簡單理解：' 因為是常量是固定在哪里的，但是'n'（'數據的規模的大小'）是非固定的可能是十億百億， 如果是這些那想對比100，這個100完全可以忽略也遵循了'大 O 復雜度表示無窮大漸近' 2.當一段代碼中有多段代碼他們都和'n'（'數據的規模的大小'），這時候需要遵循的是： '總的時間復雜度等于量級最大的那段代碼的時間復雜度',用公式表示的話： 如果' T1(n)=O(f(n))；T2(n)=O(g(n))'那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n))) ,即也就是說取兩個中最大的作為代碼的時間復雜度表示 3.分析下面案例： T1(n) = O(n);T2(n) = O(n^2) 因此 T(n) = T1(n)+T2(n) = max(O(n),O(n^2) ) 最后得出：T(n) = O(n^2) ~~~ ~~~ function cal(n){ let sum1 = 0 let p = 1 // ---- 這段代碼開始 ---- // 100 是常量 和 可能是無窮的N相比可以忽略 // 因此不考慮在我們的時間復雜度中 for(;p<100;p++){ sum1+=p } // --- 這段代碼結束 --- let sum2 = 0 let q = 1 // ---- 這段代碼開始 ---- // 和 n 有關因此考慮在復雜度中 // 表達公式T(n) = O(n) for(;q<n;q++){ sum1+=q } // --- 這段代碼結束 --- let sum3 = 0 let i = 1 let j = 1 // ---- 這段代碼開始 ---- // 和 n 有關因此考慮在復雜度中 // 表達公式T(n) = O(n^2) for(;i<=n;i++){ for(;j<=n;j++){ sum3+=i*j } } // --- 這段代碼結束 --- return sum3+sum1+sum2 } ~~~ >[danger] ##### 乘法法則：嵌套代碼的復雜度等于嵌套內外代碼復雜度的乘積 ~~~ 1.下面代碼和上面的代碼n^2 哪里類似，這里就不用js的表現形式，直接使用了 '極客時間王爭老師的代碼' 2.下面的代碼看到后，先按照第一個法則'關注循環執行次數最多的一段代碼', 最多的就是'循環嵌套'，在按照第二個法則'總復雜度等于量級最大的那段代碼的復雜度 -- max 原則' 整段'cal'只有一段代碼，因此直接可以忽略，現在按照第三條'嵌套代碼的復雜度等于嵌套內外代碼復雜度的乘積' 外層代碼'n' 內層代碼也為'n',因此最后得出：T(n) = O(n^2) ~~~ ~~~ int cal(int n) { int ret = 0; int i = 1; for (; i < n; ++i) { ret = ret + f(i); // 循環嵌套 } } int f(int n) { int sum = 0; int i = 1; for (; i < n; ++i) { sum = sum + i; } return sum; } ~~~ >[danger] ##### O(m+n)、O(m*n)法則 ~~~ 1.我們剛才的加法法則是在兩段代碼都是受控制與一個變量，我們遵循max取最大，但是 兩段代碼的控制變量分別是用兩個'數據的規模的大小'的變量控制，例如下面的代碼中的m 和n 分別控制各自的數據規模這時候就不能用'max'方法去取，而是兩者求和，乘法不變還是 相乘 2.因此下面的公式為：T(m)+T(n) = O(f(m)+f(n)) ~~~ ~~~ int cal(int m, int n) { int sum_1 = 0; int i = 1; for (; i < m; ++i) { sum_1 = sum_1 + i; //T(m) = O(m) } int sum_2 = 0; int j = 1; for (; j < n; ++j) { sum_2 = sum_2 + j; // T(n) = O(n) } return sum_1 + sum_2; } ~~~ >[info] ## 常見時間復雜度 ~~~ 1.O(1): Constant Complexity: Constant 常數復雜度 2.O(log n): Logarithmic Complexity: 對數復雜度 3.O(n): Linear Complexity: 線性時間復雜度 4.O(n^2): N square Complexity平方 5.O(n^3): N square Complexity ?立? 6.O(2^n): Exponential Growth 指數 7.O(n!): Factorial 階乘 ~~~ [圖片來源極客時間](https://time.geekbang.org/column/article/40036)  >[danger] ##### 時間復雜度劃分 --- 多項式量級、非多項式（NP）量級 ~~~ 1.多項式量級——隨著數據規模的增長，算法的執行時間和空間占用統一呈 多項式規律增長 2.非多項式量級——隨著數據量n的增長，時間復雜度急劇增長，執行時間無 限增加 3.解釋：把時間復雜度為非多項式量級的算法問題叫做NP（Non- Deterministic Polynomial,非確定多項式）問題，當數據規模n越大時，非多 項式量級算法的執行時間會急劇增加，求解問題的執行時間會無線增長。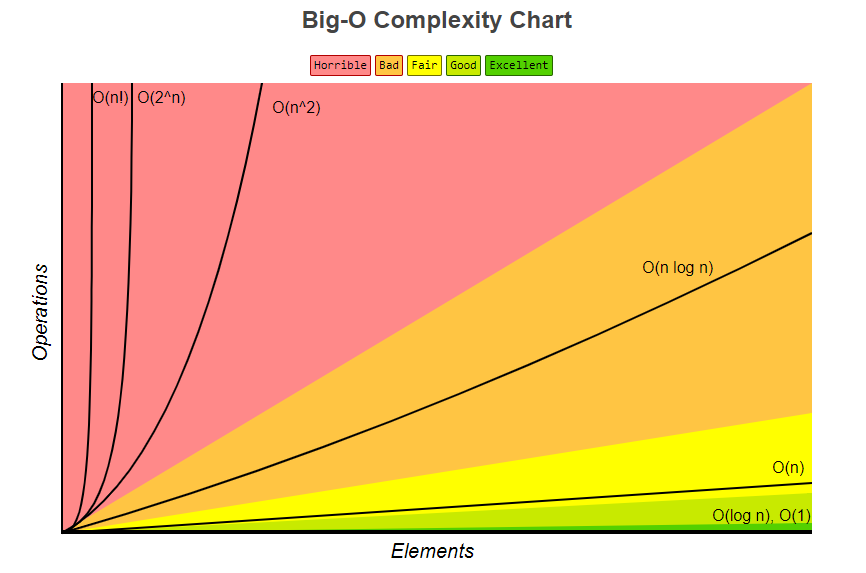所 以，'非多項式時間復雜度的算法其實是非常低效的算法' 4.通過下圖和下表也可看出來'非多項式量級'即使n的數據的規模的很小，他 的運算效率也是急速驟增的，因此'非多項式時間復雜度的算法其實是非常低效的算法' ~~~ * 附一張大O復雜度的圖[參考網站](https://www.bigocheatsheet.com/)  >[danger] ##### 將上面常見的進行歸類 | 多項式量級 | 非多項式量級 | | --- | --- | | O(1) 常量階 | O(2^n)指數 | | O(log n) 對數階 | O(n!): Factorial 階乘 | | O(n) 線性階 | | | O(nlog n) 線性對數階 | | | O(n^2)/O(n^3) 平方階/立方階 | | >[danger] ##### O(1) ~~~ 1.O(1) 只是常量級時間復雜度的一種表示方法，并不是指只執行了一行代碼。 2.簡單的說：只要代碼的執行時間不隨 n 的增大而增長，這樣代碼的時間復雜度我們都記作 O(1)。只要算法中不存在'循環語句'、'遞歸語句'，即使有成千上萬行的代碼，其時間復雜度也是Ο(1) 3.下面的代碼，即便有 3 行，它的時間復雜度也是 O(1），而不是 O(3)。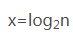 ~~~ ~~~ let name = 'wang' let age= '18' ~~~ >[danger] ##### O(logn)、O(nlogn) ~~~ 1.分析下面代碼執行，如果'n'(數據規模的大小)，為1則下面的代碼會走1次，n為2則會走2次， n為'3-6'走3次，如果取出他們最大節點可以表示為 ：2^0 = 1 / 2^1 =2 / 2^3 = 6 ，其中等號右邊 是下面代碼中變量'n'表示數據規模大小，左邊的次冪是代碼在這運行了幾次（也就是多少時間）， 假如代碼運行了'x' 次，那他所對應的數據規模'n'我們還是用n表示 即下面的代碼則為：2^x = n, 想求x的次數（這里x次數其實表示的是代碼運行時間），相求x（也就是運行時間），得到公式如下圖: 2.因此他時間復雜度則為T(n) = O(log2^n) ~~~  ~~~ i=1; while (i <= n) { i = i * 2; } ~~~ * 同理下面的代碼T(n) = O(log3^n) ~~~ i=1; while (i <= n) { i = i * 3; } ~~~