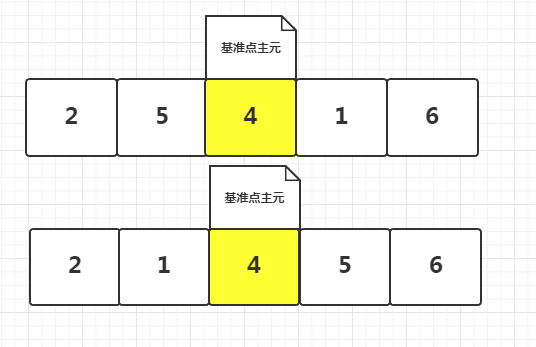
>[success] # js -- 快速排序 [很不錯的文章](https://juejin.im/post/6844904174014955527#heading-0) ~~~ 1.快速排序基本思想是：通過一趟排序將要排序的數據分割成獨立的'兩部分'，其中一部分的所有數據都比另外一部分的所有數據都要 '小'，然后再按此方法對這兩部分數據分別進行快速排序，整個排序過程可以遞歸進行，以此達到整個數據變成有序序列 2.根據上面的概念最重要的一點是要讓一組數據比另一組數據都'小'，為了做到這個，可以采用的思想方式是，找到這一組數據 中的任意一個值作為'基準'在快速排序中我們叫做'主元'，這個'主元'就會將數據分割成左右兩個部分，這兩個部分數據依次和'主元' 比較，最后比主元大的都在一側，小的在一側 ~~~  * 快排的模擬圖  >[info] ## 代碼實現方法 * 通用方法 ~~~ // 生成隨機數數組 function randomArray(max, min, len) { let randomNum = 0 const array = [] for (let i = 0; i < len; i++) { randomNum = Math.floor((Math.random() * (max - min + 1)) + min) array.push(randomNum) } return array } // const array = randomArray(1, 10, 5) const Compare = { LESS_THAN: -1, BIGGER_THAN: 1, EQUALS: 0 }; function defaultCompare(a, b) { if (a === b) { return Compare.EQUALS; } return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN; } ~~~ >[danger] ##### 代碼分析 * 這里引用的是《學習JavaScript數據結構與算法第3版》分析過程 ~~~ (1) 首先，從數組中選擇一個值作為'主元（pivot）'，也就是數組中間的那個值(也可以是隨機任意值)。 (2) 創建'兩個指針'（引用），左邊一個指向數組第一個值，右邊一個指向數組最后一個值。移 動左指針直到我們找到一個比主元大的值，接著，移動右指針直到找到一個比主元小的值，然后 交換它們，重復這個過程，直到左指針超過了右指針。這個過程將使得比主元小的值都排在主元 之前，而比主元大的值都排在主元之后。這一步叫作'劃分（partition）'操作。 (3) 接著，算法對劃分后的小數組（較主元小的值組成的子數組，以及較主元大的值組成的 子數組）重復之前的兩個步驟，直至數組已完全排序。 ~~~ 到這了還懵逼的話一定要讀開篇分享的文章 * 先實現分化的過程 ~~~ 1.首先會創建兩個指針'left','rihgt',選出'主元 piovt' 這里的主元使用數組中間元素 1.1.{1} -- 首先整個尋找過程只要兩個指針只要不出現交替越位結束，也就是'直到左指針超過了右指針' 1.2.先移動左側指針，移動的位置值和'主元'依次比較，當發現有比'主元'小的時候，開始移動右側指針依次和'主元' 比較，當發現有比'主元'大的時候停止查找，因為我們要形成'比主元小的值都排在主元之前，而比主元大的值都排在主元之后' ,這時候正好得到兩個位置處于相反地方兩個角標 1.3. {4} 這時候就要相互替換位置 ~~~ ~~~ function partition(array, left, right, compareFn = defaultCompare) { const pivot = array[Math.floor((right + left)) / 2] let i = left let j = right while (i <= j) { // {1} while (compareFn(array[i], pivot) === Compare.LESS_THAN) { // {2} i++ } while (compareFn(array[j], pivot) === Compare.BIGGER_THAN) { // {3} j-- } if (i <= j) { swap(array, i, j) //{4} i++; j-- } } return i } const array = [3, 5, 1, 6, 4, 7, 2] const partitionP = partition(array, 0, 4) console.log(partitionP) console.log(array) ~~~ * 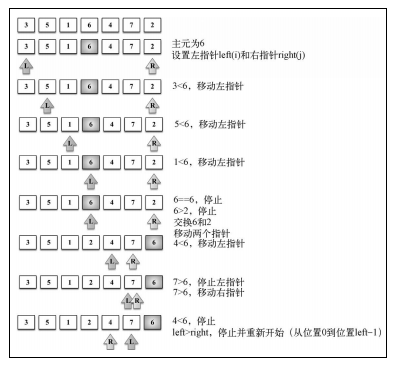如圖  * 快排代碼（還是暫時不懂） ~~~ function quickSort(array, compareFn = defaultCompare) { return quick(array, 0, array.length - 1, compareFn); }; function quick(array, left, right, compareFn) { let index; // {1} if (array.length > 1) { // {2} index = partition(array, left, right, compareFn); // {3} console.log(index, left, right, array) if (left < index - 1) { // {4} console.log(888) quick(array, left, index - 1, compareFn); // {5} } if (index < right) { // {6} quick(array, index, right, compareFn); // {7} } } return array; }; ~~~