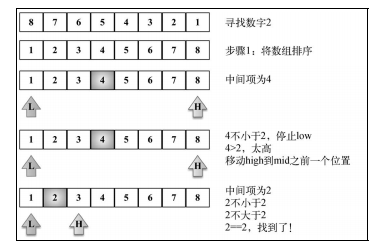
>[success] # 二分搜索 ~~~ 1.二分查找針對的是一個有序的數據集合，查找思想有點類似分治思想。 每次都通過跟區間的中間元素對比，將待查找的區間縮小為之前的一半， 直到找到要查找的元素，或者區間被縮小為 0 ~~~ * 引用一下《js數據結構與算法第三版圖》  >[danger] ##### 代碼實現 ~~~ 1.二分查找針對的是一個有序的數據集合，下面的案例我將快排的引用注釋掉了， 采用了寫死的一個案例方式，當然也可以直接用數組自帶的sort方法 ~~~ ~~~ const Compare = { LESS_THAN: -1, BIGGER_THAN: 1, EQUALS: 0 }; function lesserOrEquals(a, b, compareFn) { const comp = compareFn(a, b); return comp === Compare.LESS_THAN || comp === Compare.EQUALS; } function defaultCompare(a, b) { if (a === b) { return Compare.EQUALS; } return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN; } // 二分搜索需要先排序 // 查找的數組 要查找的值 function binarySearch(array,value) { const sortedArray = [1,2,3,6,8,24] ;// 這里才用快排 quickSort(array) let low = 0; let height = sortedArray.length-1; /** * 如果排序是從小到大 * 如果查詢的值大于中間項，說明要查找的值在右側，那我們最小指針就變成 mid +1 * 如果查詢的值小于中間項，說明要查找的值在左側，那我們最大指針就變成 mid -1 * 如果相等是要找值 位置 */ while(lesserOrEquals(low,height,defaultCompare)){ // 循環結束的條件當最小值和最大值錯位或者相等時候 const mid = Math.floor((low + height)/2) // 先找到中間位置 const element = sortedArray[mid] // 取出對應的中間值 if (defaultCompare(element, value) === Compare.LESS_THAN) { // {7} low = mid + 1; // {8} } else if (defaultCompare(element, value) === Compare.BIGGER_THAN) { // {9} height = mid - 1; // {10} } else { return mid; // {11} } } return -1 } console.log( binarySearch(1,8)) ~~~