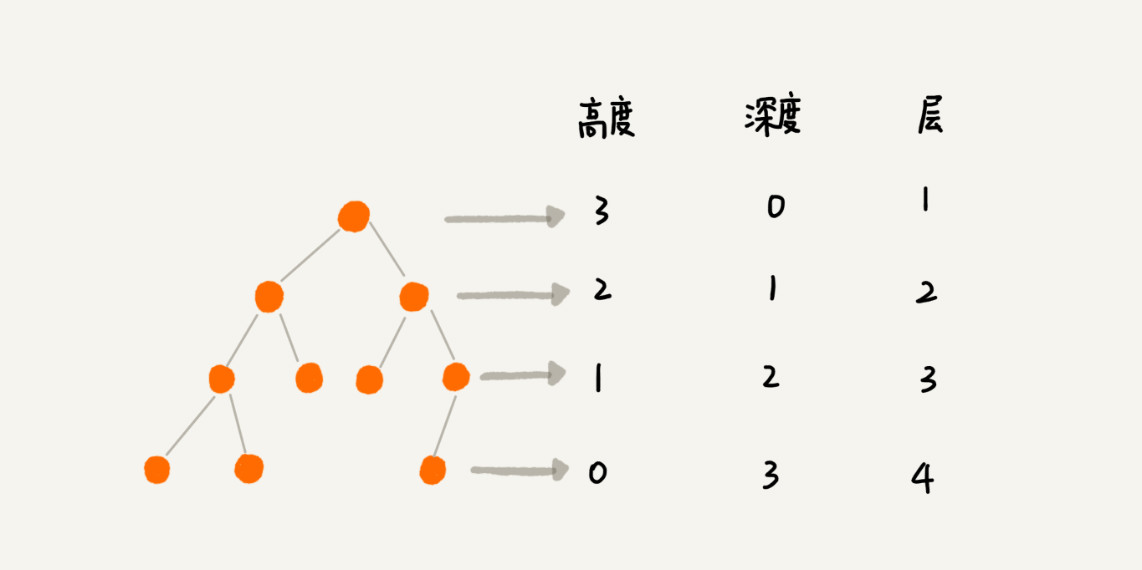
[TOC] >[success] # 樹 ~~~ 1.樹--是一種非順序結構 ~~~ >[info] ## 樹的相關術語 ~~~ 1.樹中每個元素我們叫做'節點'，用來連接相鄰'節點'之間的關系，叫做'父子節點' 2.每一個'樹結構'都包含一系列存在的父子關系節點，每個節點都有一個'父節點'(除了頂部第一個節點)， 以及0個或多個子節點 3.位于樹的頂部的節點叫作'根節點',也可以說把沒有父節點的節點叫作'根節點'。至少有一個子節點的節點叫 '內部節點'，沒有子元素的節點稱為'外部節點'又叫'葉子節點' 4.樹還有三個定義：'高度（Height）'、'深度（Depth）'、'層（Level）' ~~~ * 引用數據結構與算法文章的圖   >[success] # 二叉樹 和 二叉搜索樹 ~~~ 1.二叉樹中的節點最多只能有兩個子節點：一個是左側子節點，另一個是右側子節點。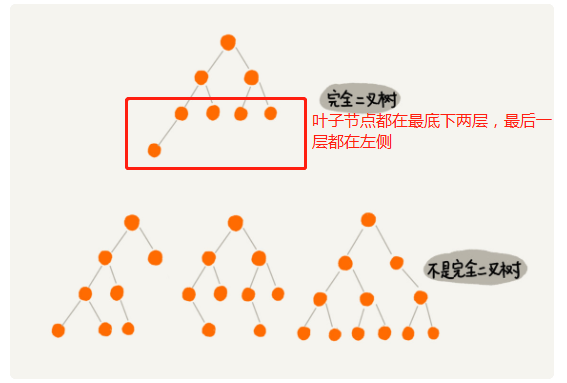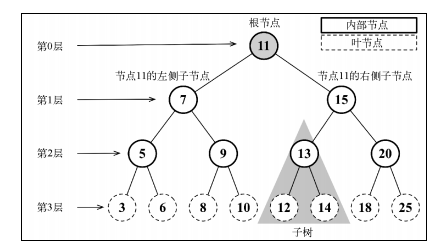注意這里說的 最多的意思是'二叉樹并不要求每個節點都有兩個子節點，有的節點只有左子節點，有的節點只有右子節點' 2.關于'滿二叉樹'，'完全二叉樹' 2.1.除了葉子節點之外，每個節點都有左右兩個子節點，這種二叉樹就叫作'滿二叉樹' 2.2.葉子節點都在最底下兩層，最后一層的葉子節點都靠左排列，并且除了最后一層，其他層的節點個數都要達到最 大，這種二叉樹叫作'完全二叉樹' 3.二叉搜索樹（BST）是二叉樹的一種，但是只允許你在左側節點存儲（比父節點）小的值， 在右側節點存儲（比父節點）大的值。 ~~~ * 完全二叉樹 和 不完全二叉樹  * 二叉搜索樹  >[info] ## 鏈式存儲法 -- 實現一個二叉樹 ~~~ 1.每個節點有三個字段，其中一個存儲數據，另外兩個是指向左右子節點的指針。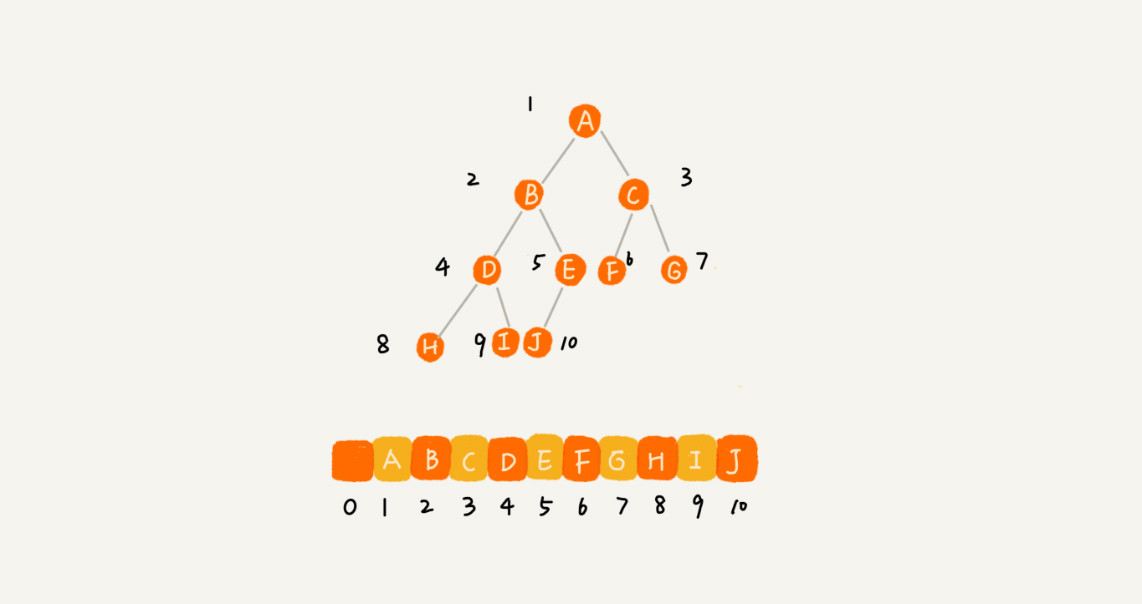我們只要拎住根節點，就可以通過左 右子節點的指針，把整棵樹都串起來 2.基于數組的'順序存儲法'把根節點存儲在下標 i = 1 的位置，那左子節點存儲在下標 2 * i = 2 的位置， 右子節點存儲在 2 * i + 1 = 3 的位置,因此可以得到一個規律：下標為 2 * i 的位置存儲的就是左子節點， 下標為 2 * i + 1 的位置存儲的就是右子節點。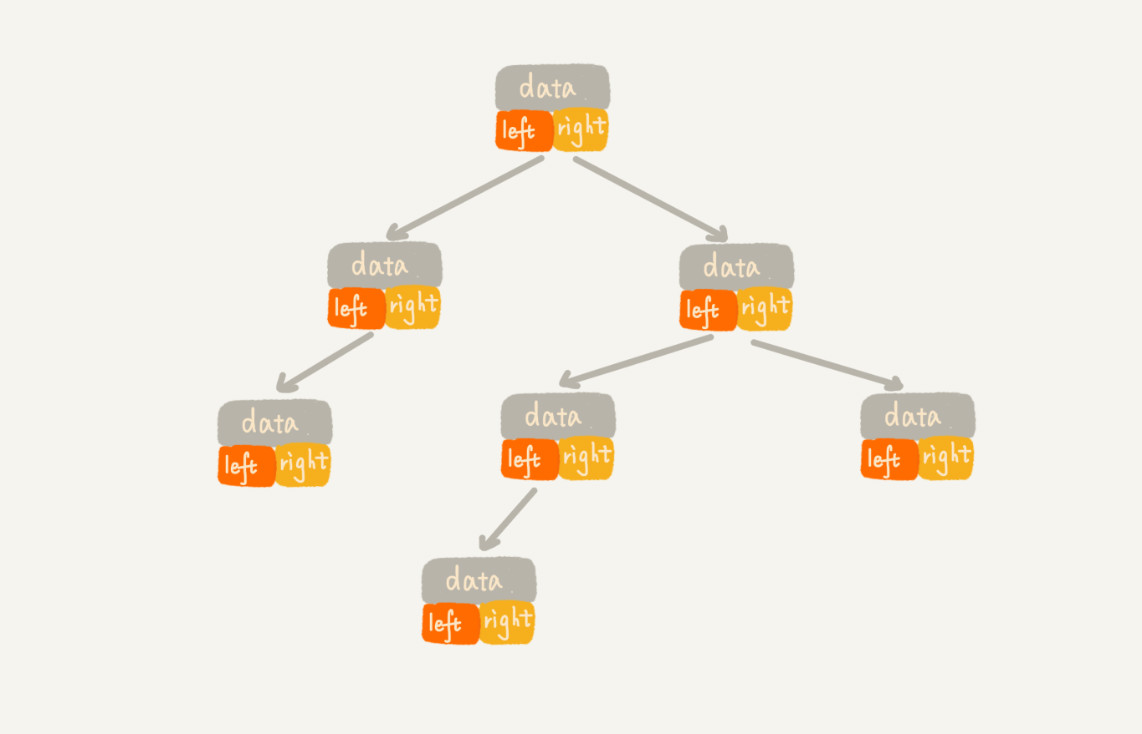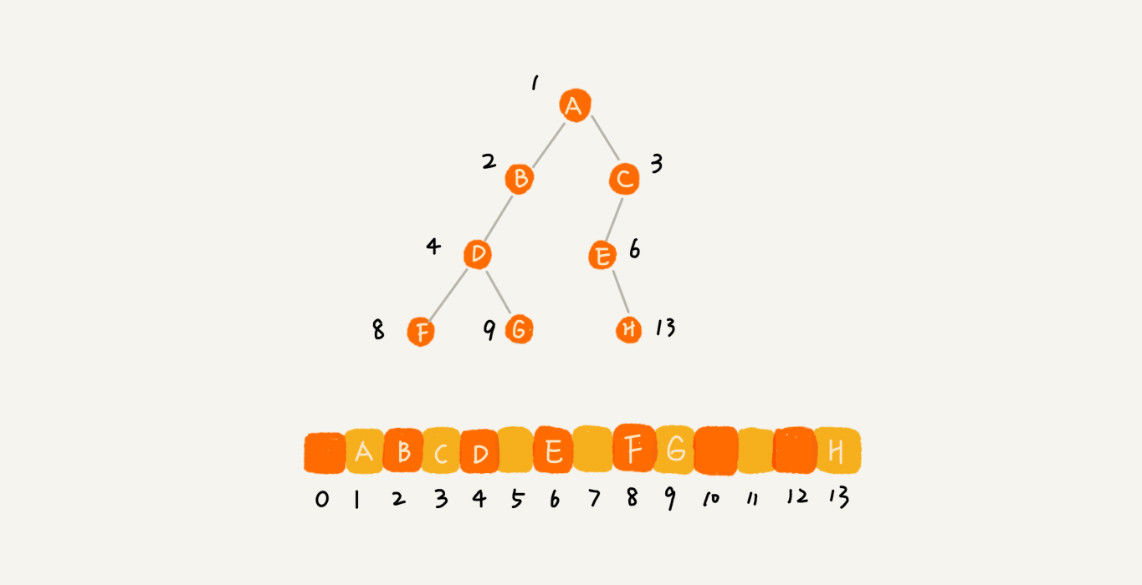反過來，下標為 i/2 的位置存儲就是它的父節點 ~~~ * 圖片來自數據結構與算法之美 -- 王爭老師  * 順序存儲法  * 當順序存儲法遇到不完全二叉樹的時候 ~~~ 1.如果某棵二叉樹是一棵完全二叉樹，那用數組存儲無疑是最節省內存的一種方式。 因為數組的存儲方式并不需要像鏈式存儲法那樣，要存儲額外的左右子節點的指針 2.也是為什么完全二叉樹要求最后一層的子節點都靠左的原因。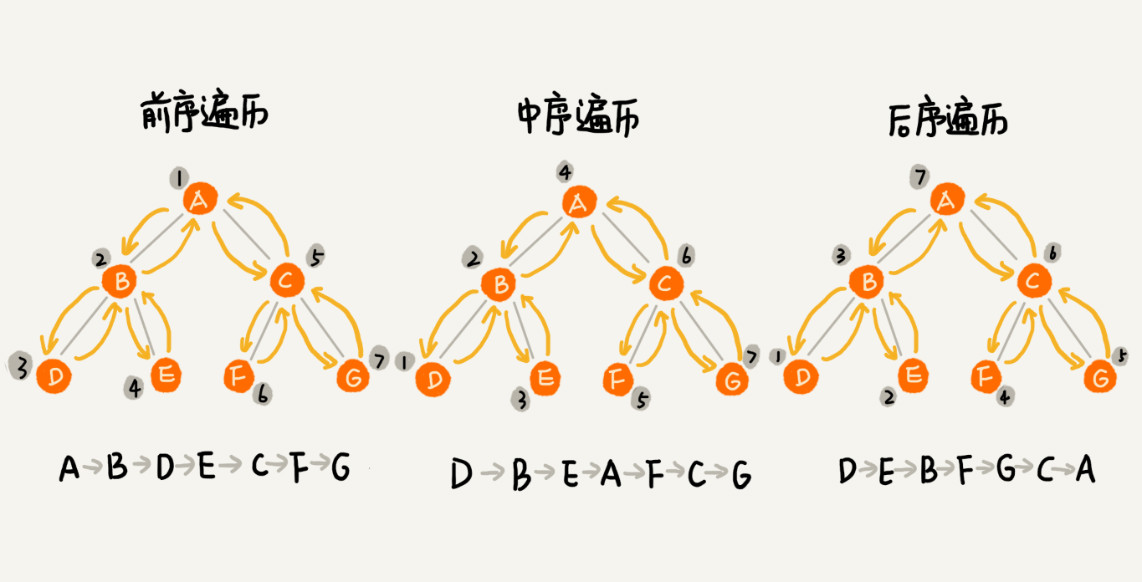 ~~~  >[info] ## 二叉樹的遍歷 ~~~ 1.經典的方法有三種，'前序遍歷'、'中序遍歷'和'后序遍歷' 2.1.'前序遍歷'是指，對于樹中的任意節點來說，先打印這個節點，然后再打印它的左子樹，最后打印它的右子樹。 2.2.'中序遍歷'是指，對于樹中的任意節點來說，先打印它的左子樹，然后再打印它本身，最后打印它的右子樹。 2.3.'后序遍歷'是指，對于樹中的任意節點來說，先打印它的左子樹，然后再打印它的右子樹，最后打印這個節點本身。 2.通過代碼實現 void preOrder(Node* root) { // 前 if (root == null) return; print root // 此處為偽代碼，表示打印root節點 preOrder(root->left); preOrder(root->right); } void inOrder(Node* root) { // 中 if (root == null) return; inOrder(root->left); print root // 此處為偽代碼，表示打印root節點 inOrder(root->right); } void postOrder(Node* root) { // 后 if (root == null) return; postOrder(root->left); postOrder(root->right); print root // 此處為偽代碼，表示打印root節點 } ~~~ * 如圖