>[success] # 數組 ~~~ 1.數組（Array）是一種線性表數據結構。它用一組'連續的內存空間'， 來存儲一組'具有相同類型的數據'。 2.線性表，線性表可以理解數據排成像一條線一樣的結構。每個線性 表上的數據最多只有前和后兩個方向。 3.注釋：js 數組不是傳統意義上的數組，采用的也不是線性表的形式， 在 JavaScript 中，數組是哈希映射，表現形式類似于鏈表，但如今編譯器 已經在為類型一致的數組分配連續的存儲空間了（這里還是有點疑問？？） 4.JS中的數組結構非常的簡單（已經是瀏覽器幫助我們進行封裝處理好的）可以存儲不同的數據類型值 數組容量伴隨存儲的內容自動縮放 5.數組這種結構： 優勢：基于索引直接進行查找和獲取，效率很高 弊端：進行中間插入和刪除操作時，性能非常低（數組塌陷和刪除中間項的優化） ~~~ [js數組中文，下面給出英文原文章地址](https://juejin.im/entry/59ae664d518825244d207196) 作者：[Paul Shan](https://link.juejin.im/?target=http%3A%2F%2Flink.zhihu.com%2F%3Ftarget%3Dhttp%253A%2F%2Fvoidcanvas.com%2Fauthor%2Fpaulshan%2F)原文：[Diving deep into JavaScript array - evolution & performance](https://link.juejin.im/?target=http%3A%2F%2Flink.zhihu.com%2F%3Ftarget%3Dhttp%253A%2F%2Fvoidcanvas.com%2Fjavascript-array-evolution-performance%2F) >[danger] ##### 線性表給數組帶來的優勢 ~~~ 1.如圖，圖片來自極客時間，通過圖片可以看出數組在內存中開辟一塊連續的、 大小相同的空間,用來存儲數據 2.因為'連續的內存空間和相同類型的數據',這兩個特性使得可以讓數據進行隨機訪問， 即他的查詢速度為O(1),也正是這個特性導致他的刪除和插入某個元素后還要保證其 內存的連續性，因此速度為O(n) 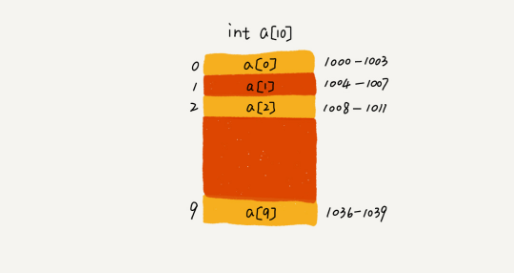3.以下圖為例該數組的長度為10，分配的空間地址為1000-1039，其中首項的地址為1000 即根據這個可以得到個簡單的公式'a[i]_address = base_address + i * data_type_size', 因此當我們取值的時候完全是腳標i這個常量控制因此復雜度為O(1),更準確地說：數組支持隨機訪問， 根據下標隨機訪問的時間復雜度為 O(1) 4.一下圖為例如果是刪除和插入，如果當插入或刪除的是是末尾，即直接在末尾加入對應的內存空間 地址和數據復雜度為O(1),那如果是頭部，則其他位置的數據的所有內存地址都需要進行平移則復雜度 為O(n),那他們的平均復雜度為O(n) ~~~  * js查詢和添加和刪除的例子 ~~~ 1.通過下面案例可以看出及時是js數組，像首位插入數據和刪除數據都O(n),如果頻繁對頭部做操作并且數據 量較大的時候還是要考慮這方面 ~~~ ~~~ var arr=[]; for(var i=0;i<=1000000;i++){ arr.push('abcdefghigk'+i); } console.time('arr'); arr.push(1) console.timeEnd('arr'); console.time('arr1'); arr.unshift('1') // 查詢耗時最多的 console.timeEnd('arr1'); console.time('arr2'); arr[1000000] console.timeEnd('arr2'); ~~~