>[success] # 棧
~~~
1.棧的應用場景一般是在編程語言的編譯器和內存中保存變量、方法調用,或者是瀏覽器歷史記錄返回按鈕
2.棧就像 一摞書,或者一摞盤子,在擺放這種一摞的物體的時候,我們一般都遵循,從下往上依次擺放,
從上往下依次拿出(這里排除你很厲害從中間抽取不倒)。這種存放得出一個結論'后進先出,先進后出',
這種結構就叫做'棧'
~~~
* 一摞書

>[info] ## 棧 和 數組區別
~~~
1.現在看來'棧'和'數組',感覺上棧看起來和數組很像,唯一不同的是數組沒有棧那么強的約束性質(棧只能'先進后出'),
數組反而更加靈活,數組對外暴露更多的操作接口,在操作上更加靈活自由,但是在操作上自然也會容易出錯。
~~~
>[danger] ##### 什么時候使用棧
~~~
1.當某個數據集合只涉及在一端插入和刪除數據,并且滿足后進先出、先進后出的特性,
我們就應該首選'棧'這種數據結構。
~~~
>[danger] ##### 如何實現棧
~~~
1.首先需,棧要滿足'先進后出原則',因此肯定需要可以入棧 和 出棧兩個操作,但是這兩個操作需要作用于棧頂,
(一摞的東西我們都是從頂部操作因此在棧頂)在棧頂插入一個數據和從棧頂刪除一個數據
2.這樣的話如果我們把數組進行二次封裝減少對外的暴露,讓其只能進行棧頂的操作,這樣通過數組實現的棧
叫'順序棧',用鏈表實現的棧,我們叫作'鏈式棧'
~~~
>[info] ## 時間復雜度
~~~
1.棧因為只能對棧頂進行操作,因此它的時間復雜度O(1),但類似java這類語言一般數組大小都是固定好的,所以
當我們操作的棧大小已經超出我們要存儲的內容的時候,數組需要擴容因此,時間復雜度在這個時候就會變成O(n)
,但是只有這個瞬間是O(n) 整體的平均復雜度依舊是O(1)
~~~
>[info] ## 瀏覽器后退棧的應用
~~~
1.當你依次訪問完一串頁面 a-b-c 之后,點擊瀏覽器的后退按鈕,就可以查看之前瀏覽過的頁面 b 和 a。當你后退到頁
面 a,點擊前進按鈕,就可以重新查看頁面 b 和 c。但是,如果你后退到頁面 b 后,點擊了新的頁面 d,那就無法再通
過前進、后退功能查看頁面 c 了
~~~
>[danger] ##### 實現原理
[參考地址](https://time.geekbang.org/column/article/41222)
~~~
1.X 和 Y,我們把首次瀏覽的頁面依次壓入棧 X,當點擊后退按鈕時,再依次從棧 X 中出棧,
并將出棧的數據依次放入棧 Y
~~~
~~~
1.比如你順序查看了 a,b,c 三個頁面,我們就依次把 a,b,c 壓入棧,這個時候,兩個棧的數據就是這個樣子
~~~
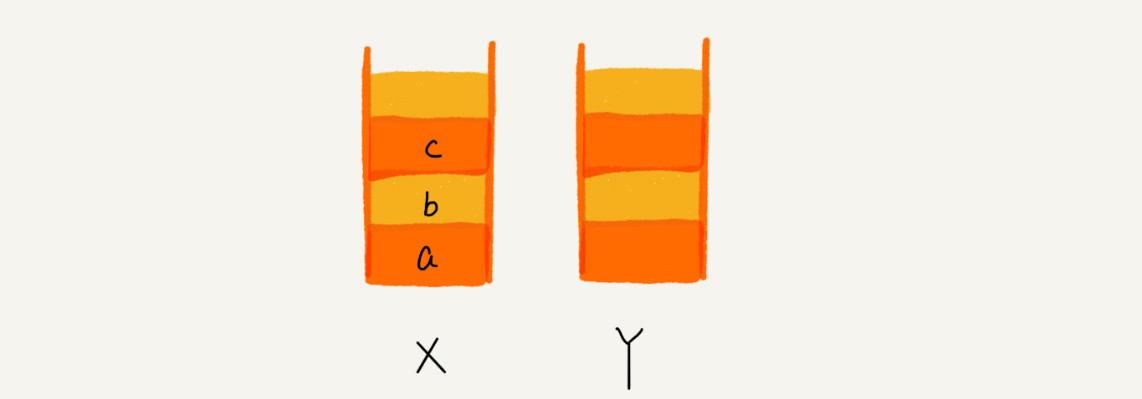
~~~
1.當你通過瀏覽器的后退按鈕,從頁面 c 后退到頁面 a 之后,我們就依次把 c 和 b 從棧 X 中彈出,并且依次放入到棧
Y。這個時候,兩個棧的數據就是這個樣子:
~~~
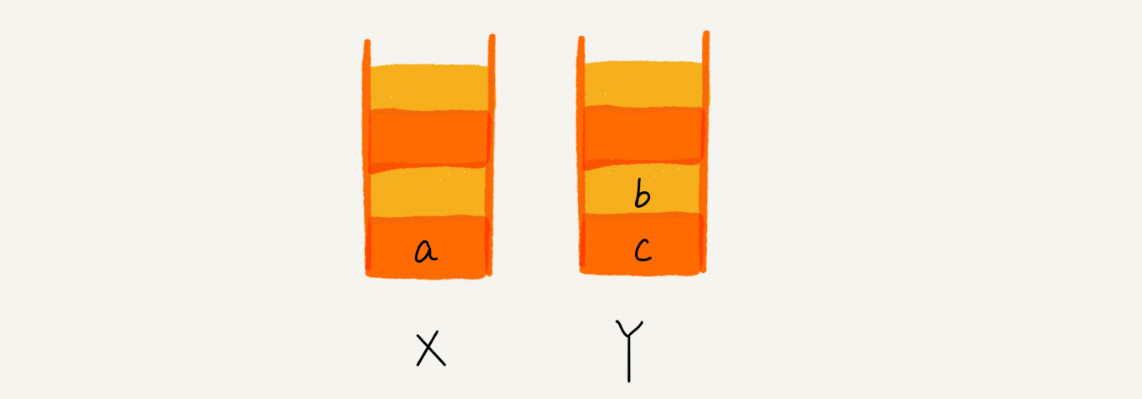
~~~
1.這個時候你又想看頁面 b,于是你又點擊前進按鈕回到 b 頁面,我們就把 b 再從棧 Y 中出棧,放入棧 X 中。此時兩
個棧的數據是這個樣子
~~~
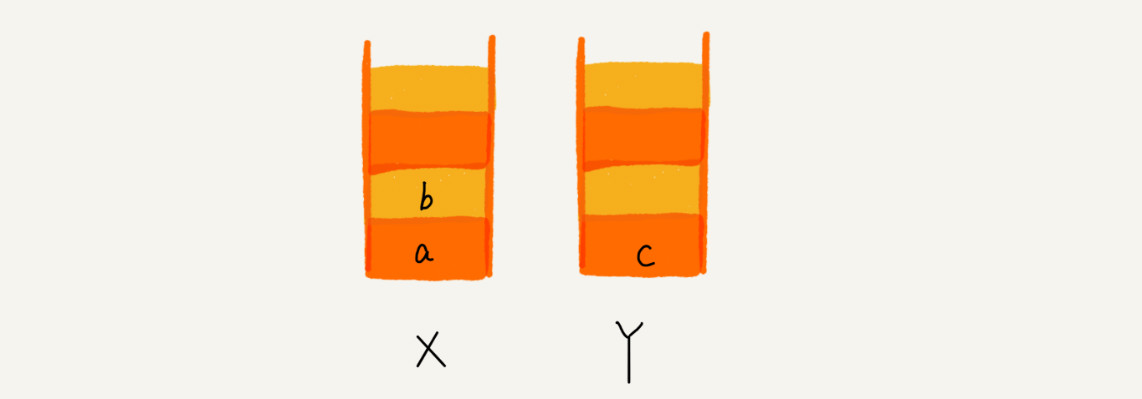
~~~
1.這個時候,你通過頁面 b 又跳轉到新的頁面 d 了,頁面 c 就無法再通過前進、后退按鈕重復查看了,所以需要清空
棧 Y。此時兩個棧的數據這個樣子
~~~
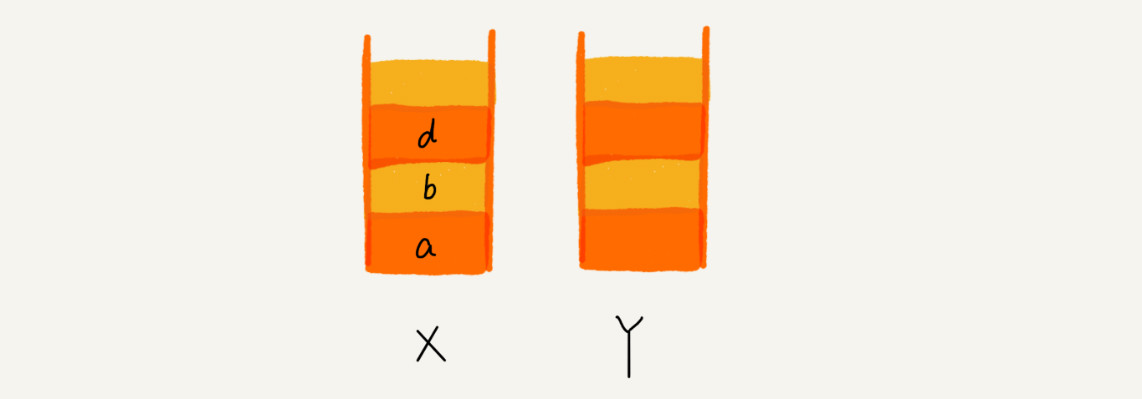
- 接觸數據結構和算法
- 數據結構與算法 -- 大O復雜度表示法
- 數據結構與算法 -- 時間復雜度分析
- 最好、最壞、平均、均攤時間復雜度
- 基礎數據結構和算法
- 線性表和非線性表
- 結構 -- 數組
- JS -- 數組
- 結構 -- 棧
- JS -- 棧
- JS -- 棧有效圓括號
- JS -- 漢諾塔
- 結構 -- 隊列
- JS -- 隊列
- JS -- 雙端隊列
- JS -- 循環隊列
- 結構 -- 鏈表
- JS -- 鏈表
- JS -- 雙向鏈表
- JS -- 循環鏈表
- JS -- 有序鏈表
- 結構 -- JS 字典
- 結構 -- 散列表
- 結構 -- js 散列表
- 結構 -- js分離鏈表
- 結構 -- js開放尋址法
- 結構 -- 遞歸
- 結構 -- js遞歸經典問題
- 結構 -- 樹
- 結構 -- js 二搜索樹
- 結構 -- 紅黑樹
- 結構 -- 堆
- 結構 -- js 堆
- 結構 -- js 堆排序
- 結構 -- 排序
- js -- 冒泡排序
- js -- 選擇排序
- js -- 插入排序
- js -- 歸并排序
- js -- 快速排序
- js -- 計數排序
- js -- 桶排序
- js -- 基數排序
- 結構 -- 算法
- 搜索算法
- 二分搜索
- 內插搜索
- 隨機算法
- 簡單
- 第一題 兩數之和
- 第七題 反轉整數
- 第九題 回文數
- 第十三題 羅馬數字轉整數
- 常見一些需求
- 把原始 list 轉換成樹形結構
