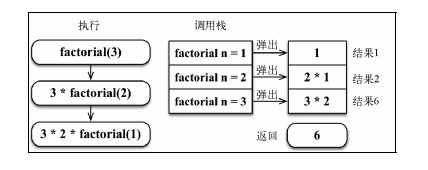
[TOC] js 優化遞歸使用尾調用優化 >[success] # 遞歸階乘 ~~~ 1.求5*4*3*2*1 的問題，用遞歸來解決三步走 1.1.分解成各個小部分 5 * fn(4) 參數n = 5-1 5 * (4*fn(3)) 參數n = 4-1 5 * 4 * (3*fn(2)) 參數n = 3-1 5 * 4 * 3 * (2*fn(1)) 參數n =2-1 1.2.推到成遞歸公式 fn(n) = n*fn(n-1) ,且fn(1) = 1 1.3.終止條件 fn(1) = 1 ~~~ >[danger] ##### 代碼 ~~~ 1.遞歸是棧的結構表現，所以它'遞'的過程是在做壓棧，'歸'的過程在做出棧，其實本質，先算的是 終止條件，然后在依次向上傳遞 2.如圖一，通過瀏覽器的控制臺可以更形象的看出這個過程 ~~~ ~~~ // 遞歸階乘 求 5*4*3*2*1 // 先拆分 5 * fn(4) 參數n = 5-1 // 5 * (4*fn(3)) 參數n = 4-1 // 5 * 4 * (3*fn(2)) 參數n = 3-1 // 5 * 4 * 3 * (2*fn(1)) 參數n =2-1 // 現在就是一個壓棧的過程，從5*fn(4)先進，依次壓棧直到最后 fn(1)，執行的時候 // 出棧時候從fn(1) 開始執行，因此為什么要有終止條件也可以理解了 function factorial(n){ console.trace() // 記錄堆棧 // 歸的過程 -- 墻相當于 乘到了1 if(n===1 || n===0){ return 1 } console.log(n) // 調用 -- 傳遞的過程 return n * factorial(n-1) } factorial(5) ~~~ * f12 打斷點也可發現遵循棧的思路先進后出  * 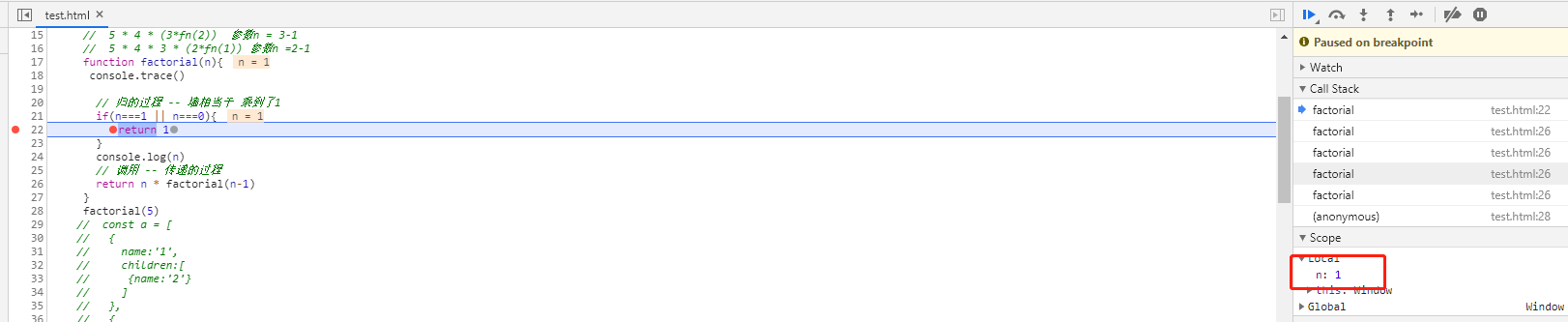運行圖解  >[success] # 斐波那契數列 ~~~ 0，1，1，2，3，5，8，13，21 ~~~ >[danger] ##### 不用遞歸 ~~~ // 斐波那契數列 function fibonacciIterative(n){ if(n < 1) return 0 if(n <=2) return 1 let fib2 = 0 let fib1 = 1 let fibN = 0 for(let i =3;i<=n;i++){ fibN = fib1 + fib2 fib2 = fib1 fib1 = fibN } return fibN } ~~~ >[danger] ##### 使用遞歸 ~~~ // 斐波那契數列 function fibonacciIterative(n){ if(n < 1) return 0 // 結束條件 if(n <=2) return 1 // 結束條件 return fibonacciIterative(n-2) + fibonacciIterative(n-1) // 遞歸公式 fn(n) = fn(n-1)+fn(n-2) } ~~~ >[success] # 減少重復遞歸 -- 記憶化方法 ~~~ 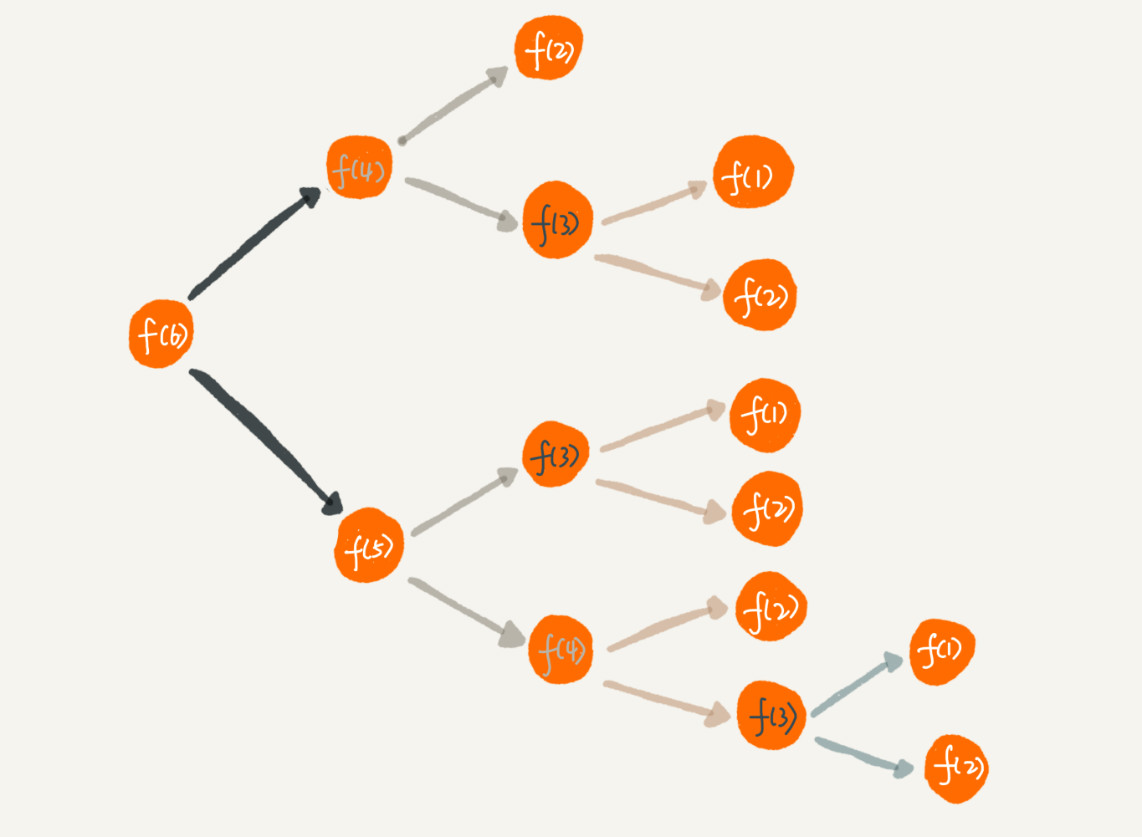1.向求解斐波那契數列時候，將求解過程圖形化，可以看出，有些已經 求過的結點我們還會反復在求，如果把這些一求過的數存起來直接用，也會 提高效率 ~~~  >[danger] ##### 代碼 ~~~ function fibonacciMemoization(n) { const memo = [0, 1]; const fibonacci = (n) => { if (memo[n] != null) return memo[n]; return memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo); }; return fibonacci(n); } ~~~