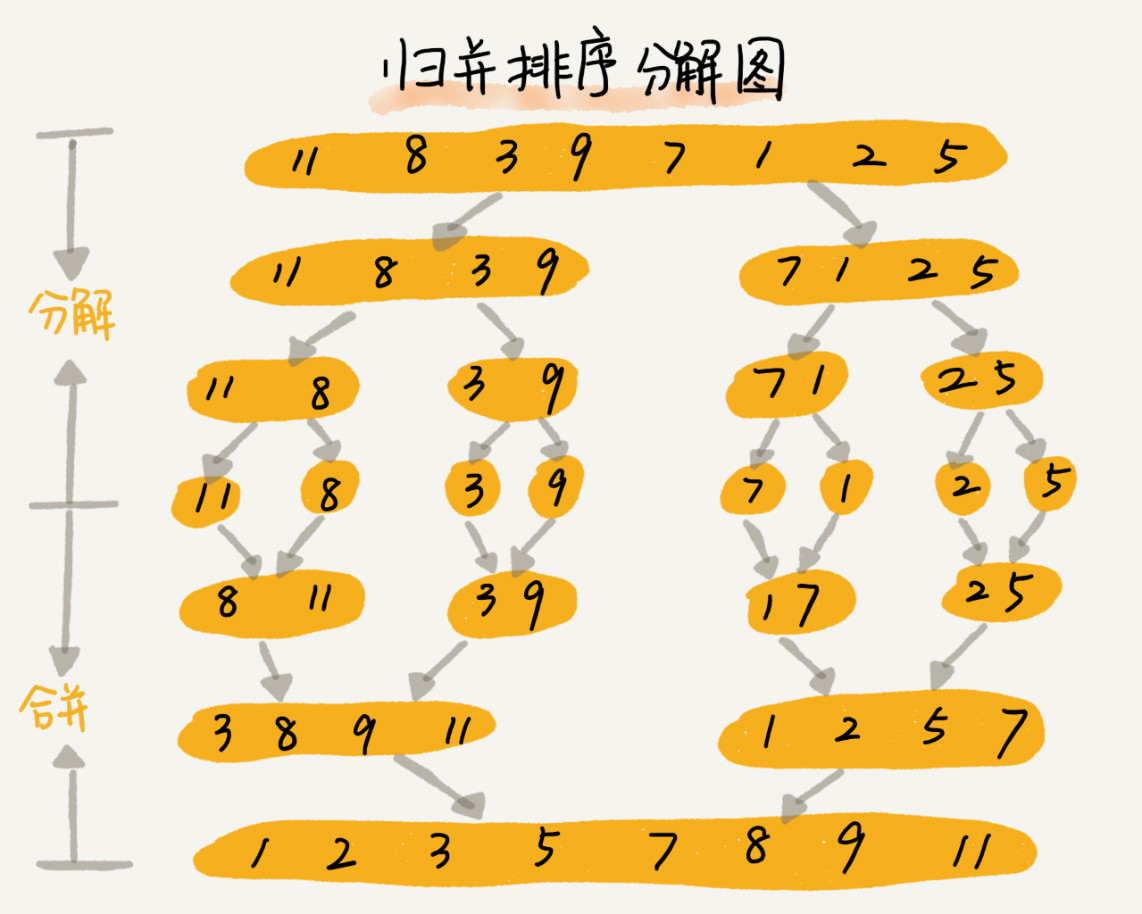
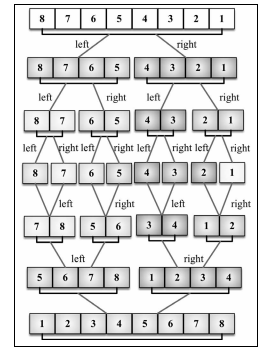
>[success] # 歸并算法（還要在好好理解暫時略過） [很不錯的文章](https://juejin.im/post/6844904169589964807#heading-0) ~~~ 1.'歸并算法'：將原始數組切分成較小的數組，直到每個小數組只有一個位置，接著將小數組歸并成較大的數組， 直到最后只有一個排序完畢的大數組 2.如圖和定義分析首先需要兩步（因此我們需要兩個方法）： 2.1.第一個方法是分解需要將大數組不停的切割，直到每個項變成單獨一個，這個過程需要一個遞歸方法 2.2.第二個方法需要合并在比較完成后，將每個小塊依次比較最后形成一個大數組 3.上面用到的思想叫'分治思想'。將一個大問題分解成小的子問題來解決。小的子問題解決了，大問題也就解決了 ~~~  * 引用《數據結構與算法之美》王爭老師的圖  * 引用《javasprict 數據結構與算法》  >[info] ## 代碼實現 * 通用方法 ~~~ // 生成隨機數數組 function randomArray(max, min, len) { let randomNum = 0 const array = [] for (let i = 0; i < len; i++) { randomNum = Math.floor((Math.random() * (max - min + 1)) + min) array.push(randomNum) } return array } // const array = randomArray(1, 10, 5) const Compare = { LESS_THAN: -1, BIGGER_THAN: 1, EQUALS: 0 }; function defaultCompare(a, b) { if (a === b) { return Compare.EQUALS; } return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN; } ~~~ >[danger] ##### 代碼分析 ~~~ 1.跟上面的分析一樣需要兩個方法第一個方法是分，也就是將數組分成最小單個為一組數組方法'mergeSort', 第二個就是將這些細分維度的數組依次比較合并'merge'方法，這里要注意的是'merge'方法里面有個暫存 新排序的數組 2.'mergeSort'方法比較好理解就是一個遞歸過程，這個過程需要將數組項不停拆分成左右結構， 遞歸的過程之前章節有分析過，要有一個終止條件這個條件就是'歸'，這個方法中的'歸'就是將數組 已經拆分成最小結構單獨項對應代碼中'array.length>1' 判斷條件 3.'merge'這個合并方法比較復雜這里拆分了三個結構依次對應{1},{2},{3} 3.1.'{1},{2}' -- 數組會被拆分，這里拿出某一刻的拆分，來對這一部分的代碼做解釋， 當左側拆分為'[3,6]',右側拆分為'[4,5,8]'，這時候需要邏輯是右側數組中的內容依次和左側數組中的內容 比較，比較完后會放到'merge'方法中的一個暫存數組，形成數據狀態為[3,4,5,6]。這里要注意的是{2}， 首先明確 'i'和'j' 不會同時自增，他們是根據比較狀態來決定那個自增，這樣就可以形成依次比較 3.2.'{3}' -- 當上面將整體數組排序后，將最后剩余值添加到數組末尾 4.這里來個總結版本：歸并首先采用的是'分治思想',這類思想很像遞歸，把大問題拆成小問題，小問題 解決了，大問題最后也就跟著解決了，簡單的說就是'逐一擊破' 4.1.'逐一擊破'我們要做的就是將數組不停切割，切割的原則是數組長度的二分之一，這種切割就會產生 兩個數組，我們要做是在切割最小單位及左右數組里面都只有一個值時候開始我們的比較 4.2.'在選排序' 和 '插入排序'的時候這兩者用的是，將數組分成兩個區域'已排序'和'為排序'兩個區域， '歸并排序' 我們將不采用這種結構劃分，我會用另外一個數組來存儲這些排序后的數據 4.3.上兩步我們做好了'拆分'和'比較后值應該存放的位置'，現在要解決如何比較左右兩個數組值舉個例子, 現在有個數組'[6,7,8,1,3,2,5]',經過拆分后他將呈現效果是： [ 7 ] [ 8 ] [ 6 ] [ 7, 8 ] [ 1 ] [ 3 ] [ 2 ] [ 5 ] [ 1, 3 ] [ 2, 5 ] [ 6, 7, 8 ] [ 1, 3, 2, 5 ] 現在要解決的是兩個數組之間值的比較，這里采用指針的解決思路，分別有兩個指針，最初位置分別為兩個 相互比較數組其實位置 4.4.較兩個指針所指向的元素，選擇相對小的元素放入到合并空間就是我們在4.2位置創建數組， 并移動指針到下一位置，一直重復這個過程，直到某一指針達到序列尾，將另一序列剩下的所有 元素直接復制到合并序列尾 5.整個歸并解決思路： 5.1.申請空間，使其大小為兩個已經排序序列之和，該空間用來存放合并后的序列； 5.2.設定兩個指針，最初位置分別為兩個已經排序序列的起始位置； 5.3.比較兩個指針所指向的元素，選擇相對小的元素放入到合并空間，并移動指針到下一位置； 5.4.重復步驟 3 直到某一指針達到序列尾； 5.5.將另一序列剩下的所有元素直接復制到合并序列尾。 ~~~ ~~~ //1.將數組進行切割變成只用單獨一項 function mergeSort(array,compareFn = defaultCompare){ // 如果數組只有一項就不用進行比較了 // 這是一個遞歸方法因此 這判斷條件相當于'歸' 結束遞歸過程 if(array.length>1){ const {length} = array const middle = Math.floor(length / 2) const left = mergeSort(array.slice(0,middle),compareFn) const right = mergeSort(array.slice(middle,length),compareFn) // console.log(left,right) // 第二步需要合并將這些單個項進行合并比較 array= merge(left,right,compareFn) } // console.log(array,222) return array } function merge(left, right, compareFn) { let i = 0; let j = 0; const result = []; console.log(left,'left'); console.log(right,'right'); while (i < left.length && j < right.length) { // {1} result.push( compareFn(left[i], right[j]) === Compare.LESS_THAN ? left[i++] : right[j++] // {2} ); } console.log(result,2); const a = result.concat(i < left.length ? left.slice(i) : right.slice(j)); // {3} console.log(a,2222); return a } // console.log(array) console.log(mergeSort([3,6,4,5,8])) ~~~ * 打印效果