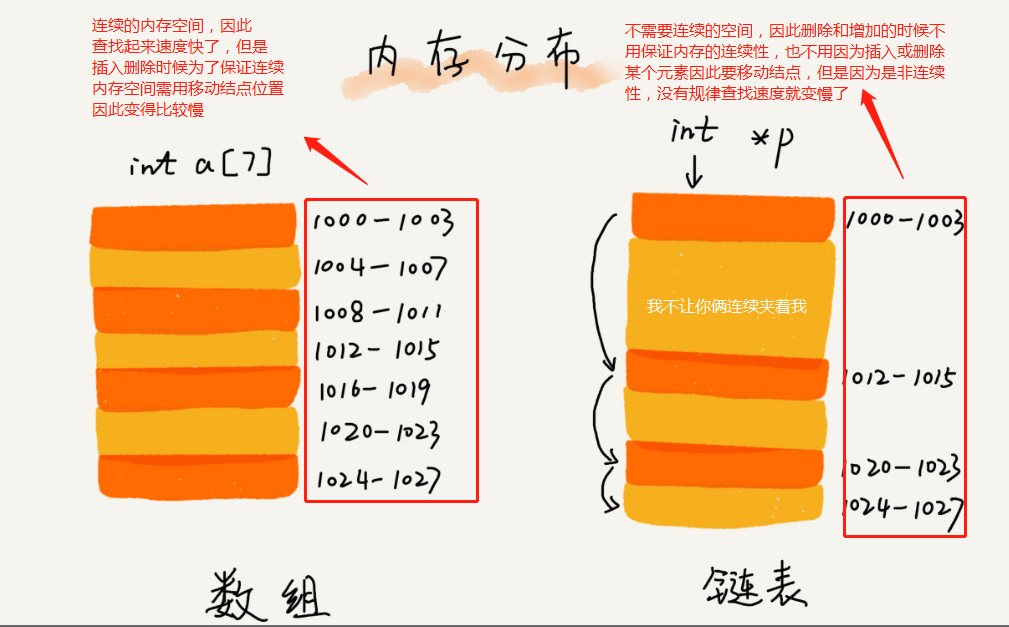
>[success] # 鏈表 ~~~ 1.了解鏈表前還需要再次看一下數組的概念，在類似java的語言中'數組的大小在生命使用的時候是固定' ，因此數組需要一塊'連續的內存空間'來儲存。因此產生的問題如下： 1.1.如果申請內存大小為'100MB'大小數組，由于'連續的內存空間'沒有這么大數組申請失敗 1.2.從數組起點或者中間位置插入或移除所需時間成本較高，因為數組要保證內存數據的連續性，因此 需要做大量的數據搬移，也就是數組插入和刪除的復雜度為O(n)， 2.鏈表是用來存儲有序的元素集合，但它'不需要連續的內存空間'，也就是說鏈表中的元素在內存中 '并不是連續放置的，它是通過'指針'將一組零散的內存塊串聯起來使用，因此它的好處： 1.1.使用時'不在受連續的內存空間'這個問題所影響，也就是如果需要'100MB'的內存空間只要剩余空間加來 有這么大就行 1.2.'不在需要因為要保持內存的連續性而搬移結點'簡單地說因為'鏈表空間不是連續的'，所以他的插入和刪除 速度非常快，時間復雜度表示'O(1)' 3.數組在查找的時候時間復雜度為'O(1)' 但是在插入和刪除的時候時間復雜度'O(n)',鏈表在插入和刪除的時候 時間復雜度為'O(1)',在查找的時候時間復雜度為'O(n)',這都是因為彼此的特性導致的 ~~~ >[info] ## 使用圖進一步說明 * 圖片來自極客時間數據結構與算法之美（結構來說明）  * 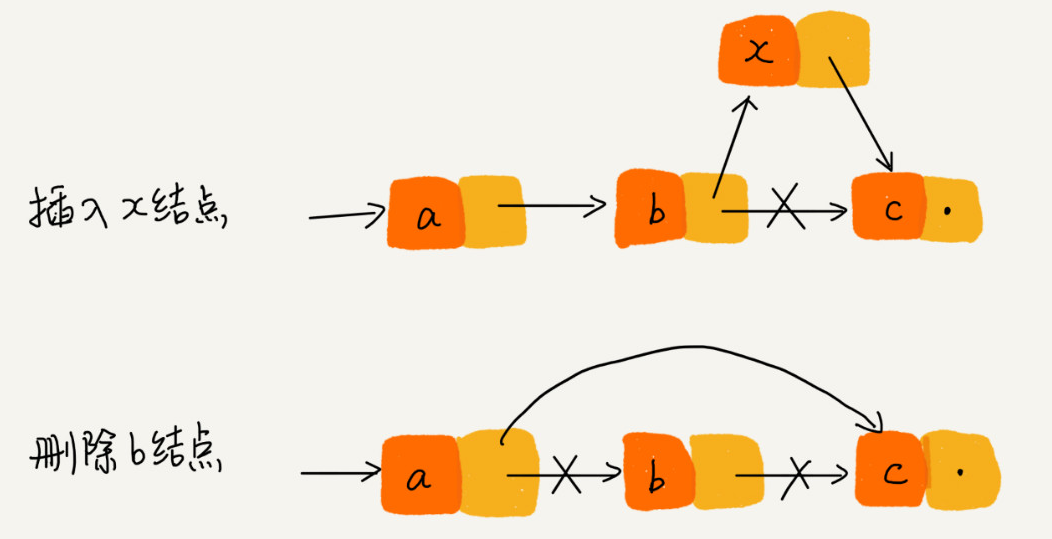圖片來自極客時間數據結構與算法之美（來說明為什插入和刪除速度快） ~~~ 1.插入的時候只要讓b 和 c 結點沒有關系，讓b結點指向新插入的x節點，讓x結點指向c節點 2.刪除的時候讓b節點和 a，c節點一點關系沒有即可 ~~~  >[danger] ##### 單鏈表 ~~~ 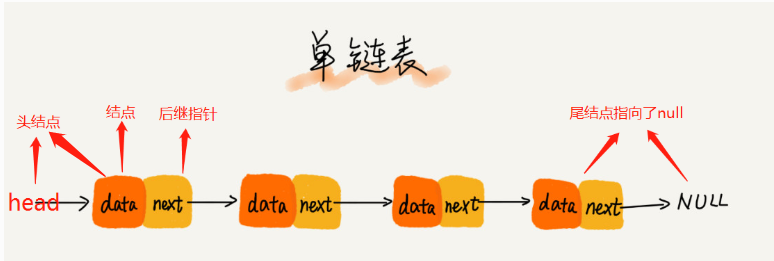1.首先是鏈表的構成可以理解成：每個元素由一個存儲元素本身的節點和一個指向下一個元素的引用 （也稱指針或鏈接）組成。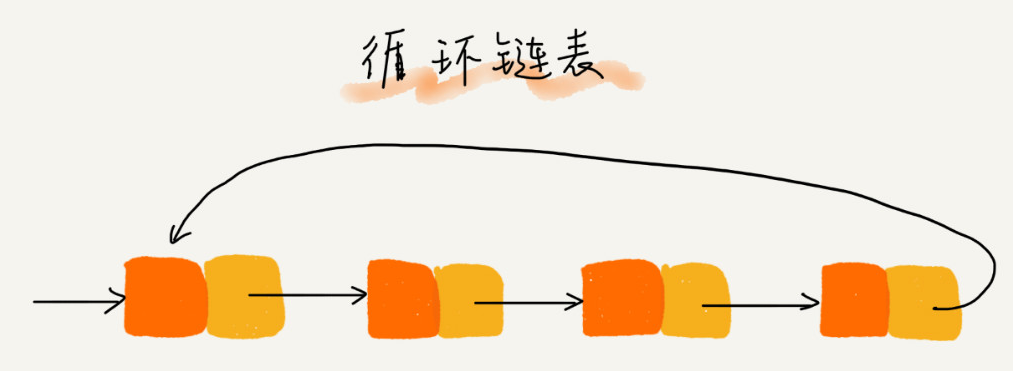 2.把內存塊稱為'結點'，把當前結點和下一結點連接的指針叫'后繼指針next' 3.由于鏈表內存空間不是連續的因此你訪問的時候只能從'頭'開始訪問，這個第一個結點叫'頭結點'， 把最后一個節點叫做'尾結點' 3.1 '頭結點做的是用來記錄鏈表的基地址' 簡單的說你要查找鏈表中某個元素你給先找到這個 鏈表，在根據每個'結點'互相連接的關系找到你想查找的'結點' 3.2'尾結點指向的是一個空地址null，js是undefined'用來表示鏈表到頭了 ~~~ * 圖片來自極客時間數據結構與算法之美 ~~~ 1.因此通過圖可以知得知，想查找鏈表中某個結點位置，需要從頭結點開始一個一個結點找直到找到 要找的結點 ~~~  >[danger] ##### 循環鏈表 ~~~ 1.循環鏈表就是將鏈尾連接到鏈頭，也就是說'尾結點指向的不在是null而是頭結點'，形成首尾相連的效果 2.需要處理環形結構時候可以使用'循環鏈表' ~~~ * 圖片來自極客時間數據結構與算法之美  >[danger] ##### 雙向鏈表 ~~~ 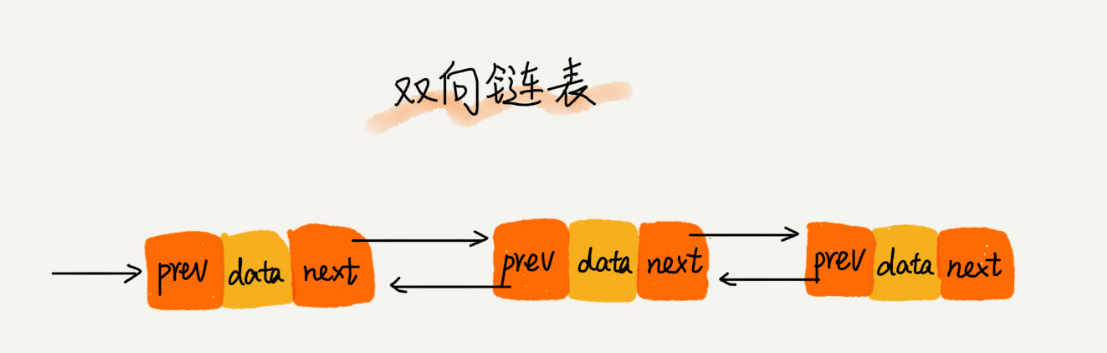1.雙向鏈表相對于單向鏈表來說'鏈接是雙向的：一個鏈向下一個元素， 另一個鏈向前一個元素' 2.就是說雙向鏈表和單鏈表相比不止有'后繼指針next' 它還有一個'前驅指針prev' 3.因為雙向鏈表的結構導致他獨有的特性： 3.1.因為有兩個指針因此它的沒存空間占用會更多，浪費儲存空間 3.2.但可以支持雙向遍歷，這樣也帶來了雙向鏈表操作的靈活性舉個例子： 在單向鏈表中，如果迭代時錯過了要找的元素，就需要回到起點，重新開始迭代。這是雙向 鏈表的一個優勢。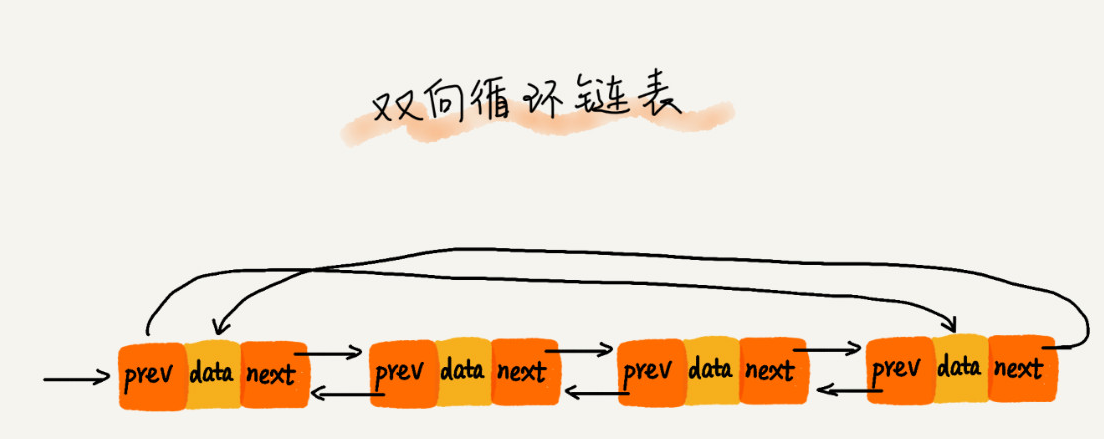 ~~~ * 圖片來自極客時間數據結構與算法之美  >[danger] ##### 雙向循環鏈表 ~~~ 1.循環鏈表可以像鏈表一樣只有單向引用，也可以像雙向鏈表一樣有雙向引用。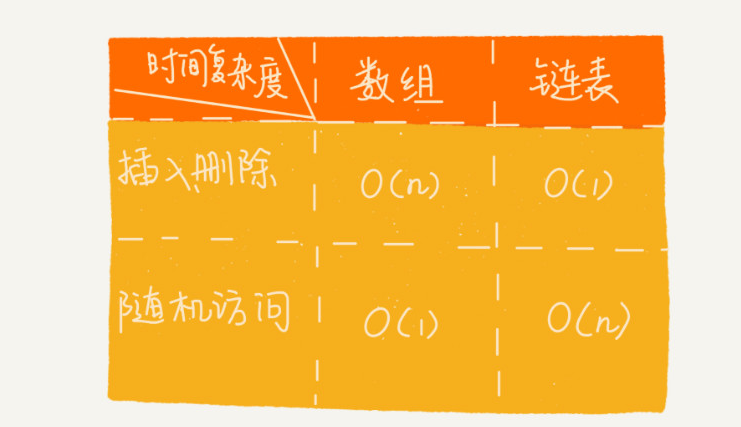循環鏈表和鏈 表之間唯一的區別在于，最后一個元素指向下一個元素的指針不是引用 null，而是指向第一個元素（head）， ~~~ * 圖片來自極客時間數據結構與算法之美  >[success] # 數組和鏈表的性能分析 >[danger] ##### 兩者的區別 ~~~ 1.數組：插入、刪除的時間復雜度是O(n)，隨機訪問的時間復雜度是O(1)。 2.鏈表：插入、刪除的時間復雜度是O(1)，隨機訪問的時間復雜端是O(n)。 3.鏈表的內存空間消耗更大，因為需要額外的空間存儲指針信息。 4.對鏈表進行頻繁的插入和刪除操作，會導致頻繁的內存申請和釋放，容易造成內存碎片， 如果是Java語言，還可能會造成頻繁的GC（自動垃圾回收器）操作。 ~~~ * 圖片來自極客時間數據結構與算法之美  >[danger] ##### 選擇兩者誰 ~~~ 1.數組簡單易用，在實現上使用連續的內存空間，可以借助CPU的緩沖機制預讀數組中的數據， 所以訪問效率更高，而鏈表在內存中并不是連續存儲，所以對CPU緩存不友好，沒辦法預讀。 如果代碼對內存的使用非常苛刻，那數組就更適合。 ~~~ >[danger] ##### 對上面的CPU緩存講解（感謝Rain大佬的講解）  >[danger] ##### 鏈表的插入和刪除操作真的就是O(1)么 ~~~ 1.極客時間王爭老師說了刪除在開發實際應用的場景： 1.1.刪除結點中'值等于某個給定值'的結點； 1.2.刪除給定指針指向的結點。 2.針對'第一種情況來分析'，如果給定值，我們想刪除某個元素。那就需要去查到這個元素 鏈表的查詢速度是O(n) 雖然刪除速度是O(1)根據復雜度分析加法法則來說整體的執行速度就是 O(n) 但針對'第二種情況來分析'的話，如果是'單鏈表'你知道指針指向的結點，但是刪除這個結點后， 你還需要將這個被刪除結點的前面結點指針指向，被刪除結點的后面結點，因此你還需要 去查詢被刪除結點的前面結點，你就需要從頭開始查，因此根據復雜度分析O(n), '雙向鏈表'由于知道自己的'前驅結點'因此不用遍歷復雜度O(1) ~~~ >[danger] ##### 時間和空間優化 ~~~ 1.空間換時間的設計思想。當內存空間充足的時候，如果我們更加追求代碼的執行速度， 我們就可以選擇空間復雜度相對較高、但時間復雜度相對很低的算法或者數據結構。 相反，如果內存比較緊缺，比如代碼跑在手機或者單片機上，這個時候，就要反過來 用時間換空間的設計思路。 總結： 對于執行較慢的程序，可以通過消耗更多的內存（空間換時間）來進行優化； 而消耗過多內存的程序，可以通過消耗更多的時間（時間換空間）來降低內存的消耗。 ~~~