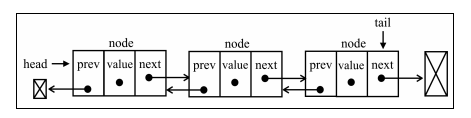
>[success] # 雙向鏈表 ~~~ 1.雙向鏈表相對于單向鏈表來說'鏈接是雙向的：一個鏈向下一個元素， 另一個鏈向前一個元素' 2.就是說雙向鏈表和單鏈表相比不止有'后繼指針next' 它還有一個'前驅指針prev' 3.因為雙向鏈表的結構導致他獨有的特性： 3.1.因為有兩個指針因此它的沒存空間占用會更多，浪費儲存空間 3.2.但可以支持雙向遍歷，這樣也帶來了雙向鏈表操作的靈活性舉個例子： 在單向鏈表中，如果迭代時錯過了要找的元素，就需要回到起點，重新開始迭代。這是雙向 鏈表的一個優勢。 4.好處既可以從頭查找元素也可以從尾部開始查找元素，可以利用長度/2 來決是頭部開始找還是尾部 開始找 ~~~ * 如圖 需要每個結點不只有'后繼指針next' 它還有一個'前驅指針prev'  >[danger] ##### 代碼實現 ~~~ 1.在上面的分析時候，說過鏈表是非連續的空間，我們需要給'每個節點創建對象',并且這個節點存儲的兩個東西 '當前節點的值'，'當前節點對應的下一個節點內存指向'，和'上個結點對應的指向'因此根據這兩點創建一個類 // 保存Node 節點 指針 我們雙向鏈表只要繼承單項鏈表創建的結點類即可 class Node { constructor(element){ this.element = element this.next = undefined } } 2.可以發現雙向鏈表的節點類，構造函數這里我們傳了三個參數，element是必然要有的，剩下兩個 不傳相當于undefined，前后指針指向為undefined // 雙向鏈表 class DoublyNode extends Node { constructor(element, next, prev) { super(element, next); this.prev = prev; } } // 比較元素的公共方法 function defaultEquals(a, b) { return a === b; } ~~~ ~~~ class DoublyNode extends Node { constructor(element, next, prev) { super(element, next); this.prev = prev; } } // 我們的雙向鏈表可以繼承單項鏈表 // 但在這個 基礎上需要稍微的重寫內部一些方法 class DoublyLinkedList extends LinkedList { // {4} constructor(equalsFn = defaultEquals) { super(equalsFn); this.tail = undefined; // 雙向鏈表需要 比單向鏈表多個尾部記錄 } // 添加元素 就需要記錄兩個指針 push(element) { const node = new DoublyNode(element); // 當鏈表沒有元素的時候第一個添加的結點 // 即使尾部也是頭部 if (this.head == null) { this.head = node; this.tail = node; } else { this.tail.next = node; // 之前尾部的結點指向當前結點 node.prev = this.tail; // 現在尾部的頭部指針指向之前尾部 this.tail = node; // 記錄新的尾部結點 } this.count++; } insert(element, index) { if (index >= 0 && index <= this.count) { const node = new DoublyNode(element); let current = this.head; if (index === 0) { // 如果給鏈表首位插入結點 if (this.head == null) { // 當這個這鏈表為空的時候 this.head = node; this.tail = node; } else { // 首位插入不為空的時候 node.next = this.head; this.head.prev = node; this.head = node; } } else if (index === this.count) { // 當往尾部插入的時候 current = this.tail; current.next = node; node.prev = current; this.tail = node; } else { // 往其他位置插入元素的時候 const previous = this.getElementAt(index - 1); current = previous.next; node.next = current; previous.next = node; current.prev = node; node.prev = previous; } this.count++; return true; } return false; } // 刪除 指定角標元素的時候 removeAt(index) { if (index >= 0 && index < this.count) { let current = this.head; if (index === 0) { // 刪除的時候如果是首位 this.head = this.head.next; // 新的頭結點為刪除的頭結點下一結點 if (this.count === 1) { // 如果鏈表中只有一個元素怎尾部結點為undefined this.tail = undefined; } else { // 當前新的頭部結點的前指針就為undefined this.head.prev = undefined; } } else if (index === this.count - 1) { // 尾部結點的時候 current = this.tail; this.tail = current.prev; this.tail.next = undefined; } else { current = this.getElementAt(index); // 找到當前結點 const previous = current.prev; previous.next = current.next; current.next.prev = previous; } this.count--; return current.element; } return undefined; } indexOf(element) { let current = this.head; let index = 0; while (current != null) { if (this.equalsFn(element, current.element)) { return index; } index++; current = current.next; } return -1; } getHead() { return this.head; } getTail() { return this.tail; } clear() { super.clear(); this.tail = undefined; } toString() { if (this.head == null) { return ''; } let objString = `${this.head.element}`; let current = this.head.next; while (current != null) { objString = `${objString},${current.element}`; current = current.next; } return objString; } inverseToString() { if (this.tail == null) { return ''; } let objString = `${this.tail.element}`; let previous = this.tail.prev; while (previous != null) { objString = `${objString},${previous.element}`; previous = previous.prev; } return objString; } } ~~~