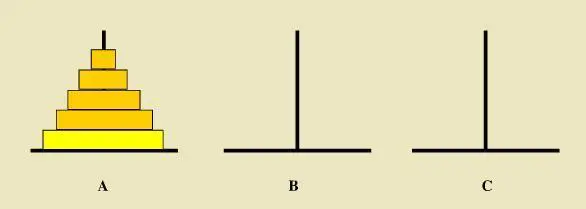
>[success] # 漢諾塔 ~~~ 1.如下圖所示，從左到右有A、B、C三根柱子，其中A柱子上面有從小疊到大的n個圓盤，現要求將A柱子上的圓盤移到 C柱子上去，期間只有一個原則：一次只能移到一個盤子且大盤子不能在小盤子上面，求移動的步驟和移動的次數 ~~~  >[info] ## 棧的思路實現 ~~~~ class Stack { constructor() { this.count = 0; this.items = {}; } push(element) { this.items[this.count] = element; this.count++; } pop() { if (this.isEmpty()) { return undefined; } this.count--; const result = this.items[this.count]; delete this.items[this.count]; return result; } peek() { if (this.isEmpty()) { return undefined; } return this.items[this.count - 1]; } isEmpty() { return this.count === 0; } size() { return this.count; } clear() { /* while (!this.isEmpty()) { this.pop(); } */ this.items = {}; this.count = 0; } toString() { if (this.isEmpty()) { return ''; } let objString = `${this.items[0]}`; for (let i = 1; i < this.count; i++) { objString = `${objString},${this.items[i]}`; } return objString; } } ~~~~ >[danger] ##### 創建一個漢諾塔 ~~~ 1.漢諾塔，是三個柱子為基礎，依次是'初始的源柱子上面依次擺放的要移動的盤子'， '輔助的柱子在將盤子轉移到目標柱子時候輔助用的'，'目標柱子最后盤子要轉移到的柱子' 2.我們將三個柱子看成三個棧，首先要做的就是創建三個柱子，并且個源柱子加上我們要 初始化的盤子 3.關于為什會看成三個棧，首先漢諾塔抽象化，就是一摞東西，無論你怎么操作，只能后進先出， 符合棧的定義，只是變化的是三者每次先后存放位置的順序 ~~~ ~~~ // 漢諾塔 //---------------------------------------------------------------- // 創建一個漢諾塔 // @params plates 盤子個數 function hanoiStack(plates){ // 用三個棧 對象表示漢諾塔的三個柱子 /* 三個柱子依次表示為 source -- 最初始的柱子 dest -- 要移動到的目標柱子 helper -- 用來輔助移動的中間柱子 */ const source = new Stack(); const dest = new Stack(); const helper = new Stack(); // 給 source 初始柱子 添加初始盤子 // 因為盤子是下往上依次是 for(let i=plates;i>0;i--){ source.push(i) } console.log(source) // 后續需要移動盤子的發方法 return towerOfHanoi(plates, source, helper, dest, 'source', 'helper', 'dest'); } ~~~ >[danger] ##### 移動盤子的方法 -- towerOfHanoi * 選自百度百科 ~~~ 1.當盤子的個數為n時，移動的次數應等于2^n – 1（有興趣的可以自己證明試試看）。后來一位美國學者發現一種出人 意料的簡單方法，只要輪流進行兩步操作就可以了。首先把三根柱子按順序排成品字型，把所有的圓盤按從大到小的 順序放在柱子A上，根據圓盤的數量確定柱子的排放順序：若n為偶數，按順時針方向依次擺放 A B C； 若n為奇數，按順時針方向依次擺放 A C B。 ⑴按順時針方向把圓盤1從現在的柱子移動到下一根柱子，即當n為偶數時，若圓盤1在柱子A，則把它移動到B；若圓盤1在柱子B，則把它移動到C；若圓盤1在柱子C，則把它移動到A。 ⑵接著，把另外兩根柱子上可以移動的圓盤移動到新的柱子上。即把非空柱子上的圓盤移動到空柱子上，當兩根柱子都非空時，移動較大的圓盤。這一步沒有明確規定移動哪個圓盤，你可能以為會有多種可能性，其實不然，可實施的行動是唯一的。 ⑶反復進行⑴⑵操作，最后就能按規定完成漢諾塔的移動。 所以結果非常簡單，就是按照移動規則向一個方向移動金片： 如3階漢諾塔的移動：A→C,A→B,C→B,A→C,B→A,B→C,A→C ~~~  ~~~ /* 漢諾塔有三種情況其中兩種是極端情況 1.第一種就是源柱沒有盤子 相當于直接成功 2.第二種就是源柱只有一個盤子，直接移動一次就可以 3.非極端情況就是有一個以上的盤子需要我們平凡操作 */ function towerOfHanoi(plates,source, helper, dest,helperName, sourceName, destName,moves=[]){ // 沒有盤子就一次都不用移動，直接返回空 if(plates === 0) { return moves }else if(plates === 1){ // 直接將第一個移動到第三個 dest.push(source.pop()) const move = {} move[sourceName] = source.toString() move[helperName] = helper.toString() move[destName] = dest.toString() }else{ // 最復雜的多個盤子時候 // 三個柱子 看成動態，不在是固定功能位置 towerOfHanoi(plates - 1, source, dest, helper, sourceName, destName, helperName, moves); dest.push(source.pop()); const move = {}; move[sourceName] = source.toString(); move[helperName] = helper.toString(); move[destName] = dest.toString(); moves.push(move); towerOfHanoi(plates - 1, helper, source, dest, helperName, sourceName, destName, moves); } return moves; } hanoiStack(3) ~~~ * 打印結果  * A→C,A→B,C→B,A→C,B→A,B→C,A→C ~~~ function hanoi(plates, source, helper, dest, moves = []) { if (plates <= 0) { return moves; } if (plates === 1) { moves.push([source, dest]); } else { hanoi(plates - 1, source, dest, helper, moves); moves.push([source, dest]); hanoi(plates - 1, helper, source, dest, moves); } return moves; } console.log(hanoi(3,?'A',?'B',?'C')); ~~~