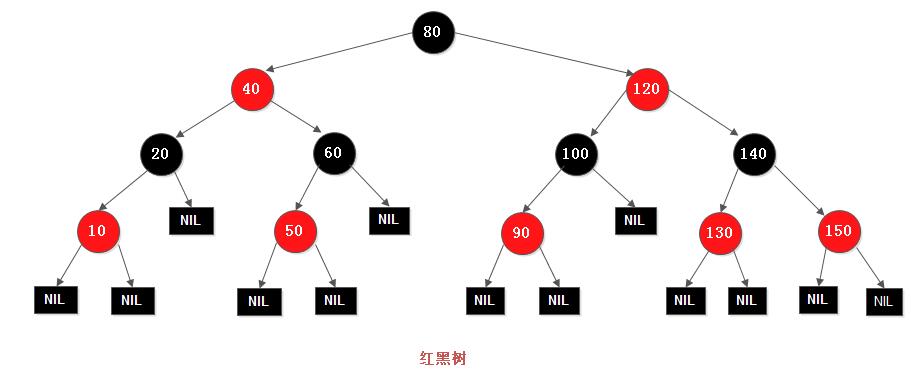
[TOC] ### **什么是紅黑樹** ***** 紅黑樹，一種二叉查找樹，但在每個結點上增加一個存儲位表示結點的顏色，可以是Red或Black。 通過對任何一條從根到葉子的路徑上各個結點著色方式的限制，紅黑樹確保沒有一條路徑會比其他路徑長出倆倍，因而是接近平衡的。 `紅黑樹`，是一棵二叉查找樹，滿足二叉查找樹的一般性質。 ` ` **紅黑樹的5個性質** 1. **每個結點要么是紅的要么是黑的。** ? 2. **根結點是黑的。** ? 3. **每個葉節點(nil節點, 空節點)是黑色的。 注意： 這里的葉子節點是`nil葉子`** ? 4. **每個紅色節點的兩個子節點都是黑色。（從每個葉子到根的所有路徑上不能有兩個連續的紅色節點）** 5. ?**從任一節點到其每個`葉子`的所有路徑都包含相同數目的黑色節點**。 >注意： 性質 3 中指定紅黑樹的每個葉子節點都是空節點，而且并葉子節點都是黑色。但 Java 實現的紅黑樹將使用 null 來代表空節點，因此遍歷紅黑樹時將看不到黑色的葉子節點，反而看到每個葉子節點都是紅色的。 ` ` 性質 4 的意思是：從每個根到節點的路徑上不會有兩個連續的紅色節點，但黑色節點是可以連續的。 因此若給定黑色節點的個數 N，最短路徑的情況是連續的 N 個黑色，樹的高度為 N - 1;最長路徑的情況為節點紅黑相間，樹的高度為 2(N - 1) 。 ` ` 性質 5 是成為紅黑樹最主要的條件，后序的插入、刪除操作都是為了遵守這個規定。 ` `  ### 紅黑樹的應用 紅黑樹的應用比較廣泛，主要是用它來存儲有序的數據，它的時間復雜度是O(lgn)，效率非常之高。 例如，Java集合中的[TreeSet](http://www.cnblogs.com/skywang12345/p/3311268.html)和[TreeMap](http://www.cnblogs.com/skywang12345/p/3310928.html)，C++ STL中的set、map，以及Linux虛擬內存的管理，都是通過紅黑樹去實現的。 ` ` ### 紅黑樹基本操作 #### **紅黑樹的左旋右旋** ***** 紅黑樹的基本操作是**添加**、**刪除**。在對紅黑樹進行添加或刪除之后，都會用到旋轉方法。為什么呢？道理很簡單，添加或刪除紅黑樹中的節點之后，紅黑樹就發生了變化，可能不滿足紅黑樹的5條性質，也就不再是一顆紅黑樹了，而是一顆普通的樹。而通過旋轉，可以使這顆樹重新成為紅黑樹。簡單點說，旋轉的目的是讓樹保持紅黑樹的特性。 旋轉包括兩種：**左旋**和**右旋**。下面分別對它們進行介紹。 ` `  對x進行左旋，意味著"將x變成一個左節點"。 ##### **左旋** 左旋的偽代碼《算法導論》：參考上面的示意圖和下面的偽代碼，理解“紅黑樹T的節點x進行左旋”是如何進行的： ``` LEFT-ROTATE(T, x) y ← right[x] // 前提：這里假設x的右孩子為y。下面開始正式操作 right[x] ← left[y] // 將 “y的左孩子” 設為 “x的右孩子”，即 將β設為x的右孩子 p[left[y]] ← x // 將 “x” 設為 “y的左孩子的父親”，即 將β的父親設為x p[y] ← p[x] // 將 “x的父親” 設為 “y的父親” if p[x] = nil[T] then root[T] ← y // 情況1：如果 “x的父親” 是空節點，則將y設為根節點 else if x = left[p[x]] then left[p[x]] ← y // 情況2：如果 x是它父節點的左孩子，則將y設為“x的父節點的左孩子” else right[p[x]] ← y // 情況3：(x是它父節點的右孩子) 將y設為“x的父節點的右孩子” left[y] ← x // 將 “x” 設為 “y的左孩子” p[x] ← y // 將 “x的父節點” 設為 “y” ``` 理解左旋之后，看看下面一個更鮮明的例子。你可以先不看右邊的結果，自己嘗試一下。  ` ` ##### **右旋**  對x進行左旋，意味著"將x變成一個左節點"。 ` ` 右旋的偽代碼《算法導論》：參考上面的示意圖和下面的偽代碼，理解“紅黑樹T的節點y進行右旋”是如何進行的。 ``` RIGHT-ROTATE(T, y) x ← left[y] // 前提：這里假設y的左孩子為x。下面開始正式操作 left[y] ← right[x] // 將 “x的右孩子” 設為 “y的左孩子”，即 將β設為y的左孩子 p[right[x]] ← y // 將 “y” 設為 “x的右孩子的父親”，即 將β的父親設為y p[x] ← p[y] // 將 “y的父親” 設為 “x的父親” if p[y] = nil[T] then root[T] ← x // 情況1：如果 “y的父親” 是空節點，則將x設為根節點 else if y = right[p[y]] then right[p[y]] ← x // 情況2：如果 y是它父節點的右孩子，則將x設為“y的父節點的左孩子” else left[p[y]] ← x // 情況3：(y是它父節點的左孩子) 將x設為“y的父節點的左孩子” right[x] ← y // 將 “y” 設為 “x的右孩子” p[y] ← x // 將 “y的父節點” 設為 “x” ``` 理解右旋之后，看看下面一個更鮮明的例子。你可以先不看右邊的結果，自己嘗試一下:  **旋轉總結**： (01) 左旋 和 右旋 是相對的兩個概念，原理類似。理解一個也就理解了另一個。 (02) 下面談談如何區分 左旋 和 右旋。 在實際應用中，若沒有徹底理解 左旋 和 右旋，可能會將它們混淆。下面談談我對如何區分 左旋 和 右旋 的理解。 ` ` ##### **區分 左旋 和 右旋** 仔細觀察上面"左旋"和"右旋"的示意圖。我們能清晰的發現，它們是對稱的。無論是左旋還是右旋，被旋轉的樹，在旋轉前是二叉查找樹，并且旋轉之后仍然是一顆二叉查找樹。  **左旋示例圖**(以x為節點進行左旋)： ``` z x / / \ --(左旋)--> x y z / y ``` 對x進行左旋，意味著，將“x的右孩子”設為“x的父親節點”；即，將 x變成了一個左節點(x成了為z的左孩子)！。 因此，**左旋中的“左”，意味著“被旋轉的節點將變成一個左節點”**。 ` ` **右旋示例圖**(以x為節點進行右旋)： ``` y x \ / \ --(右旋)--> x y z \ z ``` 對x進行右旋，意味著，將“x的左孩子”設為“x的父親節點”；即，將 x變成了一個右節點(x成了為y的右孩子)！ 因此，**右旋中的“右”，意味著“被旋轉的節點將變成一個右節點”**。 ` ` #### 紅黑樹基本操作-添加 將一個節點插入到紅黑樹中，需要執行哪些步驟呢？ **第一步: 將紅黑樹當作一顆二叉查找樹，將節點插入。** ``` 紅黑樹本身就是一顆二叉查找樹，將節點插入后，該樹仍然是一顆二叉查找樹。 也就意味著，樹的鍵值仍然是有序的。此外，無論是左旋還是右旋，若旋轉之前這棵樹是二叉查找樹，旋轉之后它一定還是二叉查找樹。 這也就意味著，任何的旋轉和重新著色操作，都不會改變它仍然是一顆二叉查找樹的事實。 ``` **第二步：將插入的節點著色為"紅色"。** ? ? ? ?將插入的節點著色為紅色，不會違背"特性(5)"！少違背一條特性，就意味著我們需要處理的情況越少。接下來，就要努力的讓這棵樹滿足其它性質即可；滿足了的話，它就又是一顆紅黑樹了。 **第三步: 通過一系列的旋轉或著色等操作，使之重新成為一顆紅黑樹。** ``` 第二步中，將插入節點著色為"紅色"之后，不會違背"特性(5)"。那它到底會違背哪些特性呢？ ? ?對于"特性(1)"，顯然不會違背了。因為我們已經將它涂成紅色了。 ? ?對于"特性(2)"，顯然也不會違背。在第一步中，我們是將紅黑樹當作二叉查找樹，然后執行的插入操作。而根據二叉查找數的特點，插入操作不會改變根節點。所以，根節點仍然是黑色。 ? 對于"特性(3)"，顯然不會違背了。這里的葉子節點是指的空葉子節點，插入非空節點并不會對它們造成影響。 ? 對于"特性(4)"，是有可能違背的！ ? ?那接下來，想辦法使之"滿足特性(4)"，就可以將樹重新構造成紅黑樹了。 ``` 添加操作的偽代碼《算法導論》: ``` RB-INSERT(T, z) y ← nil[T] // 新建節點“y”，將y設為空節點。 x ← root[T] // 設“紅黑樹T”的根節點為“x” while x ≠ nil[T] // 找出要插入的節點“z”在二叉樹T中的位置“y” do y ← x if key[z] < key[x] then x ← left[x] else x ← right[x] p[z] ← y // 設置 “z的父親” 為 “y” if y = nil[T] then root[T] ← z // 情況1：若y是空節點，則將z設為根 else if key[z] < key[y] then left[y] ← z // 情況2：若“z所包含的值” < “y所包含的值”，則將z設為“y的左孩子” else right[y] ← z // 情況3：(“z所包含的值” >= “y所包含的值”)將z設為“y的右孩子” left[z] ← nil[T] // z的左孩子設為空 right[z] ← nil[T] // z的右孩子設為空。至此，已經完成將“節點z插入到二叉樹”中了。 color[z] ← RED // 將z著色為“紅色” RB-INSERT-FIXUP(T, z) // 通過RB-INSERT-FIXUP對紅黑樹的節點進行顏色修改以及旋轉，讓樹T仍然是一顆紅黑樹 ``` 結合偽代碼以及為代碼上面的說明，先理解RB-INSERT。理解了RB-INSERT之后，我們接著對 RB-INSERT-FIXUP的偽代碼進行說明。 添加修正操作的偽代碼《算法導論》 ``` RB-INSERT-FIXUP(T, z) while color[p[z]] = RED // 若“當前節點(z)的父節點是紅色”，則進行以下處理。 do if p[z] = left[p[p[z]]] // 若“z的父節點”是“z的祖父節點的左孩子”，則進行以下處理。 then y ← right[p[p[z]]] // 將y設置為“z的叔叔節點(z的祖父節點的右孩子)” if color[y] = RED // Case 1條件：叔叔是紅色 then color[p[z]] ← BLACK ? Case 1 // (01) 將“父節點”設為黑色。 color[y] ← BLACK ? Case 1 // (02) 將“叔叔節點”設為黑色。 color[p[p[z]]] ← RED ? Case 1 // (03) 將“祖父節點”設為“紅色”。 z ← p[p[z]] ? Case 1 // (04) 將“祖父節點”設為“當前節點”(紅色節點) else if z = right[p[z]] // Case 2條件：叔叔是黑色，且當前節點是右孩子 then z ← p[z] ? Case 2 // (01) 將“父節點”作為“新的當前節點”。 LEFT-ROTATE(T, z) ? Case 2 // (02) 以“新的當前節點”為支點進行左旋。 color[p[z]] ← BLACK ? Case 3 // Case 3條件：叔叔是黑色，且當前節點是左孩子。(01) 將“父節點”設為“黑色”。 color[p[p[z]]] ← RED ? Case 3 // (02) 將“祖父節點”設為“紅色”。 RIGHT-ROTATE(T, p[p[z]]) ? Case 3 // (03) 以“祖父節點”為支點進行右旋。 else (same as then clause with "right" and "left" exchanged) // 若“z的父節點”是“z的祖父節點的右孩子”，將上面的操作中“right”和“left”交換位置，然后依次執行。 color[root[T]] ← BLACK ``` ` ` 根據被插入節點的父節點的情況，可以將"當節點z被著色為紅色節點，并插入二叉樹"劃分為**三種情況來處理**。 ① 情況說明：**被插入的節點是根節點**。 ? ? 處理方法：直接把此節點涂為黑色。 ② 情況說明：**被插入的節點的父節點是黑色**。 ? ? 處理方法：什么也不需要做。節點被插入后，仍然是紅黑樹。 ③ 情況說明：**被插入的節點的父節點是紅色**。 ? ? 處理方法：那么，該情況與紅黑樹的“特性(5)”相沖突。這種情況下，被插入節點是一定存在非空祖父節點的；進一步的講，被插入節點也一定存在叔叔節點(即使叔叔節點為空，我們也視之為存在，空節點本身就是黑色節點)。理解這點之后，我們依據"叔叔節點的情況"，將這種情況進一步劃分為3種情況(Case)。  3.1 **被插入的節點的父節點是紅色+叔叔節點也是紅色** * **處理策略** (01) 將“父節點”設為黑色。 (02) 將“叔叔節點”設為黑色。 (03) 將“祖父節點”設為“紅色”。 (04) 將“祖父節點”設為“當前節點”(紅色節點)；即，之后繼續對“當前節點”進行操作。  3.2 **被插入的節點的父節點是紅色,叔叔節點是黑色，且當前節點是其父節點的右孩子** * **處理策略** (01) 將“父節點”作為“新的當前節點”。 (02) 以“新的當前節點”為支點進行左旋。 ` ` 變化前\[當前節點為7節點\]：  變化后：  3.3 **被插入的節點的父節點是紅色,叔叔節點是黑色，且當前節點是其父節點的左孩子** * **處理策略** (01) 將“父節點”設為“黑色”。 (02) 將“祖父節點”設為“紅色”。 (03) 以“祖父節點”為支點進行右旋。 ` ` 變化前\[當前節點為2節點\]：  變化后：  ` ` #### **紅黑樹基本操作-刪除** 將紅黑樹內的某一個節點刪除。需要執行的操作依次是：首先，將紅黑樹當作一顆二叉查找樹，將該節點從二叉查找樹中刪除；然后，通過"旋轉和重新著色"等一系列來修正該樹，使之重新成為一棵紅黑樹。詳細描述如下： **第一步：將紅黑樹當作一顆二叉查找樹，將節點刪除。** ? ? ? ?這和"刪除常規二叉查找樹中刪除節點的方法是一樣的"。分3種情況： ? ? ? ?① 被刪除節點沒有兒子，即為葉節點。那么，直接將該節點刪除就OK了。 ? ? ? ?② 被刪除節點只有一個兒子。那么，直接刪除該節點，并用該節點的唯一子節點頂替它的位置。 ? ? ? ?③ 被刪除節點有兩個兒子。那么，先找出它的后繼節點；然后把“它的后繼節點的內容”復制給“該節點的內容”；之后，刪除“它的后繼節點”。在這里，后繼節點相當于替身，在將后繼節點的內容復制給"被刪除節點"之后，再將后繼節點刪除。這樣就巧妙的將問題轉換為"刪除后繼節點"的情況了，下面就考慮后繼節點。 在"被刪除節點"有兩個非空子節點的情況下，它的后繼節點不可能是雙子非空。既然"的后繼節點"不可能雙子都非空，就意味著"該節點的后繼節點"要么沒有兒子，要么只有一個兒子。若沒有兒子，則按"情況① "進行處理；若只有一個兒子，則按"情況② "進行處理。 **第二步：通過"旋轉和重新著色"等一系列來修正該樹，使之重新成為一棵紅黑樹。** ? ? ? ?因為"第一步"中刪除節點之后，可能會違背紅黑樹的特性。所以需要通過"旋轉和重新著色"來修正該樹，使之重新成為一棵紅黑樹。 ` ` 刪除操作的偽代碼《算法導論》: ``` RB-DELETE(T, z) if left[z] = nil[T] or right[z] = nil[T] then y ← z // 若“z的左孩子” 或 “z的右孩子”為空，則將“z”賦值給 “y”； else y ← TREE-SUCCESSOR(z) // 否則，將“z的后繼節點”賦值給 “y”。 if left[y] ≠ nil[T] then x ← left[y] // 若“y的左孩子” 不為空，則將“y的左孩子” 賦值給 “x”； else x ← right[y] // 否則，“y的右孩子” 賦值給 “x”。 p[x] ← p[y] // 將“y的父節點” 設置為 “x的父節點” if p[y] = nil[T] then root[T] ← x // 情況1：若“y的父節點” 為空，則設置“x” 為 “根節點”。 else if y = left[p[y]] then left[p[y]] ← x // 情況2：若“y是它父節點的左孩子”，則設置“x” 為 “y的父節點的左孩子” else right[p[y]] ← x // 情況3：若“y是它父節點的右孩子”，則設置“x” 為 “y的父節點的右孩子” if y ≠ z then key[z] ← key[y] // 若“y的值” 賦值給 “z”。注意：這里只拷貝z的值給y，而沒有拷貝z的顏色！！！ copy y's satellite data into z if color[y] = BLACK then RB-DELETE-FIXUP(T, x) // 若“y為黑節點”，則調用 return y ``` 結合偽代碼以及為代碼上面的說明，先理解RB-DELETE。理解了RB-DELETE之后，接著對 RB-DELETE-FIXUP的偽代碼進行說明: ``` RB-DELETE-FIXUP(T, x) while x ≠ root[T] and color[x] = BLACK do if x = left[p[x]] then w ← right[p[x]] // 若 “x”是“它父節點的左孩子”，則設置 “w”為“x的叔叔”(即x為它父節點的右孩子) if color[w] = RED // Case 1: x是“黑+黑”節點，x的兄弟節點是紅色。(此時x的父節點和x的兄弟節點的子節點都是黑節點)。 then color[w] ← BLACK ? Case 1 // (01) 將x的兄弟節點設為“黑色”。 color[p[x]] ← RED ? Case 1 // (02) 將x的父節點設為“紅色”。 LEFT-ROTATE(T, p[x]) ? Case 1 // (03) 對x的父節點進行左旋。 w ← right[p[x]] ? Case 1 // (04) 左旋后，重新設置x的兄弟節點。 if color[left[w]] = BLACK and color[right[w]] = BLACK // Case 2: x是“黑+黑”節點，x的兄弟節點是黑色，x的兄弟節點的兩個孩子都是黑色。 then color[w] ← RED ? Case 2 // (01) 將x的兄弟節點設為“紅色”。 x ← p[x] ? Case 2 // (02) 設置“x的父節點”為“新的x節點”。 else if color[right[w]] = BLACK // Case 3: x是“黑+黑”節點，x的兄弟節點是黑色；x的兄弟節點的左孩子是紅色，右孩子是黑色的。 then color[left[w]] ← BLACK ? Case 3 // (01) 將x兄弟節點的左孩子設為“黑色”。 color[w] ← RED ? Case 3 // (02) 將x兄弟節點設為“紅色”。 RIGHT-ROTATE(T, w) ? Case 3 // (03) 對x的兄弟節點進行右旋。 w ← right[p[x]] ? Case 3 // (04) 右旋后，重新設置x的兄弟節點。 color[w] ← color[p[x]] ? Case 4 // Case 4: x是“黑+黑”節點，x的兄弟節點是黑色；x的兄弟節點的右孩子是紅色的。(01) 將x父節點顏色 賦值給 x的兄弟節點。 color[p[x]] ← BLACK ? Case 4 // (02) 將x父節點設為“黑色”。 color[right[w]] ← BLACK ? Case 4 // (03) 將x兄弟節點的右子節設為“黑色”。 LEFT-ROTATE(T, p[x]) ? Case 4 // (04) 對x的父節點進行左旋。 x ← root[T] ? Case 4 // (05) 設置“x”為“根節點”。 else (same as then clause with "right" and "left" exchanged) // 若 “x”是“它父節點的右孩子”，將上面的操作中“right”和“left”交換位置，然后依次執行。 color[x] ← BLACK ``` ` ` ### **紅黑樹相對于哈希表，在選擇使用的時候有什么依據？** ***** 權衡三個因素: 查找速度, **數據量, 內存使用，可擴展性**。 　　總體來說，hash查找速度會比map快，而且查找速度基本和數據量大小無關，屬于常數級別;而map的查找速度是log(n)級別。并不一定常數就比log(n) 小，hash還有hash函數的耗時，明白了吧，如果你考慮效率，特別是在元素達到一定數量級時，考慮考慮hash。但若你對內存使用特別嚴格， 希望程序盡可能少消耗內存，那么一定要小心，hash可能會讓你陷入尷尬，特別是當你的hash對象特別多時，你就更無法控制了，而且 hash的構造速度較慢。 紅黑樹并不適應所有應用樹的領域。如果數據基本上是靜態的，那么讓他們待在他們能夠插入，并且不影響平衡的地方會具有更好的性能。如果數據完全是靜態的，例如，做一個哈希表，性能可能會更好一些。 在實際的系統中，例如，需要使用動態規則的防火墻系統，使用紅黑樹而不是散列表被實踐證明具有更好的伸縮性。Linux內核在管理vm\_area\_struct時就是采用了紅黑樹來維護內存塊的。 紅黑樹通 過擴展節點域可以在不改變時間復雜度的情況下得到結點的秩。 ### **紅黑樹時間復雜度** ***** 紅黑樹雖然本質上是一棵二叉查找樹，但它在二叉查找樹的基礎上增加了著色和相關的性質使得紅黑樹相對平衡，從而保證了**紅黑樹的查找、插入、刪除的時間復雜度最壞為O(log?n)**。