你好，我是你的數據結構課老師蔡元楠，歡迎進入第 04 課時的內容“鏈表在 Apache Kafka 中的應用”。 經過了前三講的學習之后，我相信你已經對數組和鏈表有了比較好的了解了。那在這一講中，我想和你分享一下，數組和鏈表結合起來的數據結構是如何被大量應用在操作系統、計算機網絡，甚至是在 Apache 開源項目中的。 #### 如何重新設計定時器算法 說到定時器（Timer），你應該不會特別陌生。像我們寫程序時使用到的 Java Timer 類，或者是在 Linux 中制定定時任務時所使用的 cron 命令，亦或是在 BSD TCP 網絡協議中檢測網絡數據包是否需要重新發送的算法里，其實都使用了定時器這個概念。那在課程的開頭，我想先問問你，如果讓你來重新設計定時器算法的話，會如何設計呢？ 本質上，定時器的實現是依靠著計算機里的時鐘來完成的。舉個例子，假設時鐘是每秒跳一次，那我們可以根據時鐘的精度構建出 10 秒或者 1 分鐘的定時器，但是如果想要構建 0.5 秒的定時器是無法做到的，因為計算機時鐘最快也只能每一秒跳一次，所以即便當我們設置了 0.5 秒的定時器之后，本質上這個定時器也是只有 1 秒。當然了，在現實中，計算機里時鐘的精度都是毫微秒（Nanosecond）級別的，也就是十億分之一秒。 那回到設計定時器這個算法中，一般我們可以把定時器的概念抽象成 4 個部分，它們分別是： 1. 初始化定時器，規定定時器經過了多少單位時間之后超時，并且在超時之后執行特定的程序； 2. 刪除定時器，終止一個特定的定時器； 3. 定時器超時進程，定時器在超時之后所執行的特定程序； 4. 定時器檢測進程，假設定時器里的時間最小顆粒度為 T 時間，則每經過 T 時間之后都會執行這個進程來查看是否定時器超時，并將其移除。 你可能會問，我們現在只學習了數組和鏈表這兩種數據結構，難道就可以設計一個被如此廣泛應用的定時器算法了嗎？完全沒問題的，那我們就由淺入深，一起來看看各種實現方法優缺點吧。下面的所有算法我們都假設定時器超時時間的最小顆粒度為 T。 * [ ] 維護無序定時器列表 最簡單粗暴的方法，當然就是直接用數組或者鏈表來維護所有的定時器了。從前面的學習中我們可以知道，在數組中插入一個新的元素所需要的時間復雜度是 O(N)，而在鏈表的結尾插入一個新的節點所需要的時間復雜度是 O(1)，所以在這里可以選擇用鏈表來維護定時器列表。假設我們要維護的定時器列表如下圖所示：  它表示現在系統維護了 3 個定時器，分別會在 3T、T 和 2T 時間之后超時。如果現在用戶又插入了一個新定時器，將會在 T 時間后超時，我們會將新的定時器數據結構插入到鏈表結尾，如下圖所示：  每次經過 T 時間之后，定時器檢測進程都會從頭到尾掃描一遍這個鏈表，每掃描到一個節點的時候都會將里面的時間減去 T，然后判斷這個節點的值是否等于 0 了，如果等于 0 了，則表示這個定時器超時，執行定時器超時進程并刪除定時器，如果不等于，則繼續掃描下一個節點。 這種方法的好處是定時器的插入和刪除操作都只需要 O(1) 的時間。但是每次執行定時器檢測進程的時間復雜度為 O(N)。如果定時器的數量還很小時還好，如果當定時器有成百上千個的時候，定時器檢測進程就會成為一個瓶頸了。 * [ ] 維護有序定時器列表 這種方法是上述方法的改良版本。我們可以還是繼續維護一個定時器列表，與第一種方法不一樣的是，每次插入一個新的定時器時，并不是將它插入到鏈表的結尾，而是從頭遍歷一遍鏈表，將定時器的超時時間按從小到大的順序插入到定時器列表中。還有一點不同的是，每次插入新定時器時，并不是保存超時時間，而是根據當前系統時間和超時時間算出一個絕對時間出來。例如，當前的系統時間為 NowTime，超時時間為 2T，那這個絕對時間就為 NowTime + 2T。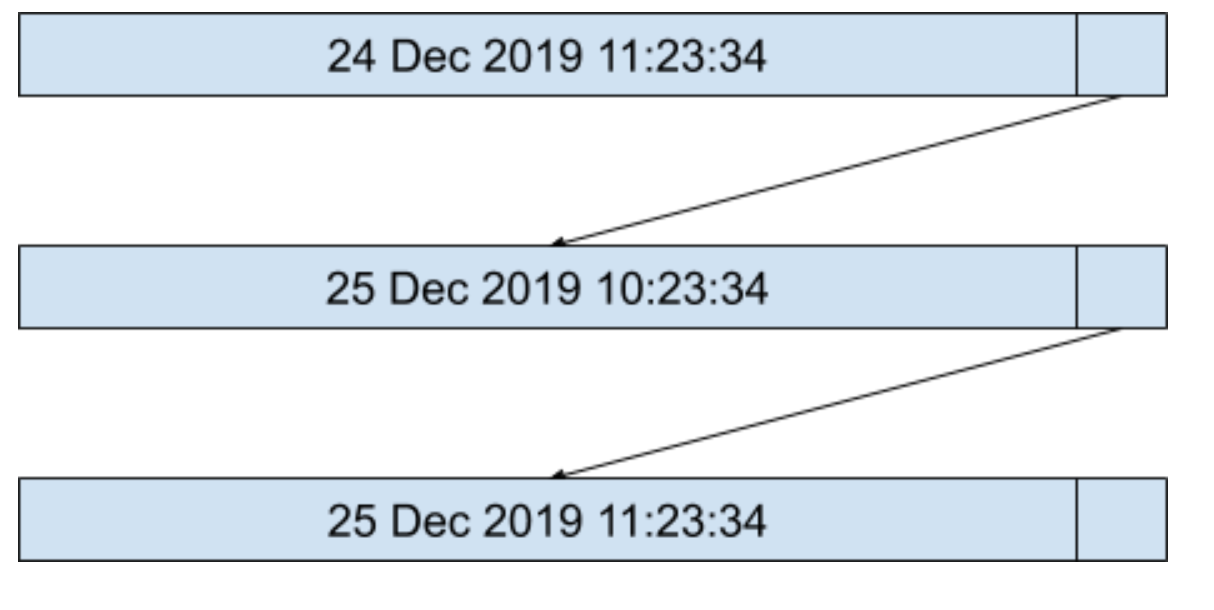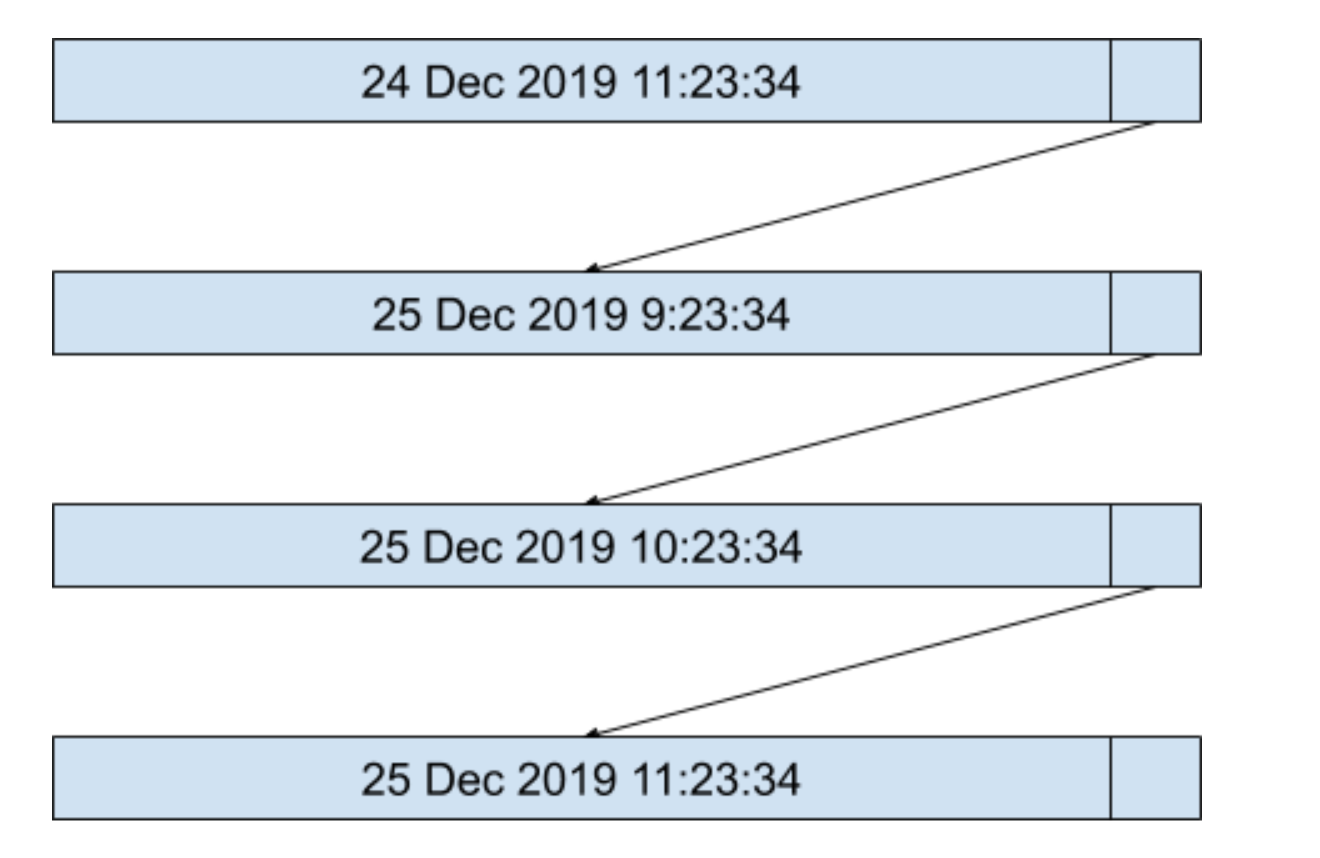 假設原來的有序定時器列表如下圖所示：  當我們要插入一個新的定時器，超時的絕對時間算出為 25 Dec 2019 9:23:34，這時候我們會按照超時時間從小到大的順序，將定時器插入到定時器列表的開頭，如下圖所示：  維護一個有序的定時器列表的好處是，每次執行定時器檢測進程的時間復雜度為 O(1)，因為每次定時器檢測進程只需要判斷當前系統時間是否是在鏈表第一個節點時間之后了，如果是則執行定時器超時進程并刪除定時器，如果不是則結束定時器檢測進程。 這種方法的好處是執行定時器檢測進程和刪除定時器的時間復雜度為 O(1)，但因為要按照時間從小到大排列定時器，每次插入的時候都需要遍歷一次定時器列表，所以插入定時器的時間復雜度為 O(N)。 * [ ] 維護定時器“時間輪” “時間輪”（Timing-wheel ）在概念上是一個用數組并且數組元素為鏈表的數據結構來維護的定時器列表，常常伴隨著溢出列表（Overflow List）來維護那些無法在數組范圍內表達的定時器。“時間輪”有非常多的變種，今天我來解釋一下最基本的“時間輪”實現方式。 首先基本的“時間輪”會將定時器的超時時間劃分到不同的周期（Cycle）中去，數組的大小決定了一個周期的大小。例如，一個“時間輪”數組的大小為 8，那這個“時間輪”周期的大小就為 8T。同時，我們維護一個最基本的“時間輪”還需要維護以下幾個變量： * “時間輪”的周期數，用 S 來表示； * “時間輪”的周期大小，用 N 來表示； * “時間輪”數組現在所指向的索引，用 i 來表示。 現在的時間我們可以用 S×N + i 來表示，每次我們執行完一次定時器檢測進程之后，都會將 i 加 1。當 i 等于 N 的時候，我們將 S 加 1，并且將 i 歸零。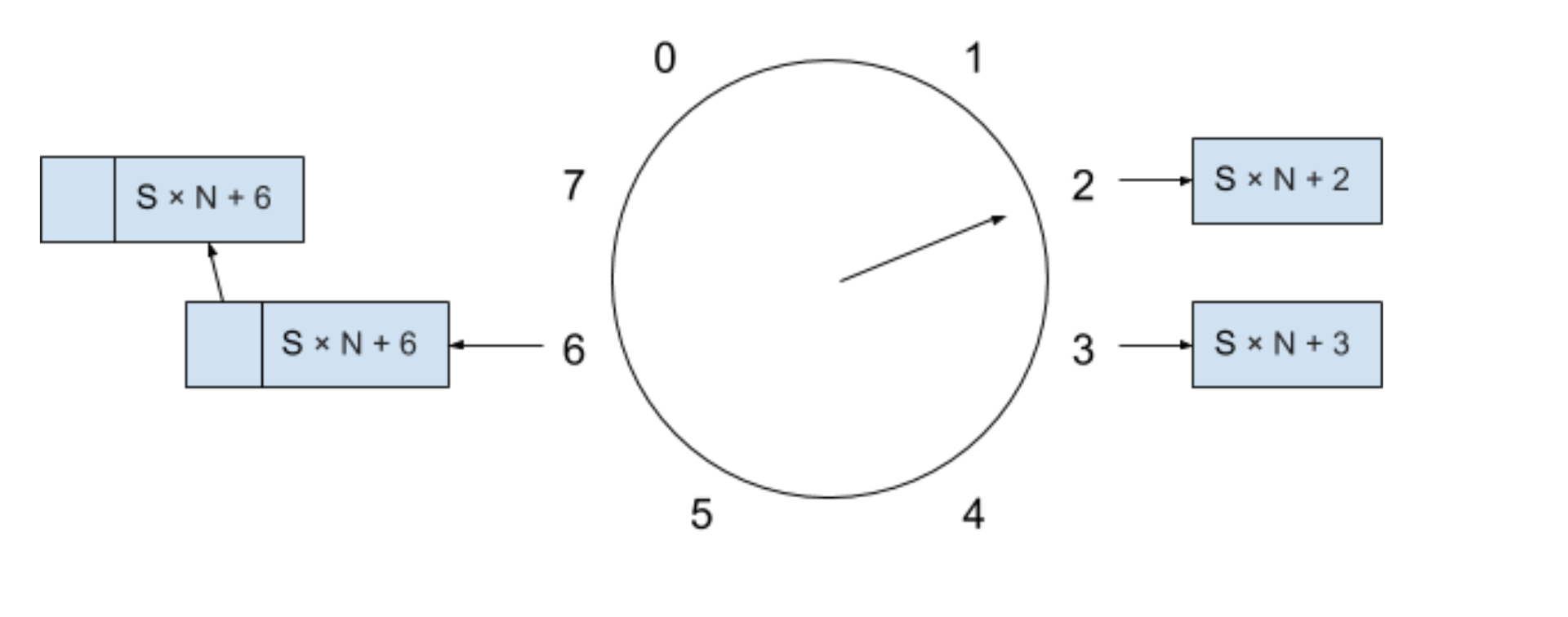因為“時間輪”里面的數組索引會一直在 0 到 N－1 中循環，所以我們可以將數組想象成是一個環，例如一個“時間輪”的周期大小為 8 的數組，可以想象成如下圖所示的環：  那么我們假設現在的時間是 S×N + 2，表示這個“時間輪”的當前周期為 S，數組索引為 2，同時假設這個“時間輪”已經維護了一部分定時器鏈表，如下圖所示：  如果我們想新插入一個超時時間為 T 的新定時器進這個時間輪，因為 T 小于這個“時間輪”周期的大小 8T，所以表示這個定時器可以被插入到當前的“時間輪”中，插入的位置為當前索引為 1 + 2 % 8 = 3 ，插入新定時器后的“時間輪”如下圖所示：  如果我們現在又想新插入一個超時時間為 9T 的新定時器進這個“時間輪”，因為 9T 大于或等于這個“時間輪”周期的大小 8T，所以表示這個定時器暫時無法被插入到當前的周期中，我們必須將這個新的定時器放進溢出列表里。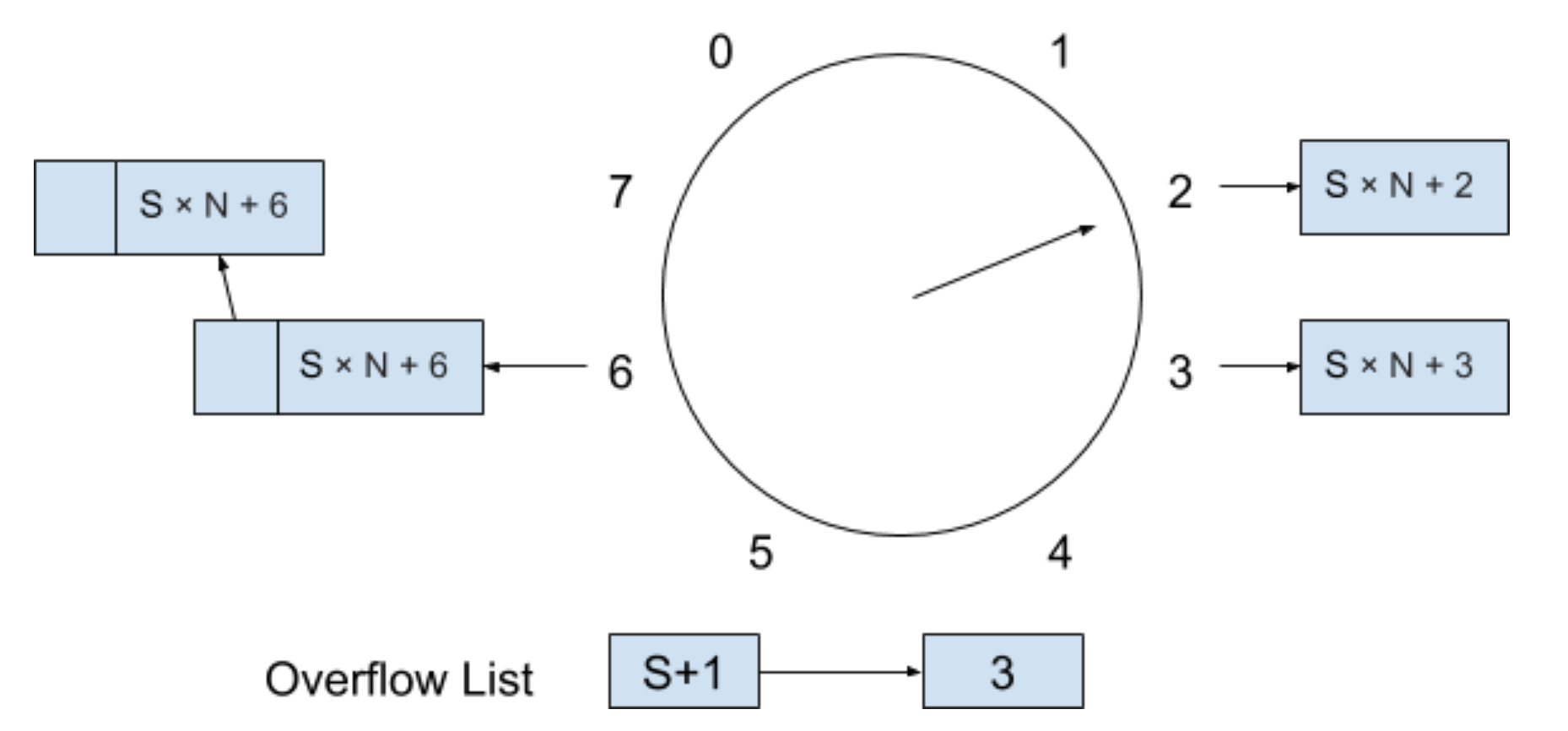溢出列表存放著新定時器還需要等待多少周期才能進入到當前“時間輪”中，我們按照下面公式來計算還需等待的周期和插入的位置： * 還需等待的周期：9T / 8T = 1 * 新定時器插入時的索引位置：(9T + 2T) % 8T = 3 我們算出了等待周期和新插入數組的索引位置之后，就可以更新溢出列表，如下圖所示：  在“時間輪”的算法中，定時器檢測進程只需要判斷“時間輪”數組現在所指向的索引里的鏈表為不為空，如果為空則不執行任何操作，如果不為空則對于這個數組元素鏈表里的所有定時器執行定時器超時進程。而每當“時間輪”的周期數加 1 的時候，系統都會遍歷一遍溢出列表里的定時器是否滿足當前周期數，如果滿足的話，則將這個位置的溢出列表全部移到“時間輪”相對應的索引位置中。 在這種基本“時間輪”的算法里，定時器檢測進程的時間復雜度為 O(1)，而插入新定時器的時間復雜度取決于超時時間，因為插入的新定時器有可能會被放入溢出列表中從而需要遍歷一遍溢出列表以便將新定時器放入到相對應周期的位置。 * [ ] “時間輪”變種算法 基本的“時間輪”插入操作因為維護了一個溢出列表導致定時器的插入操作無法做到 O(1) 的時間復雜度，所以為了 O(1) 時間復雜度的插入操作，一種變種的“時間輪”算法就被提出了。 在這個變種的“時間輪”算法里，我們加了一個 MaxInterval 的限制，這個 MaxInterval 其實也就是我們定義出的“時間輪”數組的大小。假設“時間輪”數組的大小為 N，對于任何需要新加入的定時器，如果超時時間小于 N 的話，則被允許加入到“時間輪”中，否則將不被允許加入。 這種“時間輪”變種算法，執行定時器檢測進程還有插入和刪除定時器的操作時間復雜度都只有 O(1)。 * [ ] 分層“時間輪” 上面所描述到的“時間輪”變種算法，當我們要表達的 MaxInterval 很大而且超時時間顆粒度比較小的時候，會占用比較大的空間。例如，如果時間顆粒度是 1 秒，而 MaxInterval 是 1 天的話，就表示我們需要維護一個大小為 24 × 60 × 60 = 86400 的數組。 那有沒有方法可以將空間利用率提高，而同時保持著執行定時器檢測進程還有插入和刪除定時器的操作時間復雜度都只有 O(1) 呢？答案是使用分層“時間輪”（Hierarchical Timing Wheel）。下面還是以時間顆粒度是 1 秒，而 MaxInterval 是 1 天的例子來說明分層“時間輪”算法。 我們可以使用三個“時間輪”來表示不同顆粒度的時間，分別是小時“時間輪”、分鐘“時間輪”和秒“時間輪”，可以稱小時“時間輪”為分鐘“時間輪”的上一層“時間輪”，秒“時間輪”為分鐘“時間輪”的下一層“時間輪”。分層“時間輪”會維護一個“現在時間”，每層“時間輪”都需要各自維護一個當前索引來表示“現在時間”。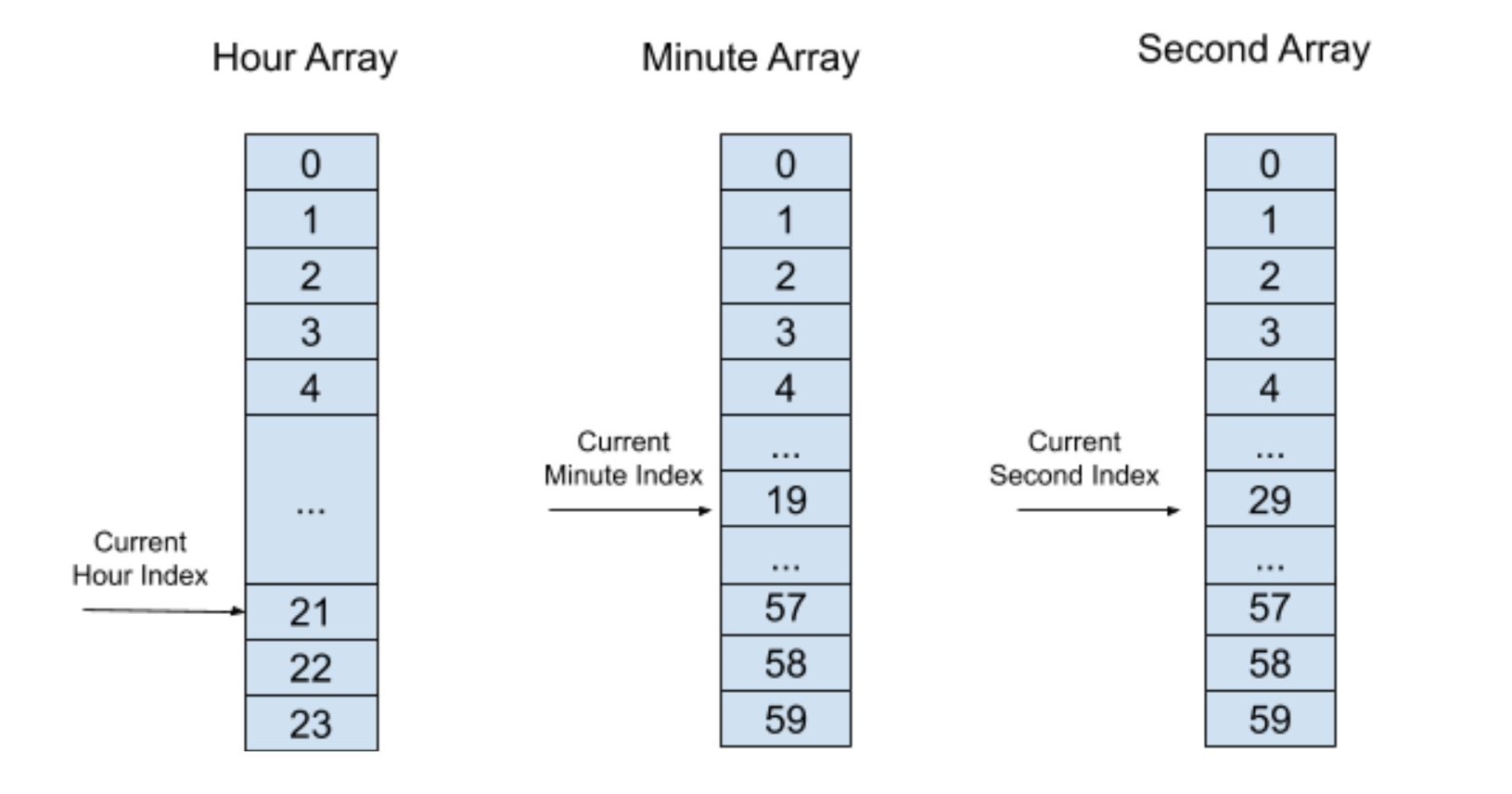例如，分層“時間輪”的“現在時間”是22h:20min:30s，它的結構圖如下圖所示：  當每次有新的定時器需要插入進分層“時間輪”的時候，將根據分層“時間輪”的“現在時間”算出一個超時的絕對時間。例如，分層“時間輪”的“現在時間”是 22h:20min:30s，而當我們要插入的新定時器超時時間為 50 分鐘 10 秒時，這個超時的絕對時間則為 23h:10min:40s。 我們需要先判斷最高層的時間是否一致，如果不一致的話則算出時間差，然后插入定時器到對應層的“時間輪”中，如果一致，則到下一層中的時間中計算，如此類推。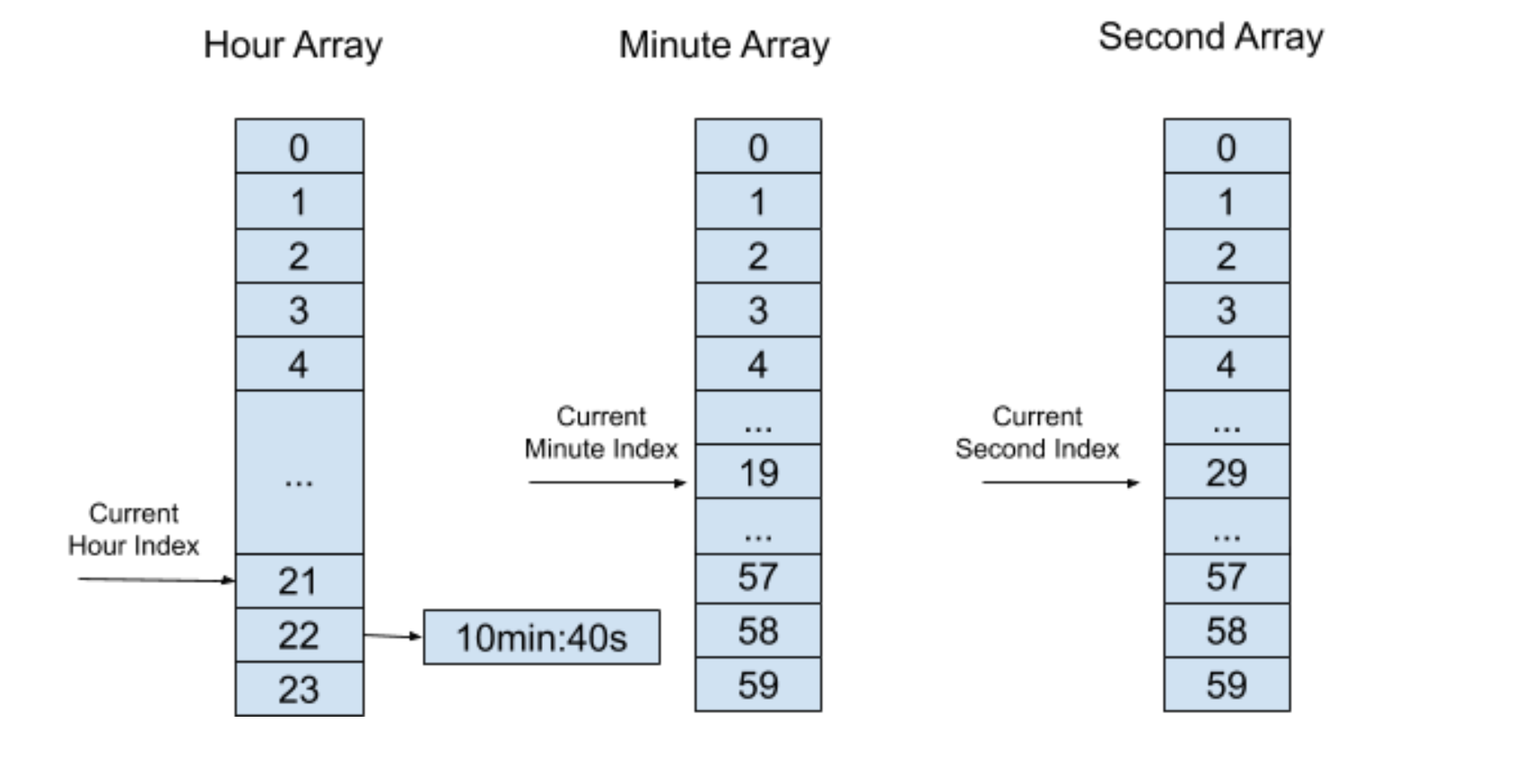在上面的例子中，最高層的時間小時相差了 23－22 = 1 小時，所以需要將定時器插入到小時“時間輪”中的 (1 + 21) % 24 = 22這個索引中，定時器列表里還需要保存下層“時間輪”所剩余的時間 10min:40s，如下圖所示：  每經過一秒鐘，秒“時間輪”的索引都會加 1，并且執行定時器檢測進程。定時器檢測進程需要判斷當前元素里的定時器列表是否為空，如果為空則不執行任何操作，如果不為空則對于這個數組元素列表里的所有定時器執行定時器超時進程。需要注意的是，定時器檢測進程只會針對最下層的“時間輪”執行。 如果秒“時間輪”的索引到達 60 之后會將其歸零，并將上一層的“時間輪”索引加 1，同時判斷上一層的“時間輪”索引里的列表是否為空，如果不為空，則按照之前描述的算法將定時器加入到下一層“時間輪”中去，如此類推。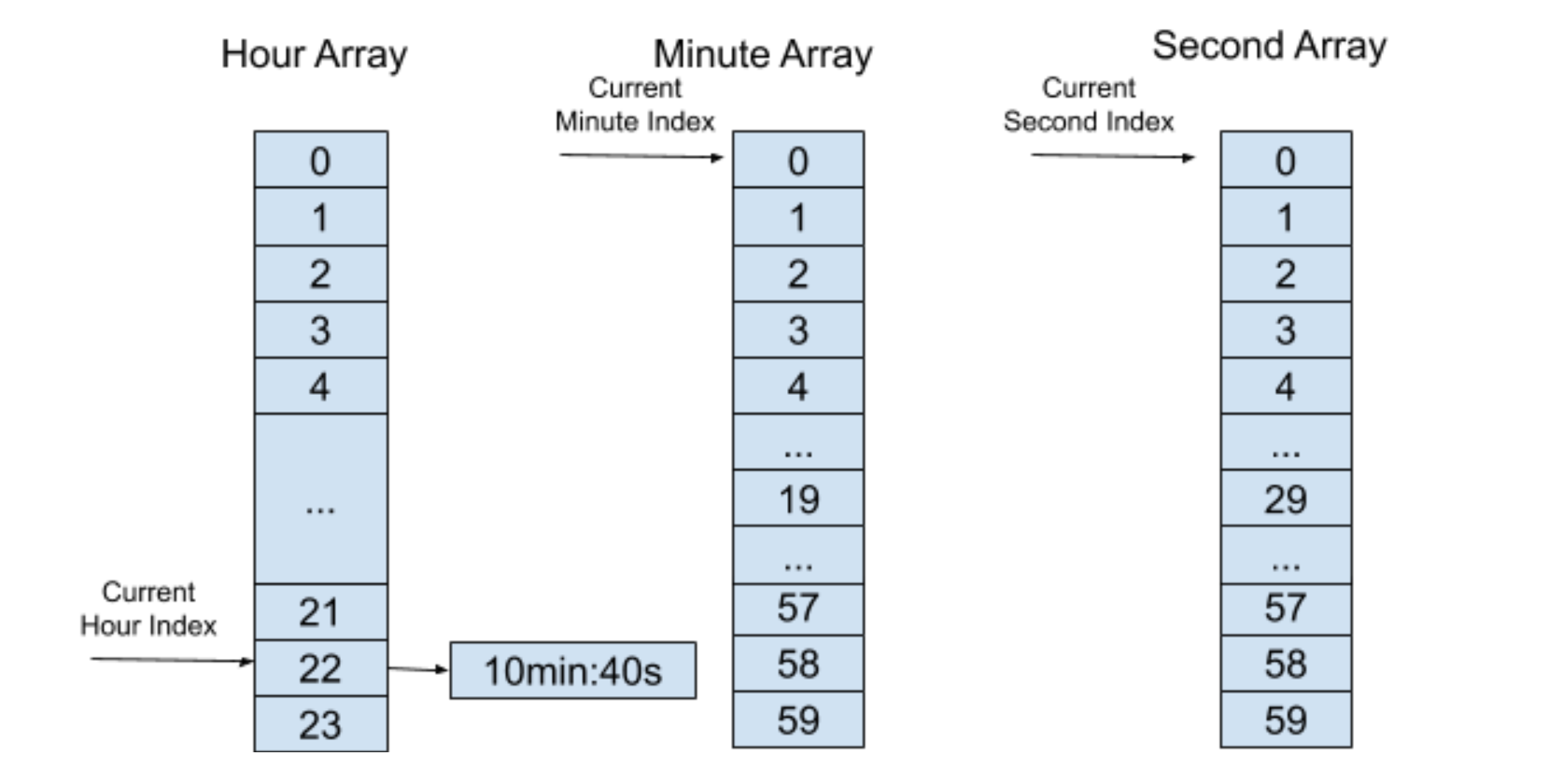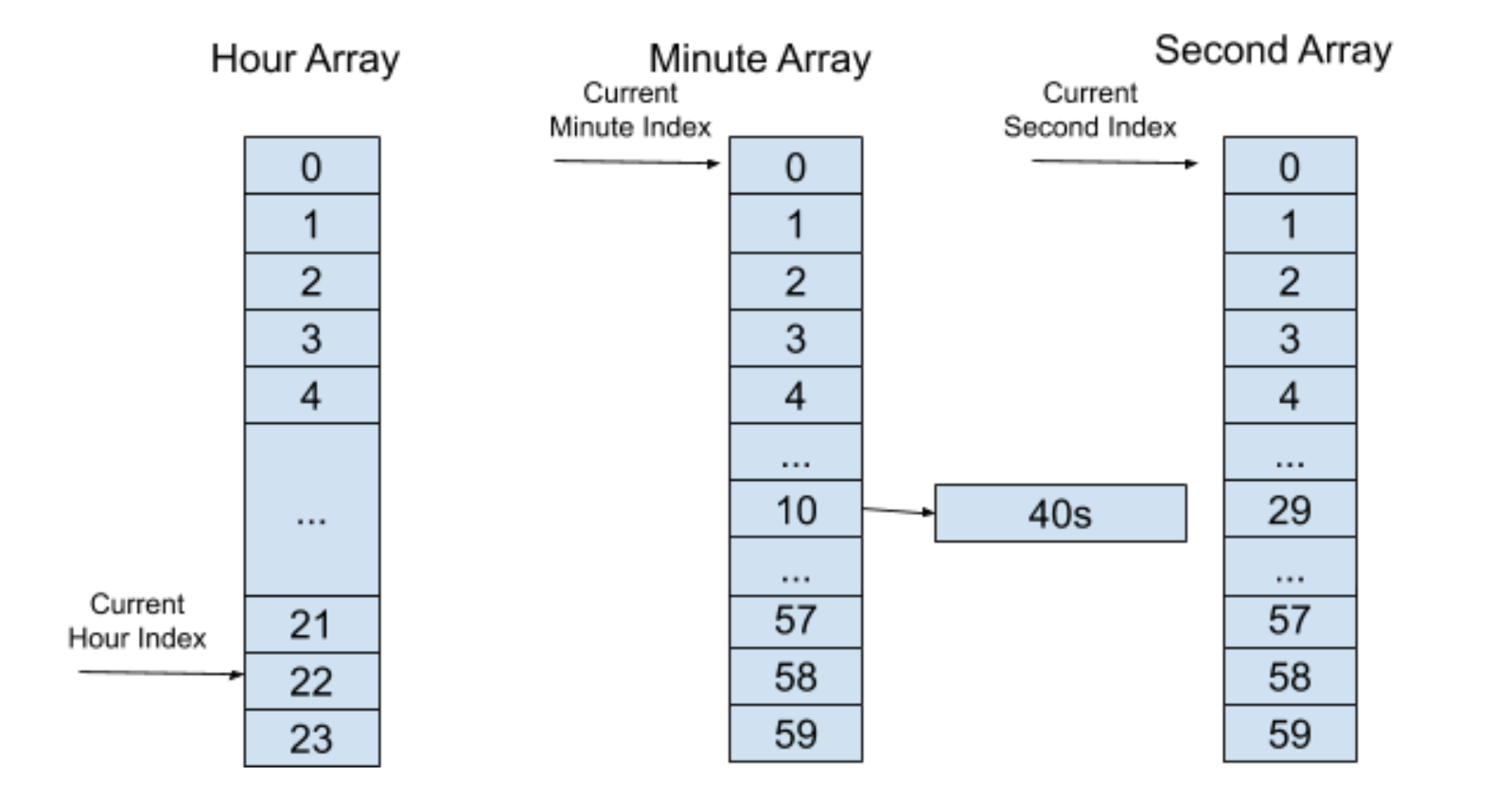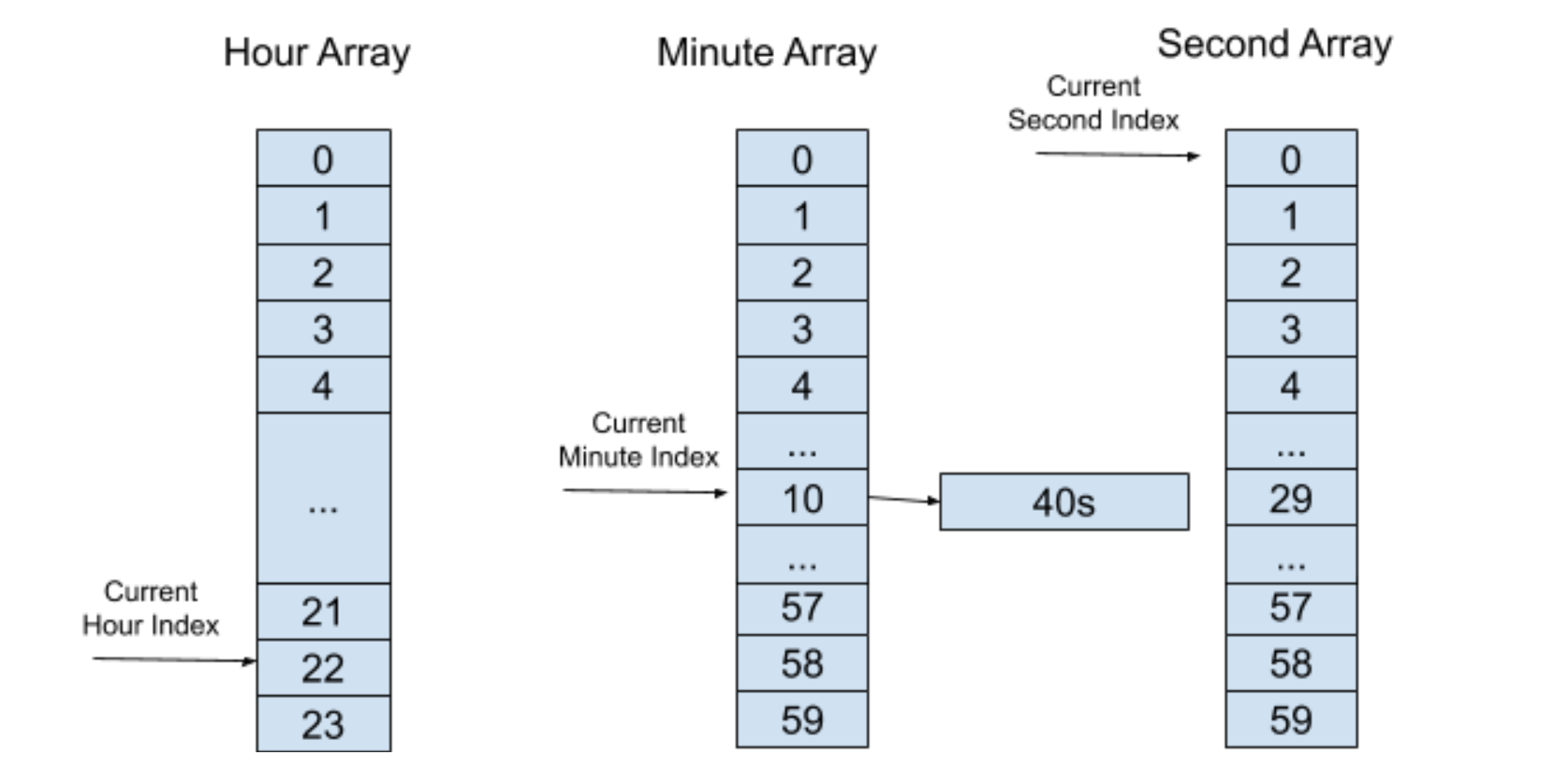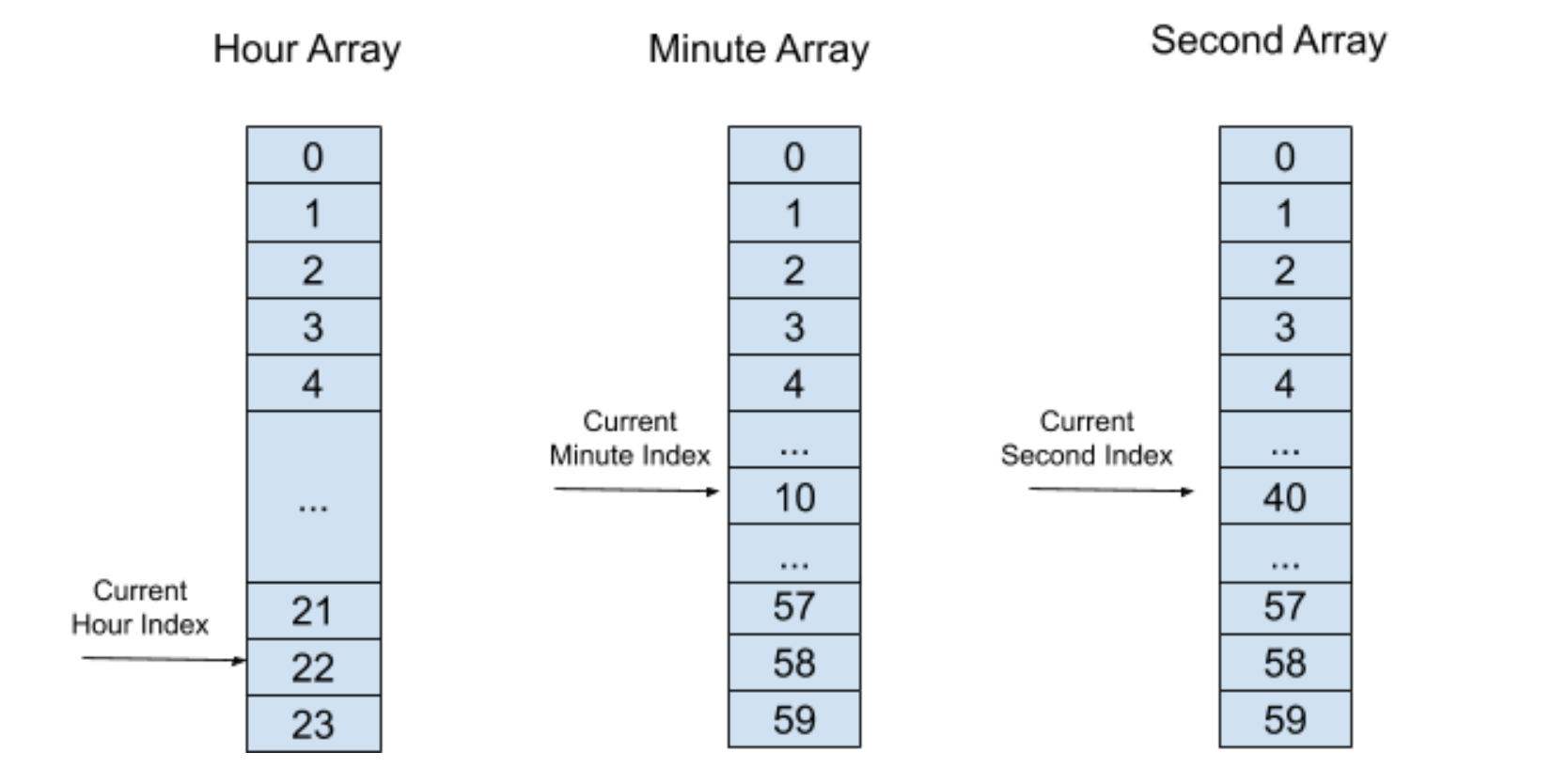 在經過一段時間之后，上面的分層“時間輪”會到達以下的一個狀態：  這時候上層“時間輪”索引里的列表不為空，將這個定時器加入的索引為 10 的分鐘“時間輪”中，并且保存下層“時間輪”所剩余的時間 40s，如下圖所示：  如此類推，在經過 10 分鐘之后，分層“時間輪”會到達以下的一個狀態：  同樣的，我們將這個定時器插入到秒“時間輪”中，如下圖所示：  這個時候，再經過 40 秒，秒“時間輪”的索引將會指向一個元素，里面有著非空的定時器列表，然后執行定時器超時進程并將定時器列表里所有的定時器刪除。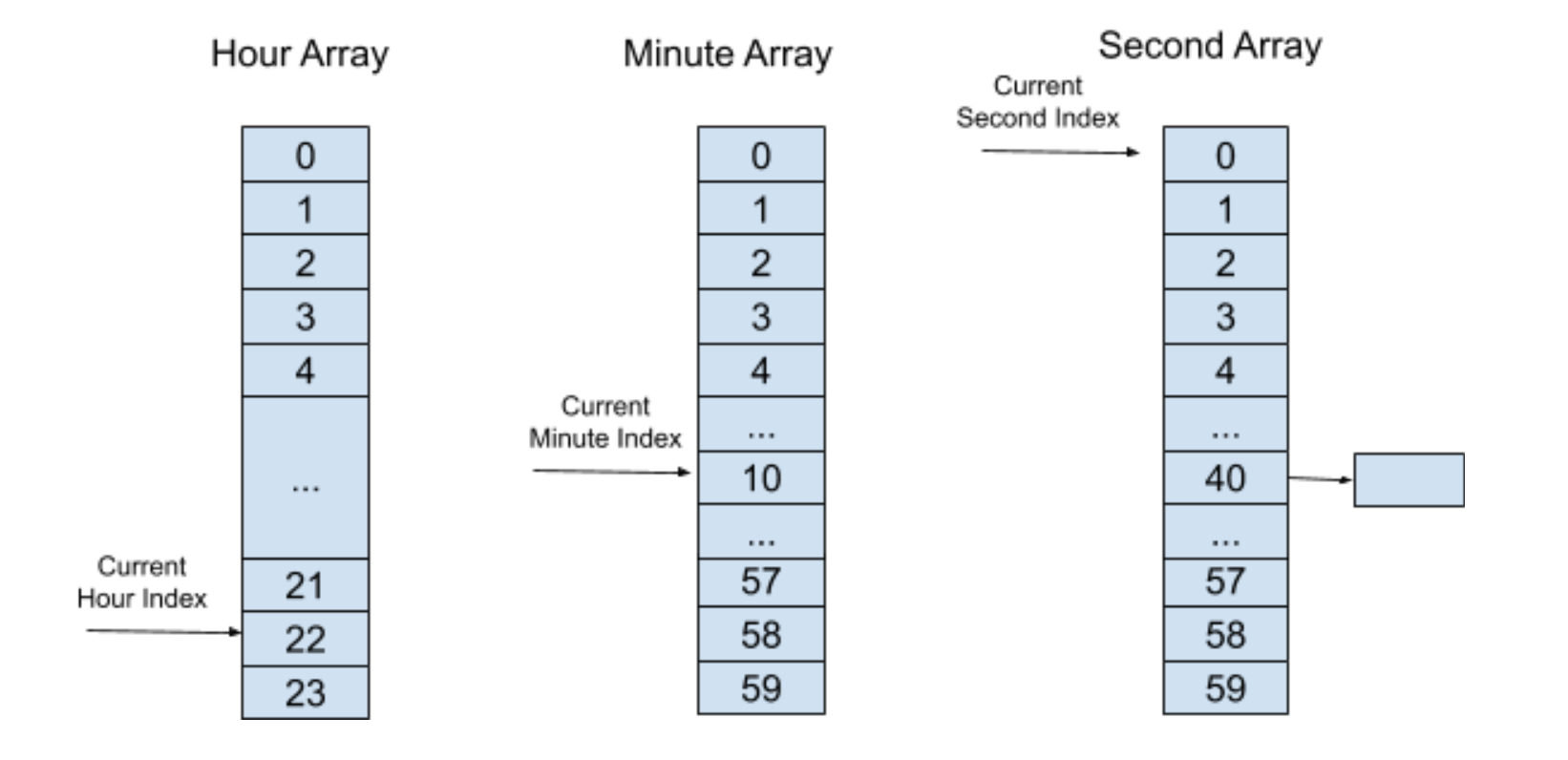  我們可以看到，采用了分層“時間輪”算法之后，我們只需要維護一個大小為 24 + 60 + 60 = 144 的數組，而同時保持著執行定時器檢測進程還有插入和刪除定時器的操作時間復雜度都只有 O(1)。 * [ ] Apache Kafka 的 Purgatory 組件 Apache Kafka 是一個開源的消息系統項目，主要用于提供一個實時處理消息事件的服務。與計算機網絡里面的 TCP 協議需要用到大量定時器來判斷是否需要重新發送丟失的網絡包一樣，在 Kafka 里面，因為它所提供的服務需要判斷所發送出去的消息事件是否被訂閱消息的用戶接收到，Kafka 也需要用到大量的定時器來判斷發出的消息是否超時然后重發消息。 而這個任務就落在了 Purgatory 組件上。在舊版本的 Purgatory 組件里，維護定時器的任務采用的是 Java 的 DelayQueue 類來實現的。DelayQueue 本質上是一個堆（Heap）數據結構，這個概念將會在第 09 講中詳細介紹。現在我們可以把這種實現方式看作是維護有序定時器列表的一種變種。這種操作的一個缺點是當有大量頻繁的插入操作時，系統的性能將會降低。 因為 Kafka 中所有的最大消息超時時間都已經被寫在了配置文件里，也就是說我們可以提前知道一個定時器的 MaxInterval，所以新版本的 Purgatory 組件則采用的了我們上面所提到的變種“時間輪”算法，將插入定時器的操作性能大大提升。根據 Kafka 所提供的檢測結果，采用 DelayQueue 時所能處理的最大吞吐率為 25000 RPS，采用了變種“時間輪”算法之后，最大吞吐率則達到了 105000 RPS。 OK，這節課就講到這里啦，下一課時我將分享“哈希函數的本質及生成方式”，記得按時來聽課哈。