通過前兩講的學習，相信你已經清楚地理解了哈希函數的概念以及它的應用了，那么這一講我們一起學習一下，通過哈希函數產生了哈希碰撞，應該如何處理？在學習完哈希碰撞的解決方式之后，我們就可以完整地認識哈希表這種數據結構了。最后，我會帶你來了解一個哈希表的常用高級應用——BloomFilter。 #### 哈希碰撞的情況 先來看看哈希表的定義，在概念上哈希表可以定義為是一個根據鍵（Key）而直接訪問在內存中存儲位置的值（Value）的數據結構。這里所說的鍵就是指哈希函數的輸入，而這里的值并不是指哈希值，而是指我們想要保存的值。 在現實中， 想要有一個完美的哈希函數，將輸入值轉換成哈希值而不產生哈希碰撞基本是不可能的，所以哈希表在通過鍵來訪問存儲位置的值的時候，是根據我們處理哈希碰撞來決定它自身操作的。那下面我們就以一個具體例子來說明一下，不同的哈希碰撞其解決方式所帶來的底層存儲鍵值對操作的差異。 我們假設存儲哈希表的底層數據結構是一個大小為?3?的數組，我們還是以保存好友電話號碼為例，這個哈希表的鍵是我們好友的名字，哈希表的值是這個好友的電話號碼。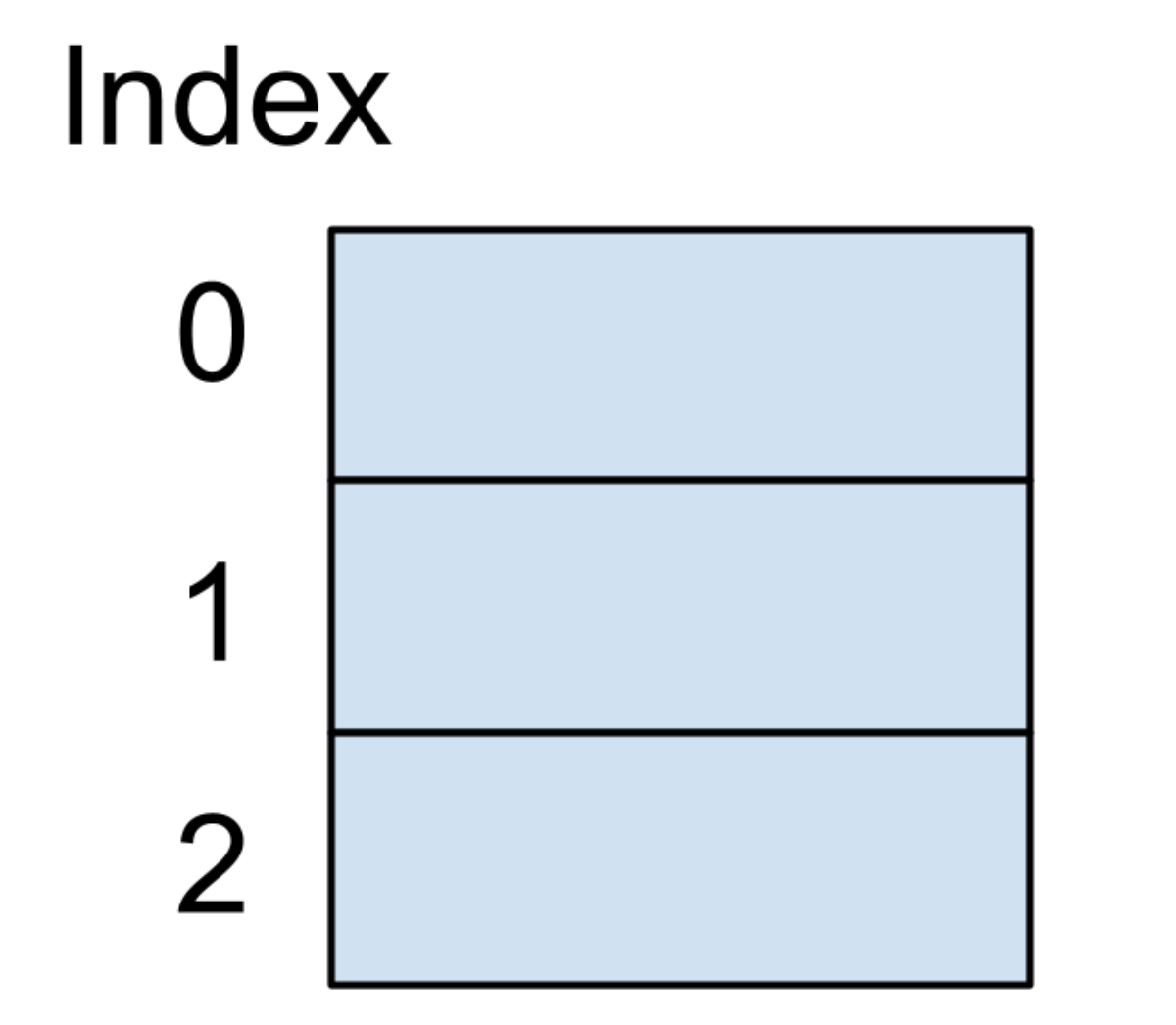剛開始的時候，因為這個數據結構并沒有存儲任何信息，所以數據結構內存結構圖如下圖所示：  假設第一個輸入的鍵值對是（Tom：123456），表示好友的名字叫?Tom，電話號碼為?123456。我們同時假設?Tom?這個字符串在通過哈希函數之后的所產生的哈希值是?0，此時可以把?123456?這個值放在以哈希值為索引的地方，內存結構如下圖所示：  緊接著，我們輸入的第二個鍵值對是（Jack：456789），同時假設?Jack?這個字符串在通過哈希函數之后的所產生的哈希值也是?0，而因為索引為?0?的位置已經存放一個值了，也就表示這時候產生了哈希碰撞。下面我就介紹一下常用的兩種解決哈希碰撞的方式。 * [ ] 開放尋址法（Open Addressing） 開放尋址法本質上是在數組中尋找一個還未被使用的位置，將新的值插入。這樣做的好處是利用數組原本的空間而不用開辟額外的空間來保存值。最簡單明了的方法就是沿著數組索引，往下一個一個地去尋找還未被使用的空間，這種方法叫做線性探測（Linear Probing）。 繼續看剛才的例子，因為索引為?0?的地址已經被使用，那我們就可以尋找下一個位置，也就是索引為?1?的地址，發現還未被使用過，所以我們就可以把?Jack?的電話號碼存放在這里。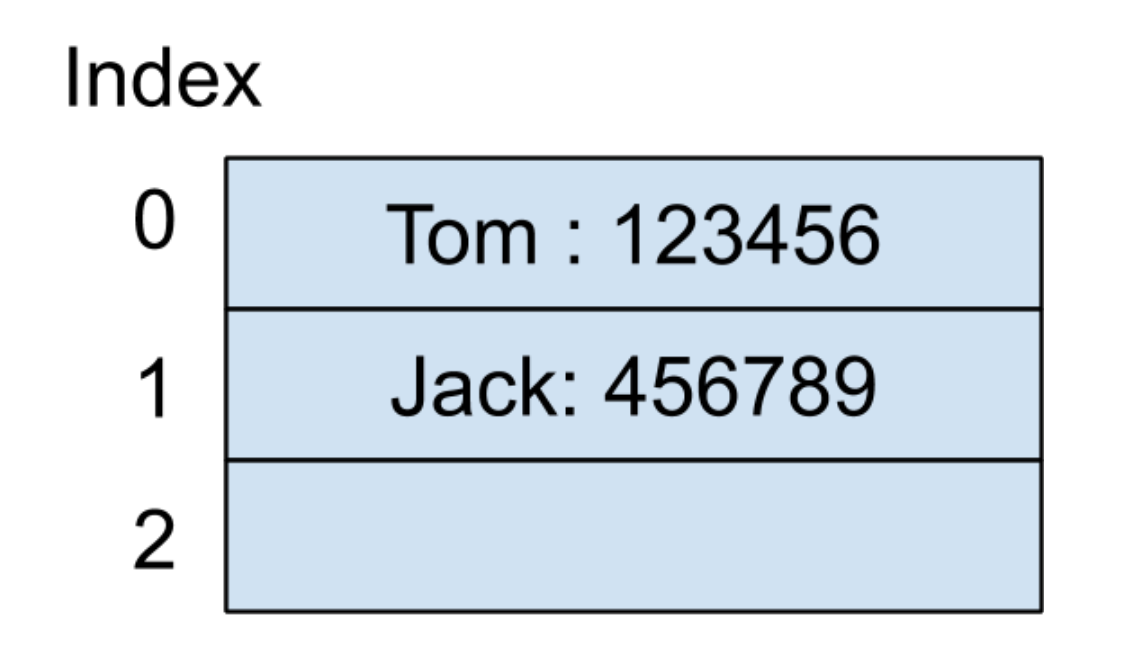因為在產生了哈希碰撞之后，我們無法確定數組里面保存的值到底是哪一個鍵產生的，所以必須將鍵也一并保存在數組中，內存結構如下圖所示：  現在我們繼續輸入第三個鍵值對（Mike：000111）到哈希表中。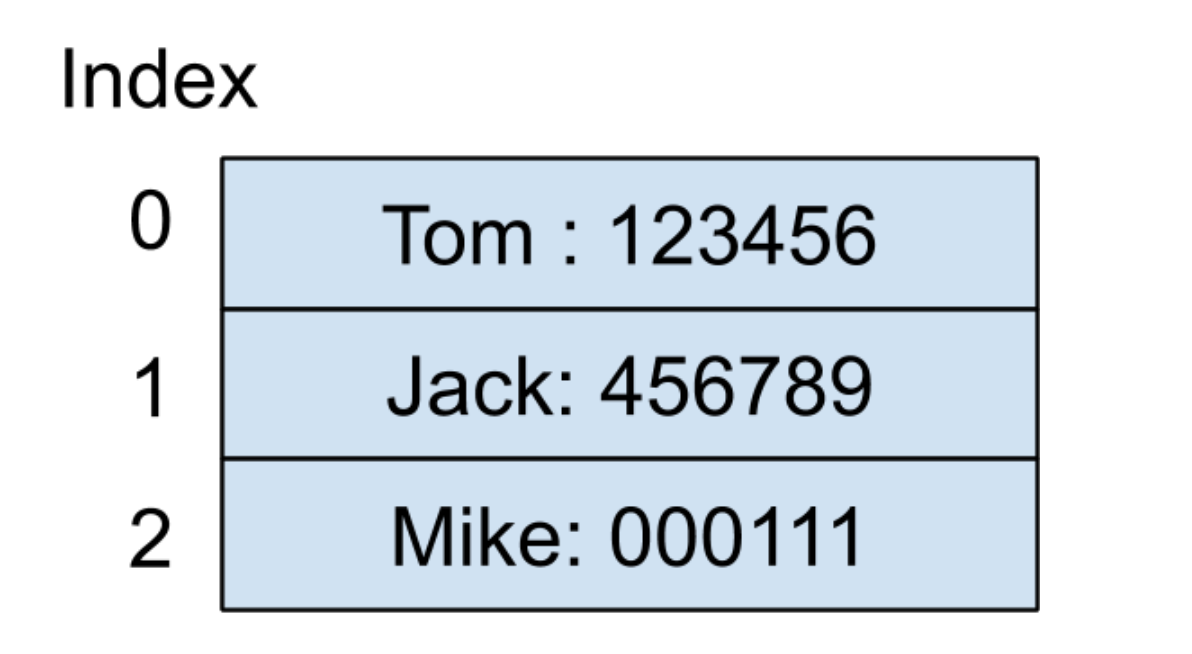假設?Mike?這個輸入通過哈希函數產生的哈希值還是?0，按照線性探測的方法，先來看看下一個索引為?1?的地址，它已經被使用了，所以繼續往下遍歷到索引為?2?的地址，發現還未被使用，此時可以把?Mike?的電話號碼存放在這里，內存結構如下圖所示：  這時候你已經發現了，保存鍵值對的數組已經滿了，如果再有新的元素插入的話，就無法保存新的鍵值對了。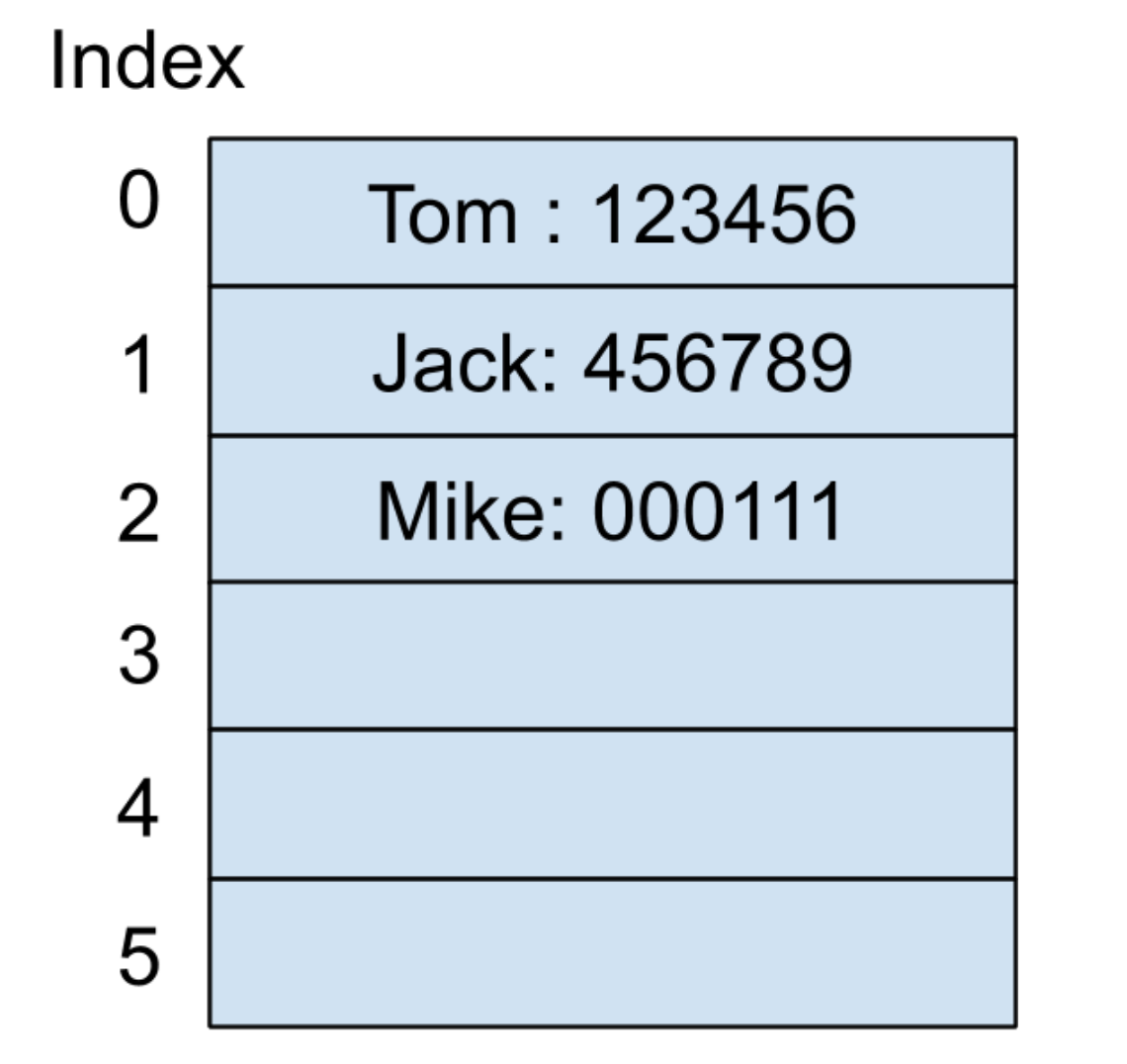一般的做法是將這個數組擴容，比如，再創建一個新的數組，其大小為原來數組大小的兩倍，然后把原來數組的內容復制過去，如果采用這種做法的話，這時的內存結構圖如下所示：  當然了，一般哈希表并不會等到這個數組滿了之后再進行擴容，其實底層數據結構會維護一個叫做負載因子（Load Factor）的數據，負載因子可以被定義為是哈希表中保存的元素個數 / 哈希表中底層數組的大小。當這個負載因子過大時，則表示哈希表底層數組所保存的元素已經很多了，所剩下的未被使用過的數組位置會很少，同時產生哈希碰撞的概率會很高，這并不是我們想看到的。所以一般來說，在負載因子的值超過一定值的時候，底層的數組就得需要進行擴容了，像在?Java?的?JDK?中，都會把負載因子的默認值設為?0.75 （源碼地址）。 采用這種線性探測的好處是算法非常簡單，但它也有自身的缺點。因為每次遇到哈希碰撞的時候都只是往下一個元素地址檢測是否有未被使用的位置存在，所以有可能會導致一種叫做哈希聚集（Primary Clustering）的現象。我們來看看剛剛例子的內存結構圖：  哈希表保存的元素現在都聚集在了?0、1、2?這三個索引位置的地方，如果有新的元素需要插入，而它的哈希值為?1 的話，本來這個位置是不應該產生哈希碰撞的，但由于采用了線性探測的方法，使得這個位置被占用了，所以新插入的元素還得重新再進行一次線性探測。 對此有一些改進的算法被提出用以緩解上面所說的哈希聚集問題，比如平方探測（Quadratic Probing）和二度哈希（Double Hashing）。 * 平方探測指的是每次檢查空閑位置的步數為平方的倍數。例如說，當新元素插入的鍵所產生的哈希值為?i，那下一次的檢測位置為：i?加上?1?的平方、i?減去?1?的平方、i?加上?2?的平方、i?減去?2?的平方、…，以此類推。 * 二度哈希指的是數據結構底層會保存多個哈希函數，當使用第一個哈希函數算出的哈希值產生了哈希碰撞之后，將會使用第二個哈希函數去運算哈希值，…，以此類推。 * [ ] 分離鏈接法（Separate Chaining） 分離鏈接法與鏈表有很大的關系，它的本質是將所有的同一哈希值的鍵值對都保存在一個鏈表中，而哈希表底層的數組元素就是保存這個哈希值對應的鏈表。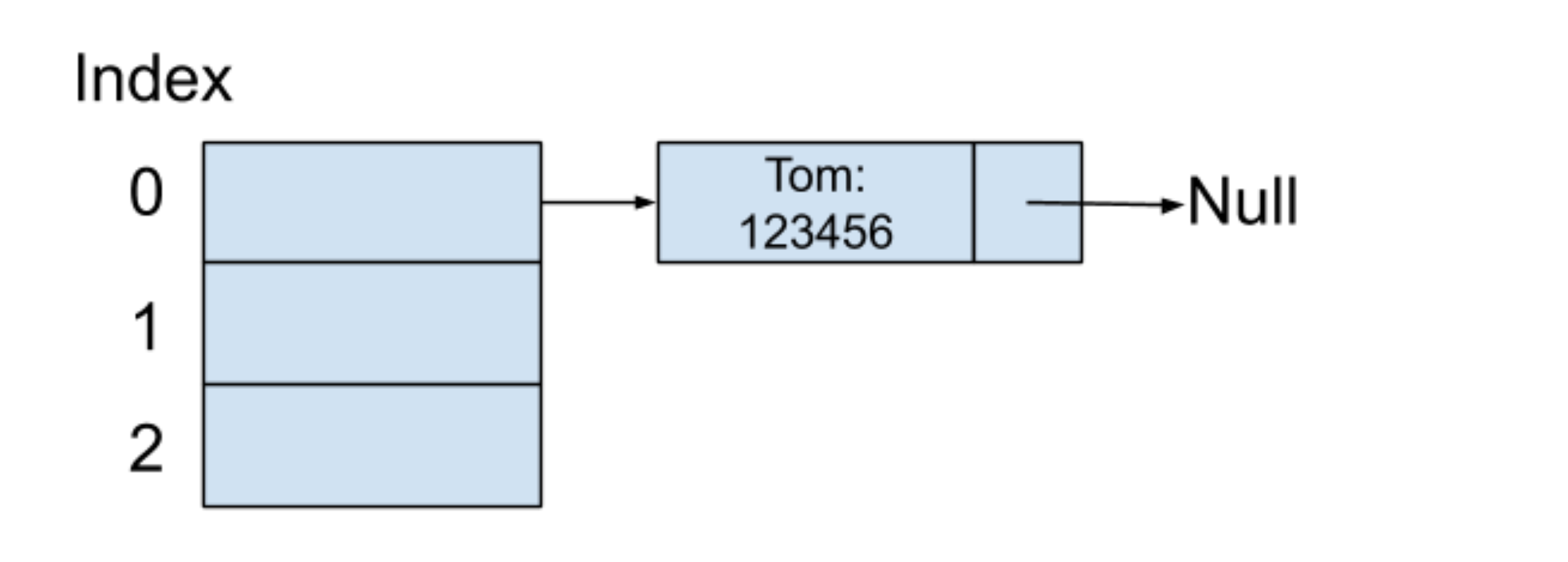 下面我們還是假設存儲哈希表的底層數據結構是一個大小為?3?的數組，還是以保存好友電話號碼為例，剛開始的內存結構圖如下圖所示：  同樣假設第一個輸入的鍵值對是（Tom：123456），表示好友的名字為?Tom，電話號碼為?123456。同時假設?Tom?這個字符串在通過哈希函數之后所產生的哈希值是?0，因為?0?這個索引位置并未使用，所以我們創建一個新的鏈表節點，將鍵值對的值保存在這個新節點中，而?0?這個索引位置的值就是指向新節點的地址，內存結構如下圖所示：  緊接著，我們輸入第二個鍵值對（Jack：456789），同時假設?Jack?這個字符串在通過哈希函數之后所產生的哈希值也是?0，而因為索引為?0?的位置已經存放一個值了，也就表示這時候產生了哈希碰撞。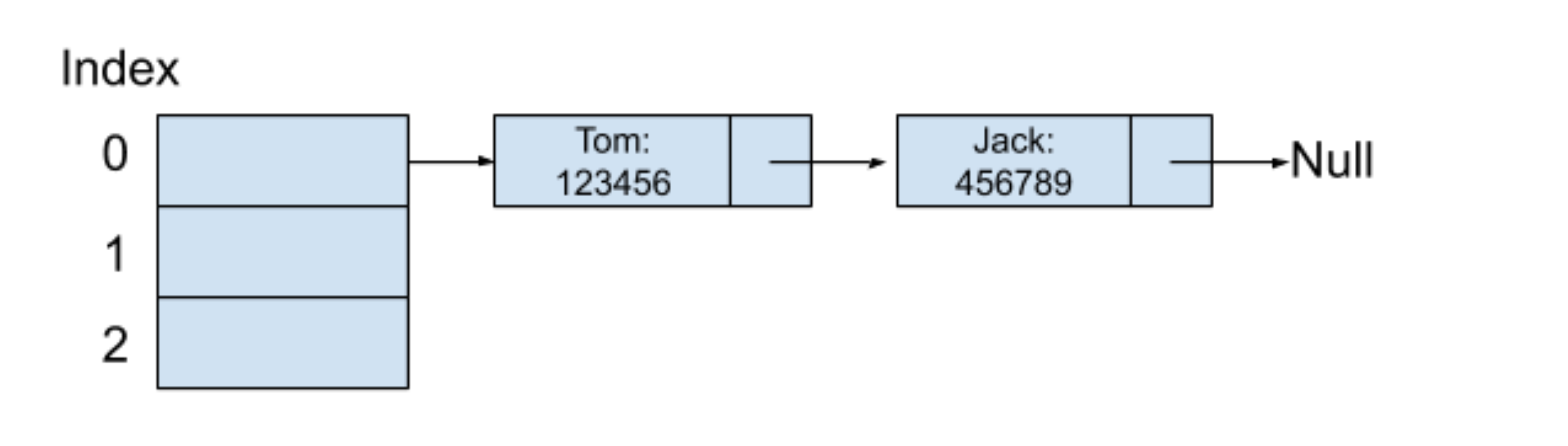但是沒關系，我們只需要再創建一個新的鏈表節點，將這個鍵值對的值保存在新節點中，然后將這新節點插入索引?0?位置鏈表的結尾，內存結構如下圖所示：  采用分離鏈接法會使用到額外的空間來保存新插入的鍵值對。雖然這里舉的例子采用的是鏈表，這在查找一個鍵對應的值時，有可能時間復雜度會降級為?O(N)，但很多時候我們可以進一步將存儲結構優化成紅黑樹，這在樹的章節將會講解到，在?Java JDK?中的?HashMap?類其實就是使用了分離鏈接法。 * [ ] Bloom Filter Bloom Filter?是一個哈希表和位數組相結合的基于概率的數據結構，由?Bloom?在?1970?年提出。它主要用于在超大的數據集合中判斷一個元素是否存在這個集合中，像判斷一個人是否在黑名單中一樣，或者判斷一封郵件是否屬于垃圾郵件的范疇等等。因為使用了位數組，所以使得?Bloom Filter?在空間利用率上非常的高效。而同時它的底層原理和哈希表一致，使得它在查找的時間復雜度上也十分優秀。為什么說它是基于概率的數據結構呢？下面來看看它的原理你就明白了。 Bloom Filter?的原理是將一個元素通過多個哈希函數映射到位數組中。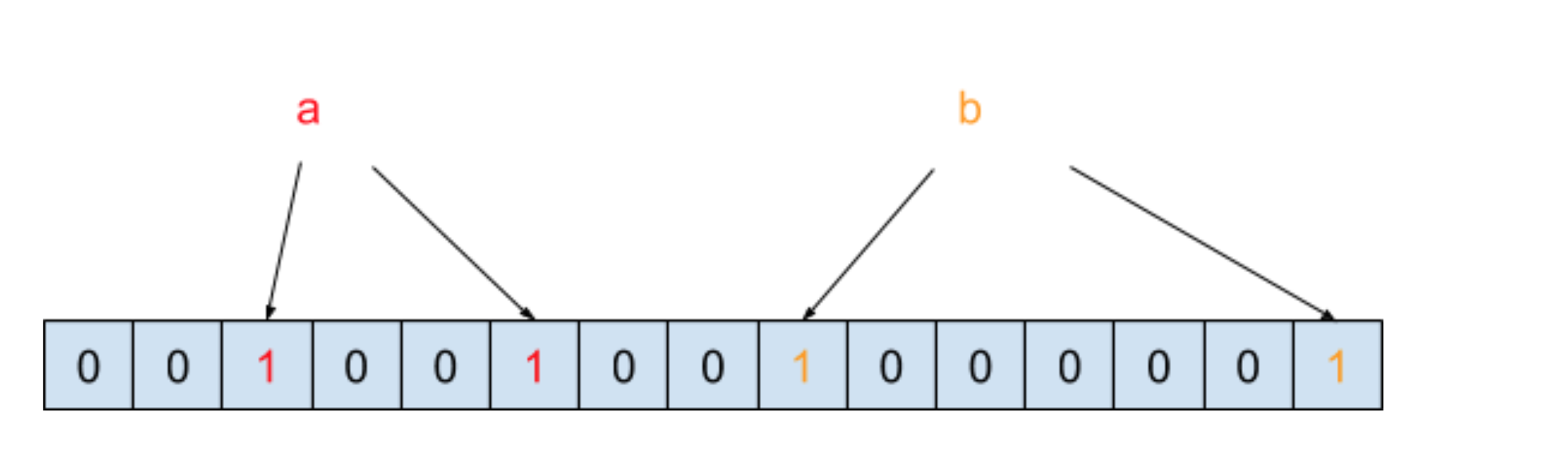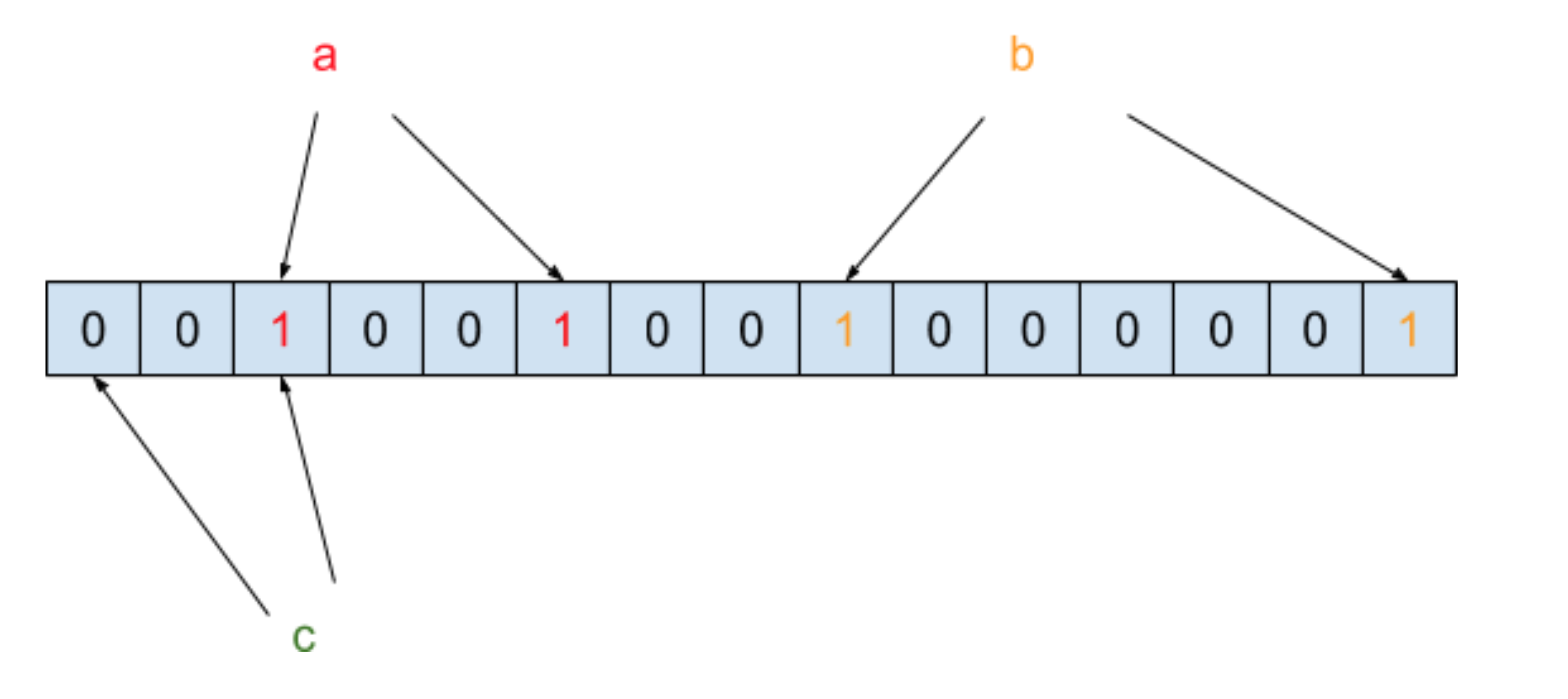我們以黑名單為例來說明，假設哈希函數的個數為?2，也假設黑名單中只有?a?和?b?兩個元素，在通過兩次哈希函數映射到位數組之后，內存結構圖如下圖所示：  我們把元素經過兩次哈希函數之后所對應的哈希值的位置設為?1，此時需要判斷元素?c?是否在黑名單中，需要將?c?也進行兩次哈希函數運算，得到的結果如下圖所示：  你會發現?c?在經過哈希函數映射之后有一個哈希值對應的位置結果為?0，那就表示?c?這個元素一定不在黑名單中。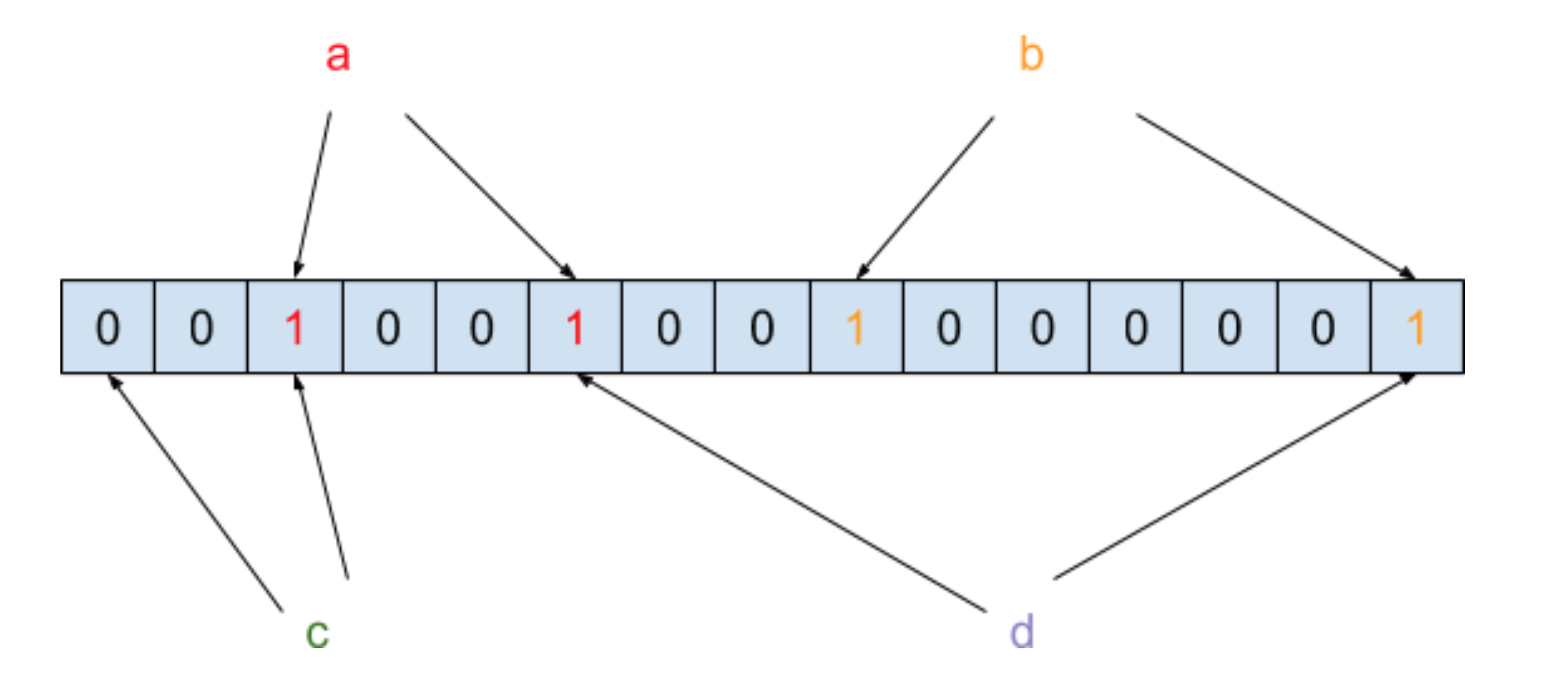此時我們再來還需要判斷元素?d?是否在黑名單中，需要將?d?也進行兩次哈希函數運算，得到的結果如下圖所示：  你會發現?d?在經過哈希函數映射之后有兩個哈希值所對應的位置結果都為?1，但是我們只能判斷?d?這個元素有可能在黑名單中。所以這里存在一個誤判率，也就是說即便經過?N?個哈希函數之后哈希值對應位置的結果都為?1?了，但這個元素不一定真的存在集合中。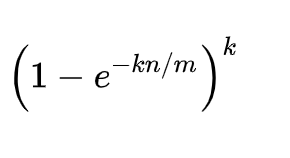 誤判率的公式如下：  其中，m?表示位數組里位的個數，n?表示已經存儲在集合里的元素個數，k?表示哈希函數的個數。