前面的章節我們學習了用樹表達層級化的數據，尤其是應用在數據的檢索方面，樹可以大大的優化數據查詢效率。 而圖相比樹的結構則更為詳盡，圖可以包含一組相互連接的點。在深入圖的規范定義之前，我們先來看看圖有哪些應用場景，為什么需要應用圖這樣的節點間相互連接的數據結構。 #### 圖的應用舉例 社交網絡。社交網絡是典型的網絡結構，圖可以用點來表達社交關系中的人，用點與點之間的連接來表達人與人的關系。比如我們想要去表示誰認識誰、誰和誰溝通、誰能夠影響誰等人與人之間的關系。一個具體的例子是在小紅書上，比如，A 關注了 B 的小紅書，可以用 A 指向 B 的線來連接表示。這些人與人的社交信息，可以用來去解釋社交網絡的信息流動。人與人之間的聯系也定義了我們是誰。 交通網絡。交通網絡也可以用圖來表達。比如所有的城市可以用圖的節點來表示，城市間的交通渠道可以用邊來表示。像最近大家關注的疫情封城措施，也可以用數據結構來理解，就是把交通網絡圖的一些邊進行了阻隔。 互聯網網站連接。我們經常看到網站上會有指向其他網址的超鏈接。如果我們把互聯網所有的網頁定義成圖的節點，那么網頁與網頁之間的邊就是這些鏈接了。如果大家熟悉 Google 經典的網頁排名算法 PageRank，就會知道，搜索引擎正是用指向一個網頁的引用數量去判斷一個網頁的質量。 * [ ] 圖的定義、圖的方向和權重 從數學規范上來講一個圖可以被定義成一個集合 G， G = (V,A) ，其中： * V 是圖的節點集合 * A ? V × V 是節點與節點之間的連接的邊，邊可以是有向或者是無向的 我們來看兩個例子，下圖是一個有向圖的例子，可以看到節點 C 指向節點 A，而節點 A 又指向了節點 D。這個我們可以理解成生活中比如微博上的關注，你可能關注了一個大 V，但是大 V 并不一定關注了你，這就是一個單向的關系，可以用有向圖來建模。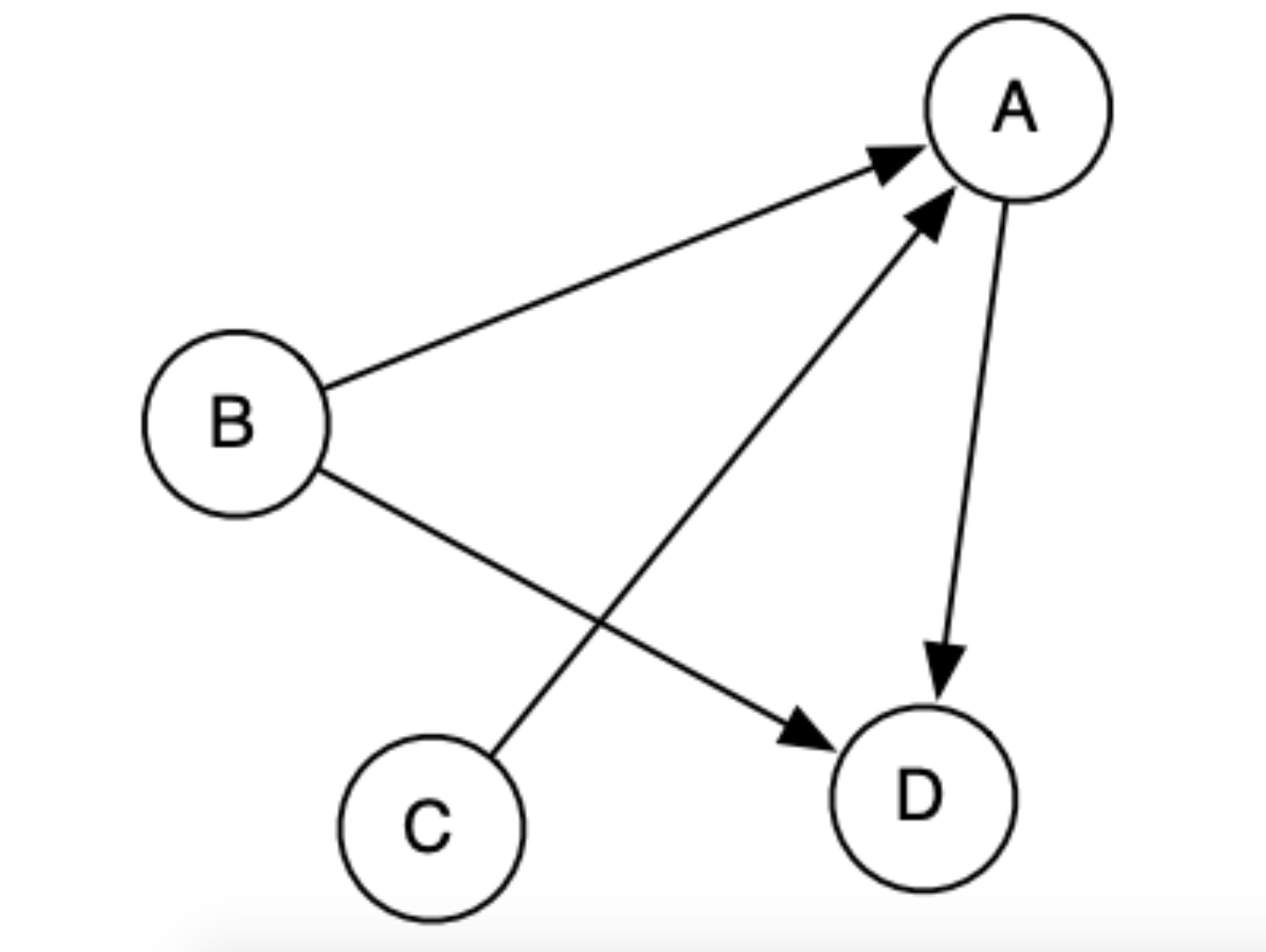  再看下面這個例子，其是一個無向圖的例子。我們可以看到，所有的邊都是沒有方向的，也就是說點和點之間的關系是對稱的。無向圖在生活中也是非常常見的，比如在前面提到的交通網絡，上海如果能通向北京的話，那北京也是能到達上海的。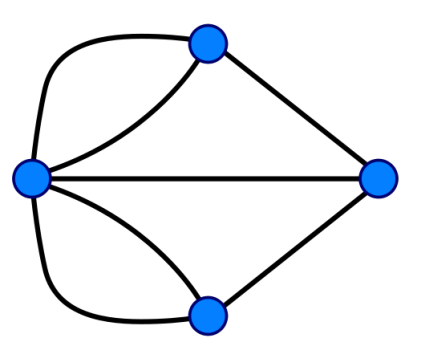  實際上有向圖是比無向圖更常用的圖的類型。因為你可以把無向的邊理解成同時由兩個有向邊組成。事實上我們在實現無向圖的時候也經常用兩條邊來實現。比如說在微博上，如果你關注了 A，并且 A 也關注了你，我們就可以把你和 A 的關系看作是一條無向的邊。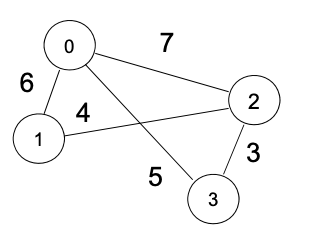 圖的邊也可以有權重。比如下圖這個例子就是一個有權重的圖，你可以看到 0 和 2 的邊有權重 7，而 2 和 3 的邊權重為 3。權重在網絡關系中也很常見。比如在交通網絡中，假設北京去上海的交通費用是 1000 元，而上海去武漢的交通費用是 2000 元；再比如在商品交易網絡中，如果把世界上所有的商品做成一個圖，商品與商品之間的交易價格定義成邊，那么如果要用人民幣購買口罩，則可能是 10 元人民幣，但如果用人民幣兌換成美元，則需要 7 元人民幣。  #### 圖和樹的區別 學習到這里，你可能還會有疑問，樹也是有節點和邊，那么圖和樹究竟有啥區別呢？其實本質區別是，樹和圖所要抽象的數據關系不一樣。樹表達的是層級化的結構，圖是用來表達網絡化的結構。 例如，我們在樹的章節中經常用公司的上下級關系來舉例，因為樹是有父節點和子節點這樣的關系存在的。樹有一個根節點，下面的每一棵子樹都有唯一的根節點；而圖則不一樣，圖的每一個節點都可以看作是平等的，并且節點與節點之間的連接也更為自由。在樹中一個父節點只能與它的子節點相連，但不會看到父節點與孫子節點相連。但是在圖中，任意節點都是可以相連的。 #### 圖的實現和內存表達 相信你學到這里一定迫不及待地想要自己實現圖了。圖有兩種常見的實現方式，一種是鄰接矩陣法，另一種是鄰接鏈表法。 * [ ] 1.?鄰接矩陣法 使用鄰接矩陣法的基本思想是開一個超大的數組，用數組中間元素的 true / false 來表達邊。具體什么意思呢？比如你有 V 個節點的圖，那么就需要一個 V×V 大小的數組。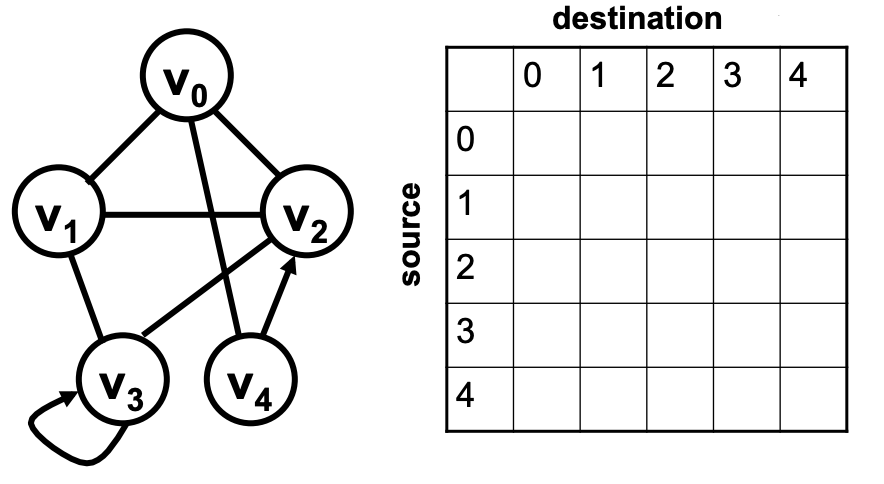 我們來看一個例子，下面這個例子中有 V0 - V4 總共 5 個節點，可以看到我們已經畫出了一個 5 × 5 的二維數組 G。如果學習了之前數組章節中的二維數組，就知道可以用 G[i][j] 這樣的尋址方式來找到第 i 行第 j 列的元素。在這個例子中規定，如果有從 Vi 指向 Vj 的邊，那么 G[i][j] = true，反之如果沒有邊，則 G[i][j] = false。不如一起來看看在這個例子中有哪些數組元素會是 true。 我們首先看看 V4 指向 V2 的邊，即 G[4][2] = true；接著再看看 V0 和 V2 之間的邊是無向的，也就是說，我們需要 G[0][2] = true，同時 G[2][0] = true；最后看到 V3 有指向自己的邊，所以 G[3][3] 也是 true，可以發現鄰接矩陣法的實際上存儲的是所有的邊。  * [ ] 2. 鄰接鏈表法 鄰接鏈表法則是不一樣的思路了，它的核心思想是把每一個節點所指向的點給存儲起來。 比如還是同樣一個圖 V0 - V4，如果我們用鄰接鏈表法表達的話，則需要一個含有 5 個元素的數組，用來存儲這樣 5 個節點；然后每個節點所指向的點都會維護在一個鏈表中。比如在這個例子中，V0 指向了 V1、V4、V2 三個節點，那么在內存中就會有從 0 指向 1 接著指向 2、4 類似這樣的一個鏈表。同理我們看 V4 指向了 V0 和 V2，則在內存中就要維護一個 4→0→2 的單向鏈表。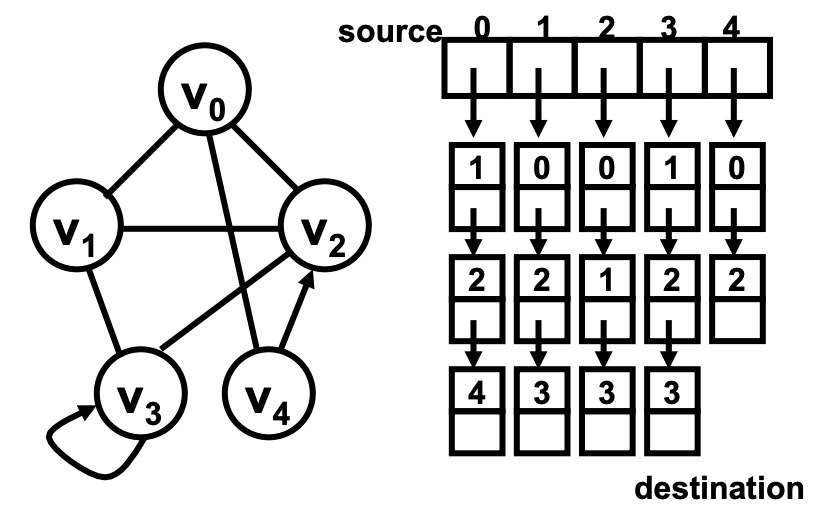  這兩種實現方式有什么區別呢？鄰接矩陣法因為存儲在二維數組中，我們在之前的章節中已經掌握了數組的特點，那就是隨機訪問快。在這里也一樣，鄰接矩陣法可以更快地添加和刪除邊，也可以更快地判斷邊是否存在，你只需要對 G[i][j] 這個元素操作就行了。 但是鄰接矩陣法需要一個 O(V^2) 的內存空間，相對來說更適合邊比較多的圖，這樣就可以更好的利用這些內存。因為鄰接矩陣法存儲的是邊，不管有多少邊，它都需要一樣的內存。 鄰接鏈表法可以更快地操作一個節點相鄰的節點，在一個稀疏的圖中也就是邊比較少的圖中，鄰接鏈表法的效率其實是比較高的。因為每一個單鏈表都比較短，我們知道修改鏈表的時間復雜度是 O(n)，同樣也適用于鄰接鏈表法。如果鄰接鏈表法的邊比較多，則鏈表就會比較長，進而影響我們的操作效率。鄰接鏈表法的空間復雜度需要 O(|V| + |E|) ?的內存空間。 #### 總結 這一講我們學習了圖的基本概念，搞清楚了圖和樹的區別，之后又仔細探究了圖的兩種實現方法。這些都為我們應用圖這個數據結構打下了良好的基礎，后面我們會馬上學習圖在現實工業界的應用。