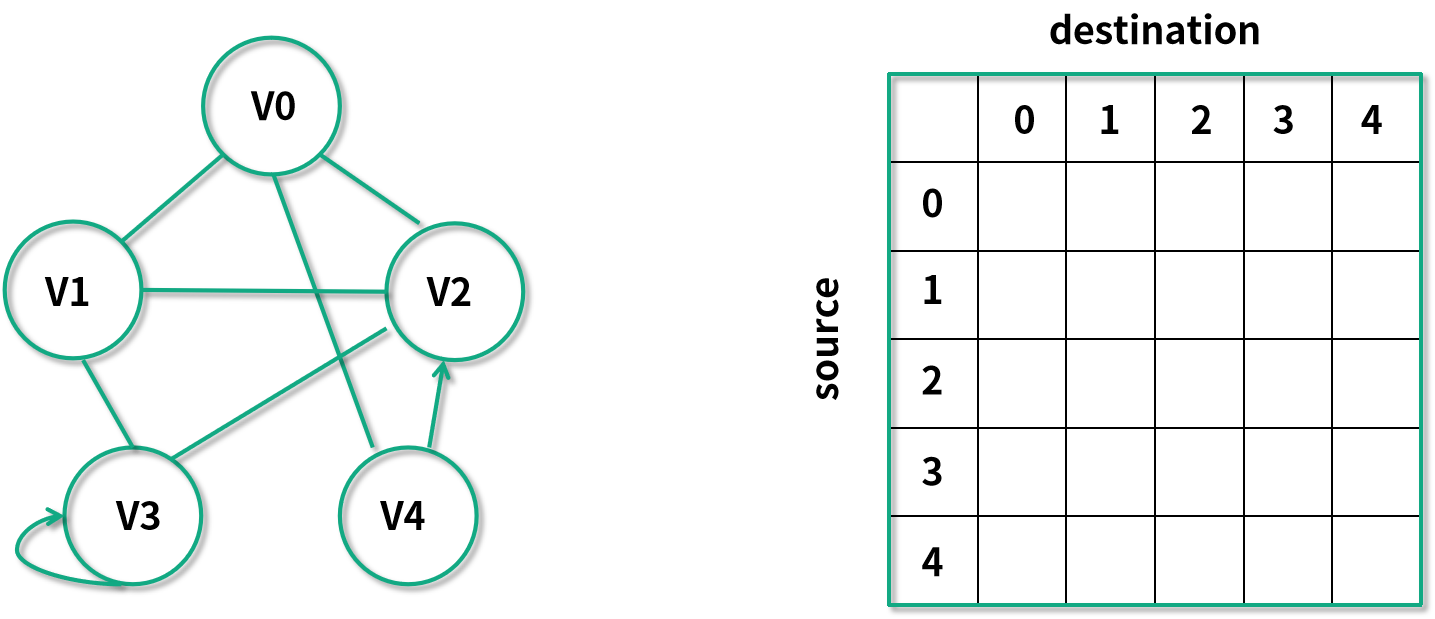
在上一講中我們學習了圖的基本概念，以及圖是如何在 Spark 這樣的大數據框架中大展身手的，不過核心內容是有向無環圖（DAG）的應用。你一定想知道 Spark 建立了 DAG 之后又如何執行數據處理的呢？這一課時我來為你揭曉。 #### 圖的實現方式 我們先回顧一下之前講解的兩種圖的實現方式，一種是鄰接矩陣法，另一種是鄰接鏈表法。這兩種實現方式將會影響到我們后面算法的應用。 使用鄰接矩陣法的基本思想是開一個超大的數組，用數組中間元素的 true/false 來表達邊，有 V 個節點的圖，需要一個 V × V 大小的數組。下面這個例子中有 V0 ~ V4 總共 5 個節點，可以看到我們已經畫出了一個 5 × 5 的二維數組 G。如果有從 Vi 指向 Vj 的邊，那么 G[i][j] = true，反之如果沒有邊，則 G[i][j] = false。 有 V4 指向 V2 的邊，那么 G[4][2] = true。V0 和 V2 之間的邊是無向的，也就是說我們需要 G[0][2] = true 同時 G[2][0] = true。再看到 V3 有指向自己的邊，所以 G[3][3] 也是 true。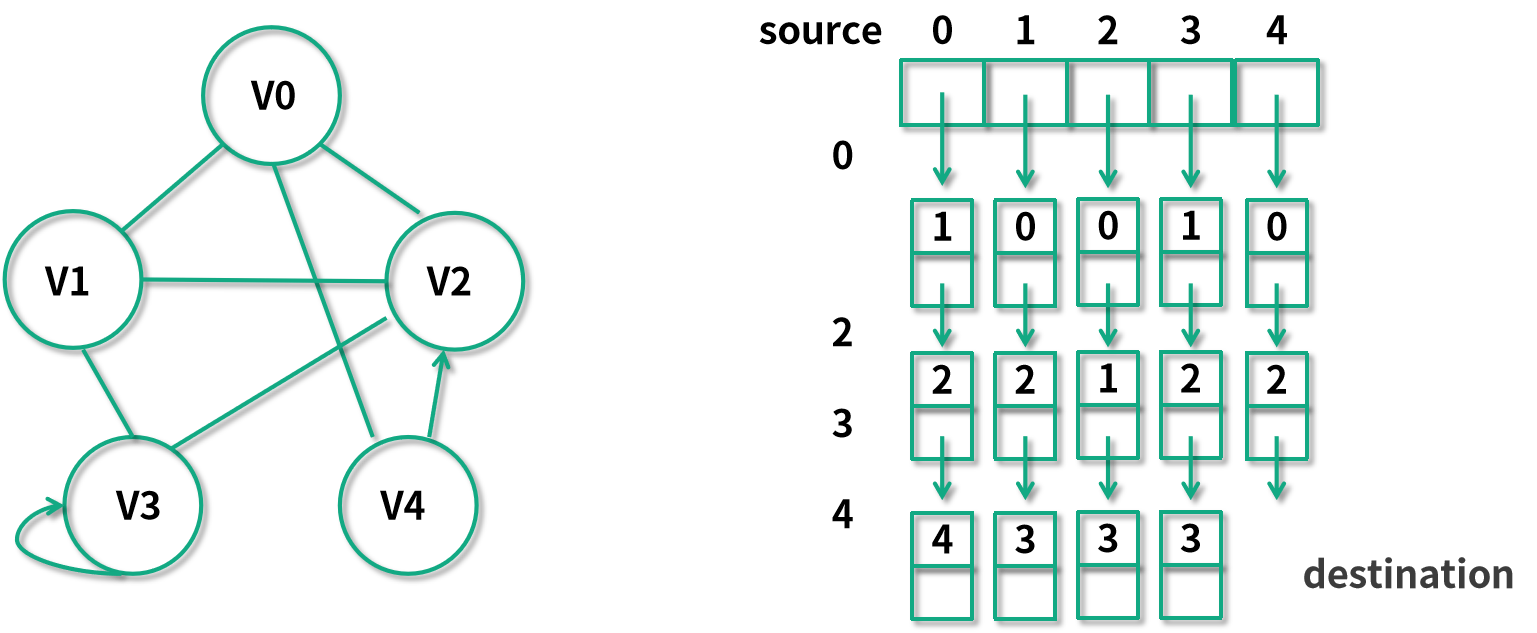  鄰接鏈表法的核心思想是把每一個節點所指向的點給存儲起來。比如還是上面的例子，如果我們用鄰接鏈表法表達的話，則需要一個含 5 個元素的數組，用來存儲這樣的 5 個節點，然后每個節點所指向的點都會維護在一個鏈表中。比如，V0 指向了 V1、V4、V2 三個節點，那在內存中就會有從 0 指向 1 接著指向 2、指向 4 這樣的一個鏈表。同理我們看到 V4 指向了 V0 和 V2，在內存中就要維護一個 4→0→2 的單向鏈表。  #### 圖的拓撲排序 什么是拓撲排序呢？拓撲排序指的是對于一個有向無環圖來說，排序所有的節點，使得對于從節點 u 到節點 v 的每個有向邊 uv，u 在排序中都在 v 之前。拿我們之前講過的西紅柿炒雞蛋這個例子來說吧。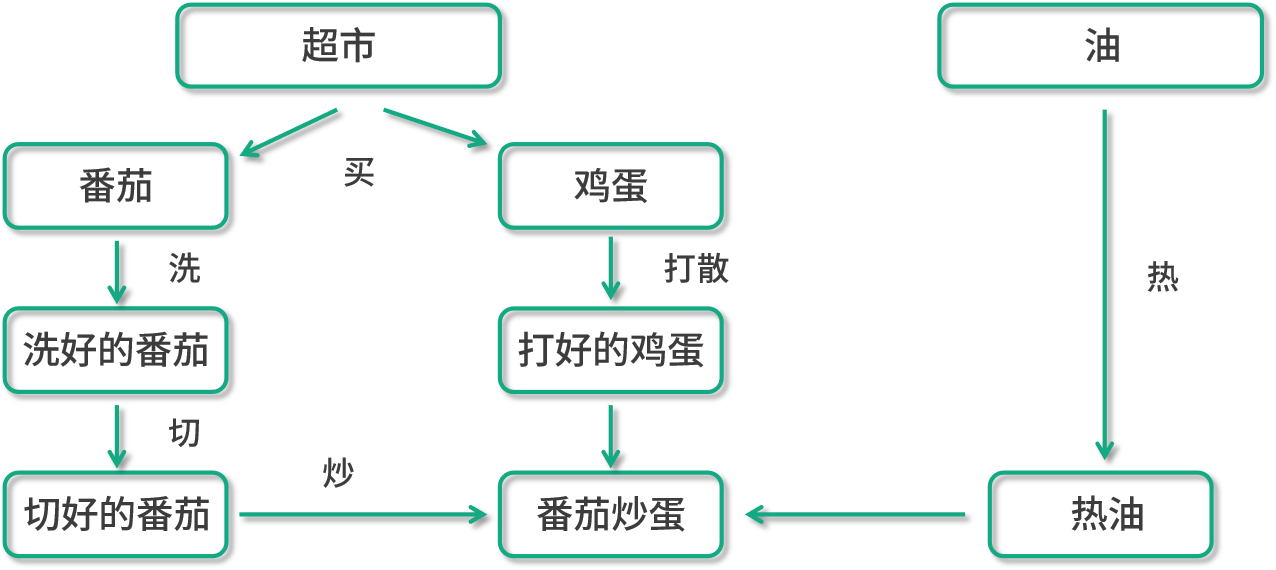  一個合法的拓撲排序，必須使得被依賴的任務首先完成。在我們西紅柿炒雞蛋這個菜的加工過程中，要保證打雞蛋在炒雞蛋之前，買番茄在洗番茄之前，因為炒雞蛋依賴于打雞蛋，在我們的圖中有打雞蛋指向炒雞蛋的邊。 所以說一個合理的拓撲排序是能夠保證有依賴關系的任務能夠被合理完成。不如你思考一下為什么拓撲排序只適用于有向無環圖呢？ 我們來看一個經典的例子，那就是“雞生蛋、蛋生雞”。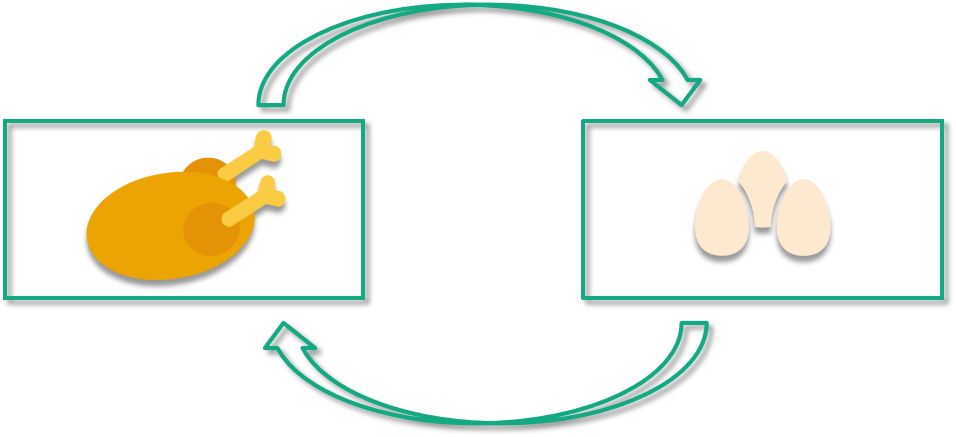  先有雞還是先有蛋 （Chicken Egg Dilemma）就是一個無法被拓撲排序的有環圖，因為雞依賴于蛋，蛋又依賴于雞，你無法把雞排在蛋前面，也不能把蛋排在雞的前面。  再來看一個經典的可以被拓撲排序的例子。我們常說：“等我有錢要去干嘛干嘛。”這里面隱含的一個有向無環圖就是錢指向了你想做的事情，那么我們就很容易的得出一個合理的拓撲排序，要把錢排在你想做的事情之前。 #### 拓撲排序的實現方式 首先我們來看看兩個簡單的概念，圖的入度和出度。一個有向圖的入度指的是終止于一個節點的邊的數量；有向圖的出度指的是始于一個節點的邊的數量。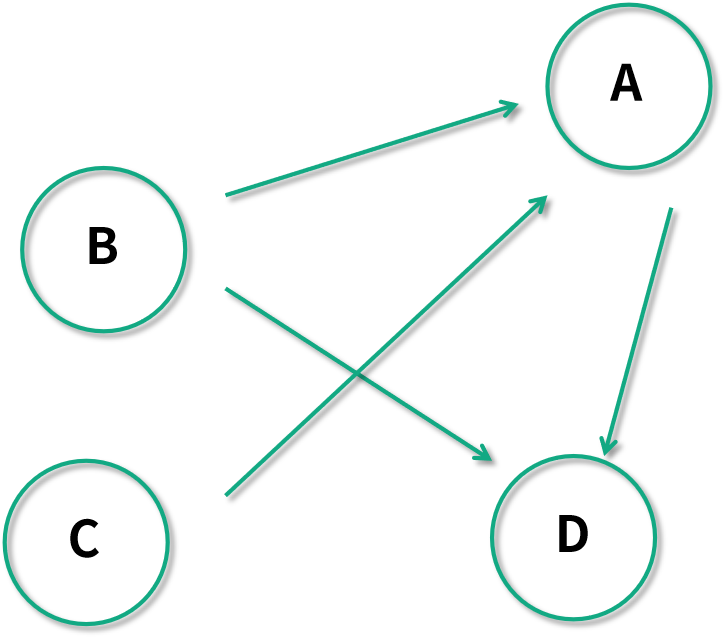以下圖為例：  節點 A 的入度為 2，節點 B 的入度則為 0；而節點 B 的出度為 2，節點 D 的出度則為 0。 卡恩算法是卡恩于 1962 年提出的算法，它其實是貪婪算法的一種形式。簡單來說就是，假設 L 是存放結果的列表，我們先找到那些入度為零的節點，把這些節點放到 L 中，因為這些節點沒有任何的父節點；然后把與這些節點相連的邊從圖中去掉，再尋找圖中入度為零的節點。對于新找到的這些入度為零的節點來說，他們的父節點都已經在 L 中了，所以也可以放入 L。 重復上述操作，直到找不到入度為零的節點。如果此時 L 中的元素個數和節點總數相同，則說明排序完成；如果 L 中的元素個數和節點總數不同，則說明原圖中存在環，無法進行拓撲排序。下面我們來看看這個算法的偽代碼： ``` L?←?Empty?list?that?will?contain?the?sorted?elements S?←?Set?of?all?nodes?with?no?incoming?edge while?S?is?non-empty?do ????remove?a?node?n?from?S ????add?n?to?tail?of?L ????for?each?node?m?with?an?edge?e?from?n?to?m?do ????????remove?edge?e?from?the?graph ????????if?m?has?no?other?incoming?edges?then ????????????insert?m?into?S if?graph?has?edges?then ????return?error???(graph?has?at?least?one?cycle) else? ????return?L???(a?topologically?sorted?order ``` 怎么樣？學到這里你就掌握了 Spark 運算引擎的核心，即拓撲排序。一旦 Spark 確立好了大數據處理的有向無環圖，它就會對數據處理步驟進行拓撲排序，找到合理的處理順序。 #### 圖的最短路徑 圖的最短路徑也是非常常見的圖的應用，最短路徑顧名思義就是在一個有權重的圖中，找到兩個點之間權重之和最短的路徑。 舉例來說下，圖中所有節點都是不同的城市，每一條邊都是連接城市之間的道路距離。比如 1 號節點是武漢，那么我們想要快速地把醫療物資送到武漢的話，就需要找到通向武漢最短的路線。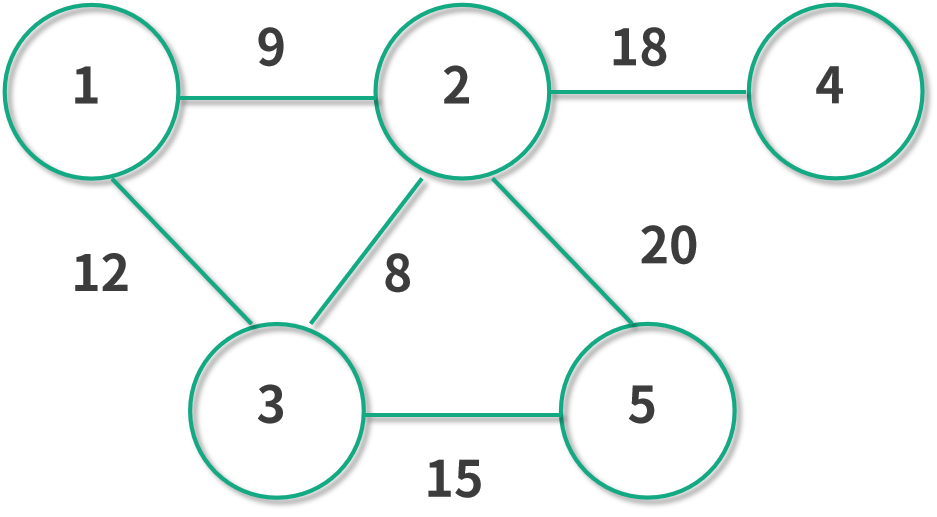  假如我們有一大批口罩在 5 號城市，想要送往武漢的話可以選擇走 5-2-1 這條路線，或者 5-3-1 這條路線，甚至 5-2-3-1 等很多路線。在這個例子中我們很容易發現，5-2-1 這條路線的總距離是 20 + 9 = 29，5-3-1 這條路線的總距離是 12+15 = 27，可見我們應該選擇 5-3-1 這個路線。 我們怎樣讓計算機找到最短路徑呢？這便是大名鼎鼎的 Dijkstra 算法。 最經典的 Dijkstra 算法原始版本僅適用于找到兩個固定節點之間的最短路徑，后來更常見的變體固定了一個節點作為源節點，然后找到該節點到圖中所有其他節點的最短路徑，從而產生一個最短路徑樹。我們這一講會重點講解最經典的也就是真正業界應用最多的場景，即兩個節點都固定。 這個算法是通過為每個節點 v 保留當前為止所找到的從 s 到 v 的最短路徑來工作的。在初始時，原點 s 的路徑權重被賦為 0（即原點的實際最短路徑 = 0），同時把所有其他節點的路徑長度設為無窮大，即表示我們不知道任何通向這些節點的路徑。當算法結束時，d[v] 中存儲的便是從 s 到 v 的最短路徑，或者如果路徑不存在的話，則是無窮大。 偽代碼如下所示： ``` ?function?Dijkstra(Graph,?source): ??????create?vertex?set?Q ??????for?each?vertex?v?in?Graph:????????????? ??????????dist[v]?←?INFINITY?????????????????? ??????????prev[v]?←?UNDEFINED????????????????? ??????????add?v?to?Q?????????????????????? ??????dist[source]?←?0???????????????????????? ?????? ??????while?Q?is?not?empty: ??????????u?←?vertex?in?Q?with?min?dist[u]???? ?????????????????????????????????????????????? ??????????remove?u?from?Q? ?????????? ??????????for?each?neighbor?v?of?u:???????????//?only?v?that?are?still?in?Q ??????????????alt?←?dist[u]?+?length(u,?v) ??????????????if?alt?<?dist[v]:??????????????? ??????????????????dist[v]?←?alt? ??????????????????prev[v]?←?u? ??????return?dist[],?prev ``` #### 總結 這一課時我們學習了兩種圖在應用中最重要的算法，先是圖的拓撲排序，揭開了 Spark 最核心的機密算法，之后是圖的最短路徑算法，將會在下一講中應用到。