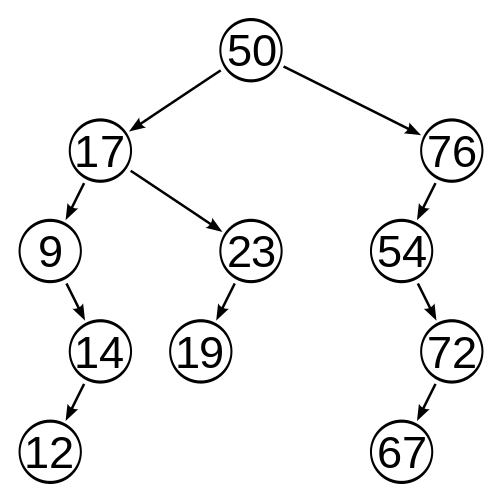
不知你是否還記得在第 9 講中，我們講了“為什么需要樹”，是因為人們想要更好的檢索信息。這時候你一定會有疑問：可是我們到現在都還沒講怎樣用樹查找信息啊？ 要用樹檢索信息，就不得不掌握平衡樹，平衡樹的全稱是平衡二叉查找樹（Balanced Binary Search Tree，簡稱 Balanced Tree）。為什么可以把“二叉”這個特性省略呢？是因為沒有二叉這個很強的約束條件，其實平衡的意義也不是很大，為什么呢？下面且聽我細細道來。 #### 二叉查找樹 （BST） 我們先來看二叉查找樹（Binary Search Tree，簡稱 BST），二叉查找樹顧名思義就是有查找功能的二叉樹，還是先來看一個例子吧：  ? 上圖是一顆以 50 節點為根的二叉查找樹，規范的來說： * 二叉查找樹是一棵二叉樹，也就是說每一個節點至多有 2 個孩子，也就是 2 個子樹。 * 二叉查找樹的任意一個節點都比它的左子樹所有節點大，同時比右子樹所有節點小。 我們來驗證一下上圖這個例子是不是符合二叉查找樹的定義。可以先看 50 這個根節點，它只有兩個孩子，它的左子樹的節點比如 17，50 是大于 17 的，又比如 19，50 也大于 19；右孩子呢，有 76，50 小于 76，還有比如 72，50 也小于 72。所以 50 這個節點符合了關于孩子個數，以及孩子與自己之間大小的定義了。 我們再看一個節點，比如 23 這個節點，它只有一個孩子，也可以說，它唯一的后代是 19，19 小于 23，完美。看來我們這棵樹的的確確是一個二叉查找樹。 #### 在二叉查找樹中搜索節點 知道了二叉查找樹的定義，我們一定要探尋它的究竟！為什么二叉查找樹定義奇怪的特性，究竟有什么用？其實都是為了方便搜索節點！ 你看，因為我們已經知道了所有左子樹的節點都小于根節點，所有右子樹的節點都大于根節點。當我們需要查找一個節點的時候，如果這個節點小于根，那我們肯定是去左子樹中繼續查找，因為它不可能出現在右子樹中了，右子樹的所有節點必須大于根。反過來說，如果想要查找的值大于根呢？我們就只需要去右子樹中查找即可。 是不是搜索變得很簡單了？也很容易用遞歸的方式實現： ``` TreeNode*?Search(TreeNode*?root,?int?key)?{? ????if?(root?==?nullptr?||?root->key?==?key)?{ ???????return?root;? ????} ????? ????if?(root->key?<?key)?{ ??????return?Search(root->right,?key);? ????} ?? ????return?Search(root->left,?key);? } ``` 這是不是讓你想起了經典的二分查找法？確實很類似。這樣在二叉查找樹中的搜索形象的說，就是順著根節點往下擼。上面 Search() 方法的每一次調用都會在樹中往下移動一層。所以我們可以想到這樣的算法時間復雜度，就是樹的高度 O(h)。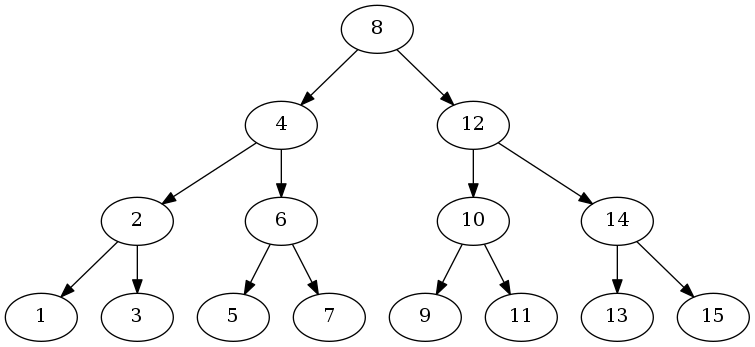 讓我們想象一個最優情形，如果二叉查找樹是完美對稱平衡的，如圖中所示：  這棵樹的高度是 O(log n)，n 是這棵樹的節點數量。無論搜索哪個節點，我們最多需要運行上面的 Search() 方法 O(log n)，怎么樣？是不是有種逃不出如來佛祖手掌心的感覺。 再讓我們看一個最壞的情況，如果二叉查找樹每一個節點都只有一個孩子呢？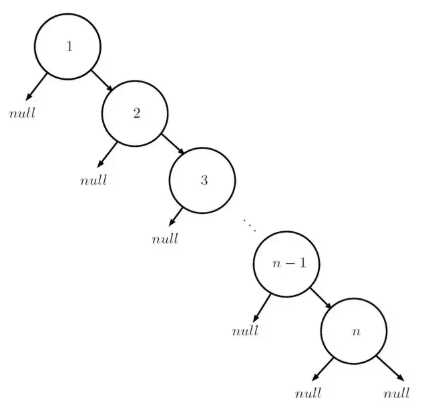如圖中所示：  這樣的二叉樹退化成了一個一維鏈表，最壞情況是需要從第一個節點查找到第 n 個節點，時間復雜度就成了 O(n) 了。 到這里我們就明白了，二叉查找樹的搜索特性聽起來很美好，但實際上如果這棵樹的形狀長得不好，數據偏向一邊而不平衡，也無從談起高效的查詢特性啊，那我們怎樣維護好一個二叉查找樹的高度和形狀呢？這就是接下來要講的包括紅黑樹和 AVL 樹在內的平衡樹。 #### 平衡樹 平衡樹，就是說一棵樹的數據結構能夠維護好自己的高度和形狀，讓形狀保持平衡的同時，高度也會得到控制。平衡樹的定義其實是比較粗糙的，屬于一個愿景。具體實現平衡的方式就要深入具體平衡樹的種類了。 紅黑樹被定義成： * 一棵二叉樹，每一個節點要么是紅色，要么是黑色 * 根節點一定是黑色 * 紅節點不能有紅孩子 每條從根節點到底部的路徑都經過同樣數量的黑節點 看個例子，這棵紅黑樹的根節點值是 13，是一個黑色節點。比如紅節點 8 的兩個孩子是黑色節點 1 和 11，因為紅節點不能有紅孩子。可以看到，從根節點 13 通向 22 的路徑，經過了 13 和 25 這兩個黑節點；從根節點 13 通向 11 的路徑，經過了 13 和 11 這兩個黑節點。因為最后一個定義就是說：  滿足這些定義的紅黑樹可以被數學證明樹的高度為 O(log n)。要實現一棵紅黑樹是非常難的，其中有許多節點插入 / 刪除需要用到旋轉等操作細節，我們在這一講中無法展開講解，可自行查閱資料學習。 還有一種平衡樹叫 B 樹，B 樹的每個節點可以存儲多個數值，但是要求： * 所有葉子節點的深度一樣 * 非葉子節點只能存儲 b － 1 到 2b － 1 個值 * 根節點最多存儲 2b － 1 個值 紅黑樹可以被理解成 order 為 4 的一種特殊 B 樹，稱為 2-3-4 樹，之所以稱為 2-3-4 樹，是因為每個有子樹的節點都只可能有兩個，或者 3 個，或者 4 個子節點。 類似想法的平衡樹實現還有很多，比如 AVL 樹，由它的發明者們的名字首字母命名，分別是 Adelson-Velsky-Landis，它的定義很簡單，任意一個節點的左右子樹高度最多相差 1。 由于篇幅有限，我們就不再一一展開各種平衡樹的講解了，可自行查閱資料學習。 #### Log-Structured 結構 在計算機存儲數據結構的發展中，Log-Structured 結構的誕生為許多文件系統或者是數據庫打下了堅實的基礎。比如說，Google 的三駕馬車之一，Bigtable 文件系統的底層存儲數據結構采用的就是 Log-Structured 結構，還有大家所熟知的 MongoDB 和 HBase 這類的 NoSQL 數據庫，它們的底層存儲數據結構其實也是 Log-Structured 結構。 而 Log-Structured 結構其實和平衡樹有著莫大的關系，因為在這些框架應用里面，通常都會使用平衡樹來優化數據的查找速度。在這一講中，我會先介紹什么是 Log-Structured 結構，而在下一講中，再詳細介紹平衡樹數據結構是如何被應用在 Log-Structured 結構中的。 我們先來看看一個常見的問題應用。假設一個視頻網站需要一個統計視頻觀看次數的功能，如果給你來設計的話，會采用哪種數據結構呢？你可能會覺得這并不難，我們可以運用哈希表這個數據結構，以視頻的 URL 作為鍵、觀看次數作為值，保存在哈希表里面。所有保存在哈希表里面的初始值都為 0，表示并無任何人觀看，而每次有人觀看了一個視頻之后，就將這個視頻所對應的值取出然后加 1。 剛開始的時候，這個設計思路可能運行得很好。可當用戶量增大了之后，會發現在更新哈希表的時候必須要加鎖，不然的話，大量的這種并行 +1 操作可能會覆蓋掉各自的值。比方說，在同一時間，有兩個用戶都觀看了一個視頻，它們都根據視頻的 URL 在哈希表中取出了觀看次數的值 0，在更新操作 +1 了之后，都把 1 這個值保存在了哈希表中，而實際上，哈希表中的值應該是 2。 不難發現，這種操作的瓶頸其實是在更新操作，也就是寫操作上。那有沒有方法可以不用顧及寫操作的高并發問題，同時也可以最終獲得一個準確的結果呢？答案就是使用 Log-Structured 結構。 Log-Structured 結構，有時候也會被稱作是 Append-only Sequence of Data，因為所有的寫操作都會不停地添加進這個數據結構中，而不會更新原來已有的值，這也是 Log-Structured 結構的一大特性。 我們來看看在采用了 Log-Structured 結構之后，在上面的統計視頻網站觀看次數的應用中，底層的數據結構變成怎么樣了。 假設現在網站總共有三個視頻，URL 分別就是 A、B 和 C，那一個可能的數據結構圖就如下圖所示：  從上圖中可以看到，這樣的數據結構其實和數組非常像，數組里的值就保存著 URL 和 1，每次有新用戶觀看過視頻之后，就會將 URL 和 1 加到數組的結尾。在上面的例子中，我們只需要遍歷一遍這個數組，然后將不同的 URL 值加起來就可以得到觀看的總數，例如 A 的觀看總數為 8 次，B 為 3 次，C 為 5 次。 這其實就是 Log-Structured 結構的本質了，不過細心的你應該可以發現了，這樣一個最基本的 Log-Structured 結構，其實在應用里會有很多的問題。比如說，一個數組不可能在內存中無限地增長下去，我們要如何處理呢？如果每次想要知道結果，就必須遍歷一遍這樣的數組，時間復雜度會非常高，那該怎么優化呢？平衡樹是如何被應用在里面的呢？所有這些問題的答案我都會在下一講中為你講解。