在介紹樹之前我們先回顧一下之前學了哪些數據結構？以及還有哪些問題沒法用之前的數據結構解決？這是我們在學習任何技術知識的一個重要習慣，思考一下假如沒有這個技術會怎么樣，這個技術解決了哪些以前不能解決的問題。 #### 有了數組和鏈表，為什么還需要樹 在第 01、02 講中我們一起學了數組，數組是一個很容易編程實現的靜態數據結構，可以很好的支持隨機訪問。鏈表相對來說多了一些動態特性，鏈表適合的應用場景為需要比較頻繁的增、刪和更新操作。鏈表的時間復雜度特性我們也介紹了，相比數組，它的缺點是隨機訪問的時間復雜度為 O(n)。 基于數組和鏈表也有很多衍生出的數據結構，比如隊列和堆棧，隊列是先進先出，而堆棧是先進后出，它們可以被看作是定制化的數組或者隊列，用來解決一些特定問題。之后我們又介紹了哈希表數據結構，哈希表的重要應用場景是快速查詢和更新，正如我們之前學習的那樣，哈希表的查詢和更新時間復雜度都是均攤 O(1)。 數組和鏈表的局限性正是來自于它們的線性特點。當你需要在數組或者鏈表中查詢一個元素時，則需要從頭到尾遍歷這個列表，此時的時間復雜度為 O(n)。試想一個含有 1 萬個元素的集合，如果存儲在一個數組或者鏈表里面，那么進行一萬次查詢需要多少時間呢？其時間復雜度是 O(108)，這取決于你的內存訪問速度和 CPU 速度，可能需要十幾分鐘的時間。 在現代的互聯網應用中，1 萬的 QPS 非常常見。如果要支撐每秒高達 1 萬的訪問，顯然如果僅僅使用數組和鏈表是不夠的。 所以樹應運而生，這也是我們這一講要講的內容。樹相比數組和鏈表，其抽象表達元素之間的關系更為復雜。我們一起來看看吧！ #### 樹的定義和例子 樹由節點和邊連接組成，與數組和鏈表不同，它是一種非線性的數據結構。在學習樹的規范而枯燥的數學定義之前，我們先來看一個例子吧！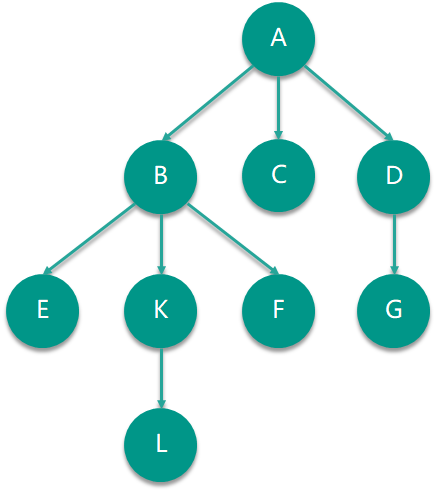  在上圖中，A 是這棵樹的根。除了根節點外的節點都有且僅有一條指向自己的邊，這個邊的方向代表了父節點指向了子節點。比如，A ?是 B、C、D 的父節點，B 又被稱為 A 的子節點，同時 B 也是 E、F、K 的父節點。 每個節點都可以連接著任意數量的子數（包括 0 個），沒有子節點的節點也被稱作葉子節點，在上圖例子中，C、E、F、L、G 都是葉子節點。共享同樣父節點的節點被稱作兄弟節點，在上圖例子中，B、C、D 就是兄弟節點。 一個節點的深度是從根節點到自己邊的數量，比如 K 的深度是 2。 節點的高度是從最深的節點開始到自己邊的數量，比如 B 的高度是 2。一棵樹的高度也就是它根節點的高度 樹的遞歸定義是： n（n>=0）個節點的有限集合，其中每個節點都包含了一個值，并由邊指向別的節點（子節點），邊不能被重復，并且沒有節點能指向根節點。廣義的樹中，節點可以有 0 個或者多個子節點。而在后面章節中將介紹的二叉樹等就是廣義樹中的特殊類型（每個節點有兩個子節點）。 廣義的樹可以用來表達有層次結構的數據關系，比如文件系統（File System）是一個有層次關系的集合，文件系統中每一個目錄（Directory）可以包含多個目錄，沒有子目錄的葉子節點也就是文件（File）了。 公司里的匯報結構也可以用樹來表達，比如我的手下有小明和小張兩個人匯報工作，那么小明和小張都是我的子節點，小張下面還有 1 個程序員小李，沒有人匯報給小李那么小李就是一個葉子節點。在這樣一個匯報結構中我是這棵樹的根節點。 正如這一講開頭所說的那樣，人們設計樹這樣的數據結構是為了能夠更好的組織數據、快速地查找數據。比如在文件系統中我們要查找一張照片，只需要找到照片文件夾再查詢就可以了。 比如在公司組織架構中，假如我是負責網頁平臺的負責人，也就是網頁平臺子樹的根節點，那么如果網頁出了問題，CEO 很有可能就直接就來找我了，因為我是根節點，如果要讓 CEO 去查詢所有的程序員葉子節點，可能節點數量太多而無法遍歷了。這也是為什么一個公司不能用鏈表這樣的方式組織，那樣的話，我作為 CEO，小張匯報給我、小李匯報給小張、小明再匯報給小李，最后只剩下唯一的葉子節點也就是鏈表最后一個元素在干活了。 #### 樹的編程實現方式 樹的實現方式有很多種，在這里介紹兩種常見的實現方式，一種是基于鏈表的實現，另一種是基于數組的實現。對的，你沒有看錯，正是基于我們之前學習的數組和鏈表，這也是為什么在專欄開始就和你強調數組和鏈表是數據結構大廈的基石。高級的數據結構離不開對于這兩種基礎數據結構的深入理解。 基于鏈表的實現一般是每一個節點類型維護一個子節點指針和一個指向兄弟節點的鏈表，我們把它稱作左孩子兄弟鏈表法。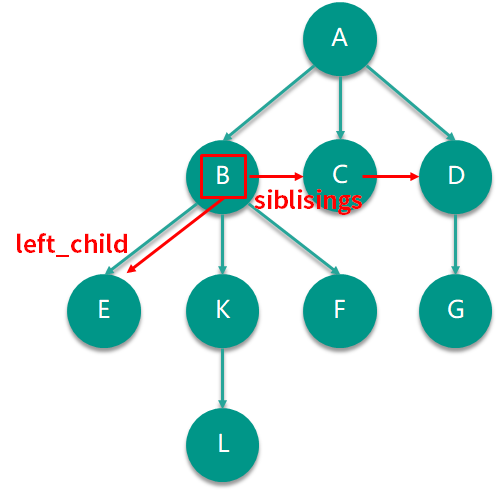代碼是這樣的： ``` class?TreeNode?{ ??????Data?data; ??????LinkedList?siblings; ??????TreeNode?left_child; } ``` 在我們上面圖樹的例子中，如果用左孩子兄弟鏈表法實現節點 B 的話，來看看節點 B 在這個代碼中會是什么樣子呢？如下圖所示，節點 B 的 siblisings 節點是一個指向 C 接著指向 D 的鏈表，節點 B 的 left_child 節點則指向 E。  另一種基于數組的實現方式是每一個節點維護一個包含它所有子節點的數組，我們把它稱作孩子數組法。 ``` class?TreeNode?{ ??????Data?data; ??????ArrayList?children; } ``` 我們也來看看這種孩子數組法中在實際例子中的樣子吧！如下圖所示，同樣是節點 B，利用孩子數組法實現的話，需要維護一個包含 E、K、F 的數組。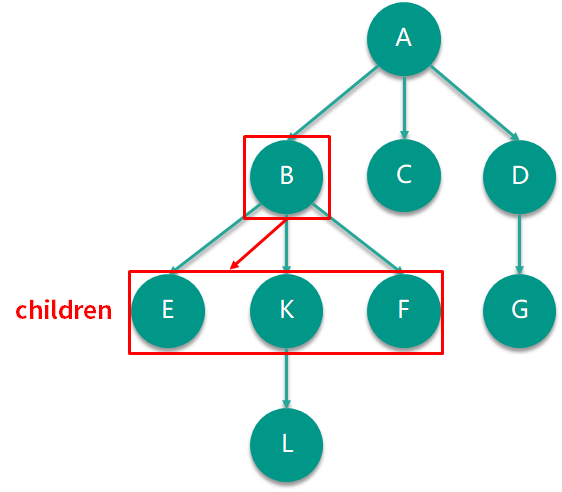  看來這兩種方式實現起來似乎都挺容易的，實際并不是這樣的。你能看出這兩種實現方式的差異嗎？ 在實現一個樹的編程中，最容易犯的錯誤在于內存管理和節點的增、刪、改。 為了更好的闡述這里的內存管理以及增刪改問題，我們用 C++ 進行示范，一種簡單幼稚的孩子數組法實現是這樣的: ``` class?TreeNode?{ ??????Data?data; ??????std::vector<TreeNode>?children; }; ``` 可以發現，所有子節點的內存都是由父節點管理，也就是說當父節點被刪除時，子節點的內存也會被自動清理。那就造成了一個很嚴重的問題，我們很難方便地刪除任意一個非葉子節點。所以事實上用孩子數組實現的話我們往往只能維護一組子節點的指針，像是這樣： ``` class?TreeNode?{ ??????Data?data; ??????std::vector<TreeNode*>?children; }; ``` 這就造成了另一個問題，子節點的內存由誰來管理呢？所以一個解決辦法是除了實現這樣一個 TreeNode 類，再去實現一個 NodePool 類用來管理所有的節點內存。例如下面代碼，用一個簡單的動態數組維護內存： ``` class?NodePool?{ ??std::vector<TreeNode>?nodes; } ``` 另一個解決辦法則是模仿鏈表的內存管理，在左孩子兄弟鏈表法中比較容易實現，因為它實際上就是一個二叉的鏈表。 除了內存管理問題，樹節點的插入、刪除也是難點。如果你還記得之前學習的數組和鏈表基本操作，就能知道數組的隨機元素增刪是 O(n) 的復雜度，而鏈表是 O(1)。在這里樹的實現方式也是類似。 在左孩子兄弟鏈表法中，插入一個樹節點的復雜度是 O(1)，相當于是在 siblings 鏈表中插入一個元素，或者是增加一個 left_child 節點。而在孩子數組法中插入一個節點和數組插入元素類似，需要挪動其后的所有節點，則是 O(n) 的復雜度。 刪除節點相比插入節點更為復雜一些，同樣的，在孩子數組法中，刪除單個節點的復雜度是 O(n)，因為你需要去拷貝這個節點的子樹到上層節點。在左孩子兄弟鏈表法中，刪除單個節點的復雜度為 O(1)，你只需要去重新整理幾根指針引用就可以了。 那么現在看來左孩子兄弟鏈表法各項表現都優于孩子數組法，的確如此，左孩子兄弟鏈表法是樹的教科書范式實現方法。但在實際應用中我們還是常常見到孩子數組法，為什么呢？因為孩子數組法從 API 使用角度更為簡單，使用者可以隨機訪問任意孩子。特別當我們想要提供一個數組的只讀的鏡像時（Read-Only View），孩子數組法可以作為 API 提供，但是背后可修改的樹仍然是由更為復雜的私有方法實現的。 * [ ] 樹的遍歷和基本算法 除了樹的增、刪、改，樹最最常見的操作就是查找操作，也就是遍歷。如果沒有遍歷，增、刪、改根本無從談起，因為你都不知道去操作哪個節點！樹的遍歷根據根節點的訪問順序，可以分為前序遍歷、后續遍歷和按層遍歷等多種。所謂前序遍歷用偽代碼表示就是： * 先訪問根節點N * 遞歸訪問N的子樹 你一定猜到了所謂后續遍歷是相似的： * 遞歸訪問N的子樹 * 后訪問根節點N 按層遍歷呢？就是從上到下、從左到右訪問。例如，在上面的樹的例子中，按層遍歷的結果是：A, B, C, D, E, K, F, G, L。 我們來看看在左孩子兄弟鏈表法中怎樣實現前序遍歷吧！ ``` class?TreeNode?{ ??TreeNode*?left_child; ??TreeNode*?sibling; } void?PreorderVisit(TreeNode?root)?{ ??Visit(root); ??for?(TreeNode*?child?=?root->left_child;?child?!=?nullptr;?child?=?child->sibling)?{ ????PreorderVisit(child); ??} } ``` #### 總結 這一講到這里你已經了解了我們為什么需要樹，掌握了樹的概念和定義，更重要的是比較了樹的實現方式和遍歷方法，樹的遍歷復雜度相信你肯定也已經看出來了，是 O(n)。如果你不忘初心，還記得在開頭說的樹是為了更快的方便數據查找，此時你一定有疑問，好像樹并沒有更高效的數據查詢啊？這個呢，我們將會在第 11 講的二叉查詢樹章節中展開講解，在講二叉查詢樹之前我們也會先講解廣義樹的重要應用。