在上一講中，我們一起學習了平衡樹和?Log-Structured?結構的基本概念，那么今天我們就來延續上一講的問題，繼續探討如何優化?Log-Structured?結構，以及通過結合平衡樹之后才產生的另外一種數據結構——LSM?樹。 首先我們一起來回顧一下在上一講中所遺留的問題。在通過?Log-Structured?結構設計視頻網站瀏覽次數的功能后，底層的數據結構就如下圖所示：  這種方法存在的一個問題，就是當我們不斷地添加新數據進去之后，所占用的空間會越來越大，而且遍歷整個數據結構的時間也隨之越來越長。這時候，我們就可以通過一種叫?Compaction?的方法，把數據合并，Compaction?方法其實也是很多?NoSQL?架構中的一個重要優化過程。下面我就來詳細講講整個流程。 #### Log-Structured?結構的優化 首先，可以定義一個大小為?N?的固定數組，我們稱它為?Segment，一個?Segment?最多可以存儲?N?個數據，當有第?N+1?個數據需要寫入?Log-Structured?結構的時候，我們會創建一個新的?Segment，然后將?N+1?個數據寫入到新的?Segment?中。 以下圖為示，我們定義一個?Segment?的大小為?16，當?Segment 1?寫滿了?16?個數據之后，會將新的數據寫入到?Segment 2?里。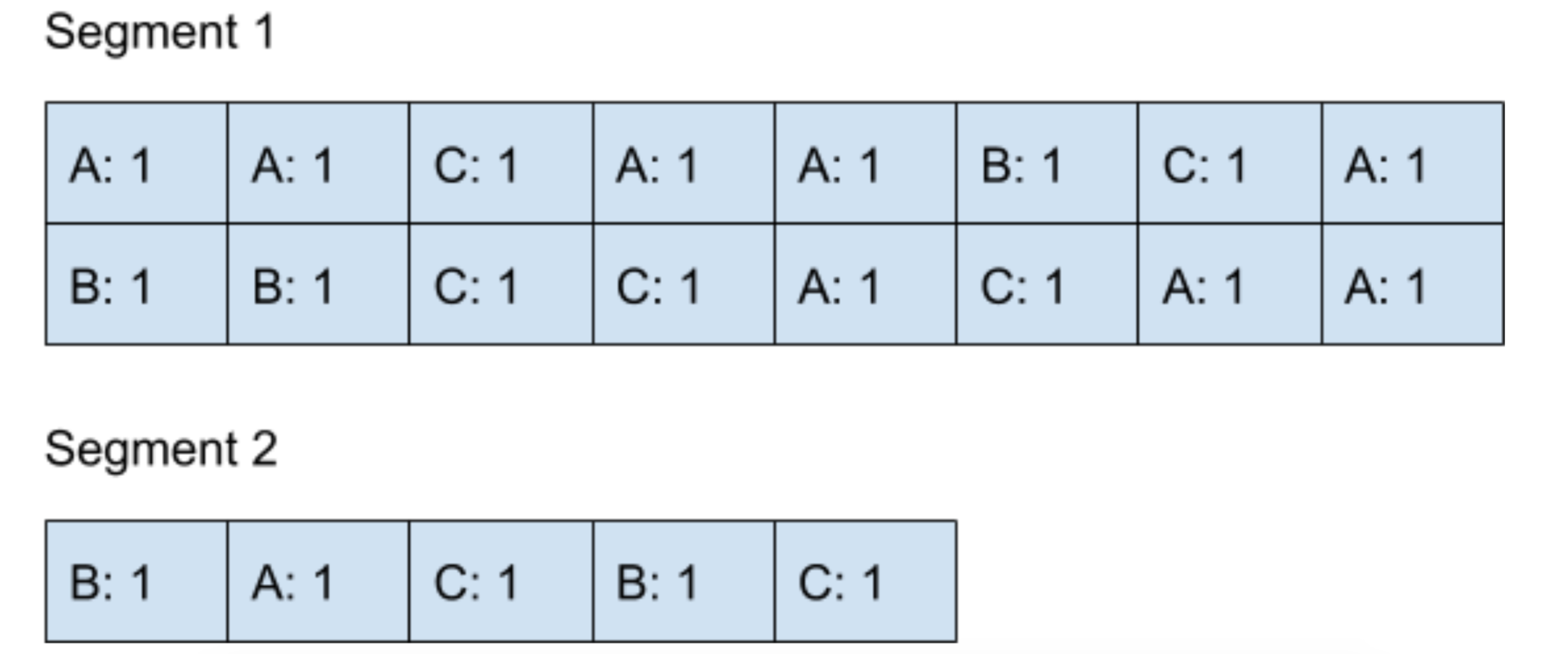  說到這里，我們的?Log-Structured?結構還是一直在往內存里添加數據，并沒有解決最終會消耗完內存的問題。這時候就到?Compaction?大顯身手的時候了，在當?Segment?到達一定數量的時候，Compaction?會通過后臺的線程，把不同的?Segments?合并在一起，我們以下圖為例來說明一下。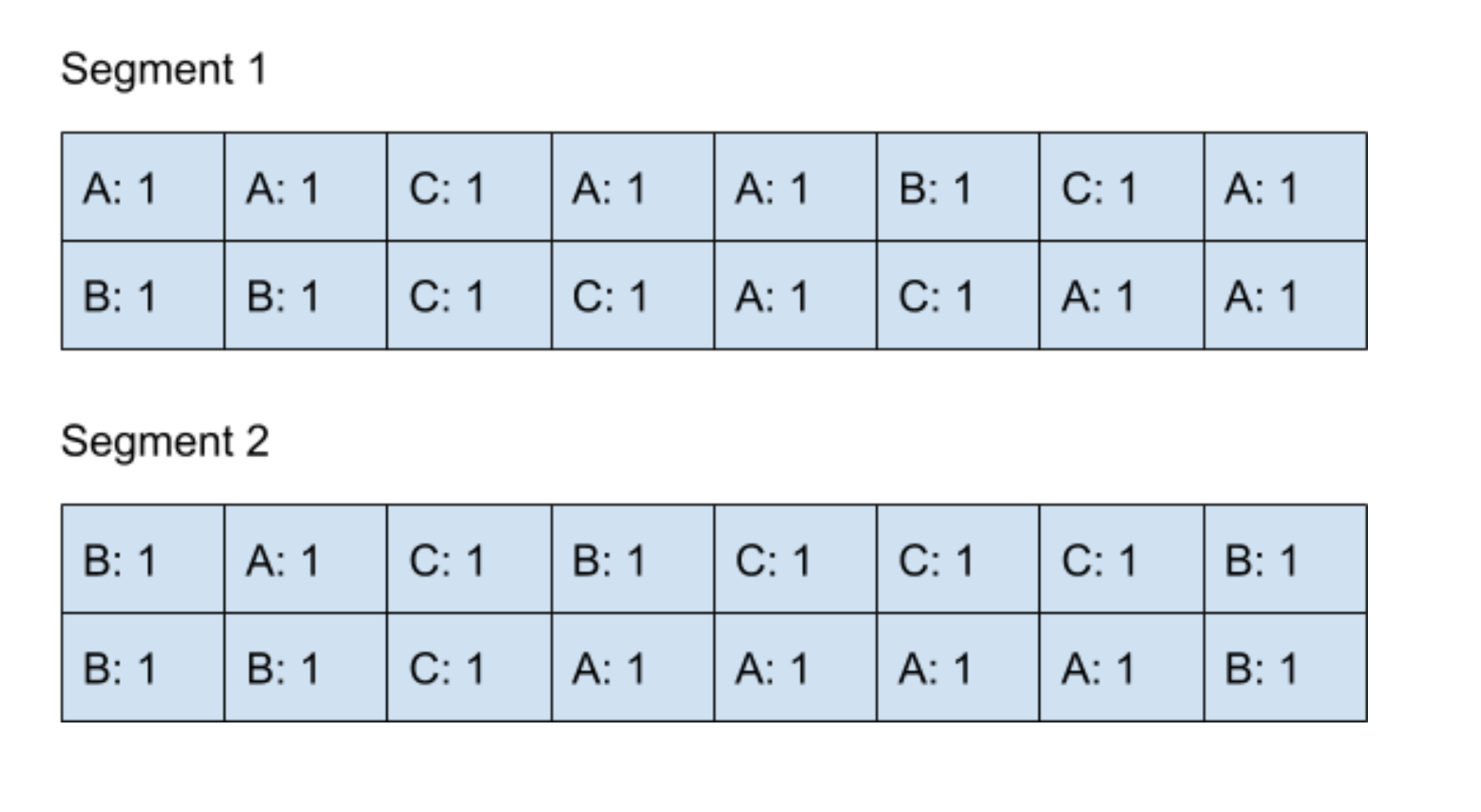 假設我們定義當?Segment?的數量到達兩個的時候，后臺線程就會執行?Compaction?來合并結果。  ? ? ? ? 執行完?Compaction?之后，內部的數據結構圖如下圖所示：  ? ? ? 剛開始的時候，對于視頻瀏覽次數的統計是通過讀取?Segment 1?和?Segment 2?來完成的，在?Compaction?完成了之后，對于結果的讀取就可以從?Compacted Segment?里面讀取了。因為這時候所有的結果已經存放在?Compacted Segment?里面了，所以就可以刪除?Segment 1?和?Segment 2?來騰出內存空間了。 整個?Compaction?的過程會不斷地遞歸進行下去，當?Compacted Segment?滿了以后，后臺線程又可以對?Compacted Segment?進行?Compaction?操作，再次合并所有結果。 你會發現，當采用了這種優化之后，寫操作還是可以十分高效地進行下去，同時也不會占用大量的內存空間。 #### SSTable?和?LSM?樹 上面所講到的?Log-Structured?結構的這種?Compaction?優化，其實是?LSM?樹的一個基礎，在學習?LSM?樹之前，我們先來了解一個新的數據結構，即?SSTable。SSTable（Sorted String Table）數據結構是在?Log-Structured?結構的基礎上，多加了一條規則，就是所有保存在?Log-Structured?結構里的數據都是鍵值對，并且鍵必須是字符串，在經過了?Compaction?操作之后，所有的?Compacted Segment?里保存的鍵值對都必須按照字符排序。 我們假設現在想利用?Log-Structured?結構來保存一本書里的詞頻，為了方便說明，把?Segment?的大小設為?4。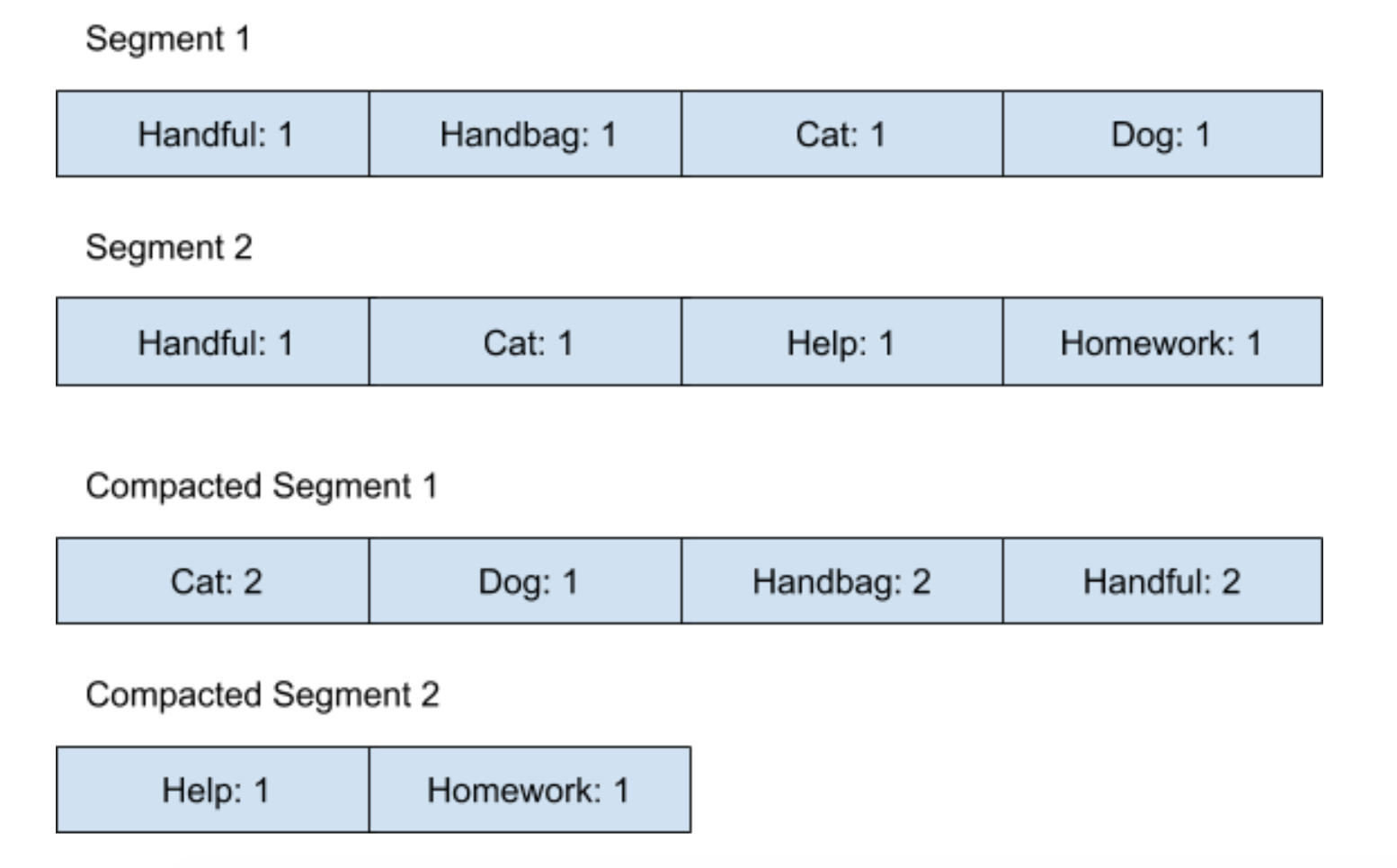在剛開始的時候，這個?Log-Structured?結構的內存圖如下圖所示：  在經過了?Compaction?操作之后，內存圖會變成如下圖所示：  可以看到，所有的?Compacted Segment?都是按照字符串排序的。當我們要查找一個單詞出現的次數時，可以去遍歷所有的?Compacted Segment，來看看這個單詞的詞頻，當然了，因為所有數據都是按照字符串排好序的，如果當遍歷到的字符串已經大于我們要找的字符串時，就表示并沒有出現過這個單詞。 這時候你可能會有一個疑問，Log-Structured?結構是指不停地將新數據加入到?Segment?的結尾，像這種?Compaction?的時候將字符串排序應該怎么做呢？此時我們就需要上一講中所講到的平衡樹了。 我們先來復習一下二叉查找樹里的一個特性：二叉查找樹的任意一個節點都比它的左子樹所有節點大，同時比右子樹所有節點小，說到這里你是不是有點恍然大悟了。如果我們將所有?Log-Structured?結構里的數據都保存在一個二叉查找樹里，當寫入數據時其實是按照任意順序寫入的，而當讀取數據時是按照二叉查找樹的中序遍歷來訪問數據的，其實就相當于按字符串順序讀取了。 在業界上，我們為了維護數據結構讀取的高效，一般都會維護一個平衡樹，比如，在上一講中說到的紅黑樹或者?AVL?樹。而這樣一個平衡樹在?Log-Structured?結構里通常被稱為?memtable。而上面所講到的概念，通過內部維護平衡樹來進行?Log-Structured?結構的?Compaction?優化，這樣一種數據結構被稱為是?LSM?樹（Log-Structured Merge-Tree），它是由?Patrick O'Neil?等人在?1996?年所提出的。 #### LSM?樹的應用 在數據庫里面，有一項功能叫做?Range Query，用于查詢在一個下界和上界之間的數據，比如，查找時間戳在?A?到?B?之內的所有數據。許多著名的數據庫系統，像是?HBase、SQLite?和?MongoDB，它們的底層索引因為采用了?LSM?樹，所以可以很快地定位到一個范圍。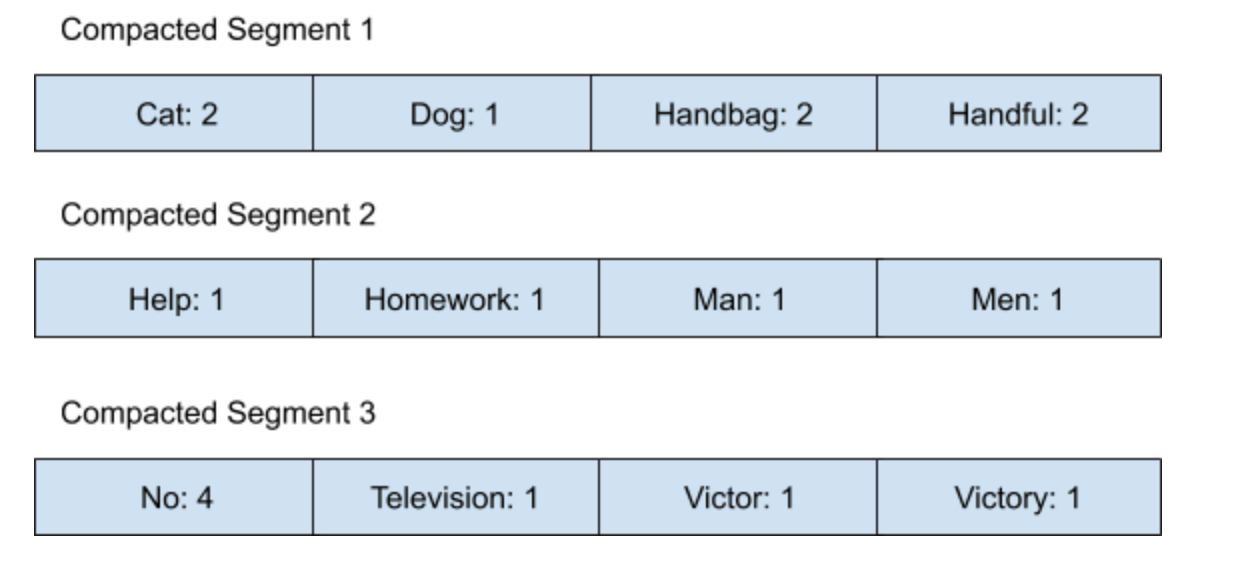 比如，如果內存里保存有以下的?Compacted Segments：  如果我們的查詢是需要找出所有從?Home?到?No?的數據，那我們就知道，可以從?Compacted Segment 2 到 Compacted Segment 3?里面去尋找這些數據了。 同樣的，采用?Lucene?作為后臺索引引擎的開源搜索框架，像?ElasticSearch?和?Solr，底層其實運用了?LSM?樹。因為搜索引擎的特殊性，有可能會遇到一些情況，那就是：所搜索的詞并不在保存的數據里，而想要知道一個數據是否存在?Segment?里面，必須遍歷一次整個?Segment，時間開銷還并不是最優化的，所以這兩個搜索引擎除了采用?LSM?樹之外，還會利用另外一個在第?07?講中所提到的?Bloom Filter?這個數據結構，它可以用來判斷一個詞是否一定不在保存的數據里面。