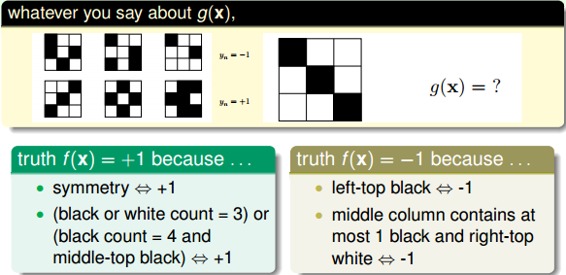
# 4 -- Feasibility of Learning 上節課，我們主要介紹了根據不同的設定，機器學習可以分為不同的類型。其中，監督式學習中的二元分類和回歸分析是最常見的也是最重要的機器學習問題。本節課，我們將介紹機器學習的可行性，討論問題是否可以使用機器學習來解決。 ### **一、Learning is Impossible** 首先，考慮這樣一個例子，如下圖所示，有3個label為-1的九宮格和3個label為+1的九宮格。根據這6個樣本，提取相應label下的特征，預測右邊九宮格是屬于-1還是+1？結果是，如果依據對稱性，我們會把它歸為+1；如果依據九宮格左上角是否是黑色，我們會把它歸為-1。除此之外，還有根據其它不同特征進行分類，得到不同結果的情況。而且，這些分類結果貌似都是正確合理的，因為對于6個訓練樣本來說，我們選擇的模型都有很好的分類效果。  再來看一個比較數學化的二分類例子，輸入特征x是二進制的、三維的，對應有8種輸入，其中訓練樣本D有5個。那么，根據訓練樣本對應的輸出y，假設有8個hypothesis，這8個hypothesis在D上，對5個訓練樣本的分類效果效果都完全正確。但是在另外3個測試數據上，不同的hypothesis表現有好有壞。在已知數據D上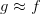，；但是在D以外的未知數據上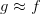，不一定成立。而機器學習目的，恰恰是希望我們選擇的模型能在未知數據上的預測與真實結果是一致的，而不是在已知的數據集D上尋求最佳效果。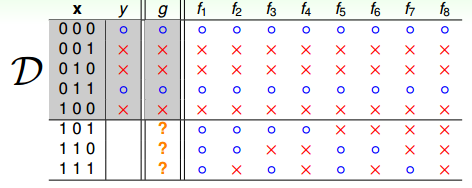  這個例子告訴我們，我們想要在D以外的數據中更接近目標函數似乎是做不到的，只能保證對D有很好的分類結果。機器學習的這種特性被稱為沒有免費午餐（No Free Lunch）定理。NFL定理表明沒有一個學習算法可以在任何領域總是產生最準確的學習器。不管采用何種學習算法，至少存在一個目標函數，能夠使得隨機猜測算法是更好的算法。平常所說的一個學習算法比另一個算法更“優越”，效果更好，只是針對特定的問題，特定的先驗信息，數據的分布，訓練樣本的數目，代價或獎勵函數等。從這個例子來看，NFL說明了無法保證一個機器學習算法在D以外的數據集上一定能分類或預測正確，除非加上一些假設條件，我們以后會介紹。 ### **二、Probability to the Rescue** 從上一節得出的結論是：在訓練集D以外的樣本上，機器學習的模型是很難，似乎做不到正確預測或分類的。那是否有一些工具或者方法能夠對未知的目標函數f做一些推論，讓我們的機器學習模型能夠變得有用呢？ 如果有一個裝有很多（數量很大數不過來）橙色球和綠色球的罐子，我們能不能推斷橙色球的比例u？統計學上的做法是，從罐子中隨機取出N個球，作為樣本，計算這N個球中橙色球的比例v，那么就估計出罐子中橙色球的比例約為v。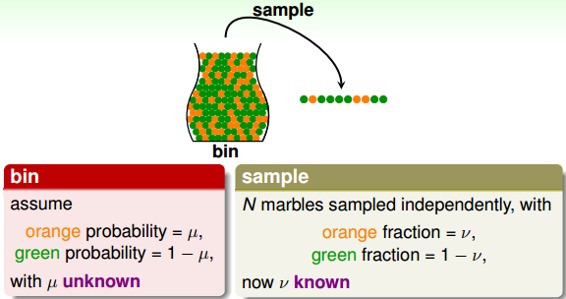  這種隨機抽取的做法能否說明罐子里橙色球的比例一定是v呢？答案是否定的。但是從概率的角度來說，樣本中的v很有可能接近我們未知的u。下面從數學推導的角度來看v與u是否相近。 已知u是罐子里橙色球的比例，v是N個抽取的樣本中橙色球的比例。當N足夠大的時候，v接近于u。這就是Hoeffding’s inequality： Hoeffding不等式說明當N很大的時候，v與u相差不會很大，它們之間的差值被限定在之內。我們把結論v=u稱為probably approximately correct(PAC)。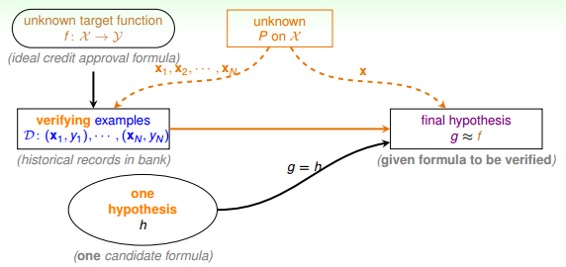  ### **三、Connection to Learning** 下面，我們將罐子的內容對應到機器學習的概念上來。機器學習中hypothesis與目標函數相等的可能性，類比于罐子中橙色球的概率問題；罐子里的一顆顆彈珠類比于機器學習樣本空間的x；橙色的彈珠類比于h(x)與f不相等；綠色的彈珠類比于h(x)與f相等；從罐子中抽取的N個球類比于機器學習的訓練樣本D，且這兩種抽樣的樣本與總體樣本之間都是獨立同分布的。所以呢，如果樣本N夠大，且是獨立同分布的，那么，從樣本中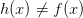的概率就能推導在抽樣樣本外的所有樣本中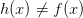的概率是多少。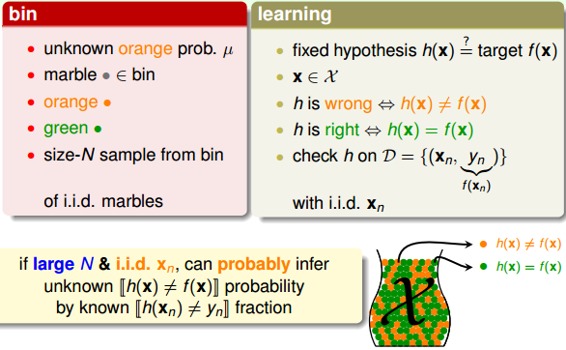  映射中最關鍵的點是講抽樣中橙球的概率理解為樣本數據集D上h(x)錯誤的概率，以此推算出在所有數據上h(x)錯誤的概率，這也是機器學習能夠工作的本質，即我們為啥在采樣數據上得到了一個假設，就可以推到全局呢？因為兩者的錯誤率是PAC的，只要我們保證前者小，后者也就小了。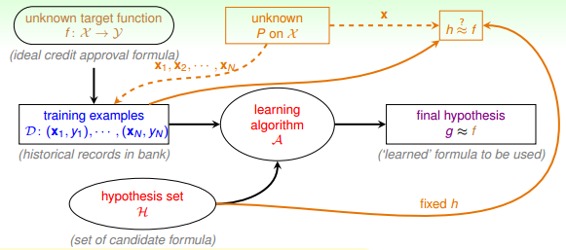  這里我們引入兩個值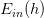和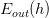。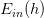表示在抽樣樣本中，h(x)與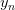不相等的概率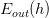；表示實際所有樣本中，h(x)與f(x)不相等的概率是多少。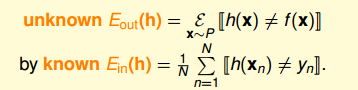  同樣，它的Hoeffding’s inequality可以表示為： 該不等式表明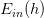，也是PAC的。如果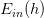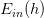，很小，那么就能推斷出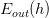很小，也就是說在該數據分布P下，h與f非常接近，機器學習的模型比較準確。 一般地，h如果是固定的，N很大的時候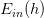，，但是并不意味著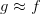。因為h是固定的，不能保證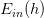足夠小，即使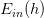，也可能使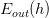偏大。所以，一般會通過演算法A，選擇最好的h，使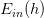足夠小，從而保證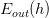很小。固定的h，使用新數據進行測試，驗證其錯誤率是多少。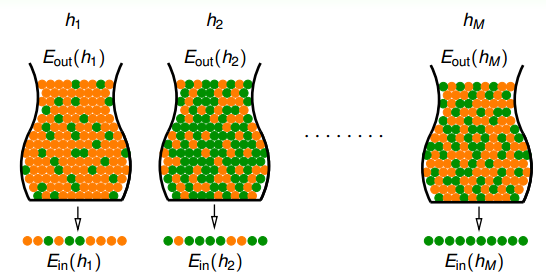  ### **四、Connection to Real Learning**  假設現在有很多罐子M個（即有M個hypothesis），如果其中某個罐子抽樣的球全是綠色，那是不是應該選擇這個罐子呢？我們先來看這樣一個例子：150個人拋硬幣，那么其中至少有一個人連續5次硬幣都是正面朝上的概率是 可見這個概率是很大的，但是能否說明5次正面朝上的這個硬幣具有代表性呢？答案是否定的！并不能說明該硬幣單次正面朝上的概率很大，其實都是0.5。一樣的道理，抽到全是綠色求的時候也不能一定說明那個罐子就全是綠色球。當罐子數目很多或者拋硬幣的人數很多的時候，可能引發Bad Sample，Bad Sample就是和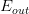差別很大，即選擇過多帶來的負面影響，選擇過多會惡化不好的情形。 根據許多次抽樣的到的不同的數據集D，Hoeffding’s inequality保證了大多數的D都是比較好的情形（即對于某個h，保證），但是也有可能出現Bad Data，即和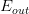差別很大的數據集D，這是小概率事件。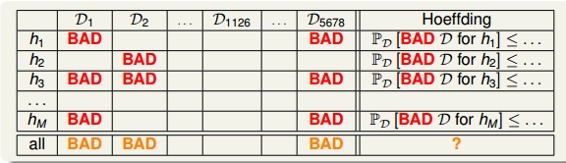  也就是說，不同的數據集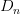，對于不同的hypothesis，有可能成為Bad Data。只要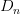在某個hypothesis上是Bad Data，那么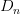就是Bad Data。只有當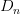在所有的hypothesis上都是好的數據，才說明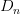不是Bad Data，可以自由選擇演算法A進行建模。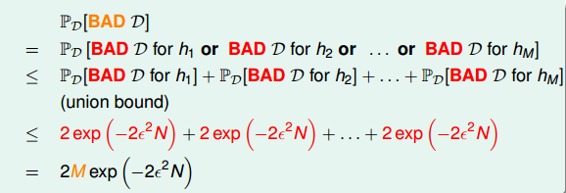那么，根據Hoeffding’s inequality，Bad Data的上界可以表示為連級（union bound）的形式：  其中，M是hypothesis的個數，N是樣本D的數量，是參數。該union bound表明，當M有限，且N足夠大的時候，Bad Data出現的概率就更低了，即能保證D對于所有的h都有，滿足PAC，演算法A的選擇不受限制。那么滿足這種union bound的情況，我們就可以和之前一樣，選取一個合理的演算法（PLA/pocket），選擇使最小的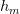作為矩g，一般能夠保證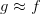，即有不錯的泛化能力。 所以，如果hypothesis的個數M是有限的，N足夠大，那么通過演算法A任意選擇一個矩g，都有成立；同時，如果找到一個矩g，使，PAC就能保證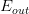。至此，就證明了機器學習是可行的。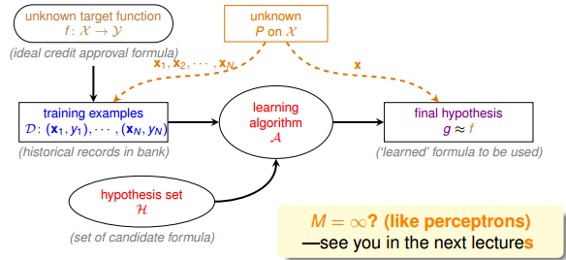  但是，如上面的學習流程圖右下角所示，如果M是無數個，例如之前介紹的PLA直線有無數條，是否這些推論就不成立了呢？是否機器就不能進行學習呢？這些內容和問題，我們下節課再介紹。 ### **五、總結** 本節課主要介紹了機器學習的可行性。首先引入NFL定理，說明機器學習無法找到一個矩g能夠完全和目標函數f一樣。接著介紹了可以采用一些統計上的假設，例如Hoeffding不等式，建立和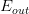的聯系，證明對于某個h，當N足夠大的時候，和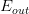是PAC的。最后，對于h個數很多的情況，只要有h個數M是有限的，且N足夠大，就能保證，證明機器學習是可行的。 **_注明：_** 文章中所有的圖片均來自臺灣大學林軒田《機器學習基石》課程。