# 7 -- Blending and Bagging 上節課我們主要介紹了Support Vector Regression，將kernel model引入到regression中。首先，通過將ridge regression和representer theorem結合起來，得到kernel ridge regression。但是其解是dense的，即不部分不為零。為了得到sparse解，我們將regularized tube error和Lagrange dual結合起來，利用SVM dual的推導方法，得到support vector regression的sparse解。本系列1-6節課主要介紹Kernel Models及其應用，從本節課開始，講介紹Aggregation Models，即如何將不同的hypothesis和features結合起來，讓模型更好。本節課將介紹其中的兩個方法，一個是Blending，一個是Bagging。 ### **Motivation of Aggregation** 首先舉個例子來說明為什么要使用Aggregation。假如你有T個朋友，每個朋友向你預測推薦明天某支股票會漲還是會跌，對應的建議分別是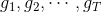，那么你該選擇哪個朋友的建議呢？即最終選擇對股票預測的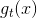是什么樣的？ 第一種方法是從T個朋友中選擇一個最受信任，對股票預測能力最強的人，直接聽從他的建議就好。這是一種普遍的做法，對應的就是validation思想，即選擇犯錯誤最小的模型。第二種方法，如果每個朋友在股票預測方面都是比較厲害的，都有各自的專長，那么就同時考慮T個朋友的建議，將所有結果做個投票，一人一票，最終決定出對該支股票的預測。這種方法對應的是uniformly思想。第三種方法，如果每個朋友水平不一，有的比較厲害，投票比重應該更大一些，有的比較差，投票比重應該更小一些。那么，仍然對T個朋友進行投票，只是每個人的投票權重不同。這種方法對應的是non-uniformly的思想。第四種方法與第三種方法類似，但是權重不是固定的，根據不同的條件，給予不同的權重。比如如果是傳統行業的股票，那么給這方面比較厲害的朋友較高的投票權重，如果是服務行業，那么就給這方面比較厲害的朋友較高的投票權重。以上所述的這四種方法都是將不同人不同意見融合起來的方式，接下來我們就要討論如何將這些做法對應到機器學習中去。Aggregation的思想與這個例子是類似的，即把多個hypothesis結合起來，得到更好的預測效果。  將剛剛舉的例子的各種方法用數學化的語言和機器學習符號歸納表示出來，其中G(x)表示最終選擇的模型。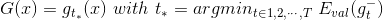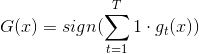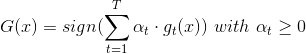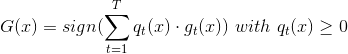 第一種方法對應的模型：  第二種方法對應的模型：  第三種方法對應的模型：  第四種方法對應的模型：   注意這里提到的第一種方法是通過驗證集來選擇最佳模型，不能使用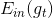來代替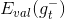。經過Validation，選擇最小的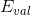，保證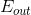最小，從而將對應的模型作為最佳的選擇。 但是第一種方法只是從眾多可能的hypothesis中選擇最好的模型，并不能發揮集體的智慧。而Aggregation的思想是博采眾長，將可能的hypothesis優勢集合起來，將集體智慧融合起來，使預測模型達到更好的效果。 下面先來看一個例子，通過這個例子說明為什么Aggregation能work得更好。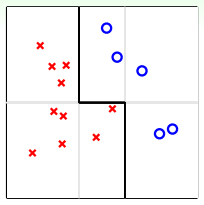  如上圖所示，平面上分布著一些待分類的點。如果要求只能用一條水平的線或者垂直的線進行分類，那不論怎么選取直線，都達不到最佳的分類效果。這實際上就是上面介紹的第一種方法：validation。但是，如果可以使用集體智慧，比如一條水平線和兩條垂直線組合而成的圖中折線形式，就可以將所有的點完全分開，得到了最優化的預測模型。 這個例子表明，通過將不同的hypotheses均勻地結合起來，得到了比單一hypothesis更好的預測模型。這就是aggregation的優勢所在，它提高了預測模型的power，起到了特征轉換（feature transform）的效果。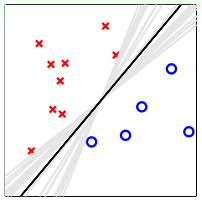  我們再從另外一方面來看，同樣是平面上分布著一些待分類的點，使用PLA算法，可以得到很多滿足條件的分類線，如下圖所示：  這無數條PLA選擇出來的直線對應的hypothesis都是滿足分類要求的。但是我們最想得到的分類直線是中間那條距離所有點都比較遠的黑色直線，這與之前SVM目標是一致的。如果我們將所有可能的hypothesis結合起來，以投票的方式進行組合選擇，最終會發現投票得到的分類線就是中間和黑色那條。這從哲學的角度來說，就是對各種效果較好的可能性進行組合，得到的結果一般是中庸的、最合適的，即對應圖中那條黑色直線。所以，aggregation也起到了正則化（regularization）的效果，讓預測模型更具有代表性。  基于以上的兩個例子，我們得到了aggregation的兩個優勢：feature transform和regularization。我們之前在機器學習基石課程中就介紹過，feature transform和regularization是對立的，還把它們分別比作踩油門和踩剎車。如果進行feature transform，那么regularization的效果通常很差，反之亦然。也就是說，單一模型通常只能傾向于feature transform和regularization之一，在兩者之間做個權衡。但是aggregation卻能將feature transform和regularization各自的優勢結合起來，好比把油門和剎車都控制得很好，從而得到不錯的預測模型。 ### **Uniform Blending** 那對于我們已經選擇的性能較好的一些矩，如何將它們進行整合、合并，來得到最佳的預測模型呢？這個過程稱為blending。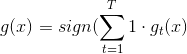 最常用的一種方法是uniform blending，應用于classification分類問題，做法是將每一個可能的矩賦予權重1，進行投票，得到的G(x)表示為：  這種方法對應三種情況：第一種情況是每個候選的矩都完全一樣，這跟選其中任意一個效果相同；第二種情況是每個候選的矩都有一些差別，這是最常遇到的，大都可以通過投票的形式使多數意見修正少數意見，從而得到很好的模型，如下圖所示；第三種情況是多分類問題，選擇投票數最多的那一類即可。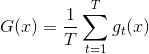  如果是regression回歸問題，uniform blending的做法很簡單，就是將所有的矩求平均值：  uniform blending for regression對應兩種情況：第一種情況是每個候選的矩都完全一樣，這跟選其中任意一個效果相同；第二種情況是每個候選的矩都有一些差別，有的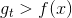，有的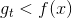，此時求平均值的操作可能會消去這種大于和小于的影響，從而得到更好的回歸模型。因此，從直覺上來說，求平均值的操作更加穩定，更加準確。  對于uniform blending，一般要求每個候選的矩都有一些差別。這樣，通過不同矩的組合和集體智慧，都能得到比單一矩更好的模型。 剛才我們提到了uniform blending for regression中，計算的平均值可能比單一的更穩定，更準確。下面進行簡單的推導和證明。  推導過程中注意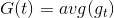。經過推導，我們發現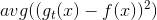與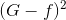之間差了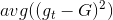項，且是大于零的。從而得到與目標函數f的差值要比G與f的差值大。 剛才是對單一的x進行證明，如果從期望角度，對整個x分布進行上述公式的整理，得到：  從結果上來看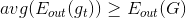，，從而證明了從平均上來說，計算的平均值G(t)要比單一的更接近目標函數f，regression效果更好。 我們已經知道G是數目為T的的平均值。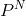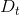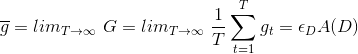令包含N個數據的樣本D獨立同分布于，每次從新的中學習得到新的，在對求平均得到G，當做無限多次，即T趨向于無窮大的時候：   當T趨于無窮大的時候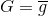，，則有如下等式成立：  上述等式中左邊表示演算法誤差的期望值；右邊第二項表示不同的平均誤差共識，用偏差bias表示；右邊第一項表示不同與共識的差距是多少，反映之間的偏差，用方差variance表示。也就是說，一個演算法的平均表現可以被拆成兩項，一個是所有的共識，一個是不同之間的差距是多少，即bias和variance。而uniform blending的操作時求平均的過程，這樣就削減弱化了上式第一項variance的值，從而演算法的表現就更好了，能得到更加穩定的表現。 ### **Linear and Any Blending** 上一部分講的是uniform blending，即每個所占的權重都是1，求平均的思想。下面我們將介紹linear blending，每個賦予的權重并不相同，其中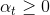。我們最終得到的預測結果等于所有的線性組合。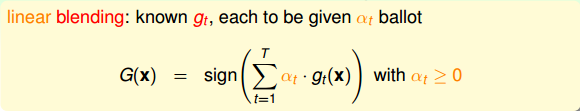  如何確定的值，方法是利用誤差最小化的思想，找出最佳的，使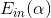取最小值。例如對于linear blending for regression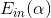，可以寫成下圖左邊形式，其中是帶求解參數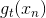，是每個矩得到的預測值，由已知矩得到。這種形式很類似于下圖右邊的形式，即加上特征轉換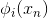的linear regression模型。兩個式子中的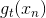對應于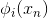，唯一不同的就是linear blending for regression中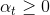，而linear regression中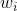沒有限制。  這種求解的方法就像是使用two-level learning，類似于我們之前介紹的probabilistic SVM。這里，我們先計算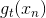，再進行linear regression得到值。總的來說，linear blending由三個部分組成：LinModel，hypotheses as transform，constraints。其中值得注意的一點就是，計算過程中可以把當成feature transform，求解過程就跟之前沒有什么不同，除了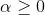的條件限制。  我們來看一下linear blending中的constraint 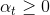。這個條件是否一定要成立呢？如果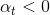，會帶來什么后果呢？其實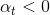并不會影響分類效果，只需要將正類看成負類，負類當成正類即可。例如分類問題，判斷該點是正類對應的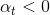，則它就表示該點是負類，且對應的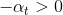。如果我們說這個樣本是正類的概率是-99%，意思也就是說該樣本是負類的概率是99%。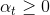和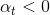的效果是等同的一致的。所以，我們可以把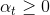這個條件舍去，這樣linear blending就可以使用常規方法求解。  Linear Blending中使用的是通過模型選擇而得到的，利用validation，從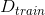中得到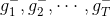。然后將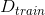中每個數據點經過各個矩的計算得到的值，代入到相應的linear blending計算公式中，迭代優化得到對應值。最終，再利用所有樣本數據，得到新的代替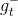，則G(t)就是的線性組合而不是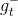，系數是。   除了linear blending之外，還可以使用任意形式的blending。linear blending中，G(t)是g(t)的線性組合；any blending中，G(t)可以是g(t)的任何函數形式（非線性）。這種形式的blending也叫做Stacking。any blending的優點是模型復雜度提高，更容易獲得更好的預測模型；缺點是復雜模型也容易帶來過擬合的危險。所以，在使用any blending的過程中要時刻注意避免過擬合發生，通過采用regularization的方法，讓模型具有更好的泛化能力。 ### **Bagging(Bootstrap Aggregation)** 總結一些上面講的內容，blending的做法就是將已經得到的矩進行aggregate的操作。具體的aggregation形式包括：uniform，non-uniforn和conditional。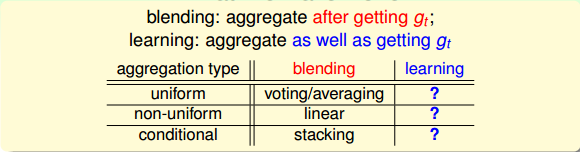  現在考慮一個問題：如何得到不同的呢？可以選取不同模型H；可以設置不同的參數，例如、迭代次數n等；可以由算法的隨機性得到，例如PLA、隨機種子等；可以選擇不同的數據樣本等。這些方法都可能得到不同的。  那如何利用已有的一份數據集來構造出不同的呢？首先，我們回顧一下之前介紹的bias-variance，即一個演算法的平均表現可以被拆成兩項，一個是所有的共識（bias），一個是不同之間的差距是多少（variance）。其中每個都是需要新的數據集的。只有一份數據集的情況下，如何構造新的數據集？  其中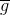，是在矩個數T趨向于無窮大的時候，不同的計算平均得到的值。這里我們為了得到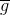，做兩個近似條件： * **有限的T；** * **由已有數據集D構造出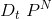，獨立同分布** 第一個條件沒有問題，第二個近似條件的做法就是bootstrapping。bootstrapping是統計學的一個工具，思想就是從已有數據集D中模擬出其他類似的樣本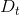。  bootstrapping的做法是，假設有N筆資料，先從中選出一個樣本，再放回去，再選擇一個樣本，再放回去，共重復N次。這樣我們就得到了一個新的N筆資料，這個新的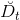中可能包含原D里的重復樣本點，也可能沒有原D里的某些樣本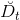，與D類似但又不完全相同。值得一提的是，抽取-放回的操作不一定非要是N，次數可以任意設定。例如原始樣本有10000個，我們可以抽取-放回3000次，得到包含3000個樣本的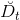也是完全可以的。利用bootstrap進行aggragation的操作就被稱為bagging。  下面舉個實際中Bagging Pocket算法的例子。如下圖所示，先通過bootstrapping得到25個不同樣本集，再使用pocket算法得到25個不同的，每個pocket算法迭代1000次。最后，再利用blending，將所有的融合起來，得到最終的分類線，如圖中黑線所示。可以看出，雖然bootstrapping會得到差別很大的分類線（灰線），但是經過blending后，得到的分類線效果是不錯的，則bagging通常能得到最佳的分類模型。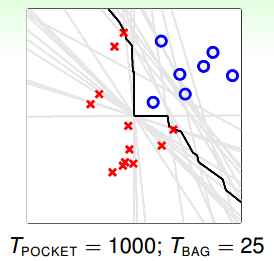  值得注意的是，只有當演算法對數據樣本分布比較敏感的情況下，才有比較好的表現。 ### **總結** 本節課主要介紹了blending和bagging的方法，它們都屬于aggregation，即將不同的合并起來，利用集體的智慧得到更加優化的G(t)。Blending通常分為三種情況：Uniform Blending，Linear Blending和Any Blending。其中，uniform blending采樣最簡單的“一人一票”的方法，linear blending和any blending都采用標準的two-level learning方法，類似于特征轉換的操作，來得到不同的線性組合或非線性組合。最后，我們介紹了如何利用bagging（bootstrap aggregation），從已有數據集D中模擬出其他類似的樣本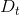，而得到不同的，再合并起來，優化預測模型。 **_注明：_** 文章中所有的圖片均來自臺灣大學林軒田《機器學習技法》課程