# 16 -- Three Learning Principles 上節課我們講了一個機器學習很重要的工具——Validation。我們將整個訓練集分成兩部分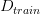：和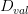，一部分作為機器學習模型建立的訓練數據，另一部分作為驗證模型好壞的數據，從而選擇到更好的模型，實現更好的泛化能力。這節課，我們主要介紹機器學習中非常實用的三個“錦囊妙計”。 ### **一、Occam’s Razor** 奧卡姆剃刀定律（Occam’s Razor），是由14世紀邏輯學家、圣方濟各會修士奧卡姆的威廉（William of Occam，約1285年至1349年）提出。奧卡姆（Ockham）在英格蘭的薩里郡，那是他出生的地方。他在《箴言書注》2卷15題說“切勿浪費較多東西去做用較少的東西同樣可以做好的事情。” 這個原理稱為“如無必要，勿增實體”（Entities must not be multiplied unnecessarily），就像剃刀一樣，將不必要的部分去除掉。 Occam’s Razor反映到機器學習領域中，指的是在所有可能選擇的模型中，我們應該選擇能夠很好地解釋已知數據并且十分簡單的模型。  上圖就是一個模型選擇的例子，左邊的模型很簡單，可能有分錯的情況；而右邊的模型非常復雜，所有的訓練樣本都分類正確。但是，我們會選擇左邊的模型，它更簡單，符合人類直覺的解釋方式。這樣的結果帶來兩個問題：一個是什么模型稱得上是簡單的？另一個是為什么簡單模型比復雜模型要好？ 簡單的模型一方面指的是簡單的hypothesis h，簡單的hypothesis就是指模型使用的特征比較少，例如多項式階數比較少。簡單模型另一方面指的是模型H包含的hypothesis數目有限，不會太多，這也是簡單模型包含的內容。  其實，simple hypothesis h和simple model H是緊密聯系的。如果hypothesis的特征個數是l，那么H中包含的hypothesis個數就是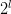，也就是說，hypothesis特征數目越少，H中hypothesis數目也就越少。 所以，為了讓模型簡單化，我們可以一開始就選擇簡單的model，或者用regularization，讓hypothesis中參數個數減少，都能降低模型復雜度。 那為什么簡單的模型更好呢？下面從哲學的角度簡單解釋一下。機器學習的目的是“找規律”，即分析數據的特征，總結出規律性的東西出來。假設現在有一堆沒有規律的雜亂的數據需要分類，要找到一個模型，讓它的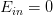，是很難的，大部分時候都無法正確分類，但是如果是很復雜的模型，也有可能將其分開。反過來說，如果有另一組數據，如果可以比較容易找到一個模型能完美地把數據分開，那表明數據本身應該是有某種規律性。也就是說雜亂的數據應該不可以分開，能夠分開的數據應該不是雜亂的。如果使用某種簡單的模型就可以將數據分開，那表明數據本身應該符合某種規律性。相反地，如果用很復雜的模型將數據分開，并不能保證數據本身有規律性存在，也有可能是雜亂的數據，因為無論是有規律數據還是雜亂數據，復雜模型都能分開。這就不是機器學習模型解決的內容了。所以，模型選擇中，我們應該盡量先選擇簡單模型，例如最簡單的線性模型。 ### **二、Sampling Bias** 首先引入一個有趣的例子：1948年美國總統大選的兩位熱門候選人是Truman和Dewey。一家報紙通過電話采訪，統計人們把選票投給了Truman還是Dewey。經過大量的電話統計顯示，投給Dewey的票數要比投個Truman的票數多，所以這家報紙就在選舉結果還沒公布之前，信心滿滿地發表了“Dewey Defeats Truman”的報紙頭版，認為Dewey肯定贏了。但是大選結果公布后，讓這家報紙大跌眼鏡，最終Truman贏的了大選的勝利。 為什么會出現跟電話統計完全相反的結果呢？是因為電話統計數據出錯還是投票運氣不好？都不是。其實是因為當時電話比較貴，有電話的家庭比較少，而正好是有電話的美國人支持Dewey的比較多，而沒有電話的支持Truman比較多。也就是說樣本選擇偏向于有錢人那邊，可能不具有廣泛的代表性，才造成Dewey支持率更多的假象。 這個例子表明，抽樣的樣本會影響到結果，用一句話表示“If the data is sampled in a biased way, learning will produce a similarly biased outcome.”意思是，如果抽樣有偏差的話，那么學習的結果也產生了偏差，這種情形稱之為抽樣偏差Sampling Bias。 從技術上來說，就是訓練數據和驗證數據要服從同一個分布，最好都是獨立同分布的，這樣訓練得到的模型才能更好地具有代表性。 ### **三、Data Snooping** 之前的課程，我們介紹過在模型選擇時應該盡量避免偷窺數據，因為這樣會使我們人為地傾向于某種模型，而不是根據數據進行隨機選擇。所以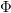，應該自由選取，最好不要偷窺到原始數據，這會影響我們的判斷。 事實上，數據偷窺發生的情況有很多，不僅僅指我們看到了原始數據。什么意思呢？其實，當你在使用這些數據的任何過程，都是間接地偷看到了數據本身，然后你會進行一些模型的選擇或者決策，這就增加了許多的model complexity，也就是引入了污染。 下面舉個例子來說明。假如我們有8年的貨比交易數據，我們希望從這些數據中找出規律，來預測貨比的走勢。如果選擇前6年數據作為訓練數據，后2年數據作為測試數據的話，來訓練模型。現在我們有前20天的數據，根據之前訓練的模型，來預測第21天的貨比交易走勢。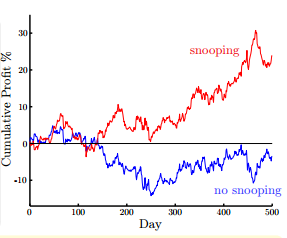  現在有兩種訓練模型的方法，如圖所示，一種是使用前6年數據進行模型訓練，后2年數據作為測試，圖中藍色曲線表示后2年的預測收益；另一種是直接使用8年數據進行模型訓練，圖中紅色曲線表示后2年的預測收益情況。圖中，很明顯，使用8年數據進行訓練的模型對后2年的預測的收益更大，似乎效果更好。但是這是一種自欺欺人的做法，因為訓練的時候已經拿到了后2年的數據，用這樣的模型再來預測后2年的走勢是不科學的。這種做法也屬于間接偷窺數據的行為。直接偷窺和間接偷窺數據的行為都是不科學的做法，并不能表示訓練的模型有多好。  還有一個偷窺數據的例子，比如對于某個基準數據集D，某人對它建立了一個模型H1，并發表了論文。第二個人看到這篇論文后，又會對D，建立一個新的好的模型H2。這樣，不斷地有人看過前人的論文后，建立新的模型。其實，后面人選擇模型時，已經被前人影響了，這也是偷窺數據的一種情況。也許你能對D訓練很好的模型，但是可能你僅僅只根據前人的模型，成功避開了一些錯誤，甚至可能發生了overfitting或者bad generalization。所以，機器學習領域有這樣一句有意思的話“If you torture the data long enough, it will confess.”所以，我們不能太“折磨”我們的數據了，否則它只能“妥協”了~哈哈。 在機器學習過程中，避免“偷窺數據”非常重要，但實際上，完全避免也很困難。實際操作中，有一些方法可以幫助我們盡量避免偷窺數據。第一個方法是“看不見”數據。就是說當我們在選擇模型的時候，盡量用我們的經驗和知識來做判斷選擇，而不是通過數據來選擇。先選模型，再看數據。第二個方法是保持懷疑。就是說時刻保持對別人的論文或者研究成果保持警惕與懷疑，要通過自己的研究與測試來進行模型選擇，這樣才能得到比較正確的結論。  ### **四、Power of Three** 本小節，我們對16節課做個簡單的總結，用“三的威力”進行概括。因為課程中我們介紹的很多東西都與三有關。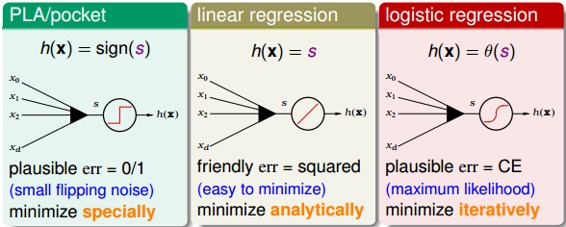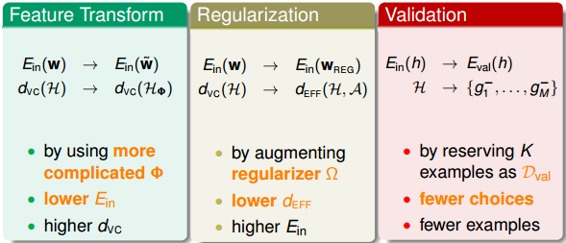 首先，我們介紹了跟機器學習相關的三個領域： * Data Mining * Artificial Intelligence * Statistics  我們還介紹了三個理論保證： * Hoeffding * Multi-Bin Hoeffding * VC  然后，我們又介紹了三種線性模型： * PLA/pocket * linear regression * logistic regression  同時，我們介紹了三種重要的工具： * Feature Transform * Regularization * Validation  還有我們本節課介紹的三個錦囊妙計： * Occam’s Razer * Sampling Bias * Data Snooping  最后，我們未來機器學習的方向也分為三種： * More Transform * More Regularization * Less Label  ### **五、總結** 本節課主要介紹了機器學習三個重要的錦囊妙計：Occam’s Razor, Sampling Bias, Data Snooping。并對《機器學習基石》課程中介紹的所有知識和方法進行“三的威力”這種形式的概括與總結，“三的威力”也就構成了堅固的機器學習基石。 整個機器學習基石的課程筆記總結完畢！后續將會推出機器學習技法的學習筆記，謝謝！ **_注明：_** 文章中所有的圖片均來自臺灣大學林軒田《機器學習基石》課程