# 9 -- Decision Tree 上節課我們主要介紹了Adaptive Boosting。AdaBoost演算法通過調整每筆資料的權重，得到不同的hypotheses，然后將不同的hypothesis乘以不同的系數進行線性組合。這種演算法的優點是，即使底層的演算法g不是特別好（只要比亂選好點），經過多次迭代后算法模型會越來越好，起到了boost提升的效果。本節課將在此基礎上介紹一種新的aggregation算法：決策樹（Decision Tree）。 ### **Decision Tree Hypothesis** 從第7節課開始，我們就一直在介紹aggregation model。aggregation的核心就是將許多可供選擇使用的比較好的hypothesis融合起來，利用集體的智慧組合成G，使其得到更好的機器學習預測模型。下面，我們先來看看已經介紹過的aggregation type有哪些。  aggregation type有三種：uniform，non-uniform，conditional。它有兩種情況，一種是所有的g是已知的，即blending。對應的三種類型分別是voting/averaging，linear和stacking。另外一種情況是所有g未知，只能通過手上的資料重構g，即learning。其中uniform和non-uniform分別對應的是Bagging和AdaBoost算法，而conditional對應的就是我們本節課將要介紹的Decision Tree算法。 決策樹（Decision Tree）模型是一種傳統的算法，它的處理方式與人類思維十分相似。例如下面這個例子，對下班時間、約會情況、提交截止時間這些條件進行判斷，從而決定是否要進行在線課程測試。如下圖所示，整個流程類似一個樹狀結構。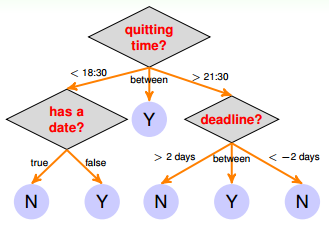  圖中每個條件和選擇都決定了最終的結果，Y or N。藍色的圓圈表示樹的葉子，即最終的決定。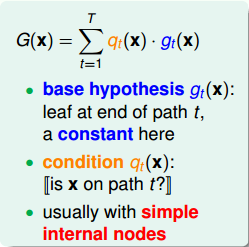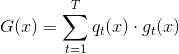 把這種樹狀結構對應到一個hypothesis G(x)中，G(x)的表達式為：  G(x)由許多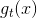組成，即aggregation的做法。每個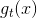就代表上圖中的藍色圓圈（樹的葉子）。這里的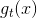是常數，因為是處理簡單的classification問題。我們把這些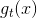稱為base hypothesis。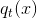表示每個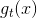成立的條件，代表上圖中橘色箭頭的部分。不同的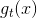對應于不同的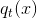，即從樹的根部到頂端葉子的路徑不同。圖中中的菱形代表每個簡單的節點。所以，這些base hypothesis和conditions就構成了整個G(x)的形式，就像一棵樹一樣，從根部到頂端所有的葉子都安全映射到上述公式上去了。  決策樹實際上就是在模仿人類做決策的過程。一直以來，決策樹的應用十分廣泛而且分類預測效果都很不錯，而它在數學上的理論完備性不充分，倒也不必在意。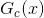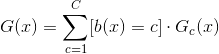 如果從另外一個方面來看決策樹的形式，不同于上述G(x)的公式，我們可以利用條件分支的思想，將整體G(x)分成若干個，也就是把整個大樹分成若干個小樹，如下所示：  上式中，G(x)表示完整的大樹，即full-tree hypothesis，b(x)表示每個分支條件，即branching criteria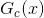，表示第c個分支下的子樹，即sub-tree。這種結構被稱為遞歸型的數據結構，即將大樹分割成不同的小樹，再將小樹繼續分割成更小的子樹。所以，決策樹可以分為兩部分：root和sub-trees。  在詳細推導決策樹算法之前，我們先來看一看它的優點和缺點。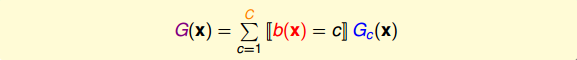首先，decision tree的優點有： * **模型直觀，便于理解，應用廣泛** * **算法簡單，容易實現** * **訓練和預測時，效率較高** 然而，decision tree也有相應的缺點： * **缺少足夠的理論支持** * **如何選擇合適的樹結構對初學者來說比較困惑** * **決策樹代表性的演算法比較少**  ### **Decision Tree Algorithm** 我們可以用遞歸形式將decision tree表示出來，它的基本的算法可以寫成：  這個Basic Decision Tree Algorithm的流程可以分成四個部分，首先學習設定劃分不同分支的標準和條件是什么；接著將整體數據集D根據分支個數C和條件，劃為不同分支下的子集Dc；然后對每個分支下的Dc進行訓練，得到相應的機器學習模型Gc；最后將所有分支下的Gc合并到一起，組成大矩G(x)。但值得注意的是，這種遞歸的形式需要終止條件，否則程序將一直進行下去。當滿足遞歸的終止條件之后，將會返回基本的hypothesis 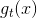。  所以，決策樹的基本演算法包含了四個選擇： * **分支個數（number of branches）** * **分支條件（branching criteria）** * **終止條件（termination criteria）** * **基本算法（base hypothesis）** 下面我們來介紹一種常用的決策樹模型算法，叫做Classification and Regression Tree(C&RT)。C&RT算法有兩個簡單的設定，首先，分支的個數C=2，即二叉樹（binary tree）的數據結構；然后，每個分支最后的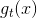（數的葉子）是一個常數。按照最小化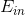的目標，對于binary/multiclass classification(0/1 error)問題，看正類和負類哪個更多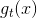，取所占比例最多的那一類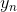；對于regression(squared error)問題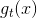，則取所有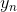的平均值。  對于決策樹的基本演算法流程，C&RT還有一些簡單的設定。首先，C&RT分支個數C=2，一般采用上節課介紹過的decision stump的方法進行數據切割。也就是每次在一個維度上，只對一個特征feature將數據一分為二，左子樹和右子樹，分別代表不同的類別。然而，怎么切割才能讓數據劃分得最好呢（error最小）？C&RT中使用純凈度purifying這個概念來選擇最好的decision stump。purifying的核心思想就是每次切割都盡可能讓左子樹和右子樹中同類樣本占得比例最大或者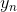都很接近（regression），即錯誤率最小。比如說classifiacation問題中，如果左子樹全是正樣本，右子樹全是負樣本，那么它的純凈度就很大，說明該分支效果很好。  根據C&RT中purifying的思想，我們得到選擇合適的分支條件b(x)的表達式如上所示。最好的decision stump重點包含兩個方面：一個是剛剛介紹的分支純凈度purifying，purifying越大越好，而這里使用purifying相反的概念impurity，則impurity越小越好；另外一個是左右分支純凈度所占的權重，權重大小由該分支的數據量決定，分支包含的樣本個數越多，則所占權重越大，分支包含的樣本個數越少，則所占權重越小。上式中的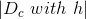代表了分支c所占的權重。這里b(x)類似于error function（這也是為什么使用impurity代替purifying的原因），選擇最好的decision stump，讓所有分支的不純度最小化，使b(x)越小越好。 不純度Impurity如何用函數的形式量化？一種簡單的方法就是類比于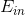，看預測值與真實值的誤差是多少。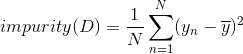對于regression問題，它的impurity可表示為：  其中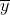，表示對應分支下所有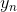的均值。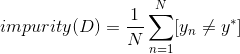 對應classification問題，它的impurity可表示為：  其中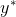，表示對應分支下所占比例最大的那一類。  以上這些impurity是基于原來的regression error和classification error直接推導的。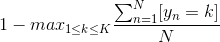進一步來看classification的impurity functions，如果某分支條件下，讓其中一個分支純度最大，那么就選擇對應的decision stump，即得到的classification error為：  其中，K為分支個數。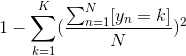 上面這個式子只考慮純度最大的那個分支，更好的做法是將所有分支的純度都考慮并計算在內，用基尼指數（Gini index）表示：  Gini index的優點是將所有的class在數據集中的分布狀況和所占比例全都考慮了，這樣讓decision stump的選擇更加準確。  對于決策樹C&RT算法，通常來說，上面介紹的各種impurity functions中，Gini index更適合求解classification問題，而regression error更適合求解regression問題。 C&RT算法迭代終止條件有兩種情況，第一種情況是當前各個分支下包含的所有樣本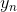都是同類的，即不純度impurity為0，表示該分支已經達到了最佳分類程度。第二種情況是該特征下所有的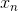相同，無法對其進行區分，表示沒有decision stumps。遇到這兩種情況，C&RT算法就會停止迭代。  所以，C&RT算法遇到迭代終止條件后就成為完全長成樹（fully-grown tree）。它每次分支為二，是二叉樹結構，采用purify來選擇最佳的decision stump來劃分，最終得到的葉子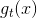（）是常數。 ### **Decision Tree Heuristics in C&RT** 現在我們已經知道了C&RT算法的基本流程：  可以看到C&RT算法在處理binary classification和regression問題時非常簡單實用，而且，處理muti-class classification問題也十分容易。 考慮這樣一個問題，有N個樣本，如果我們每次只取一個樣本點作為分支，那么在經過N-1次分支之后，所有的樣本點都能完全分類正確。最終每片葉子上只有一個樣本，有N片葉子，即必然能保證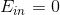。這樣看似是完美的分割，但是不可避免地造成VC Dimension無限大，造成模型復雜度增加，從而出現過擬合現象。為了避免overfit，我們需要在C&RT算法中引入正則化，來控制整個模型的復雜度。 考慮到避免模型過于復雜的方法是減少葉子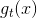（）的數量，那么可以令regularizer就為決策樹中葉子的總數，記為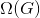。正則化的目的是盡可能減少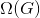的值。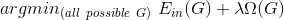這樣，regularized decision tree的形式就可以表示成：  我們把這種regularized decision tree稱為pruned decision tree。pruned是修剪的意思，通過regularization來修剪決策樹，去掉多余的葉子，更簡潔化，從而達到避免過擬合的效果。 那么如何確定修剪多少葉子，修剪哪些葉子呢？假設由C&RT算法得到一棵完全長成樹（fully-grown tree），總共10片葉子。首先分別減去其中一片葉子，剩下9片，將這10種情況比較，取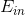最小的那個模型；然后再從9片葉子的模型中分別減去一片，剩下8片，將這9種情況比較，取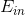最小的那個模型。以此類推，繼續修建葉子。這樣，最終得到包含不同葉子的幾種模型，將這幾個使用regularized decision tree的error function來進行選擇，確定包含幾片葉子的模型誤差最小，就選擇該模型。另外，參數可以通過validation來確定最佳值。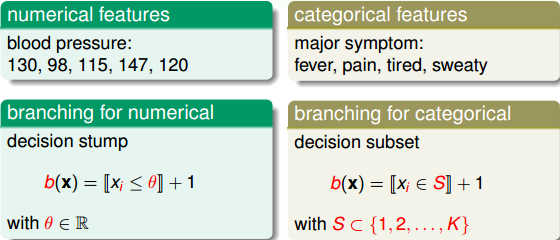  我們一直討論決策樹上的葉子（features）都是numerical features，而實際應用中，決策樹的特征值可能不是數字量，而是類別（categorical features）。對于numerical features，我們直接使用decision stump進行數值切割；而對于categorical features，我們仍然可以使用decision subset，對不同類別進行“左”和“右”，即是與不是（0和1）的劃分。numerical features和categorical features的具體區別如下圖所示：  在決策樹中預測中，還會遇到一種問題，就是當某些特征缺失的時候，沒有辦法進行切割和分支選擇。一種常用的方法就是surrogate branch，即尋找與該特征相似的替代feature。如何確定是相似的feature呢？做法是在決策樹訓練的時候，找出與該特征相似的feature，如果替代的feature與原feature切割的方式和結果是類似的，那么就表明二者是相似的，就把該替代的feature也存儲下來。當預測時遇到原feature缺失的情況，就用替代feature進行分支判斷和選擇。  ### **Decision Tree in Action** 最后我們來舉個例子看看C&RT算法究竟是如何進行計算的。例如下圖二維平面上分布著許多正負樣本，我們使用C&RT算法來對其進行決策樹的分類。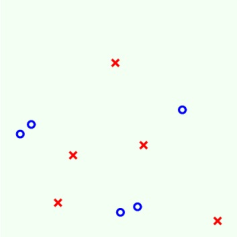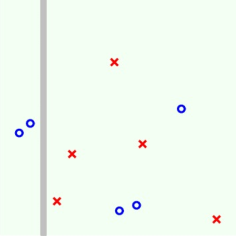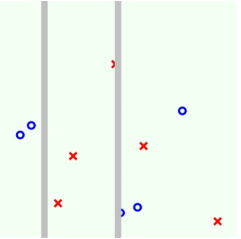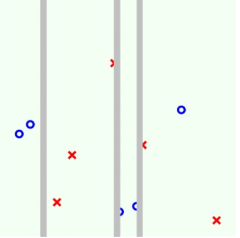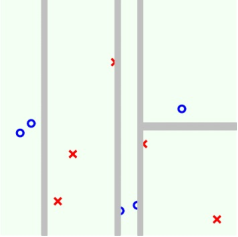  第一步：  第二步：  第三步：  第四步：  在進行第四步切割之后，我們發現每個分支都已經非常純凈了，沒有辦法繼續往下切割。此時表明已經滿足了迭代終止條件，這時候就可以回傳base hypothesis，構成sub tree，然后每個sub tree再往上整合形成tree，最后形成我們需要的完全決策樹。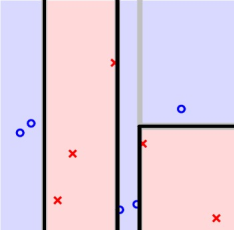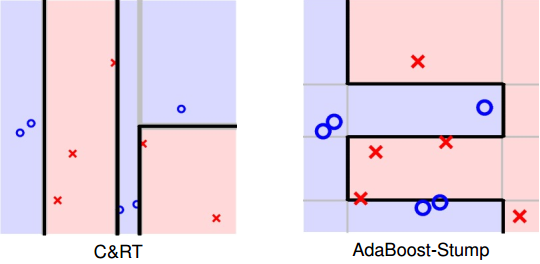如果將邊界添加上去，可得到下圖：  得到C&RT算法的切割方式之后，我們與AdaBoost-Stump算法進行比較：  我們之前就介紹過，AdaBoost-Stump算法的切割線是橫跨整個平面的；而C&RT算法的切割線是基于某個條件的，所以一般不會橫跨整個平面。比較起來，雖然C&RT和AdaBoost-Stump都采用decision stump方式進行切割，但是二者在細節上還是有所區別。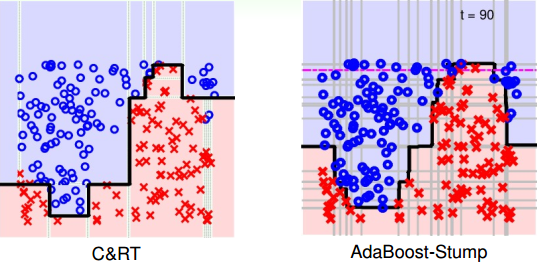 再看一個數據集分布比較復雜的例子，C&RT和AdaBoost-Stump的切割方式對比效果如下圖所示：  通常來說，由于C&RT是基于條件進行切割的，所以C&RT比AdaBoost-Stump分類切割更有效率。總結一下，C&RT決策樹有以下特點：  ### **總結：** 本節課主要介紹了Decision Tree。首先將decision tree hypothesis對應到不同分支下的矩。然后再介紹決策樹算法是如何通過遞歸的形式建立起來。接著詳細研究了決策樹C&RT算法對應的數學模型和算法架構流程。最后通過一個實際的例子來演示決策樹C&RT算法是如何一步一步進行分類的。 **_注明：_** 文章中所有的圖片均來自臺灣大學林軒田《機器學習技法》課程