# 13 -- Deep Learning 上節課我們主要介紹了神經網絡Neural Network。神經網絡是由一層一層的神經元構成，其作用就是幫助提取原始數據中的模式即特征，簡稱為pattern feature extraction。神經網絡模型的關鍵是計算出每個神經元的權重，方法就是使用Backpropagation算法，利用GD/SGD，得到每個權重的最優解。本節課我們將繼續對神經網絡進行深入研究，并介紹層數更多、神經元個數更多、模型更復雜的神經網絡模型，即深度學習模型。 ### **Deep Neural Network** 總的來說，根據神經網絡模型的層數、神經元個數、模型復雜度不同，大致可分為兩類：Shallow Neural Networks和Deep Neural Networks。上節課介紹的神經網絡模型層數較少，屬于Shallow Neural Networks，而本節課將著重介紹Deep Neural Networks。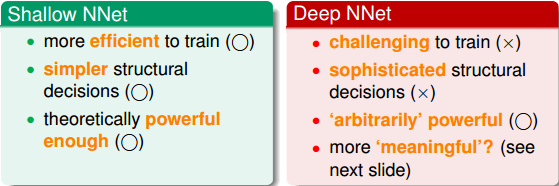首先，比較一下二者之間的優缺點有哪些：  值得一提的是，近些年來，deep learning越來越火，尤其在電腦視覺和語音識別等領域都有非常廣泛的應用。原因在于一層一層的神經網絡有助于提取圖像或者語音的一些物理特征，即pattern feature extraction，從而幫助人們掌握這些問題的本質，建立準確的模型。 下面舉個例子，來看一下深度學習是如何提取出問題潛在的特征從而建立準確的模型的。如下圖所示，這是一個手寫識別的問題，簡單地識別數字1和數字5。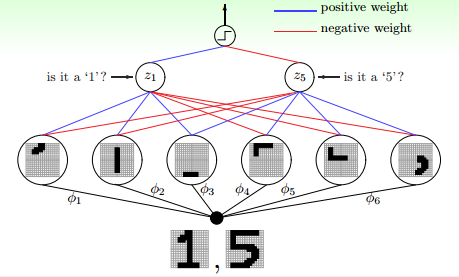  如何進行準確的手寫識別呢？我們可以將寫上數字的圖片分解提取出一塊一塊不同部位的特征。例如左邊三幅圖每張圖代表了數字1的某個部位的特征，三幅圖片組合起來就是完整的數字1。右邊四幅圖也是一樣，每張圖代表了數字5的某個部位的特征，五幅圖組合起來就是完整的數字5。對計算機來說，圖片由許多像素點組成。要達到識別的目的，每層神經網絡從原始像素中提取出更復雜的特征，再由這些特征對圖片內容進行匹配和識別。層數越多，提取特征的個數和深度就越大，同時解決復雜問題的能量就越強，其中每一層都具有相應的物理意義。以上就是深度學習的作用和意義。 深度學習很強大，同時它也面臨很多挑戰和困難： * **difficult structural decisions** * **high model complexity** * **hard optimization problem** * **huge computational complexity** 面對以上深度學習的4個困難，有相應的技術和解決的辦法：  其中，最關鍵的技術就是regularization和initialization。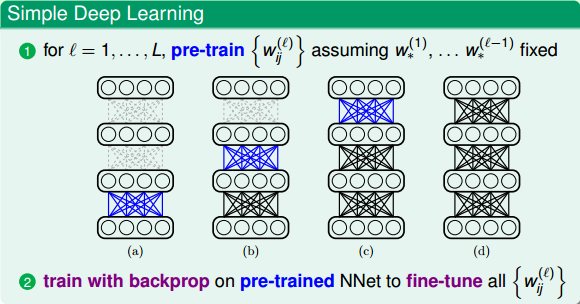 深度學習中，權重的初始化選擇很重要，好的初始值能夠幫助避免出現局部最優解的出現。常用的方法就是pre-train，即先權重進行初始值的選擇，選擇之后再使用backprop算法訓練模型，得到最佳的權重值。在接下來的部分，我們將重點研究pre-training的方法。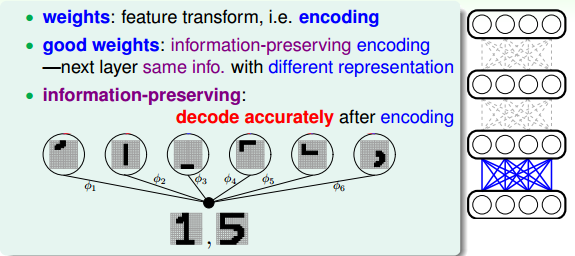  ### **Autoencoder** 我們已經介紹了深度學習的架構，那么從算法模型上來說，如何進行pre-training，得到較好的權重初始值呢？首先，我們來看看，權重是什么？神經網絡模型中，權重代表了特征轉換（feature transform）。從另一個方面也可以說，權重表示一種編碼（encoding），就是把數據編碼成另外一些數據來表示。因為神經網絡是一層一層進行的，有先后順序，所以就單一層來看，好的權重初始值應該是盡可能地包含了該層輸入數據的所有特征，即類似于information-preserving encoding。也就是說，能夠把第i層的輸入數據的特征傳輸到第i+1層，再把第i+1層的輸入數據的特征傳輸到第i+2層，一層一層進行下去。這樣，每層的權重初始值起到了對該層輸入數據的編碼作用，能夠最大限度地保持其特征。 舉個例子，上一小節我們講了簡單的手寫識別的例子。從原始的一張像素圖片轉換到分解的不同筆畫特征，那么反過來，這幾個筆畫特征也可以組合成原來的數字。這種可逆的轉換被稱為information-preserving，即轉換后的特征保留了原輸入的特征，而且轉換是可逆的。這正是pre-train希望做到的，通過encoding將輸入轉換為一些特征，而這些特征又可以復原原輸入x，實現information-preserving。所以，pre-training得到的權重初始值就應該滿足這樣的information-preserving特性。  如何在pre-training中得到這樣的權重初始值（即轉換特征）呢？方法是建立一個簡單的三層神經網絡（一個輸入層、一個隱藏層、一個輸出層），如下圖所示。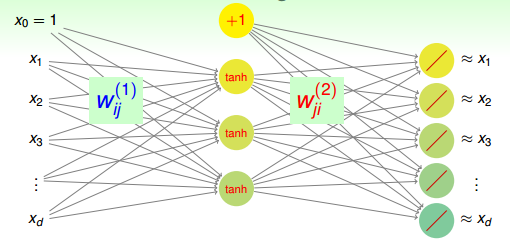  該神經網絡中，輸入層是原始數據（即待pre-training的數據），經過權重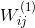得到隱藏層的輸出為原始數據新的表達方式（即轉換特征）。這些轉換特征再經過權重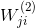得到輸出層，輸出層的結果要求跟原始數據類似，即輸入層和輸出層是近似相等的。整個網絡是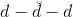 NNet結構。其核心在于“重構性”，從輸入層到隱藏層實現特征轉換，從隱藏層到輸出層實現重構，滿足上文所說的information-preserving的特性。這種結構的神經網絡我們稱之為autoencoder，輸入層到隱藏層對應編碼，而隱藏層到輸出層對應解碼。其中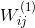，表示編碼權重，而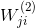表示解碼權重。整個過程類似于在學習如何近似逼近identity function。  那么為什么要使用這樣的結構來逼近identity function，有什么好處呢？首先對于監督式學習（supervised learning），這種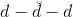的NNet結構中含有隱藏層。隱藏層的輸出實際上就是對原始數據合理的特征轉換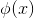，例如手寫識別中隱藏層分解的各個筆畫，包含了有用的信息。這樣就可以從數據中學習得到一些有用的具有代表性的信息。然后，對于非監督式學習（unsupervised learning），autoencoder也可以用來做density estimation。如果網絡最終的輸出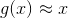，則表示密度較大；如果g(x)與x相差甚遠，則表示密度較小。也就是說可以根據g(x)與x的接近程度來估計測試數據是落在密度較大的地方還是密度較小的地方。這種方法同樣適用于outlier detection，異常檢測。這樣就可以從數據中學習得到一些典型的具有代表性的信息，找出哪些是典型資料，哪些不是典型資料。所以說，通過autoencoder不斷逼近identity function，對監督式學習和非監督式學習都具有深刻的物理意義和非常廣泛的應用。  其實，對于autoencoder來說，我們更關心的是網絡中間隱藏層，即原始數據的特征轉換以及特征轉換的編碼權重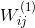。 Basic Autoencoder一般采用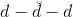的NNet結構，對應的error function是squared error，即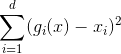。  basic autoencoder在結構上比較簡單，只有三層網絡，容易訓練和優化。各層之間的神經元數量上，通常限定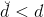，便于數據編碼。數據集可表示為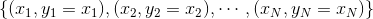：，即輸入輸出都是x，可以看成是非監督式學習。一個重要的限制條件是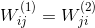，即編碼權重與解碼權重相同。這起到了regularization的作用，但是會讓計算復雜一些。  以上就是basic autoencoder的結構和一些限定條件。深度學習中，basic autoencoder的過程也就對應著pre-training的過程，使用這種方法，對無label的原始數據進行編碼和解碼，得到的編碼權重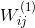就可以作為pre-trained的比較不錯的初始化權重，也就是作為深度學習中層與層之間的初始化權重。  我們在本節課第一部分就說了深度學習中非常重要的一步就是pre-training，即權重初始化，而autoencoder可以作為pre-training的一個合理方法。Pre-training的整個過程是：首先，autoencoder會對深度學習網絡第一層（即原始輸入）進行編碼和解碼，得到編碼權重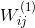，作為網絡第一層到第二層的的初始化權重；然后再對網絡第二層進行編碼和解碼，得到編碼權重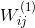，作為網絡第二層到第三層的初始化權重，以此類推，直到深度學習網絡中所有層與層之間都得到初始化權重。值得注意的是，對于l-1層的網絡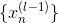，autoencoder中的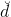應與下一層（即l層）的神經元個數相同。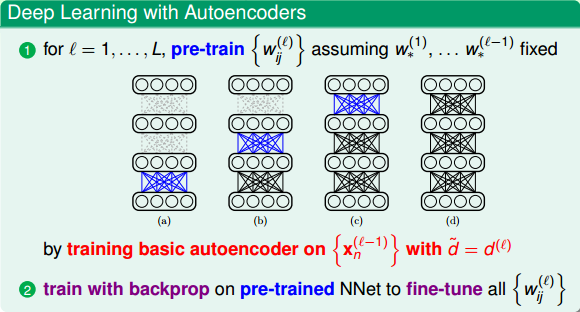  當然，除了basic autoencoder之外還有許多其它表現不錯的pre-training方法。這些方法大都采用不同的結構和正則化技巧來得到不同的’fancier’ autoencoders，這里不再贅述。 ### **Denoising Autoencoder** 上一部分，我們使用autoencoder解決了deep learning中pre-training的問題。接下來，我們將討論deep learning中有什么樣的regularization方式來控制模型的復雜度。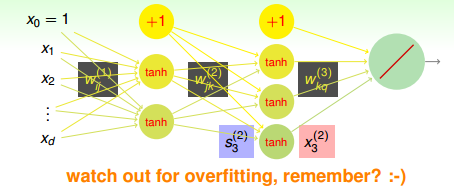  由于深度學習網絡中神經元和權重的個數非常多，相應的模型復雜度就會很大，因此，regularization非常必要。之前我門也介紹過一些regularization的方法，包括： * **structural decisions/constraints** * **weight decay or weight elimination regularizers** * **early stopping**  下面我們將介紹另外一種regularization的方式，它在deep learning和autoencoder中都有很好的效果。 首先我們來復習一下之前介紹的overfitting產生的原因有哪些。如下圖所示，我們知道overfitting與樣本數量、噪聲大小都有關系，數據量減少或者noise增大都會造成overfitting。如果數據量是固定的，那么noise的影響就非常大，此時，實現regularization的一個方法就是消除noise的影響。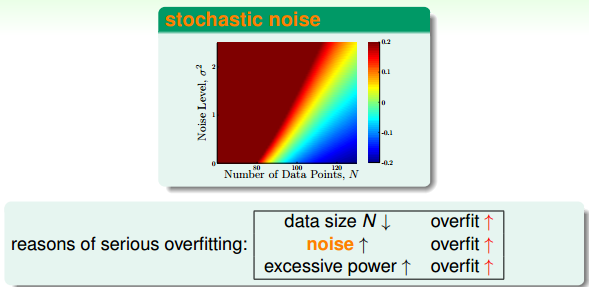  去除noise的一個簡單方法就是對數據進行cleaning/pruning的操作。但是，這種方法通常比較麻煩，費時費力。此處，有一種比較“瘋狂”的方法，就是往數據中添加一些noise。注意是添加noise！下面我們來解釋這樣做到底有什么作用。  這種做法的idea來自于如何建立一個健壯（robust）的autoencoder。在autoencoder中，編碼解碼后的輸出g(x)會非常接近真實樣本值x。此時，如果對原始輸入加入一些noise，對于健壯的autoencoder，編碼解碼后的輸出g(x)同樣會與真實樣本值x很接近。舉個例子，手寫識別中，通常情況下，寫的很規范的數字1經過autoencoder后能夠復原為數字1。如果原始圖片數字1歪斜或加入噪聲，經過autoencoder后應該仍然能夠解碼為數字1。這表明該autoencoder是robust的，一定程度上起到了抗噪聲和regularization的作用，這正是我們希望看到的。 所以，這就引出了denoising autoencoder的概念。denoising autoencoder不僅能實現編碼和解碼的功能，還能起到去噪聲、抗干擾的效果，即輸入一些混入noise的數據，經過autoencoder之后能夠得到較純凈的數據。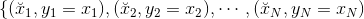這樣，autoencoder的樣本集為：  其中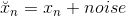，為混入噪聲的樣本，而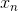為純凈樣本。 autoencoder訓練的目的就是讓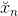經過編碼解碼后能夠復原為純凈的樣本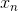。那么，在deep learning的pre-training中，如果使用這種denoising autoencoder，不僅能從純凈的樣本中編解碼得到純凈的樣本，還能從混入noise的樣本中編解碼得到純凈的樣本。這樣得到的權重初始值更好，因為它具有更好的抗噪聲能力，即健壯性好。實際應用中，denoising autoencoder非常有用，在訓練過程中，輸入混入人工noise，輸出純凈信號，讓模型本身具有抗噪聲的效果，讓模型健壯性更強，最關鍵的是起到了regularization的作用。  ### **Principal Component Analysis** 剛剛我們介紹的autoencoder是非線性的，因為其神經網絡模型中包含了tanh()函數。這部分我們將介紹linear autoencoder。nonlinear autoencoder通常比較復雜，多應用于深度學習中；而linear autoencoder通常比較簡單，我們熟知的主成分分析（Principal Component Analysis，PCA），其實跟linear autoencoder有很大的關系。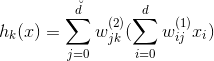 對于一個linear autoencoder，它的第k層輸出不包含tanh()函數，可表示為：  其中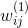，和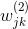分別是編碼權重和解碼權重。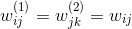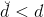而且，有三個限制條件，分別是： * **移除常數項，讓輸入輸出維度一致** * **編碼權重與解碼權重一致：** * ****  這樣，編碼權重用W表示，維度是d x 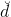，解碼權重用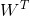表示。x的維度為d x 1。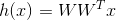則linear autoencoder hypothesis可經過下式計算得到：  其實，linear autoencoder hypothesis就應該近似于原始輸入x的值，即h(x)=x。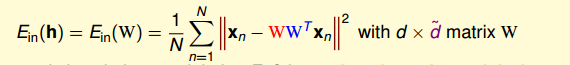根據這個，我們可以寫出它的error function：  我們的目的是計算出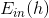最小化時對應的W。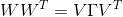根據線性代數知識，首先進行特征值分解：  其中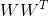是半正定矩陣。V矩陣滿足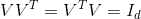。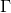是對角矩陣，對角線上有不超過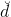個非零值（即為1），即對角線零值個數大于等于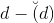。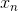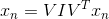根據特征值分解的思想，我們可以把進行類似分解：  其中，I是單位矩陣，維度為dxd。這樣，通過特征值分解我們就把對W的優化問題轉換成對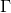和V的優化問題。  首先，我們來優化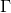值，表達式如下：  要求上式的最小化，可以轉化為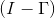越小越好，其結果對角線上零值越多越好，即I與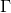越接近越好。因為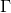的秩是小于等于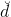的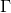，最多有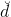個1。所以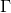，的最優解是其對角線上有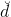個1。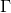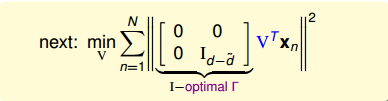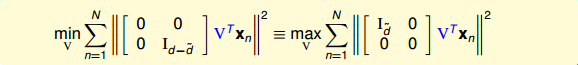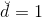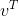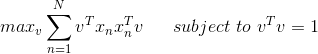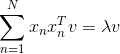  那么，的最優解已經得出，表達式變成：  這里的最小化問題似乎有點復雜，我們可以做一些轉換，把它變成最大化問題求解，轉換后的表達式為：  當時，中只有第一行有用，最大化問題轉化為：  引入拉格朗日因子，表達式的微分與條件微分應該是平行的，且由聯系起來，即：  根據線性代數的知識，很明顯能夠看出，v就是矩陣的特征向量，而就是相對應的特征值。我們要求的是最大值，所以最優解v就是矩陣最大特征值對應的特征向量。 當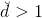時，求解方法是類似的，最優解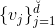就是矩陣前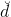大的特征值對應的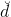個特征向量。 經過以上分析，我們得到了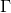和V的最優解。這就是linear autoencoder的編解碼推導過程。  值得一提的是，linear autoencoder與PCA推導過程十分相似。但有一點不同的是，一般情況下，PCA會對原始數據x進行處理，即減去其平均值。這是為了在推導過程中的便利。這兩種算法的計算流程大致如下：  linear autoencoder與PCA也有差別，PCA是基于統計學分析得到的。一般我們認為，將高維數據投影（降維）到低維空間中，應該保證數據本身的方差越大越好，而噪聲方差越小越好，而PCA正是基于此原理推導的。linear autoencoder與PCA都可以用來進行數據壓縮，但是PCA應用更加廣泛一些。  以上關于PCA的推導基本上是從幾何的角度，而沒有從代數角度進行詳細的數學推導。網上關于PCA的資料很多，這里附上一篇個人覺得講解得通俗易懂的PCA原理介紹：[PCA的數學原理](http://blog.codinglabs.org/articles/pca-tutorial.html)。有興趣的朋友可以看一看。 ### **總結** 本節課主要介紹了深度學習（deep learning）的數學模型，也是上節課講的神經網絡的延伸。由于深度學習網絡的復雜性，其建模優化是比較困難的。通常，我們可以從pre-training和regularization的角度來解決這些困難。首先，autoencoder可以得到比較不錯的初始化權重，起到pre-training的效果。然后，denoising autoencoder通過引入人工噪聲，訓練得到初始化權重，從而使模型本身抗噪聲能力更強，更具有健壯性，起到了regularization的效果。最后，我們介紹了linear autoencoder并從幾何角度詳述了其推導過程。linear autoencoder與PCA十分類似，都可以用來進行數據壓縮和數據降維處理。 **_注明：_** 文章中所有的圖片均來自臺灣大學林軒田《機器學習技法》課程