# 11 -- Gradient Boosted Decision Tree 上節課我們主要介紹了Random Forest算法模型。Random Forest就是通過bagging的方式將許多不同的decision tree組合起來。除此之外，在decision tree中加入了各種隨機性和多樣性，比如不同特征的線性組合等。RF還可以使用OOB樣本進行self-validation，而且可以通過permutation test進行feature selection。本節課將使用Adaptive Boosting的方法來研究decision tree的一些算法和模型。 ### **Adaptive Boosted Decision Tree** Random Forest的算法流程我們上節課也詳細介紹過，就是先通過bootstrapping“復制”原樣本集D，得到新的樣本集D’；然后對每個D’進行訓練得到不同的decision tree和對應的；最后再將所有的通過uniform的形式組合起來，即以投票的方式得到G。這里采用的Bagging的方式，也就是把每個的預測值直接相加。現在，如果將Bagging替換成AdaBoost，處理方式有些不同。首先每輪bootstrap得到的D’中每個樣本會賦予不同的權重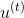；然后在每個decision tree中，利用這些權重訓練得到最好的；最后得出每個所占的權重，線性組合得到G。這種模型稱為AdaBoost-D Tree。  但是在AdaBoost-DTree中需要注意的一點是每個樣本的權重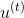。我們知道，在Adaptive Boosting中進行了bootstrap操作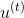，表示D中每個樣本在D’中出現的次數。但是在決策樹模型中，例如C&RT算法中并沒有引入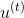。那么，如何在決策樹中引入這些權重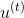來得到不同的而又不改變原來的決策樹算法呢？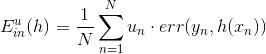 在Adaptive Boosting中，我們使用了weighted algorithm，形如：  每個犯錯誤的樣本點乘以相應的權重，求和再平均，最終得到了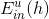。如果在決策樹中使用這種方法，將當前分支下犯錯誤的點賦予權重，每層分支都這樣做，會比較復雜，不易求解。為了簡化運算，保持決策樹算法本身的穩定性和封閉性，我們可以把決策樹算法當成一個黑盒子，即不改變其結構，不對算法本身進行修改，而從數據來源D’上做一些處理。按照這種思想，我們來看權重u實際上表示該樣本在bootstrap中出現的次數，反映了它出現的概率。那么可以根據u值，對原樣本集D進行一次重新的隨機sampling，也就是帶權重的隨機抽樣。sampling之后，會得到一個新的D’，D’中每個樣本出現的幾率與它權重u所占的比例應該是差不多接近的。因此，使用帶權重的sampling操作，得到了新的樣本數據集D’，可以直接代入決策樹進行訓練，從而無需改變決策樹算法結構。sampling可看成是bootstrap的反操作，這種對數據本身進行修改而不更改算法結構的方法非常重要！  所以，AdaBoost-DTree結合了AdaBoost和DTree，但是做了一點小小的改變，就是使用sampling替代權重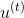，效果是相同的。  上面我們通過使用sampling，將不同的樣本集代入決策樹中，得到不同的。除此之外，我們還要確定每個所占的權重。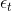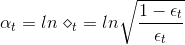之前我們在AdaBoost中已經介紹過，首先算出每個的錯誤率，然后計算權重：  如果現在有一棵完全長成的樹（fully grown tree），由所有的樣本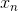訓練得到。若每個樣本都不相同的話，一刀刀切割分支，直到所有的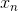都被完全分開。這時候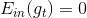，，加權的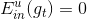而且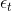也為0，從而得到權重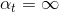。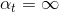表示該所占的權重無限大，相當于它一個就決定了G結構，是一種autocracy，而其它的對G沒有影響。  顯然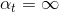不是我們想看到的，因為autocracy總是不好的，我們希望使用aggregation將不同的結合起來，發揮集體智慧來得到最好的模型G。首先，我們來看一下什么原因造成了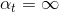。有兩個原因：一個是使用了所有的樣本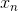進行訓練；一個是樹的分支過多，fully grown。針對這兩個原因，我們可以對樹做一些修剪（pruned），比如只使用一部分樣本，這在sampling的操作中已經起到這類作用，因為必然有些樣本沒有被采樣到。除此之外，我們還可以限制樹的高度，讓分支不要那么多，從而避免樹fully grown。  因此，AdaBoost-DTree使用的是pruned DTree，也就是說將這些預測效果較弱的樹結合起來，得到最好的G，避免出現autocracy。  剛才我們說了可以限制樹的高度，那索性將樹的高度限制到最低，即只有1層高的時候，有什么特性呢？當樹高為1的時候，整棵樹只有兩個分支，切割一次即可。如果impurity是binary classification error的話，那么此時的AdaBoost-DTree就跟AdaBoost-Stump沒什么兩樣。也就是說AdaBoost-Stump是AdaBoost-DTree的一種特殊情況。  值得一提是，如果樹高為1時，通常較難遇到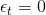的情況，且一般不采用sampling的操作，而是直接將權重u代入到算法中。這是因為此時的AdaBoost-DTree就相當于是AdaBoost-Stump，而AdaBoost-Stump就是直接使用u來優化模型的。 ### **Optimization View of AdaBoost** 接下來，我們繼續將繼續探討AdaBoost算法的一些奧妙之處。我們知道AdaBoost中的權重的迭代計算如下所示：  之前對于incorrect樣本和correct樣本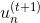，的表達式不同。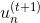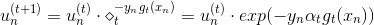現在，把兩種情況結合起來，將寫成一種簡化的形式：  其中，對于incorrect樣本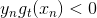，，對于correct樣本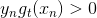，。從上式可以看出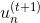，由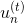與某個常數相乘得到。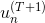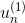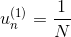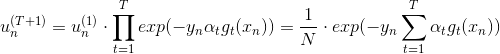所以，最后一輪更新的可以寫成的級聯形式，我們之前令，則有如下推導：  上式中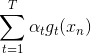被稱為voting score，最終的模型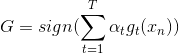。可以看出，在AdaBoost中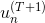，與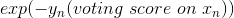成正比。  接下來我們繼續看一下voting score中蘊含了哪些內容。如下圖所示，voting score由許多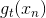乘以各自的系數線性組合而成。從另外一個角度來看，我們可以把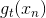看成是對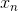的特征轉換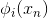，就是線性模型中的權重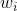。看到這里，我們回憶起之前SVM中，w與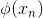的乘積再除以w的長度就是margin，即點到邊界的距離。另外，乘積項再與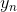相乘，表示點的位置是在正確的那一側還是錯誤的那一側。所以，回過頭來，這里的voting score實際上可以看成是沒有正規化（沒有除以w的長度）的距離，即可以看成是該點到分類邊界距離的一種衡量。從效果上說，距離越大越好，也就是說voting score要盡可能大一些。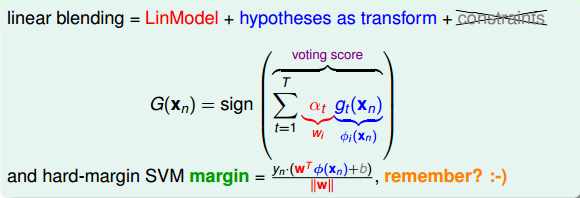  我們再來看，若voting score與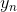相乘，則表示一個有對錯之分的距離。也就是說，如果二者相乘是負數，則表示該點在錯誤的一邊，分類錯誤；如果二者相乘是正數，則表示該點在正確的一邊，分類正確。所以，我們算法的目的就是讓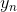與voting score的乘積是正的，而且越大越好。那么在剛剛推導的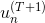中，得到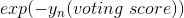越小越好，從而得到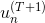越小越好。也就是說，如果voting score表現不錯，與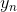的乘積越大的話，那么相應的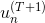應該是最小的。  那么在AdaBoost中，隨著每輪學習的進行，每個樣本的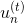是逐漸減小的，直到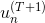最小。以上是從單個樣本點來看的。總體來看，所有樣本的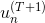之和應該也是最小的。我們的目標就是在最后一輪（T+1）學習后，讓所有樣本的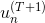之和盡可能地小。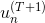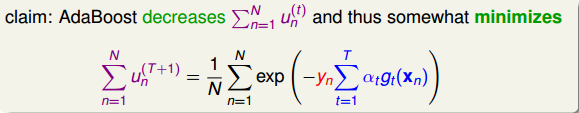之和表示為如下形式：  上式中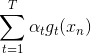，被稱為linear score，用s表示。對于0/1 error：若ys<0，則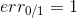；若ys>=0，則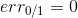。如下圖右邊黑色折線所示。對于上式中提到的指數error，即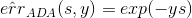，隨著ys的增加，error單調下降，且始終落在0/1 error折線的上面。如下圖右邊藍色曲線所示。很明顯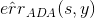，可以看成是0/1 error的上界。所以，我們可以使用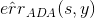來替代0/1 error，能達到同樣的效果。從這點來說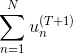，可以看成是一種error measure，而我們的目標就是讓其最小化，求出最小值時對應的各個和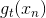。  下面我們來研究如何讓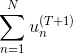取得最小值，思考是否能用梯度下降（gradient descent）的方法來進行求解。我們之前介紹過gradient descent的核心是在某點處做一階泰勒展開：  其中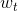，是泰勒展開的位置，v是所要求的下降的最好方向，它是梯度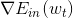的反方向，而是每次前進的步長。則每次沿著當前梯度的反方向走一小步，就會不斷逼近谷底（最小值）。這就是梯度下降算法所做的事情。 現在，我們對做梯度下降算法處理，區別是這里的方向是一個函數，而不是一個向量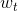。其實，函數和向量的唯一區別就是一個下標是連續的，另一個下標是離散的，二者在梯度下降算法應用上并沒有大的區別。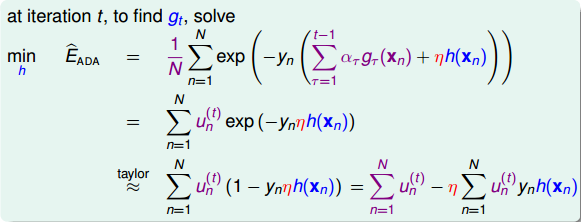因此，按照梯度下降算法的展開式，做出如下推導：  上式中，表示當前的方向，它是一個矩，是沿著當前方向前進的步長。我們要求出這樣的和，使得是在不斷減小的。當取得最小值的時候，那么所有的方向即最佳的和就都解出來了。上述推導使用了在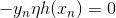處的一階泰勒展開近似。這樣經過推導之后，被分解為兩個部分，一個是前N個u之和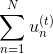，也就是當前所有的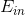之和；另外一個是包含下一步前進的方向和步進長度的項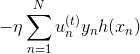。的這種形式與gradient descent的形式基本是一致的。 那么接下來，如果要最小化的話，就要讓第二項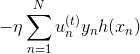越小越好。則我們的目標就是找到一個好的（即好的方向）來最小化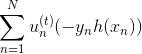，此時先忽略步進長度。  對于binary classification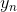，和均限定取值-1或+1兩種。我們對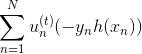做一些推導和平移運算：  最終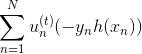化簡為兩項組成，一項是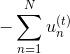；另一項是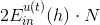。則最小化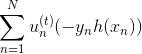就轉化為最小化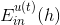。要讓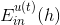最小化，正是由AdaBoost中的base algorithm所做的事情。所以說，AdaBoost中的base algorithm正好幫我們找到了梯度下降中下一步最好的函數方向。  以上就是從數學上，從gradient descent角度驗證了AdaBoost中使用base algorithm得到的就是讓減小的方向，只不過這個方向是一個函數而不是向量。 在解決了方向問題后，我們需要考慮步進長度如何選取。方法是在確定方向后，選取合適的，使取得最小值。也就是說，把看成是步進長度的函數，目標是找到最小化時對應的值。  目的是找到在最佳方向上的最大步進長度，也就是steepest decent。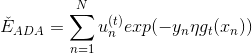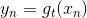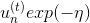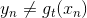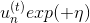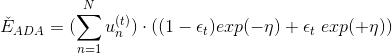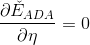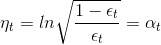我們先把表達式寫下來：  上式中，有兩種情況需要考慮： * **： correct** * **： incorrect** 經過推導，可得：   然后對求導，令，得：  由此看出，最大的步進長度就是，即AdaBoost中計算所占的權重。所以，AdaBoost算法所做的其實是在gradient descent上找到下降最快的方向和最大的步進長度。這里的方向就是，它是一個函數，而步進長度就是。也就是說，在AdaBoost中確定和的過程就相當于在gradient descent上尋找最快的下降方向和最大的步進長度。 ### **Gradient Boosting** 前面我們從gradient descent的角度來重新介紹了AdaBoost的最優化求解方法。整個過程可以概括為：  以上是針對binary classification問題。如果往更一般的情況進行推廣，對于不同的error function，比如logistic error function或者regression中的squared error function，那么這種做法是否仍然有效呢？這種情況下的GradientBoost可以寫成如下形式：  仍然按照gradient descent的思想，上式中，是下一步前進的方向，是步進長度。此時的error function不是前面所講的exp了，而是任意的一種error function。因此，對應的hypothesis也不再是binary classification，最常用的是實數輸出的hypothesis，例如regression。最終的目標也是求解最佳的前進方向和最快的步進長度。  接下來，我們就來看看如何求解regression的GradientBoost問題。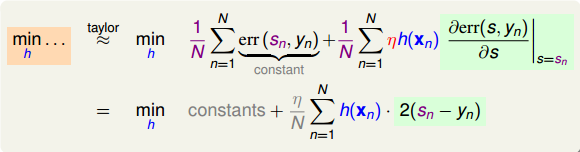它的表達式如下所示：  利用梯度下降的思想，我們把上式進行一階泰勒展開，寫成梯度的形式：  上式中，由于regression的error function是squared的，所以，對s的導數就是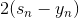。其中標注灰色的部分表示常數，對最小化求解并沒有影響，所以可以忽略。很明顯，要使上式最小化，只要令是梯度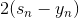的反方向就行了，即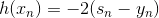。但是直接這樣賦值，并沒有對的大小進行限制，一般不直接利用這個關系求出。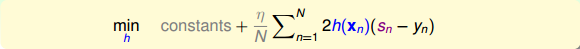  實際上的大小并不重要，因為有步進長度。那么，我們上面的最小化問題中需要對的大小做些限制。限制的一種簡單做法是把的大小當成一個懲罰項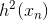（）添加到上面的最小化問題中，這種做法與regularization類似。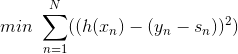如下圖所示，經過推導和整理，忽略常數項，我們得到最關心的式子是：  上式是一個完全平方項之和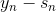，表示當前第n個樣本真實值和預測值的差，稱之為余數。余數表示當前預測能夠做到的效果與真實值的差值是多少。那么，如果我們想要讓上式最小化，求出對應的的話，只要讓盡可能地接近余數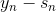即可。在平方誤差上盡可能接近其實很簡單，就是使用regression的方法，對所有N個點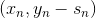做squared-error的regression，得到的回歸方程就是我們要求的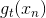。  以上就是使用GradientBoost的思想來解決regression問題的方法，其中應用了一個非常重要的概念，就是余數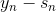。根據這些余數做regression，得到好的矩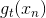，方向函數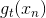也就是由余數決定的。  在求出最好的方向函數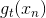之后，就要來求相應的步進長度。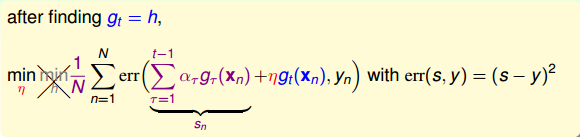表達式如下：  同樣，對上式進行推導和化簡，得到如下表達式：  上式中也包含了余數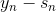，其中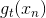可以看成是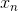的特征轉換，是已知量。那么，如果我們想要讓上式最小化，求出對應的的話，只要讓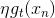盡可能地接近余數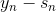即可。顯然，這也是一個regression問題，而且是一個很簡單的形如y=ax的線性回歸，只有一個未知數。只要對所有N個點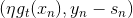做squared-error的linear regression，利用梯度下降算法就能得到最佳的。 將上述這些概念合并到一起，我們就得到了一個最終的演算法Gradient Boosted Decision Tree(GBDT)。可能有人會問，我們剛才一直沒有說到Decison Tree，只是講到了GradientBoost啊？下面我們來看看Decison Tree究竟是在哪出現并使用的。其實剛剛我們在計算方向函數的時候，是對所有N個點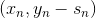做squared-error的regression。那么這個回歸算法就可以是決策樹C&RT模型（決策樹也可以用來做regression）。這樣，就引入了Decision Tree，并將GradientBoost和Decision Tree結合起來，構成了真正的GBDT算法。GBDT算法的基本流程圖如下所示：  值得注意的是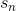，的初始值一般均設為0，即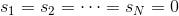。每輪迭代中，方向函數通過C&RT算法做regression，進行求解；步進長度通過簡單的單參數線性回歸進行求解；然后每輪更新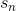的值，即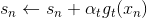。T輪迭代結束后，最終得到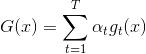。 值得一提的是，本節課第一部分介紹的AdaBoost-DTree是解決binary classification問題，而此處介紹的GBDT是解決regression問題。二者具有一定的相似性，可以說GBDT就是AdaBoost-DTree的regression版本。  ### **Summary of Aggregation Models** 從機器學習技法課程的第7節課筆記到現在的第11節課筆記，我們已經介紹完所有的aggregation模型了。接下來，我們將對這些內容進行一個簡單的總結和概括。 首先，我們介紹了blending。blending就是將所有已知的 aggregate結合起來，發揮集體的智慧得到G。值得注意的一點是這里的都是已知的。blending通常有三種形式： * **uniform：簡單地計算所有的平均值** * **non-uniform：所有的線性組合** * **conditional：所有的非線性組合** 其中，uniform采用投票、求平均的形式更注重穩定性；而non-uniform和conditional追求的更復雜準確的模型，但存在過擬合的危險。  剛才講的blending是建立在所有已知的情況。那如果所有未知的情況，對應的就是learning模型，做法就是一邊學，一邊將它們結合起來。learning通常也有三種形式（與blending的三種形式一一對應）： * **Bagging：通過bootstrap方法，得到不同，計算所有的平均值** * **AdaBoost：通過bootstrap方法，得到不同，所有的線性組合** * **Decision Tree：通過數據分割的形式得到不同的，所有的非線性組合** 然后，本節課我們將AdaBoost延伸到另一個模型GradientBoost。對于regression問題，GradientBoost通過residual fitting的方式得到最佳的方向函數和步進長度。  除了這些基本的aggregation模型之外，我們還可以把某些模型結合起來得到新的aggregation模型。例如，Bagging與Decision Tree結合起來組成了Random Forest。Random Forest中的Decision Tree是比較“茂盛”的樹，即每個樹的都比較強一些。AdaBoost與Decision Tree結合組成了AdaBoost-DTree。AdaBoost-DTree的Decision Tree是比較“矮弱”的樹，即每個樹的都比較弱一些，由AdaBoost將所有弱弱的樹結合起來，讓綜合能力更強。同樣，GradientBoost與Decision Tree結合就構成了經典的算法GBDT。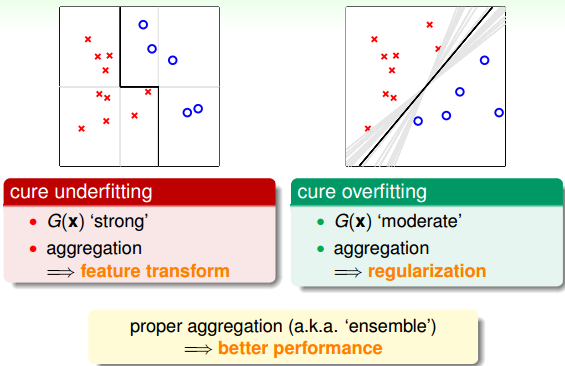  Aggregation的核心是將所有的結合起來，融合到一起，即集體智慧的思想。這種做法之所以能得到很好的模型G，是因為aggregation具有兩個方面的優點：cure underfitting和cure overfitting。 第一，aggregation models有助于防止欠擬合（underfitting）。它把所有比較弱的結合起來，利用集體智慧來獲得比較好的模型G。aggregation就相當于是feature transform，來獲得復雜的學習模型。 第二，aggregation models有助于防止過擬合（overfitting）。它把所有進行組合，容易得到一個比較中庸的模型，類似于SVM的large margin一樣的效果，從而避免一些極端情況包括過擬合的發生。從這個角度來說，aggregation起到了regularization的效果。 由于aggregation具有這兩個方面的優點，所以在實際應用中aggregation models都有很好的表現。  ### **總結** 本節課主要介紹了Gradient Boosted Decision Tree。首先講如何將AdaBoost與Decision Tree結合起來，即通過sampling和pruning的方法得到AdaBoost-D Tree模型。然后，我們從optimization的角度來看AdaBoost，找到好的hypothesis也就是找到一個好的方向，找到權重也就是找到合適的步進長度。接著，我們從binary classification的0/1 error推廣到其它的error function，從Gradient Boosting角度推導了regression的squared error形式。Gradient Boosting其實就是不斷迭代，做residual fitting。并將其與Decision Tree算法結合，得到了經典的GBDT算法。最后，我們將所有的aggregation models做了總結和概括，這些模型有的能防止欠擬合有的能防止過擬合，應用十分廣泛。 **_注明：_** 文章中所有的圖片均來自臺灣大學林軒田《機器學習技法》課程