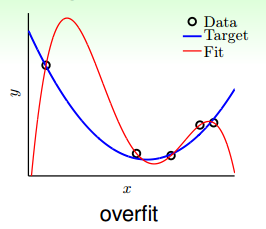
# 14 -- Regularization 上節課我們介紹了過擬合發生的原因：excessive power, stochastic/deterministic noise 和limited data。并介紹了解決overfitting的簡單方法。本節課，我們將介紹解決overfitting的另一種非常重要的方法：Regularization規則化。 ### **一、Regularized Hypothesis Set** 先來看一個典型的overfitting的例子：  如圖所示，在數據量不夠大的情況下，如果我們使用一個高階多項式（圖中紅色曲線所示），例如10階，對目標函數（藍色曲線）進行擬合。擬合曲線波動很大，雖然很小，但是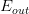很大，也就造成了過擬合現象。 那么如何對過擬合現象進行修正，使hypothesis更接近于target function呢？一種方法就是regularized fit。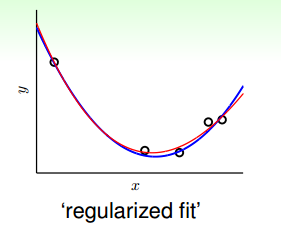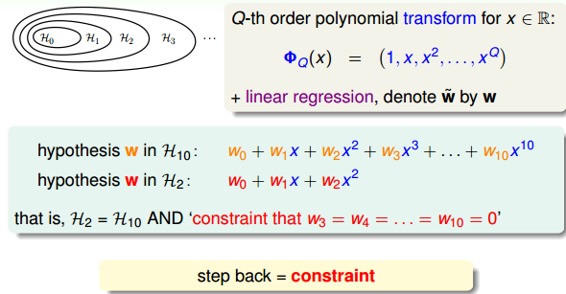  這種方法得到的紅色fit曲線，要比overfit的紅色曲線平滑很多，更接近與目標函數，它的階數要更低一些。那么問題就變成了我們要把高階（10階）的hypothesis sets轉換為低階（2階）的hypothesis sets。通過下圖我們發現，不同階數的hypothesis存在如下包含關系：  我們發現10階多項式hypothesis sets里包含了2階多項式hypothesis sets的所有項，那么在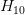中加入一些限定條件，使它近似為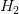即可。這種函數近似曾被稱之為不適定問題（ill-posed problem）。 如何從10階轉換為2階呢？首先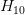，可表示為： 而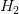可表示為： 所以，如果限定條件是，那么就有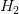。也就是說，對于高階的hypothesis，為了防止過擬合，我們可以將其高階部分的權重w限制為0，這樣，就相當于從高階的形式轉換為低階，fit波形更加平滑，不容易發生過擬合。  那有一個問題，令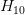高階權重w為0，為什么不直接使用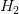呢？這樣做的目的是拓展我們的視野，為即將討論的問題做準備。剛剛我們討論的限制是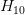高階部分的權重w限制為0，這是比較苛刻的一種限制。下面，我們把這個限制條件變得更寬松一點，即令任意8個權重w為0，并不非要限定，這個Looser Constraint可以寫成： 也就只是限定了w不為0的個數，并不限定必須是高階的w。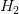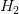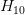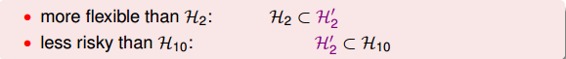這種hypothesis記為，稱為sparse hypothesis set，它與和的關系為：  Looser Constraint對應的hypothesis應該更好解一些，但事實是sparse hypothesis set 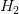被證明也是NP-hard，求解非常困難。所以，還要轉換為另一種易于求解的限定條件。 那么，我們尋找一種更容易求解的寬松的限定條件Softer Constraint，即： 其中，C是常數，也就是說，所有的權重w的平方和的大小不超過C，我們把這種hypothesis sets記為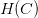。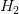 與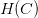的關系是，它們之間有重疊，有交集的部分，但是沒有完全包含的關系，也不一定相等。對應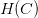，C值越大，限定的范圍越大，即越寬松： 當C無限大的時候，即限定條件非常寬松，相當于沒有加上任何限制，就與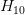沒有什么兩樣。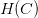稱為regularized hypothesis set，這種形式的限定條件是可以進行求解的，我們把求解的滿足限定條件的權重w記為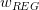。接下來就要探討如何求解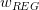。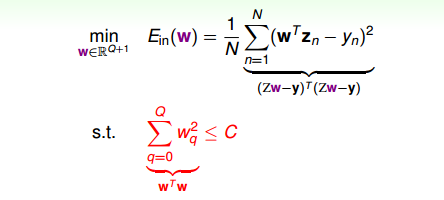 ### **二、Weight Decay Regularization** 現在，針對H(c)，即加上限定條件，我們的問題變成：  我們的目的是計算的最小值，限定條件是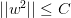。這個限定條件從幾何角度上的意思是，權重w被限定在半徑為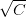的圓內，而球外的w都不符合要求，即便它是靠近梯度為零的w。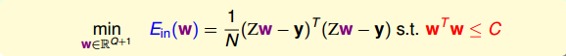  下面用一張圖來解釋在限定條件下，最小化的過程：  如上圖所示，假設在空間中的一點w，根據梯度下降算法，w會朝著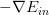的方向移動（圖中藍色箭頭指示的方向），在沒有限定條件的情況下，w最終會取得最小值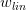，即“谷底”的位置。現在，加上限定條件，即w被限定在半徑為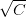的圓內，w距離原點的距離不能超過圓的半徑，球如圖中紅色圓圈所示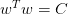。那么，這種情況下，w不能到達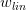的位置，最大只能位于圓上，沿著圓的切線方向移動（圖中綠色箭頭指示的方向）。與綠色向量垂直的向量（圖中紅色箭頭指示的方向）是圓切線的法向量，即w的方向，w不能靠近紅色箭頭方向移動。那么隨著迭代優化過程，只要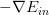與w點切線方向不垂直，那么根據向量知識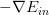，一定在w點切線方向上有不為零的分量，即w點會繼續移動。只有當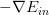與綠色切線垂直，即與紅色法向量平行的時候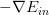，在切線方向上沒有不為零的分量了，也就表示這時w達到了最優解的位置。 有了這個平行的概念，我們就得到了獲得最優解需要滿足的性質： 上面公式中的稱為Lagrange multiplier，是用來解有條件的最佳化問題常用的數學工具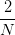，是方便后面公式推導。那么我們的目標就變成了求解滿足上面公式的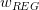。 之前我們推導過，線性回歸的的表達式為： 計算梯度，并代入到平行條件中，得到： 這是一個線性方程式，直接得到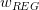為： 上式中包含了求逆矩陣的過程，因為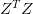是半正定矩陣，如果大于零，那么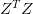一定是正定矩陣，即一定可逆。另外提一下，統計學上把這叫做ridge regression，可以看成是linear regression的進階版。 如果對于更一般的情況，例如邏輯回歸問題中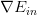，不是線性的，那么將其代入平行條件中得到的就不是一個線性方程式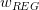，不易求解。下面我們從另一個角度來看一下平行等式： 已知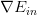是對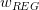的導數，而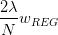也可以看成是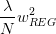的導數。那么平行等式左邊可以看成一個函數的導數，導數為零，即求該函數的最小值。也就是說，問題轉換為最小化該函數： 該函數中第二項就是限定條件regularizer，也稱為weight-decay regularization。我們把這個函數稱為Augmented Error，即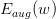。 如果不為零，對應于加上了限定條件，若等于零，則對應于沒有任何限定條件，問題轉換成之前的最小化。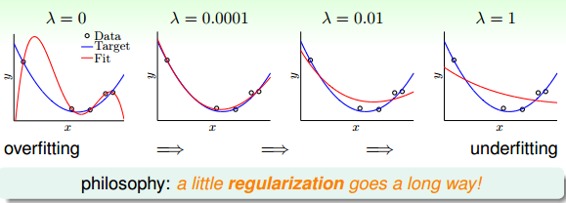 下面給出一個曲線擬合的例子，取不同的值時，得到的曲線也不相同：  從圖中可以看出，當時，發生了過擬合；當時，擬合的效果很好；當和時，發生了欠擬合。我們可以把看成是一種penality，即對hypothesis復雜度的懲罰，越大，w就越小，對應于C值越小，即這種懲罰越大，擬合曲線就會越平滑，高階項就會削弱，容易發生欠擬合。一般取比較小的值就能達到良好的擬合效果，過大過小都有問題，但究竟取什么值，要根據具體訓練數據和模型進行分析與調試。  事實上，這種regularization不僅可以用在多項式的hypothesis中，還可以應用在logistic regression等其他hypothesis中，都可以達到防止過擬合的效果。 我們目前討論的多項式是形如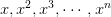的形式，若x的范圍限定在[-1,1]之間，那么可能導致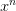相對于低階的值要小得多，則其對于的w非常大，相當于要給高階項設置很大的懲罰。為了避免出現這種數據大小差別很大的情況，可以使用Legendre Polynomials代替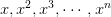這種形式，Legendre Polynomials各項之間是正交的，用它進行多項式擬合的效果更好。關于Legendre Polynomials的概念這里不詳細介紹，有興趣的童鞋可以看一下[維基百科](https://en.wikipedia.org/wiki/Legendre_polynomials)。 ### **三、Regularization and VC Theory** 下面我們研究一下Regularization與VC理論之間的關系。Augmented Error表達式如下： VC Bound表示為： 其中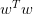表示的是單個hypothesis的復雜度，記為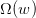；而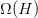表示整個hypothesis set的復雜度。根據Augmented Error和VC Bound的表達式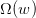，包含于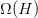之內，所以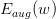，比更接近于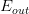，即更好地代表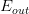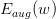，與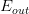之間的誤差更小。  根據VC Dimension理論，整個hypothesis set的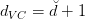，這是因為所有的w都考慮了，沒有任何限制條件。而引入限定條件的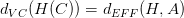，即有效的VC dimension。也就是說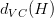，比較大，因為它代表了整個hypothesis set，但是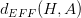比較小，因為由于regularized的影響，限定了w只取一小部分。其中A表示regularized算法。當時，有： 這些與實際情況是相符的，比如對多項式擬合模型，當時，所有的w都給予考慮，相應的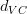很大，容易發生過擬合。當且越來越大時，很多w將被舍棄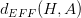，減小，擬合曲線越來越平滑，容易發生欠擬合。 ### **四、General Regularizers** 那么通用的Regularizers，即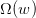，應該選擇什么樣的形式呢？一般地，我們會朝著目標函數的方向進行選取。有三種方式： * **target-dependent** * **plausible** * **friendly**  其實這三種方法跟之前error measure類似，其也有三種方法： * **user-dependent** * **plausible** * **friendly** regularizer與error measure是機器學習模型設計中的重要步驟。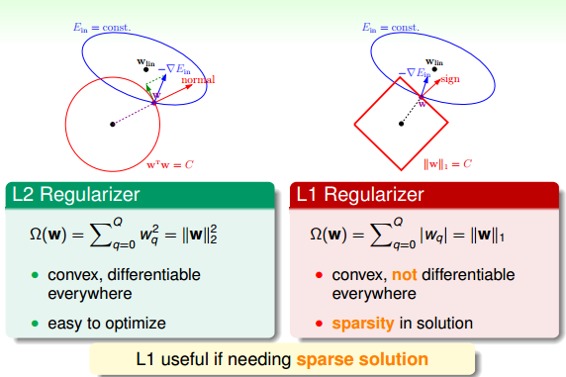  接下來，介紹兩種Regularizer：L2和L1。L2 Regularizer一般比較通用，其形式如下： 這種形式的regularizer計算的是w的平方和，是凸函數，比較平滑，易于微分，容易進行最優化計算。 L1 Regularizer的表達式如下： L1計算的不是w的平方和，而是絕對值和，即長度和，也是凸函數。已知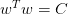圍成的是圓形，而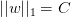圍成的是正方形，那么在正方形的四個頂點處，是不可微分的（不像圓形，處處可微分）。根據之前介紹的平行等式推導過程，對應這種正方形，它的解大都位于四個頂點處（不太理解，歡迎補充賜教），因為正方形邊界處的w絕對值都不為零，若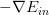不與其平行，那么w就會向頂點處移動，頂點處的許多w分量為零，所以，L1 Regularizer的解是稀疏的，稱為sparsity。優點是計算速度快。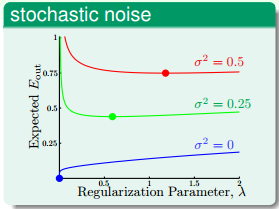  下面來看一下如何取值，首先，若stochastic noise不同，那么一般情況下，取值有如下特點：  從圖中可以看出，stochastic noise越大，越大。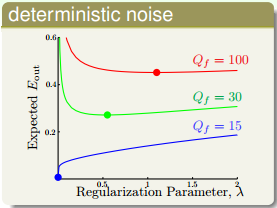 另一種情況，不同的deterministic noise，取值有如下特點：  從圖中可以看出，deterministic noise越大，越大。 以上兩種noise的情況下，都是noise越大，相應的也就越大。這也很好理解，如果在開車的情況下，路況也不好，即noise越多，那么就越會踩剎車，這里踩剎車指的就是regularization。但是大多數情況下，noise是不可知的，這種情況下如何選擇？這部分內容，我們下節課將會討論。 ### **五、總結** 本節課主要介紹了Regularization。首先，原來的hypothesis set加上一些限制條件，就成了Regularized Hypothesis Set。加上限制條件之后，我們就可以把問題轉化為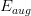最小化問題，即把w的平方加進去。這種過程，實際上回降低VC Dimension。最后，介紹regularization是通用的機器學習工具，設計方法通常包括target-dependent，plausible，friendly等等。下節課將介紹如何選取合適的來建立最佳擬合模型。 **_注明：_** 文章中所有的圖片均來自臺灣大學林軒田《機器學習基石》課程