# 12 -- Neural Network 上節課我們主要介紹了Gradient Boosted Decision Tree。GBDT通過使用functional gradient的方法得到一棵一棵不同的樹，然后再使用steepest descent的方式給予每棵樹不同的權重，最后可以用來處理任何而定error measure。上節課介紹的GBDT是以regression為例進行介紹的，使用的是squared error measure。本節課講介紹一種出現時間較早，但當下又非常火的一種機器算法模型，就是神經網絡（Neural Network）。 ### **Motivation** 在之前的機器學習基石課程中，我們就接觸過Perceptron模型了，例如PLA算法。Perceptron就是在矩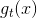外面加上一個sign函數，取值為{-1,+1}。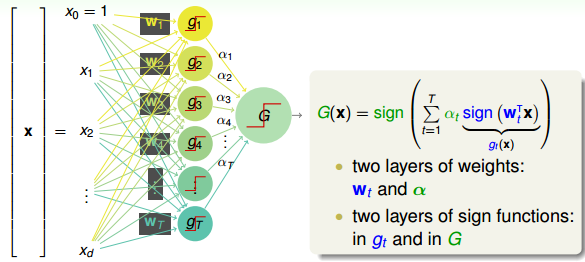現在，如果把許多perceptrons線性組合起來，得到的模型G就如下圖所示：  將左邊的輸入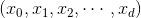與T個不同的權重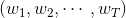相乘（每個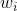是d+1維的），得到T個不同的perceptrons為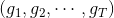。最后，每個給予不同的權重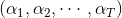，線性組合得到G。G也是一個perceptron模型。 從結構上來說，上面這個模型包含了兩層的權重，分別是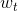和。同時也包含了兩層的sign函數，分別是和G。那么這樣一個由許多感知機linear aggregation的模型能實現什么樣的boundary呢？ 舉個簡單的例子，如下圖所示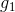，和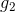分別是平面上兩個perceptrons。其中，紅色表示-1，藍色表示+1。這兩個perceptrons線性組合可能得到下圖右側的模型，這表示的是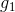和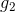進行與（AND）的操作，藍色區域表示+1。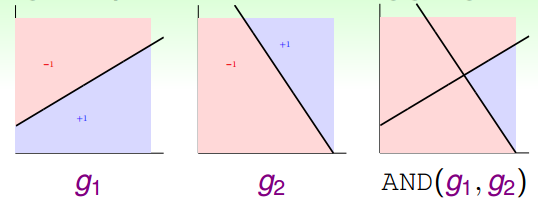  如何通過感知機模型來實現上述的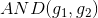邏輯操作呢？一種方法是令第二層中的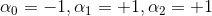。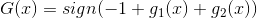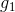這樣，G(x)就可表示為：  和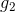的取值是{-1,+1}，當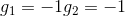時，G(x)=0；當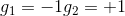時，G(x)=0；當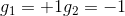時，G(x)=0；當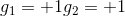時，G(x)=1。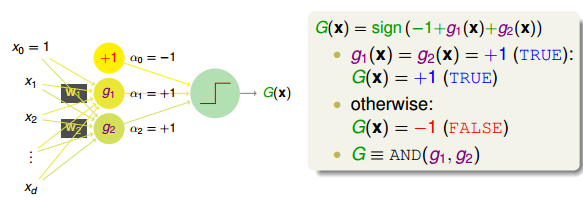感知機模型如下所示：  這個例子說明了一些簡單的線性邊界，如上面的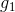和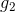，在經過一層感知機模型，經線性組合后，可以得到一些非線性的復雜邊界（AND運算）G(x)。 除此之外，或（OR）運算和非（NOT）運算都可以由感知機建立相應的模型，非常簡單。 所以說，linear aggregation of perceptrons實際上是非常powerful的模型同時也是非常complicated模型。再看下面一個例子，如果二維平面上有個圓形區域，圓內表示+1，圓外表示-1。這樣復雜的圓形邊界是沒有辦法使用單一perceptron來解決的。如果使用8個perceptrons，用剛才的方法線性組合起來，能夠得到一個很接近圓形的邊界（八邊形）。如果使用16個perceptrons，那么得到的邊界更接近圓形（十六邊形）。因此，使用的perceptrons越多，就能得到各種任意的convex set，即凸多邊形邊界。之前我們在機器學習基石中介紹過，convex set的VC Dimension趨向于無窮大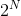（）。這表示只要perceptrons夠多，我們能得到任意可能的情況，可能的模型。但是，這樣的壞處是模型復雜度可能會變得很大，從而造成過擬合（overfitting）。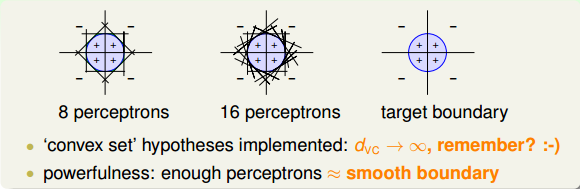  總的來說，足夠數目的perceptrons線性組合能夠得到比較平滑的邊界和穩定的模型，這也是aggregation的特點之一。 但是，也有單層perceptrons線性組合做不到的事情。例如剛才我們將的AND、OR、NOT三種邏輯運算都可以由單層perceptrons做到，而如果是異或（XOR）操作，就沒有辦法只用單層perceptrons實現。這是因為XOR得到的是非線性可分的區域，如下圖所示，沒有辦法由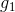和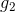線性組合實現。所以說linear aggregation of perceptrons模型的復雜度還是有限制的。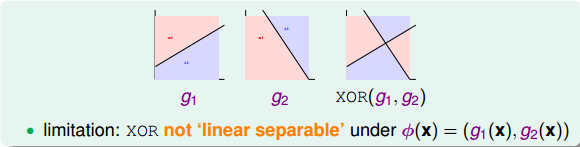  那么，為了實現XOR操作，可以使用多層perceptrons，也就是說一次transform不行，我們就用多層的transform，這其實就是Basic Neural Network的基本原型。下面我們就嘗試使用兩層perceptrons來實現XOR的操作。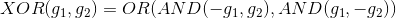 首先，根據布爾運算，異或XOR操作可以拆分成：  這種拆分實際上就包含了兩層transform。第一層僅有AND操作，第二層是OR操作。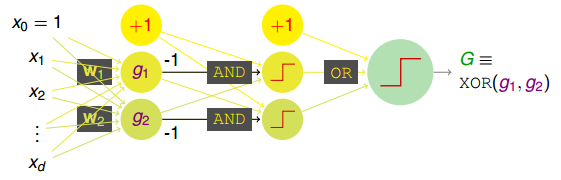這種兩層的感知機模型如下所示：  這樣，從AND操作到XOR操作，從簡單的aggregation of perceptrons到multi-layer perceptrons，感知機層數在增加，模型的復雜度也在增加，使最后得到的G能更容易解決一些非線性的復雜問題。這就是基本神經網絡的基本模型。  順便提一下，這里所說的感知機模型實際上就是在模仿人類的神經元模型（這就是Neural Network名稱的由來）。感知機模型每個節點的輸入就對應神經元的樹突dendrite，感知機每個節點的輸出就對應神經元的軸突axon。 ### **Neural Network Hypothesis** 上一部分我們介紹的這種感知機模型其實就是Neural Network。輸入部分經過一層一層的運算，相當于一層一層的transform，最后通過最后一層的權重，得到一個分數score。即在OUTPUT層，輸出的就是一個線性模型。得到s后，下一步再進行處理。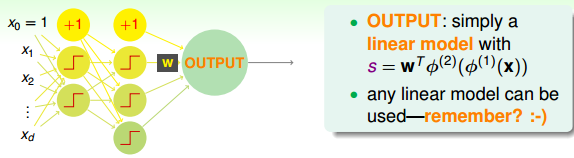  我們之前已經介紹過三種線性模型：linear classification，linear regression，logistic regression。那么，對于OUTPUT層的分數s，根據具體問題，可以選擇最合適的線性模型。如果是binary classification問題，可以選擇linear classification模型；如果是linear regression問題，可以選擇linear regression模型；如果是soft classification問題，則可以選擇logistic regression模型。本節課接下來將以linear regression為例，選擇squared error來進行衡量。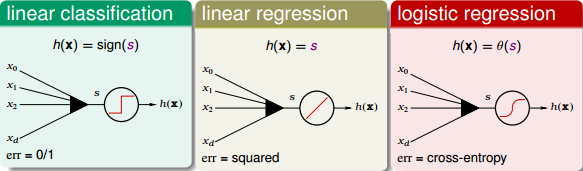  上面講的是OUTPUT層，對于中間層，每個節點對應一個perceptron，都有一個transform運算。上文我們已經介紹過的transformation function是階梯函數sign()。那除了sign()函數外，有沒有其他的transformation function呢？ 如果每個節點的transformation function都是線性運算（跟OUTPUT端一樣），那么由每個節點的線性模型組合成的神經網絡模型也必然是線性的。這跟直接使用一個線性模型在效果上并沒有什么差異，模型能力不強，反而花費了更多不必要的力氣。所以一般來說，中間節點不會選擇線性模型。 如果每個節點的transformation function都是階梯函數（即sign()函數）。這是一個非線性模型，但是由于階梯函數是離散的，并不是處處可導，所以在優化計算時比較難處理。所以，一般也不選擇階梯函數作為transformation function。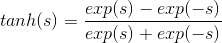 既然線性函數和階梯函數都不太適合作為transformation function，那么最常用的一種transformation function就是tanh(s)，其表達式如下：  tanh(s)函數是一個平滑函數，類似“s”型。當|s|比較大的時候，tanh(s)與階梯函數相近；當|s|比較小的時候，tanh(s)與線性函數比較接近。從數學上來說，由于處處連續可導，便于最優化計算。而且形狀上類似階梯函數，具有非線性的性質，可以得到比較復雜強大的模型。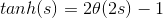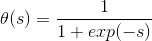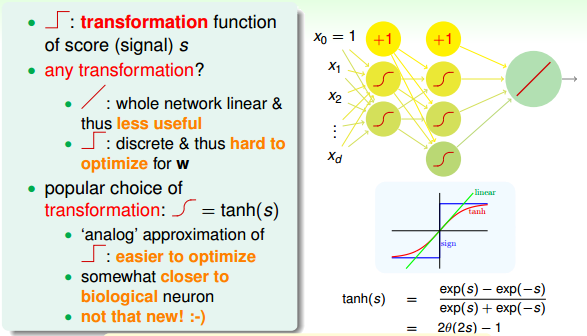 順便提一下，tanh(x)函數與sigmoid函數存在下列關系：  其中，   那么，接下來我們就使用tanh函數作為神經網絡中間層的transformation function，所有的數學推導也基于此。實際應用中，可以選擇其它的transformation function，不同的transformation function，則有不同的推導過程。 下面我們將仔細來看看Neural Network Hypothesis的結構。如下圖所示，該神經網絡左邊是輸入層，中間兩層是隱藏層，右邊是輸出層。整體上來說，我們設定輸入層為第0層，然后往右分別是第一層、第二層，輸出層即為第3層。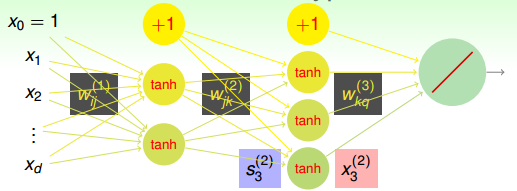  Neural Network Hypothesis中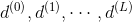，分別表示神經網絡的第幾層，其中L為總層數。例如上圖所示的是3層神經網絡，L=3。我們先來看看每一層的權重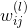，上標l滿足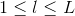，表示是位于哪一層。下標i滿足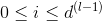，表示前一層輸出的個數加上bias項（常數項）。下標j滿足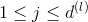，表示該層節點的個數（不包括bias項）。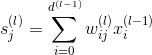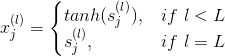 對于每層的分數score，它的表達式為：  對于每層的transformation function，它的表達式為：  因為是regression模型，所以在輸出層（l=L）直接得到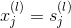。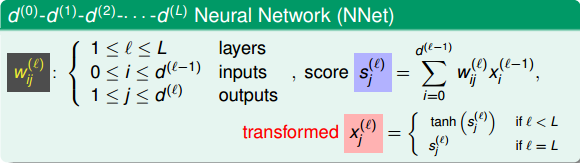  介紹完Neural Network Hypothesis的結構之后，我們來研究下這種算法結構到底有什么實際的物理意義。還是看上面的神經網絡結構圖，每一層輸入到輸出的運算過程，實際上都是一種transformation，而轉換的關鍵在于每個權重值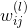。每層網絡利用輸入x和權重w的乘積，在經過tanh函數，得到該層的輸出，從左到右，一層一層地進行。其中，很明顯，x和w的乘積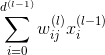越大，那么tanh(wx)就會越接近1，表明這種transformation效果越好。再想一下，w和x是兩個向量，乘積越大，表明兩個向量內積越大，越接近平行，則表明w和x有模式上的相似性。從而，更進一步說明了如果每一層的輸入向量x和權重向量w具有模式上的相似性，比較接近平行，那么transformation的效果就比較好，就能得到表現良好的神經網絡模型。也就是說，神經網絡訓練的核心就是pattern extraction，即從數據中找到數據本身蘊含的模式和規律。通過一層一層找到這些模式，找到與輸入向量x最契合的權重向量w，最后再由G輸出結果。  ### **Neural Network Learning** 我們已經介紹了Neural Network Hypothesis的結構和算法流程。確定網絡結構其實就是確定各層的權重值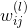。那如何根據已有的樣本數據，找到最佳的權重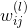使error最小化呢？下面我們將詳細推導。  首先，我們的目標是找到最佳的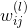讓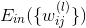最小化。如果只有一層隱藏層，就相當于是aggregation of perceptrons。可以使用我們上節課介紹的gradient boosting算法來一個一個確定隱藏層每個神經元的權重，輸入層到隱藏層的權重可以通過C&RT算法計算的到。這不是神經網絡常用的算法。如果隱藏層個數有兩個或者更多，那么aggregation of perceptrons的方法就行不通了。就要考慮使用其它方法。 根據error function的思想，從輸出層來看，我們可以得到每個樣本神經網絡預測值與實際值之間的squared error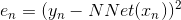：，這是單個樣本點的error。那么，我們只要能建立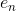與每個權重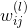的函數關系，就可以利用GD或SGD算法對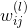求偏微分，不斷迭代優化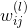值，最終得到使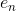最小時對應的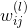。  為了建立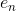與各層權重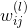的函數關系，求出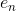對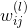的偏導數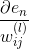，我們先來看輸出層如何計算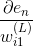。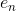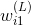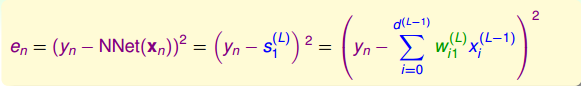與的函數關系為：  計算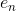對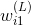的偏導數，得到：  以上是輸出層求偏導的結果。如果是其它層，即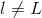，偏導計算可以寫成如下形式：  上述推導中，令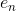與第l層第j個神經元的分數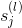的偏導數記為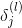。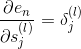即：  當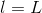時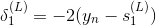，；當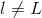時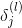，是未知的，下面我們將進行運算推導，看看不同層之間的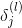是否有遞推關系。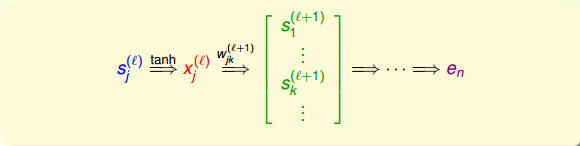  如上圖所示，第l層第j個神經元的分數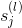經過tanh函數，得到該層輸出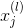，再與下一層權重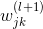相乘，得到第l+1層的分數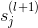，直到最后的輸出層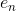。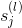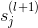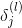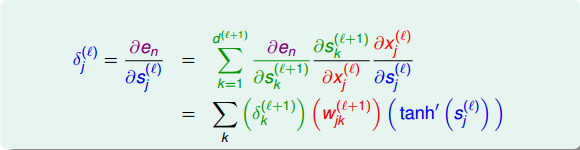 那么，利用上面到這樣的遞推關系，我們可以對偏導數做一些中間變量替換處理，得到如下表達式：  值得一提的是，上式中有個求和項，其中k表示下一層即l+1層神經元的個數。表明l層的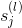與l+1層的所有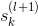都有關系。因為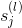參與到每個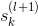的運算中了。 這樣，我們得到了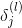與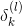的遞推關系。也就是說如果知道了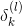的值，就能推導出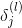的值。而最后一層，即輸出層的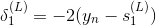，那么就能一層一層往前推導，得到每一層的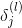，從而可以計算出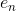對各個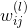的偏導數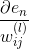。計算完偏微分之后，就可以使用GD或SGD算法進行權重的迭代優化，最終得到最優解。 神經網絡中，這種從后往前的推導方法稱為Backpropagation Algorithm，即我們常常聽到的BP神經網絡算法。它的算法流程如下所示：  上面采用的是SGD的方法，即每次迭代更新時只取一個點，這種做法一般不夠穩定。所以通常會采用mini-batch的方法，即每次選取一些數據，例如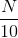，來進行訓練，最后求平均值更新權重w。這種做法的實際效果會比較好一些。 ### **Optimization and Regularization** 經過以上的分析和推導，我們知道神經網絡優化的目標就是讓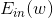最小化。本節課我們采用error measure是squared error，當然也可以采用其它的錯誤衡量方式，只要在推導上做稍稍修改就可以了，此處不再贅述。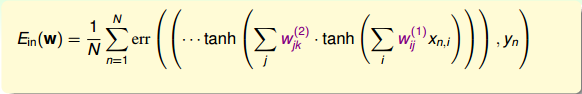  下面我們將主要分析神經網絡的優化問題。由于神經網絡由輸入層、多個隱藏層、輸出層構成，結構是比較復雜的非線性模型，因此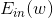可能有許多局部最小值，是non-convex的，找到全局最小值（globalminimum）就會困難許多。而我們使用GD或SGD算法得到的很可能就是局部最小值（local minimum）。 基于這個問題，不同的初始值權重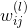通常會得到不同的local minimum。也就是說最終的輸出G與初始權重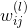有很大的關系。在選取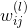上有個技巧，就是通常選擇比較小的值，而且最好是隨機random選擇。這是因為，如果權重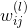很大，那么根據tanh函數，得到的值會分布在兩側比較平緩的位置（類似于飽和saturation），這時候梯度很小，每次迭代權重可能只有微弱的變化，很難在全局上快速得到最優解。而隨機選擇的原因是通常對權重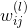如何選擇沒有先驗經驗，只能通過random，從普遍概率上選擇初始值，隨機性避免了人為因素的干預，可以說更有可能經過迭代優化得到全局最優解。  下面從理論上看一下神經網絡模型的VC Dimension。對于tanh這樣的transfer function，其對應的整個模型的復雜度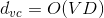。其中V是神經網絡中神經元的個數（不包括bias點）,D表示所有權值的數量。所以，如果V足夠大的時候，VC Dimension也會非常大，這樣神經網絡可以訓練出非常復雜的模型。但同時也可能會造成過擬合overfitting。所以，神經網絡中神經元的數量V不能太大。 為了防止神經網絡過擬合，一個常用的方法就是使用regularization。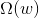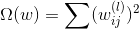之前我們就介紹過可以在error function中加入一個regularizer，例如熟悉的L2 regularizer ：  但是，使用L2 regularizer 有一個缺點，就是它使每個權重進行等比例縮小（shrink）。也就是說大的權重縮小程度較大，小的權重縮小程度較小。這會帶來一個問題，就是等比例縮小很難得到值為零的權重。而我們恰恰希望某些權重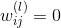，即權重的解是松散（sparse）的。因為這樣能有效減少VC Dimension，從而減小模型復雜度，防止過擬合發生。 那么為了得到sparse解，有什么方法呢？我們之前就介紹過可以使用L1 regularizer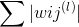：，但是這種做法存在一個缺點，就是包含絕對值不容易微分。除此之外，另外一種比較常用的方法就是使用weight-elimination regularizer。weight-elimination regularizer類似于L2 regularizer，只不過是在L2 regularizer上做了尺度的縮小，這樣能使large weight和small weight都能得到同等程度的縮小，從而讓更多權重最終為零。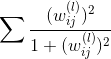weight-elimination regularizer的表達式如下：   除了weight-elimination regularizer之外，還有另外一個很有效的regularization的方法，就是Early Stopping。簡而言之，就是神經網絡訓練的次數t不能太多。因為，t太大的時候，相當于給模型尋找最優值更多的可能性，模型更復雜，VC Dimension增大，可能會overfitting。而t不太大時，能有效減少VC Dimension，降低模型復雜度，從而起到regularization的效果。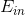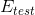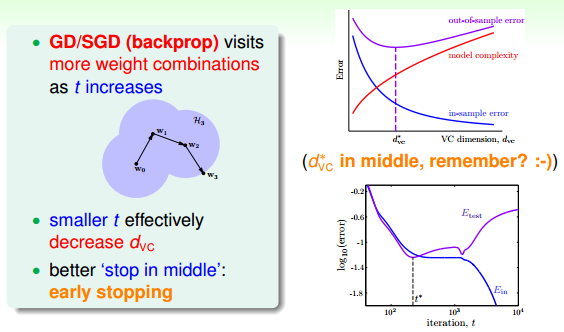和隨訓練次數t的關系如下圖右下角所示：  那么，如何選擇最佳的訓練次數t呢？可以使用validation進行驗證選擇。 ### **總結** 本節課主要介紹了Neural Network模型。首先，我們通過使用一層甚至多層的perceptrons來獲得更復雜的非線性模型。神經網絡的每個神經元都相當于一個Neural Network Hypothesis，訓練的本質就是在每一層網絡上進行pattern extraction，找到最合適的權重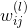，最終得到最佳的G。本課程以regression模型為例，最終的G是線性模型，而中間各層均采用tanh函數作為transform function。計算權重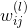的方法就是采用GD或者SGD，通過Backpropagation算法，不斷更新優化權重值，最終使得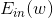最小化，即完成了整個神經網絡的訓練過程。最后，我們提到了神經網絡的可以使用一些regularization來防止模型過擬合。這些方法包括隨機選擇較小的權重初始值，使用weight-elimination regularizer或者early stopping等。 **_注明：_** 文章中所有的圖片均來自臺灣大學林軒田《機器學習技法》課程