# 前言 現在面試測試崗位，一般會要求熟悉一門語言（python/java），為了考驗求職者的基本功，一般會出2個筆試題，這些題目一般不難，主要考察基本功。 要是給你一臺電腦，在編輯器里面邊寫邊調試，沒多大難度。主要是給你一張紙和筆，讓你現場寫出來，那就沒那么容易了。 （本篇代碼都是基于python3.6） <br /> <details> <summary>1. 統計</summary> > 問題1：統計在一個隊列中的數字，有多少個正數，多少個負數，如\[1, 3, 5, 7, 0, -1, -9, -4, -5, 8\] #### 方法一 ~~~ # coding:utf-8 a = [1, 3, 5, 7, 0, -1, -9, -4, -5, 8] # 用列表生成式，生成新的列表 b = [i for i in a if i > 0] print("大于0的個數：%s" % len(b)) c = [i for i in a if i < 0] print("小于0的個數：%s" % len(c)) ~~~ #### 方法二 ~~~ # coding:utf-8 a = [1, 3, 5, 7, 0, -1, -9, -4, -5, 8] # 用傳統的判斷思維，累加 m = 0 n = 0 for i in a: if i > 0: m += 1 elif i < 0: n += 1 else: pass print("大于0的個數：%s" % m) print("小于0的個數：%s" % n) ~~~ </details> <br /> <details> <summary>2. 字符串切片</summary> > 問題1：字符串 "axbyczdj"，如果得到結果“abcd” #### 方法一 ~~~ # 字符串切片 a = "axbyczdj" print(a[::2]) ~~~ #### 方法二 ~~~ # 傳統思維 a = "axbyczdj" c = [] for i in range(len(a)): if i % 2 == 0: c.append(a[i]) print("".join(c)) ~~~ </details> <br /> <details> <summary>3. 字符串切割</summary> > 問題：已知一個字符串為“hello\_world\_yoyo”, 如何得到一個隊列 \["hello","world","yoyo"\] ~~~ a = "hello_world_yoyo" b = a.split("_") print(b) ~~~ </details> <br /> <details> <summary>4. 格式化輸出</summary> > 問題1：已知一個數字為1，如何輸出“0001” ~~~ a = 1 print("%04d" % a) ~~~ </details> <br /> <details> <summary>5. 隊列</summary> > 問題1：已知一個隊列,如： [1, 3, 5, 7], 如何把第一個數字，放到第三個位置，得到：[3, 5, 1, 7] ~~~ a = [1, 3, 5, 7] # insert插入數據 a.insert(3, a[0]) print(a[1:]) ~~~ </details> <br /> <details> <summary>6. 交換</summary> > 問題1：已知 a = 9, b = 8,如何交換a和b的值，得到a的值為8,b的值為9 #### 方法1 ~~~ a = 8 b = 9 a, b = b, a print(a) print(b) ~~~ #### 方法2 ~~~ a = 8 b = 9 # 用中間變量c c = a a = b b = c print(a) print(b) ~~~ </details> <br /> <details> <summary>7. 水仙花</summary> > 問題1：打印出100-999所有的"水仙花數"，所謂"水仙花數"是指一個三位數，其各位數字立方和等于該數本身。例如：153是一個"水仙花數"，因為153=1的三次方＋5的三次方＋3的三次方。 <br /> 方法一 ~~~ sxh = [] for i in range(100, 1000): s = 0 m = list(str(i)) for j in m: s += int(j)**len(m) if i == s: print(i) sxh.append(i) print("100-999的水仙花數：%s" % sxh) ~~~ <br /> 方法二 ``` sxh = [] for i in range(100,1000): s = str(i) if int(s[0])**3+int(s[1])**3+int(s[2])**3 == i: sxh.append(i) print(sxh) ``` </details> <br /> <details> <summary>8. 完全數</summary> > 問題1：如果一個數恰好等于它的因子之和，則稱該數為“完全數”，又稱完美數或完備數。 例如：第一個完全數是6，它有約數1、2、3、6，除去它本身6外，其余3個數相加， > 1+2+3=6。第二個完全數是28，它有約數1、2、4、7、14、28，除去它本身28外，其余5個數相加，1+2+4+7+14=28。 > 那么問題來了，求1000以內的完全數有哪些？ ~~~ a = [] for i in range(1, 1000): s = 0 for j in range(1, i): if i % j == 0 and j < i: s += j if s == i: print(i) a.append(i) print("1000以內完全數：%s" % a) ~~~ </details> <br /> <details> <summary>9. 冒泡排序</summary> > 冒泡排序（Bubble Sort）也是一種簡單直觀的排序算法。它重復地走訪過要排序的數列，一次比較兩個元素，如果他們的順序錯誤就把他們交換過來。走訪數列的工作是重復地進行直到沒有再需要交換，也就是說該數列已經排序完成。這個算法的名字由來是因為越小的元素會經由交換慢慢"浮"到數列的頂端。 問題1：用python寫個冒泡排序 * 方法一： ~~~ a = [1, 3, 10, 9, 21, 35, 4, 6] s = range(1, len(a))[::-1] print(list(s)) # 交換次數 for i in s: for j in range(i): if a[j] > a[j + 1]: a[j], a[j + 1] = a[j + 1], a[j] print("第 %s 輪交換后數據：%s" % (len(s)-i+1, a)) print(a) ~~~ * 方法二 ``` def bubbleSort(arr): n = len(arr) # 遍歷所有數組元素 for i in range(n): # 最后一個i元素已經存在 for j in range(0, n - i - 1): if arr[j] > arr[j + 1]: arr[j], arr[j + 1] = arr[j + 1], arr[j] arr = [1, 3, 10, 9, 21, 35, 4, 6] bubbleSort(arr) print("排序后的數組:") for i in range(len(arr)): print("%d" % arr[i]) ``` </details> <br /> <details> <summary>10. sort排序</summary> > 問題1：已知一個隊列\[1, 3, 6, 9, 7, 3, 4, 6\] * 按從小到大排序 * 按從大大小排序 * 去除重復數字 ~~~ a = [1, 3, 6, 9, 7, 3, 4, 6] # 1.sort排序，正序 a.sort() print(a) # 2.sort倒敘 a.sort(reverse=True) print(a) # 3.去重 b = list(set(a)) print(b) ~~~ </details> <br /> <details> <summary>11. 計算n的階乘</summary> > 問題1：計算n!,例如n=3(計算3*2*1=6)， 求10! #### 方法1：可以用python里面的reduce函數，reduce() 函數會對參數序列中元素進行累積。 函數將一個數據集合（鏈表，元組等）中的所有數據進行下列操作：用傳給 reduce 中的函數 function（有兩個參數）先對集合中的第 1、2 個元素進行操作，得到的結果再與第三個數據用 function 函數運算，最后得到一個結果。 ~~~ from functools import reduce # 方法1：推薦！ a = 10 b = reduce(lambda x, y: x*y, range(1, a+1)) print(b) ~~~ 如果不想用lamdba函數，可以定義一個函數 ~~~ from functools import reduce def chengfa(x, y): return x*y a = 10 b = reduce(chengfa, range(1, a+1)) print(b) ~~~ #### 方法2：自己寫個遞歸函數 ~~~ def digui(n): if n == 1: return 1 else: return n*digui(n-1) a = 10 print(digui(a)) ~~~ #### 方法3：用for循環（不推薦！） ~~~ a = 10 s = 1 for i in range(1, a+1): s = s*i print(s) ~~~ </details> <br /> <details> <summary>12. 斐波那契數列</summary> <br /> > 問題1：已知一個數列：1、1、2、3、5、8、13.....的規律為從3開始的每一項都等于其前兩項的和，這是斐波那契數列。求滿足規律的100以內的所有數據 ~~~ a = 0 b = 1 while b < 100: print(b, end=",") a, b = b, a+b ~~~ </details> <br /> <details> <summary>13. 冪的遞歸</summary> <br /> 計算x的n次方，如：3的4次方 為3\*3\*3\*3=81 ~~~ def mi(x, n): '''計算x 的n 次方''' if n == 0: return 1 else: return x*mi(x, n-1) x = 3 num = 4 print(mi(x, num)) ~~~ </details> <br /> <details> <summary>14. 漢諾塔問題(一般不會考)</summary> <br /> 漢諾塔：漢諾塔（又稱河內塔）問題是源于印度一個古老傳說的益智玩具。大梵天創造世界的時候做了三根金剛石柱子，在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。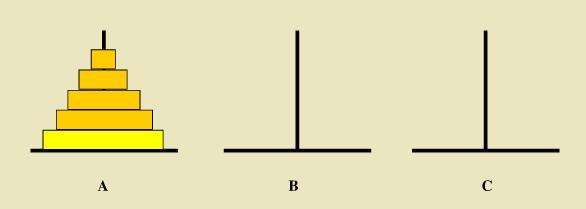并且規定，在小圓盤上不能放大圓盤，在三根柱子之間一次只能移動一個圓盤  當只有一個盤子的時候，只需要從將A塔上的一個盤子移到C塔上。 當A塔上有兩個盤子是，先將A塔上的1號盤子（編號從上到下）移動到B塔上，再將A塔上的2號盤子移動的C塔上，最后將B塔上的小盤子移動到C塔上。 當A塔上有3個盤子時，先將A塔上編號1至2的盤子（共2個）移動到B塔上（需借助C塔），然后將A塔上的3號最大的盤子移動到C塔，最后將B塔上的兩個盤子借助A塔移動到C塔上。 當A塔上有n個盤子是，先將A塔上編號1至n-1的盤子（共n-1個）移動到B塔上（借助C塔），然后將A塔上最大的n號盤子移動到C塔上，最后將B塔上的n-1個盤子借助A塔移動到C塔上。 綜上所述，除了只有一個盤子時不需要借助其他塔外，其余情況均一樣（只是事件的復雜程度不一樣）。 ~~~ def hanoi(n, a, b, c): '''漢諾塔問題''' if n == 1: print(a, '-->', c) else: hanoi(n - 1, a, c, b) print(a, '-->', c) hanoi(n - 1, b, a, c) hanoi(5, 'A', 'B', 'C') ~~~ 一般漢諾塔問題不會經常考，前面幾個考的比較頻繁 </details> <br /> <details> <summary>15. 對列表list去重</summary> <br /> 方法一：直接的方法 ``` old_list = [2, 3, 4, 5, 1, 2, 3] new_list = [] for i in old_list: if i not in new_list: new_list.append(i) print(new_list) # [2, 3, 4, 5, 1] ``` </details> <br /> <details> <summary>16. 如何判斷三角形的類型</summary> ``` a = int(input("請輸入第一條邊:")) b = int(input("請輸入第二條邊:")) c = int(input("請輸入第三條邊:")) if (a+b>c) and (a+c>b) and (b+c>a): if a==b==c: print("等邊三角形") elif (a==b or b==c or a==c): print("等腰三角形") elif (a*a + b*b == c*c) or (a*a + c*c == b*b) or (b*b + c*c == a*a): print("直角三角形") else: print("不規則三角形") else: print("不是三角形") ``` </details> <br />