感覺幾乎都是從這篇文章里找的：[https://blog.csdn.net/Hackbuteer1/article/details/6726419](https://blog.csdn.net/Hackbuteer1/article/details/6726419) [https://blog.csdn.net/bigpudding24/article/details/44198989](https://blog.csdn.net/bigpudding24/article/details/44198989) # 1.賽馬問題 一共有 25 匹馬，有一個賽場，賽場有 5 個賽道，就是說最多同時可以有5匹馬一起比賽。假設每匹馬都跑的很穩定，不用任何其他工具，只通過馬與馬之間的比賽，試問最少得比多少場才能知道跑得最快的5匹馬。 參考答案：[答案](https://hxraid.iteye.com/blog/662643) # 2.握手問題 5 對夫妻互相握手，有 1 人發現除他自己外其他人的握手次數各不相同（他自己可以與其中任何一人的握手次數相同），問這個人的握手次數？ 條件：① 夫妻之間不能握手 ② A 和 B 握手后不能再次握手 參考答案：一共 10 人，每人握手次數為 0 ~ 9 假設一對夫妻中有 1 人握手次數為 8，那么其他人肯定與他握了 1 次手（握手次數大于等于 1），那么其妻子的握手次數肯定為 0；依次類推，得到以下握手次數的組合 8 | 0  7 | 1  6 | 2   5 | 3  4 | 4 所以發現的人肯定是握手了 4 次的 # 3.倒水問題 一個 3 升的桶和一個 5 升的桶最后怎么裝 4 升的水？ 答：5 升滿上倒入 3 升桶里，5 升桶剩 2 升；3 升桶倒光，2 升倒入 3 升桶，5 升桶再滿上倒入 1 升到 3 升桶中 # 4.天平秤重 有 16 個球，一個是次品，次品比較輕，利用天平，至少幾次保證能找到次品？ 參考答案：3 次 第一次：兩邊一次各放 5 個，較輕的，次品就在里面，如果平衡，則次品在剩下的 6 個里面 第二次：情況 1，如果在上面 5 個堆里，兩邊各放 2 個，較輕的，次品就在里面；如果平衡，則次品就是剩下一個 ；情況 2，如果在上面 6 個堆里，兩邊各放 2 個，較輕的，次品就在里面；如果平衡，則次品就是剩下 2 個中的一個 第三次：再拿有次品的兩個放在天平上，較輕的就是次品 綜上所述，16 個球稱三次就可以保證找到次品 # 5.矩陣分為同樣大小的正方形 把如圖的長方形分成若干個同樣大小的正方形，要使正方形盡可能大，那么正方形的邊長最長是多少？  **分析**：分成同樣大小，且沒有剩余，就是分成的小正方形的邊長是 48 和 30 的公因數，要使正方形盡可能大，就是以 48 和 30 的最大公因數為小正方形的邊長． **解答**：解：48=2×2×2×2×3， 30=2×3×5， 所以 48 和 30 的最大公因數是：2×3=6；，即小正方形的邊長是 6 厘米． 答：正方形的邊長最長是 6cm． 附：求最大公約數 [輾轉相除法](https://baike.baidu.com/item/%E8%BE%97%E8%BD%AC%E7%9B%B8%E9%99%A4%E6%B3%95/4625352?fr=aladdin) # 6.任意時間求時針與分針的夾角 設 12 時的刻度線為 0 度,作為角度起點線, 任意時刻 X 時 Y 分時的兩針位置： 因為分針每分鐘轉 360 / 60＝6° 時針每分鐘轉 360 / (12\*60)＝ 0.5° 時針每 1 小時轉 360 / 12＝30° 所以, 在 X 時 Y 分時,時針與 0 度起點線的夾角（轉過角）是：30X＋0.5Y 在 X 時 Y 分時,分針與 0 度起點線的夾角（轉過角）是：6Y 時針和分針夾角 θ 的計算公式是： θ = |6Y - (30X + 0.5Y)| = |5.5Y - 30X|，單位是度（°） 習慣上，超過 180° 的角度一般用它的小于 180° 的角度（360° - |5.5Y - 30X|）表示它們的夾角. 例如：8:30 時的兩針夾角：將 X＝8,Y＝30 代入上式,得夾角＝75° . # 7.海盜分金幣問題 轉自 [https://blog.csdn.net/csdnsevenn/article/details/86522861](https://blog.csdn.net/csdnsevenn/article/details/86522861) 海盜分金幣問題： 有 5 個海盜，獲得了 100 枚金幣，于是他們要商量一個方法來分配金幣。商議方式如下： 1\. 由 5 個海盜輪流提出分配方案。 2\. 如果超過半數海盜（包括提出者）同意該方案，則按照該方案分配。 3\. 如果同意該方案的人數（包括提出者）小于等于半數，則提出者要被扔到海里喂魚，剩下的海盜繼續商議分配。 4\. 海盜們都是絕對理性的，以自己盡可能多獲得金幣為目的。但是在收益相等的情況下，會傾向把提出者扔到海里。 問：第一個海盜應該提出怎樣的分配方案，才能保證自己既不被扔到海里，又能使自己利益最大化？ ***** 這個問題需要用遞歸的思想來解決： 我們把五個海盜簡稱為老一、老二、老三、老四、老五。 老一在提出分配方案的時候，不妨這樣思考： 如果我被扔到海里了，剩下**4**個海盜，此時老二的最優分配方案是什么呢？ 我只要在老二的分配方案上稍微增加一點，就能贏得更多的支持。 老二在提出分配方案的時候，也會這樣思考： 如果我被扔到海里了，剩下**3**個海盜，此時老三的最優分配方案是什么呢？ 我只要在老三的分配方案上稍微增加一點，就能贏得更多的支持。 老三在提出分配方案的時候，還是會這樣思考： 如果我被扔到海里了，剩下**2**個海盜，此時老四的最優分配方案是什么呢？ 我只要在老四的分配方案上稍微增加一點，就能贏得更多的支持。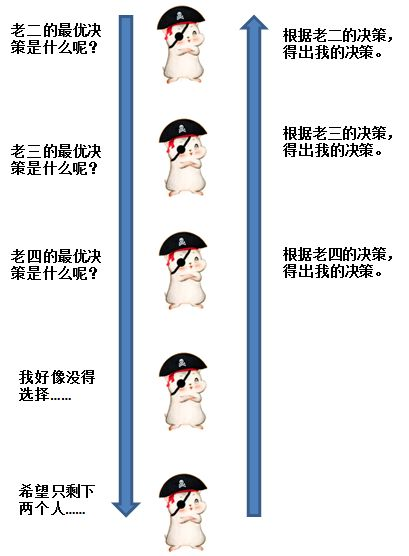 整個遞歸過程，就像下圖一樣：  這個遞歸過程到什么時候截止呢？剩下兩個人為止。 想想看，當剩下兩個人的時候，是什么情形？ 此時老四**沒有任何選擇**！無論他如何分配，哪怕把100枚金幣都給老五，老五仍然可以反對，導致老四被扔到海里，金幣全歸老五所有。  由此，老三心想：老四沒有最優決策，所以無論我提出什么要求，老四都一定會同意，而老五一定不同意。 由于只要超過半數同意就可以執行分配，所以老三的最優策略如下：  接下來，老二暗自尋思：如果沒有我，老三能獲得100枚金幣，所以無論如何不會同意我。但我可以設法“籠絡”老四和老五，形成 3 : 1 的局面。 在老三的“淫威”下，他們原本一個金幣都得不到。我給他們一人一枚金幣，好過由老三來分配，所以他們肯定會同意。 因此，老二的最優策略如下：  終于輪到老一了，老一心里琢磨：如果沒有我，老二能獲得 98 枚金幣，我總不能分給他多于 98 枚，索性放棄他，只要剩下三人中籠絡到兩人，形成 3 : 2 的局面即可。 要籠絡誰呢？以老二的策略，老三得不到金幣，所以老三最好“伺候”。我給老三 1 枚，老三一定同意。 至于老四和老五，本來可以得到 1 枚，所以我必須比老二給的多，才能贏得支持。但我又沒必要同時籠絡他倆，要么給老四兩枚金幣，放棄老五，要么給老五兩枚金幣，放棄老四。 因此，老一的最優策略如下：