排序算法及常見問題 · 前端小冊

[TOC] # 排序推薦閱讀 [掘金-排序算法總結](https://juejin.im/post/57dcd394a22b9d00610c5ec8#heading-27) 排序算法性能分析的指標：**關鍵碼的比較次數**，**記錄交換次數**。穩定性：如果一種排序算法不會改變關鍵碼值相同的記錄的相對順序，則稱其為穩定的 ## 冒泡排序依次比較、交換相鄰的元素，每輪將一個最大的元素“冒泡”到最后(第i位置) ```javaScript // 公共方法；以下均假設實現升序排列 function swap(arr, index1, index2) { let tmp = arr[index1] arr[index1] = arr[index2] arr[index2] = tmp } ``` ```javaScript function bubbleSort(arr) { for(let i = arr.length - 1; i > 0; i--) { for (let j = 0; j < i; j++) { if (arr[j] > arr[j+1]) { swap(arr, j, j+1) } } } } ``` ## 選擇排序每一次內循環遍歷尋找最小的數，記錄下 minIndex，并在這次內循環結束后交換 minIndex 和 i 的位置。重復這樣的循環 n - 1 次即得到結果。 ```javaScript function selectionSort(arr) { for (let i = 0, len = arr.length; i < len - 1; i++) { let minIndex = i for (let j = i+1; j < len; j++) { if (arr[j] < arr[minIndex]) { minIndex = j } } swap(arr, i, minIndex) } } ``` ## 插入排序：逐個處理待排序的記錄。每個新記錄與前面已排序的子記錄比較，將其插入到子序列正確的位置 ```javaScript function insertSort(arr) { for (let i = 1; i < arr.length; i++) { for (let j = i; j > 0; j--) { if (arr[j] < arr[j-1]) { swap(arr, j, j-1) } } } } ``` ## 希爾排序先將整個待排序的記錄序列分割成為若干子序列分別進行直接插入排序，具體算法描述： - 選擇一個增量序列 t1，t2，…，tk，其中 ti > tj，tk = 1； - 按增量序列個數 k，對序列進行 k 趟排序； - 每趟排序，根據對應的增量 ti，將待排序列分割成若干長度為 m 的子序列，分別對各子表進行直接插入排序。僅增量因子為1 時，整個序列作為一個表來處理，表長度即為整個序列的長度。 ![](https://img.kancloud.cn/6d/02/6d02254416ae04b1b3f586b250a0225b_480x469.png =400x) ```js function shellSort (arr) { let N = arr.length // 最開始時的增量 gap 為數組長度的一半 for (let gap = Math.floor(N / 2); gap > 0; gap = Math.floor(gap / 2)) { // 對各個分組進行插入排序 for (let i = gap; i < N; i++) { // 將 arr[i] 插入到所在分組正確的位置上 insertI(arr, gap, i) } } } function insertI (arr, gap, i) { let inserted = arr[i] let j for (j = i - gap; j >=0 && inserted < arr[j]; j -= gap) { arr[j + gap] = arr[j] } arr[j + gap] = inserted } ``` ## 歸并排序 2路歸并排序：歸并排序（劃分過程）用遞歸實現。若當前（未排序）序列的長度不大于1 返回當前序列否則，將當前未排序序列分割為大小相等的兩個子序列，分別用歸并排序對兩個子序列進行排序，將返回的兩個有序子序列**合并**成一個有序序列 ```javaScript function mergeSort(arr) { const len = arr.length if (len < 2) { return arr } const mid = Math.floor(len / 2) const left = arr.slice(0, mid) const right = arr.slice(mid) return merge(mergeSort(left), mergeSort(right)) } function merge(left, right) { const result = [] // 注意長度限制 while (left.length > 0 && right.length > 0) { result.push(left[0] <= right[0] ? left.shift() : right.shift()) } return result.concat(left, right) // 注意合并剩下的 } ``` ## 快速排序算法思想：若當前（未排序）序列的長度不大于1 返回當前序列。否則，在待排序記錄中選取一個記錄做為**軸值(pivot)**，通過**劃分算法**將其余待排記錄劃分成兩部分，比P小的記錄放在P之前，比P大的記錄放在P之后；分別用快速排序對前后兩個子序列進行排序（注意軸值已經在最終排序好的數組中的位置,無須繼續處理） **非標準版本** ```javaScript function quickSort(arr) { const pivot = arr[0] const left = [] const right = [] if (arr.length < 2) { return arr } for (let i = 1, len = arr.length; i < len; i++) { arr[i] < pivot ? left.push(arr[i]) : right.push(arr[i]) } return quickSort(left).concat([pivot], quickSort(right)) } ``` **單循環版本？** ``` javaScript function quickSort(arr, left = 0, right = arr.length - 1) { if (left < right) { const pivot = partition(arr, left, right); quickSort(arr, left, pivot - 1); quickSort(arr, pivot + 1, right); } return arr; } function partition (arr, left ,right) { let pivot = left; // 以第一個元素為 pivot for (let i = left + 1; i <= right; i++) { if (arr[i] < arr[left]) { swap(arr, i, pivot); pivot += 1; } } swap(arr, left, pivot); //將 pivot 值移至中間 return pivot; } ``` **不知道啥版本** ```javaScript function partition(arr, left, right, pivotValue) { do { while (arr[++left] < pivotValue); // 注意加分號表示沒有循環體 while((left < right) && arr[--right] > pivotValue); swap(arr, left, right) } while (left < right) return left // 返回右半部分的第一個元素的下標 } // left, right視為數組的下標 function quickSort(arr, left, right) { if (left >= right) return // 1個元素不需要再劃分 let pivotindex = Math.floor((left + right) / 2) // 選取軸值，可以考慮隨機選取 swap(arr, pivotindex, right) // 把軸值與當前數組末尾元素交換 let k = partition(arr, left-1, right, arr[right]) // 劃分數組，返回軸值位置 swap(arr, k, right) // 把軸值換回來 // 注意k位置已經固定 quickSort(arr, left, k-1) quickSort(arr, k+1, right) } let myArray = [11, 81, 92, 72, 43, 53, 64, 34, 25, 16] let myArray2 = [5, 5, 3, 2, 6, 4, 5] quickSort(myArray2, 0, myArray2.length - 1) quickSort(myArray, 0, myArray.length - 1) console.log(myArray) console.log(myArray2) ``` 最后一個版本是我學數據結構課的書上的，還有那時候畫的圖，這是對[11, 81, 92, 72, 43, 53, 64, 34, 25, 16]的第一輪快速排序的流程圖 ![](https://box.kancloud.cn/fc6bc5fbd4afd0935ec5d784ae0721e0_726x687.png) ## 堆排序堆排序利用了二叉堆的特性來做，二叉堆通常用數組表示，并且二叉堆是一顆完全二叉樹（所有葉節點（最底層的節點）都是從左往右順序排序，并且其他層的節點都是滿的）。二叉堆又分為大根堆與小根堆。 * 大根堆是某個節點的所有子節點的值都比他小 * 小根堆是某個節點的所有子節點的值都比他大堆排序的原理就是組成一個大根堆或者小根堆。以小根堆為例，某個節點的左邊子節點索引是`i * 2 + 1`，右邊是`i * 2 + 2`，父節點是`(i - 1) /2`。算法思路： <1>.將初始待排序關鍵字序列(R1,R2....Rn)構建成大頂堆，此堆為初始的無序區； <2>.將堆頂元素R[1]與最后一個元素R[n]交換，此時得到新的無序區(R1,R2,......Rn-1)和新的有序區(Rn),且滿足R[1,2...n-1]<=R[n]； <3>.由于交換后新的堆頂R[1]可能違反堆的性質，因此需要對當前無序區(R1,R2,......Rn-1)調整為新堆，然后再次將R[1]與無序區最后一個元素交換，得到新的無序區(R1,R2....Rn-2)和新的有序區(Rn-1,Rn)。不斷重復此過程直到有序區的元素個數為n-1，則整個排序過程完成。 ```javaScript function heapSort(arr) { let size = arr.length; // 初始化堆，i 從最后一個父節點開始調整，直到節點均調整完畢 for (let i = Math.floor(size / 2) - 1; i >= 0; i--) { heapify(arr, i, size); } // 堆排序：每輪將堆頂元素和最后一個元素交換，然后重新調整堆 for (let i = size - 1; i > 0; i--) { swap(arr, 0, i); size -= 1; heapify(arr, 0, size); } return arr; } // 參數：數組，父結點下標，數組大小 function heapify(arr, index, size) { let largest = index; let left = 2 * index + 1; let right = 2 * index + 2; // 如果左子結點的值比父結點大則互換 if (left < size && arr[left] > arr[largest]) { largest = left; } // 如果右子結點的值比父結點的值大則互換 if (right < size && arr[right] > arr[largest]) { largest = right; } // 如果發生了互換，對父結點再次做堆特性的判斷 if (largest !== index) { swap(arr, index, largest); heapify(arr, largest, size); } } // test const arr = [91, 60, 96, 7, 35, 65, 10, 65, 9, 30, 20, 31, 77, 81, 24]; console.log(heapSort(arr)); ``` ## 桶排序算法思想：先將數組分到有限個桶中（根據映射函數），再對每個桶中的數據進行排序，對每個桶中數據的排序可以是桶排序的遞歸，或其他算法，在桶中數據較少的時候用插入排序最為理想。 ```js /** * * @param {arr} arrry 待排序數組 * @param {Number} num 桶的數量 */ function bucketSort (arr, num) { if (arr.length <= 1) return arr let len = arr.length, buckets = [], result = [], min = max = arr[0], regex = '/^[1-9]+[0-9]*$/', space, n = 0 num = num || ((num > 1 && regex.test(num)) ? num : 10) for (let i = 1; i < len; i++) { min = min <= arr[i] ? min : arr[i] max = max >= arr[i] ? max : arr[i] } space = (max - min + 1) / num for (let j = 0; j < len; j++) { let index = Math.floor((arr[j] - min) / space) // 映射函數 if (buckets[index]) { // 非空桶，插入排序 let k = buckets[index].length - 1 while (k >= 0 && buckets[index][k] > arr[j]) { buckets[index][k + 1] = buckets[index][k] k-- } buckets[index][k + 1] = arr[j] } else { // 空桶，初始化 buckets[index] = [] buckets[index].push(arr[j]) } } while (n < num) { result = result.concat(buckets[n]) n++ } return result } var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48] console.log(bucketSort(arr,4)) // [ 2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50 ] ``` ## 時間復雜度及適用情況分析 **插入排序：** 最適合于已經有一定順序的元素排列 - 最佳情況：輸入數組按升序排列。T(n) = O(n) - 最壞情況：輸入數組按降序排列。T(n) = O(n^2) - 平均情況：T(n) = O(n^2) **歸并排序：** 以空間換時間 - 最差情況：T(n) = O(nlogn) - 最優情況：T(n) = O(nlogn) - 平均情況：T(n) = O(nlogn) **快速排序：** 最好情況：Partition函數每次恰好能均分序列；?最壞情況：每次劃分只能將序列分為一個元素與其他元素兩部分，這時的快速排序退化為冒泡排序。 * 最佳情況：T(n) = O(nlogn) * 最差情況：T(n) = O(n^2) * 平均情況：T(n) = O(nlogn) **堆排序：** 時間復雜度分析：建堆：O(n) ； n次取堆的最大元素：O(log n) ；堆排序的總時間代價：O(2nlog n) * 最佳情況：T(n) = O(nlogn) * 最差情況：T(n) = O(nlogn) * 平均情況：T(n) = O(nlogn) | 算法 | 穩定性 | 時間復雜度 | 空間復雜度 | 備注 | | :-: | :-: | :-: | :-: | :-: | | 選擇排序 | × | N2 | 1 | | | 冒泡排序 | √ | N2 | 1 | | | 插入排序 | √ | N ~ N2 | 1 | 時間復雜度和初始順序有關 | | 希爾排序 | × | N 的若干倍乘于遞增序列的長度 | 1 | 改進版插入排序 | | 快速排序 | × | NlogN | logN | | | 三向切分快速排序 | × | N ~ NlogN | logN | 適用于有大量重復主鍵 | | 歸并排序 | √ | NlogN | N | | | 堆排序 | × | NlogN | 1 | 無法利用局部性原理 | # 查找 ## 二分查找 ```js // 二分查找，數組必須是有序的 function BinarySearch (arr, target) { let low = 0 let high = arr.length - 1 while (low <= high) { mid = Math.floor((low + high) / 2) if (arr[mid] === target) return mid if (arr[mid] < target) { low = mid + 1 } else { high = mid - 1 } } return -1 } ``` # 其他常見算法題 ## 全排列 [https://www.cnblogs.com/sooner/p/3264882.html](https://www.cnblogs.com/sooner/p/3264882.html) ```javaScript function swap(arr, index1, index2) { let tmp = arr[index1] arr[index1] = arr[index2] arr[index2] = tmp } // 重復元素不交換 function isSwap(arr, nBegin, nEnd) { for(let i = nBegin; i < nEnd; i++) { if (arr[i] === arr[nEnd]) { return false } } return true } /** * * @param {*} arr 數組 * @param {*} cur 當前待交換的數的下標 * @param {*} n 末尾下標 */ let cnt = 0 function permutation(arr, cur, n) { if (cur === n-1) { cnt++ let str = '' arr.forEach((item, index) => { str+=item }) console.log(`第${cnt}個全排列: ${str}`) } else { for (let i = cur; i < n; i++) { if (isSwap(arr, cur, i)) { swap(arr, cur, i) permutation(arr, cur+1, n) swap(arr, cur, i) } } } } let arr = [1, 3, 5] permutation(arr, 0, arr.length) /* 135 153 315 351 531 513 */ ``` ## 最大公約數 ```js // 輾轉相除 function gcd (a, b) { let c = a % b while (c !== 0) { a = b b = c c = a % b } return b } /* 319 % 377 = 0 (余 319) 377 % 319 = 1 (余 58) 319 % 58 = 5 (余 29) 58 % 29 = 2 (余 0) 所以 (319, 377) 的最大公約數為 29 */ // or function gcd (a, b) { return a % b === 0 ? 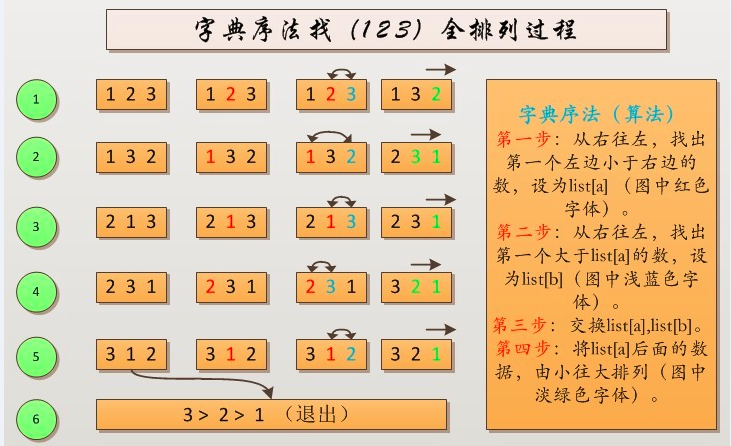b : gcd(b, a % b) } ``` ## 字典序算法 ![](https://img.kancloud.cn/2c/aa/2caaee79388ecde42155c615e41719d9_731x446.png) ```js function swap (arr, index1, index2) { let temp = arr[index1] arr[index1] = arr[index2] arr[index2] = temp } function Prim (arr) { let len = arr.length let indexFirst, indexSecond // 1 * 2 * 3 * ... n 個排列 let num = 1 for (let i = 1; i <= len; i++) { num *= i } num-- // 不算 123 了 while (num --) { // step1: 從右往左，找出第一個左邊小于右邊的數，記為 list[a] for (let i = len - 1; i > 0; i--) { if (arr[i - 1] < arr[i]) { indexFirst = i - 1 break } } // step2：從右往左，找出第一個大于 list[a] 的數，記為 list[b] for (let i = len - 1; i > 0; i--) { if (arr[i] > arr[indexFirst]) { indexSecond = i break } } // step3：交換 list[a] list[b]，將原先 list[a] 后面的數據(不包過 list[a])從小到大排列 swap(arr, indexFirst, indexSecond) // [1, 3, 2] -> [] arr = arr.slice(0, indexFirst + 1).concat(arr.slice(indexFirst + 1).sort()) console.log(arr.join('')) } } Prim([1, 2, 3]) /** * 132 * 213 * 231 * 312 * 321 */ ``` ## 回文字符串回文字符串：一個字符串，不論是從左往右，還是從右往左，字符的順序都是一樣的（如 abba，abcba 等）判斷回文字符串比較簡單，即用兩個變量 left，right 模仿指針（一個指向第一個字符，一個指向最后一個字符），每比對成功一次，left 向右移動一位，right 向左移動一位，如果 left 與 right 所指的元素不相等則退出，最后比較 left 與 right 的大小，如果 left > right 則說明是回文字符串。 ## Ksum 問題參考：[https://blog.csdn.net/haolexiao/article/details/70768526#commentBox](https://blog.csdn.net/haolexiao/article/details/70768526#commentBox) 在一個數組中，找出 K 個數相加和等于給定的數，這個叫做 Ksum 問題。在 leetcode 中有以下幾個題都是與之相關的 [two-sum](https://leetcode.com/problems/two-sum/) [3Sum](https://leetcode.com/problems/3sum/#/description) [3Sum Closest](https://leetcode.com/problems/3sum-closest/#/description) [4Sum](https://leetcode.com/problems/4sum/#/description) [4Sum II](https://leetcode.com/problems/4sum-ii/#/description) 2Sum 從數組中找出相加和為給定的數，有兩種思路： 1. 將數組排序，設置首尾兩個指針往中間走，直到得到滿足條件的解或指針相遇 2. 對數組中每個數建立一個 hashmap，然后再掃描一遍數組，判斷 target - nums[i] 是否存在第一種方法的時間復雜度為 O(nlogn)，主要是排序所花費的時間第二種方法的時間復雜度為 O(n) 3Sum 這個問題也有兩種思路： 1. 最外層遍歷一遍，轉換為 2Sum 問題 2. 另一種思路是，先預處理一遍數組中兩兩相加的結果，然后遍歷每一個數`nums[i]`，判斷`target-nums[i]`是否在預處理的那個和中兩種方法的時間復雜度都為 O(n^2) 3Sum Closest 這次要找的是最接近給定值的三個數之和，跟 3Sum 類似，只不過需要定一個 diff 變量來記錄差的絕對值 4Sum 這個問題也有兩種思路： 1. 先遍歷第一個數，然后固定第一個數之后，轉化為剩下元素的 3Sum 問題 2. 先遍歷兩個數，求和，然后轉化為剩下元素的 2Sum 問題