# 2 可視化數據：將數據映射到美學上 > 原文： [2 Visualizing data: Mapping data onto aesthetics](https://serialmentor.com/dataviz/aesthetic-mapping.html) > 校驗：[飛龍](https://github.com/wizardforcel) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 每當我們可視化數據時，我們都會采用數據值并將它們以系統和邏輯的方式轉換為構成最終圖形的視覺元素。盡管存在許多不同類型的數據可視化，并且乍一看散點圖，餅圖和熱圖似乎沒有太多共同點，但所有這些可視化都可以用一種通用語言來描述，它捕獲了數據如何變成紙上的墨水斑點，或屏幕上的彩色像素。主要的見解如下：所有數據可視化將數據值映射到所得圖形的可量化特征。我們將這些特征稱為美學。 ## 2.1 美學和數據類型 美學描述了給定圖形元素的每個方面。圖 2.1 中提供了一些示例。每個圖形元素的關鍵成分當然是它的位置，描述了元素的位置。在標準 2D 圖形中，我們通過`x`和`y`值來描述位置，但是其他坐標系和一維或三維可視化也是可能的。接下來，所有圖形元素都具有形狀，尺寸和顏色。即使我們正在制作黑白繪圖，圖形元素也需要有可見的顏色，例如，如果背景為白色，則為黑色；如果背景為黑色，則為白色。最后，我們使用線條來可視化數據，這些線條可能具有不同的寬度或點劃線圖案。除了圖 2.1 中顯示的示例之外，我們在數據可視化中可能會遇到許多其他美學。例如，如果我們想要顯示文本，我們可能必須指定字體系列，字體界面和字體大小，如果圖形對象重疊，我們可能必須指定它們是否部分透明。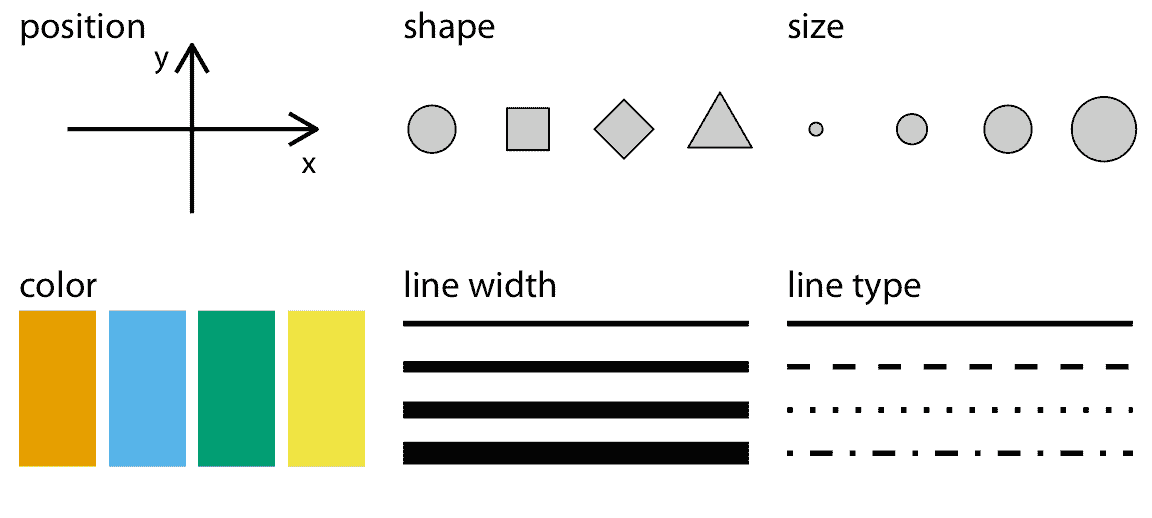  圖 2.1：數據可視化中常用的美學：位置，形狀，大小，顏色，線寬，線型。這些美學中的一些可以表示連續和離散數據（位置，大小，線寬，顏色），而其他美學通常僅表示離散數據（形狀，線型）。 所有美學都屬于兩類：可以代表連續數據的那些和不能代表連續數據的那些。連續數據值是存在任意精細中間體的值。例如，持續時間是連續值。在任何兩個持續時間（例如 50 秒和 51 秒）之間，存在任意多個中間體，例如 50.5 秒，50.51 秒，50.50001 秒等。相比之下，房間中的人數是離散值。一個房間可以容納 5 人或 6 人，但不能容納 5.5 人。對于圖 2.1 中的示例，位置，大小，顏色和線寬可以表示連續數據，但形狀和線型通常只能表示離散數據。 接下來，我們將考慮可能要在可視化中表示的數據類型。您可能會將數據視為數字，但數字只是我們可能遇到的幾種數據類型中的兩種。除連續和離散數值外，數據還可以以離散類別的形式，以日期或時間的形式出現，也可以作為文本（表 2.1）。當數據是數字時我們也稱它為定量的，當它是類別時我們稱它為定性的。保存定性數據的變量是因子，不同的類別稱為水平。最常見的一個因子的水平是沒有順序的（如表 2.1 中的“狗”，“貓”，“魚”的例子），但是當存在內在因素時也可以在水平之間的對因子排序（如表 2.1 中的“好”，“一般”，“差”的例子）。 表 2.1：典型數據可視化方案中遇到的變量類型。 | 變量的類型 | 例子 | 適當的刻度 | 描述 | | :-- | :-- | :-- | :-- | | 定量/數值連續 | `1.3, 5.7, 83, 1.5x10^(-2)` | 連續 | 任意數值。這些可以是整數，有理數或實數。 | | 定量/數值離散 | `1, 2, 3, 4` | 離散 | 離散單位中的數字。這些最常見但不一定是整數。例如，如果給定數據集中不存在中間值，則數字`0.5, 1.0, 1.5`也可視為離散。 | | 定性/無序類別 | 狗，貓，魚 | 離散 | 沒有順序的類別。這些是離散且唯一的類別，沒有固有的順序。這些變量也稱為因子。 | | 定性/有序類別 | 好，一般，差 | 離散 | 帶順序的類別。這些是具有順序的離散且唯一的類別。例如，“一般”總是介于“好”和“差”之間。這些變量也稱為有序因子。 | | 日期或時間 | 2018 年 1 月 5 日，上午 8:03 | 連續或離散 | 特定日期和/或時間。也可能是通用日期，例如 7 月 4 日或 12 月 25 日（沒有年份）。 | | 文本 | `The quick brown fox jumps over the lazy dog.` | 無或離散 | 自由格式的文本。如果需要，可以視為類別。 | 要查看這些不同類型數據的具體示例，請查看表 2.2 。它顯示了數據集的前幾行，它們提供了美國四個地點的日平均氣溫（30 年窗口中的平均日常溫度）。此表包含五個變量：月，日，位置，站點 ID 和溫度（以華氏度為單位）。月是有序因子，日是離散數值，位置是無序因子，站點 ID 同樣是無序因子，溫度是連續數值。 表 2.2：數據集的前 12 行，列出了四個氣象站的日平均氣溫。 數據來源：NOAA。 | 月 | 日 | 地點 | 站點 ID | 溫度 | | :-: | :-: | :-- | :-: | :-: | | Jan | 1 | Chicago | USW00014819 | 25.6 | | Jan | 1 | San Diego | USW00093107 | 55.2 | | Jan | 1 | Houston | USW00012918 | 53.9 | | Jan | 1 | Death Valley | USC00042319 | 51.0 | | Jan | 2 | Chicago | USW00014819 | 25.5 | | Jan | 2 | San Diego | USW00093107 | 55.3 | | Jan | 2 | Houston | USW00012918 | 53.8 | | Jan | 2 | Death Valley | USC00042319 | 51.2 | | Jan | 3 | Chicago | USW00014819 | 25.3 | | Jan | 3 | San Diego | USW00093107 | 55.3 | | Jan | 3 | Death Valley | USC00042319 | 51.3 | | Jan | 3 | Houston | USW00012918 | 53.8 | ## 2.2 將地圖數據值縮放到美學上 為了將數據值映射到美學上，我們需要指定哪些數據值對應于哪些特定的美學值。例如，如果我們的圖形具有 *x* 軸，那么我們需要指定哪些數據值沿著該軸落在特定位置上。同樣，我們可能需要指定哪些數據值由特定形狀或顏色表示。數據值和美學值之間的映射是通過刻度創建的。刻度定義了數據和美學之間的唯一映射（圖 2.2）。重要的是，刻度必須是一對一的，這樣對于每個特定的數據值，只有一個美學值，反之亦然。如果刻度不是一對一的，那么數據可視化就變得模棱兩可。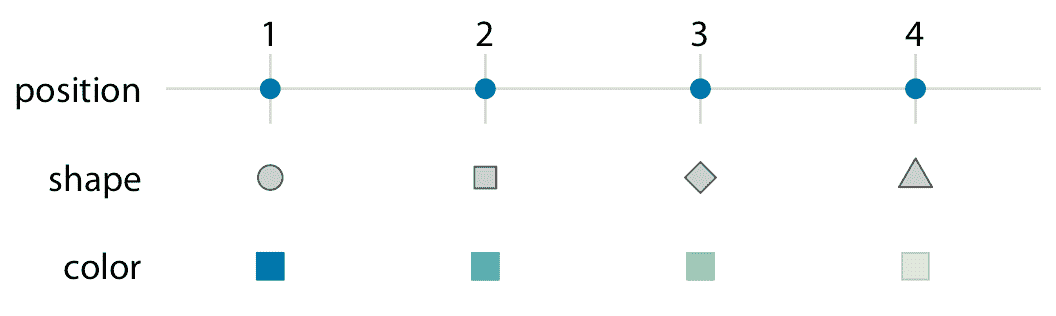  圖 2.2：將一串數據值縮放到美學。這里，數字 1 到 4 已被映射到位置，形狀和顏色刻度。對于每個刻度，每個數字對應于唯一的位置，形狀或顏色，反之亦然。 讓我們把事情付諸實踐。我們可以采用表 2.2 中顯示的數據集，將溫度映射到 *y* 軸上，一年中的日期映射到 *x* 軸上，位置映射到顏色上，并可視化這些美學與實線。結果是一個標準線圖，顯示了四個位置隨著日期的變化的平均氣溫（圖 2.3）。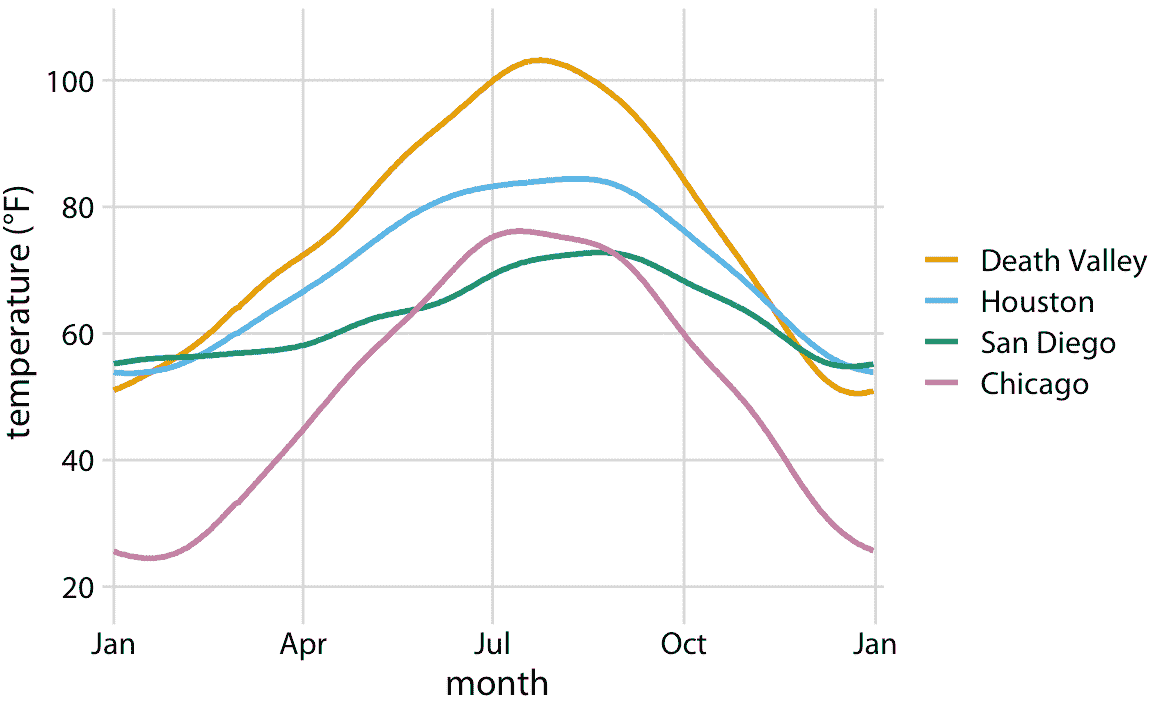  圖 2.3：美國四個選定位置的日平均氣溫，溫度映射到 *y* 軸，一年中的某一天映射到 *x* 軸，以及位置到線的顏色。數據來源：NOAA。 圖 2.3 是一個相當標準的溫度曲線可視化，可能是大多數數據科學家首先直觀選擇的可視化。但是，由我們決定哪些變量映射到哪個刻度。例如，不將溫度映射到 *y* 軸上，不將位置映射到顏色上，我們可以做相反的事情。因為現在感興趣的關鍵變量（溫度）顯示為顏色，我們需要顯示足夠大的顏色區域，以便顏色傳達有用信息（Stone，Albers Szafir 和 Setlur [2014](#ref-Stone_et_al_2014)）。因此，對于這種可視化，我選擇了正方形而不是線條，每個月和位置都有一個，我用每個月的平均氣溫對它們著色（圖 2.4）。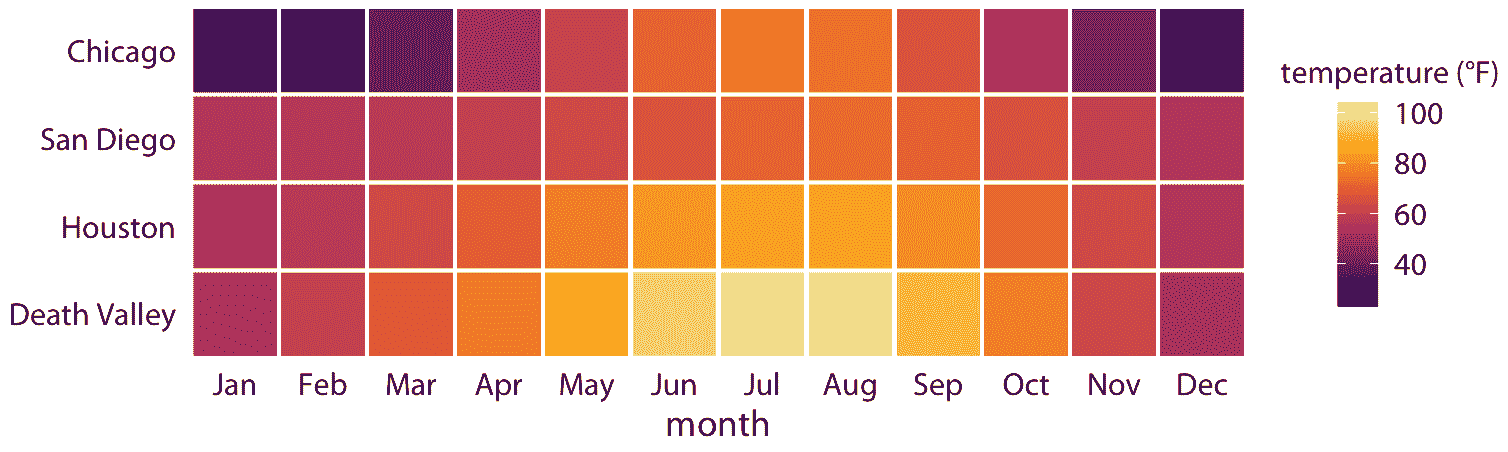  圖 2.4：美國四個地點的每月正常平均溫度數據來源：NOAA 我想強調的是，圖 2.4 使用兩個位置刻度（沿著 *x* 軸的月份和沿著 *y* 軸的站點），但兩者都不是連續刻度。月份是一個有 12 個水平的有序因子，位置是一個有四個水平的無序因子。因此，兩個位置刻度都是離散的。對于離散位置刻度，我們通常將因子的不同水平沿軸線以相等的間距放置。如果因子是有序的（就像這里的月份一樣），則需要按適當的順序放置水平。如果因子是無序的（這里是站點的情況），那么順序是任意的，我們可以選擇我們想要的任何順序。我排列了整體最冷（芝加哥）到整體最熱（死亡谷）的地點，來產生令人愉快的驚人色彩。但是，我可以選擇任何其他順序，這個圖形同樣有效。 圖 2.3 和 2.4 總共使用了三個刻度，兩個位置刻度和一個顏色刻度。這是基本可視化的典型刻度數，但我們可以同時使用三個以上的刻度。圖 2.5 使用五個刻度，兩個位置刻度，一個顏色，一個尺寸和一個形狀刻度，所有刻度表示來自數據集的不同變量。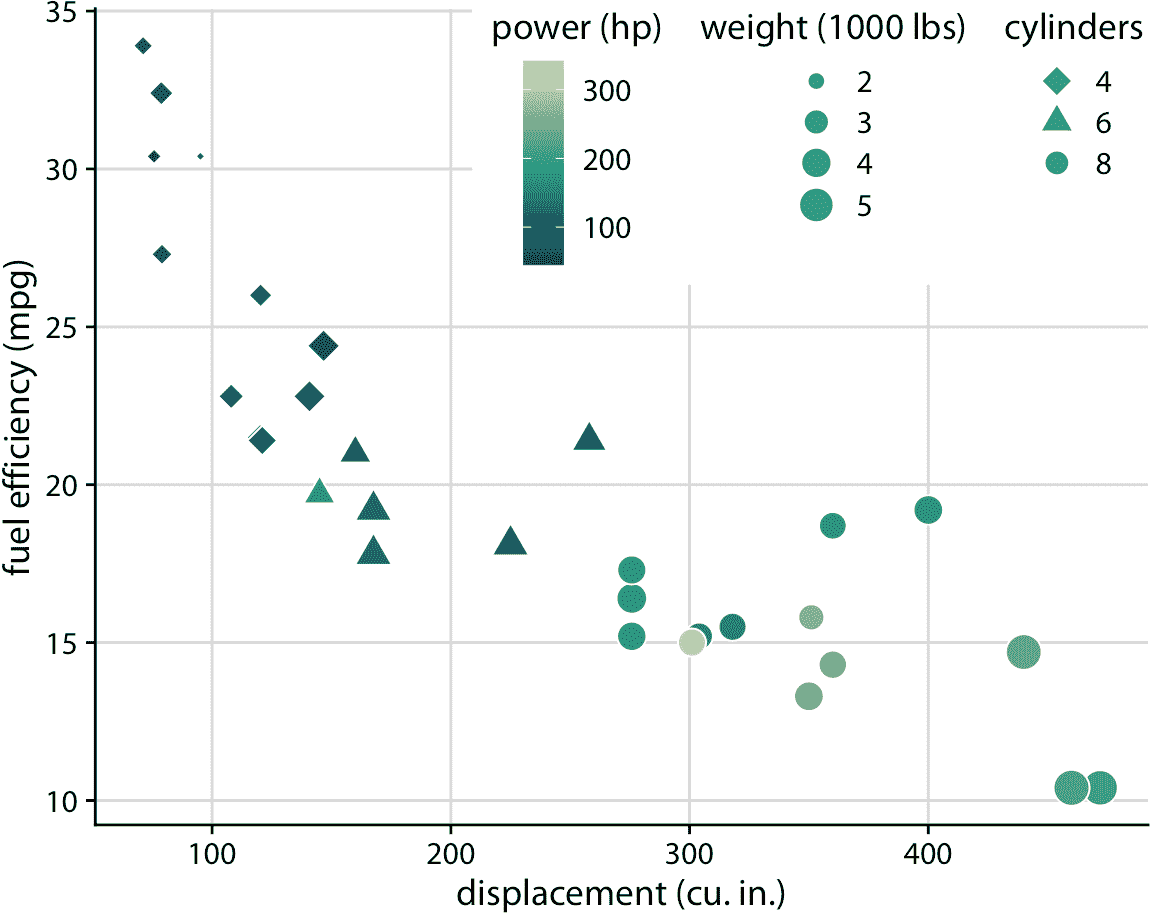  圖 2.5：32 輛汽車（型號為 1973-74）的燃油效率與排量。該圖使用五個單獨的刻度來表示數據： (i) *x* 軸（排量）； (ii) *y* 軸（燃油效率）； (iii) 數據點的顏色（功率）； (iv) 數據點的大小（重量）； (v) 數據點的形狀（缸數）。 顯示的五個變量中的四個（位移，燃料效率，功率和重量）是數值連續的。剩余的一個（缸數）可以被認為是數值離散的或定性的。數據來源：Motor Trend，1974。 ### 參考 ``` Stone, M., D. Albers Szafir, and V. Setlur. 2014. “An Engineering Model for Color Difference as a Function of Size.” In 22nd Color and Imaging Conference. Society for Imaging Science and Technology. ```