# 8 可視化分布：經驗累積分布函數和 q-q 圖 > 原文： [8 Visualizing distributions: Empirical cumulative distribution functions and q-q plots](https://serialmentor.com/dataviz/ecdf-qq.html) > 校驗：[飛龍](https://github.com/wizardforcel) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 在第七章中，我描述了如何使用直方圖或密度圖來可視化分布。這兩種方法都非常直觀且具有視覺吸引力。然而，正如該章中所討論的，它們有共同的限制，即所得圖形在很大程度上取決于用戶必須選擇的參數，例如直方圖的箱寬和密度圖的帶寬。因此，兩者都必須被視為對數據的解釋，而不是數據本身的直接可視化。 作為使用直方圖或密度圖的替代方法，我們可以簡單地將所有數據點單獨顯示為點云。但是，對于非常大的數據集，這種方法變得難以處理，并且在任何情況下，聚合方法中有一些值，突出顯示分布的屬性而不是單個數據點。為了解決這個問題，統計學家發明了經驗累積分布函數（ecdfs）和分位數-分位數（q-q）圖。這些類型的可視化不需要任意參數的選擇，它們一次顯示所有數據。不幸的是，它們比直方圖或密度圖更不直觀，我不認為它們在高科技出版物之外經常使用。不過，他們在統計學家中很受歡迎，我認為任何對數據可視化感興趣的人都應該熟悉這些技術。 ## 8.1 經驗累積分布函數 為了說明累積的經驗分布函數，我將從一個假設的例子開始，該例子使用我在教室里作為教授大量處理的東西來建模：學生成績的數據集。假設我們的班有 50 名學生，學生們剛剛完成了考試，他們的得分在 0 到 100 分之間。我們如何才能最好地可視化課堂表現，例如來確定適當的成績界限？ 我們可以繪制得分不超過某個值的學生總數與所有可能的得分。該圖將是一個升序函數，從 0 分和 0 人開始，到 100 分和 50 人結束。關于這種可視化的另一種思考方式如下：我們可以按所獲得的分數按升序對所有學生進行排名（使得分最低的學生排名最低，得分最高的學生排名最高） ，然后繪制排名與獲得的實際得分。結果是經驗累積分布函數（ecdf）或簡單稱為累積分布。每個點代表一個學生，并且線條展示了對于任何的可能得分，觀察到的學生的最高排名（圖 8.1）。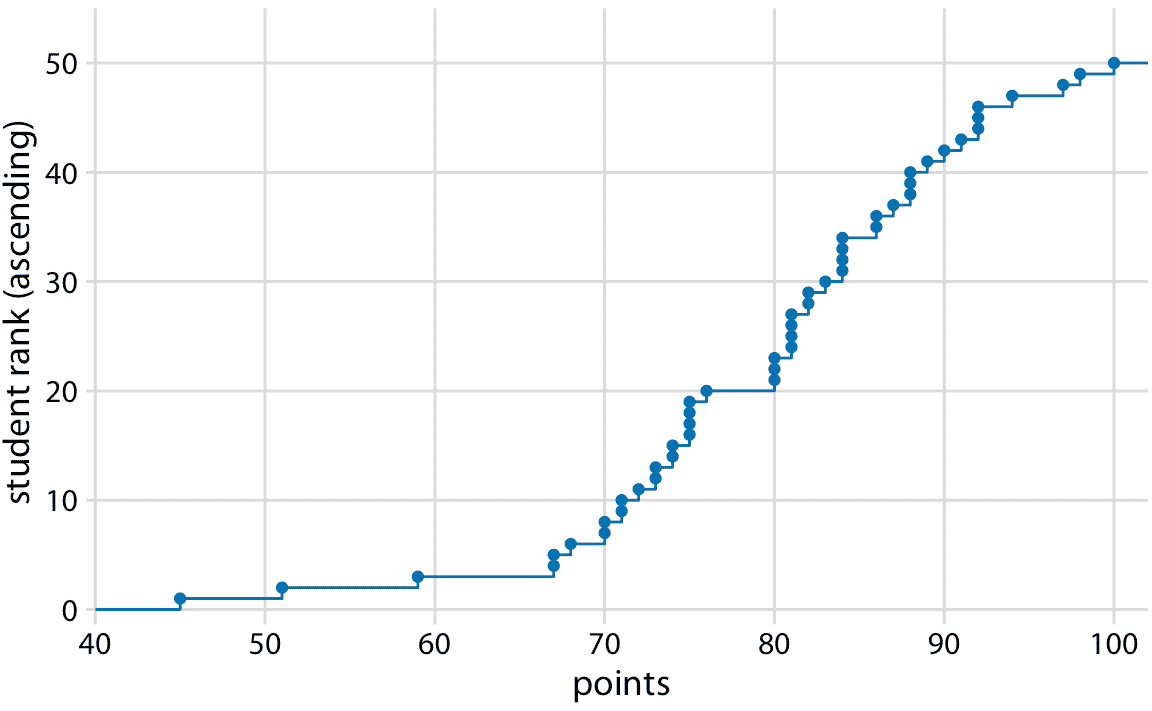  圖 8.1：假設的 50 名學生的學生成績的經驗累積分布函數。 你可能想知道如果我們按照相反的順序對學生進行排序，會發生什么。這個排名簡單地翻轉了它的函數。結果仍然是經驗累積分布函數，但現在這些線表示對于任何可能的得分，觀察到的最低學生排名（圖 8.2）。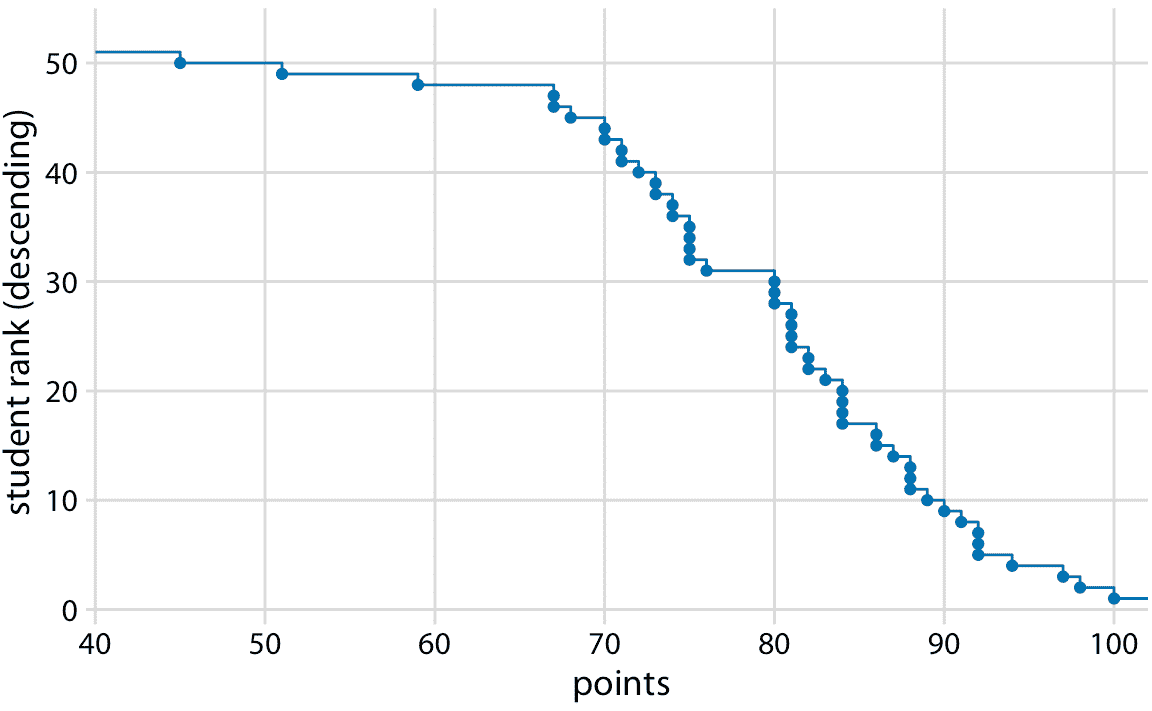  圖 8.2：作為降序 ecdf 繪制的學生成績分布。 升序累積分布函數比降序函數更廣為人知，更常用，但兩者都有重要的應用。當我們想要顯示高度偏斜的分布時，降序累積分布函數是至關重要的（參見章節 8.2 ）。 在實際應用中，繪制 ecdf 而不突出顯示各個點，并通過最大排名對排名進行歸一化是很常見的，因此 *y* 軸代表累積頻率（圖 8.3）。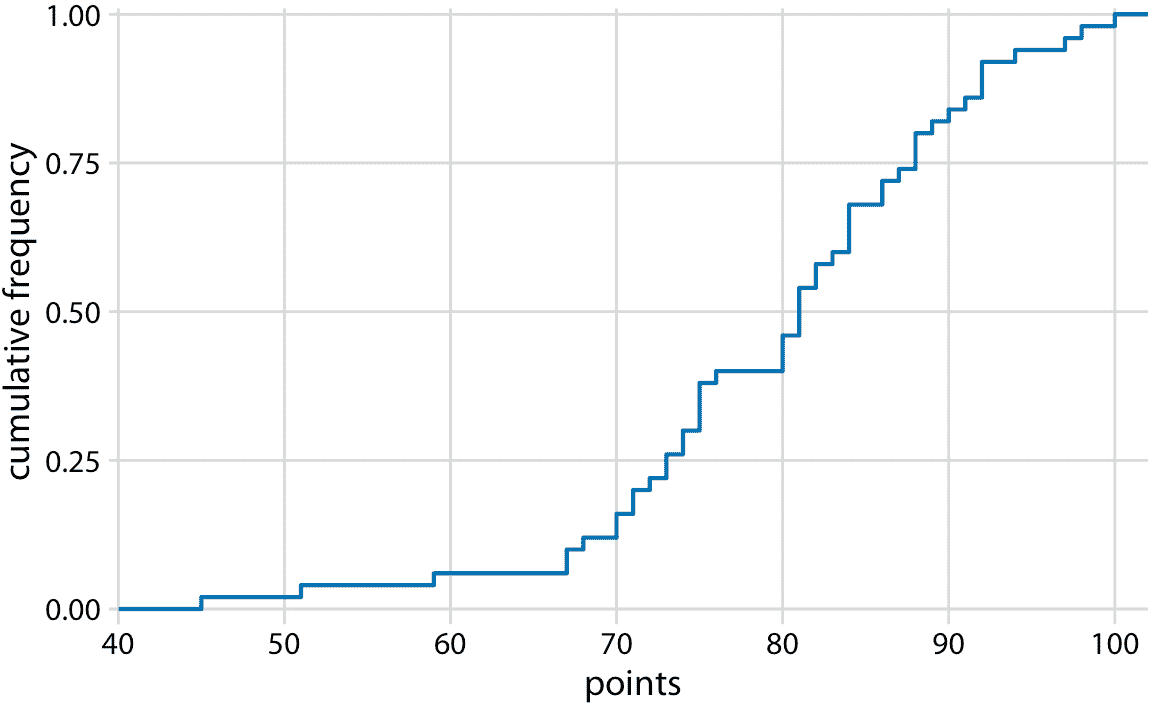  圖 8.3：學生成績的 Ecdf。學生排名已經按照學生總數標準化，因此繪制的 *y* 值對應于班級中得分不超過一定值的學生的比例。 我們可以直接從該圖中讀取學生成績分布的關鍵屬性。例如，大約四分之一的學生（25%）得到不到 75 分。中點值（對應于 0.5 的累積頻率）是 81。大約 20% 的學生得到 90 分或更多。 我發現 ecdfs 可以方便地分配成績邊界，因為它們可以幫助我找到最小化學生不快樂的準確截斷點。例如，在這個例子中，在 80 分以下有一條相當長的水平線，接著是 80 分的急劇上升。這個特征的成因是三名學生在考試中獲得 80 分，而另一名表現較差的學生只獲得 76 分。在這種情況下，我可能會認為得分為 80 或者以上的每個人都會得到一個 B，而且每個 79 或者更少的人都會得到 C。這三個 80 分的學生很高興他們剛得到了一個 B，而那個 76 分的學生意識到他必須表現得更好才能不得到 C。如果我把截斷值設定為 77，那么字母等級的分布就完全一樣了，但我可能會發現，76 分的學生來我辦公室，希望協商他們的成績。同樣，如果我將截斷值設置為 81，在我的辦公室里可能會有三名學生試圖協商他們的成績。 ## 8.2 高度偏斜的分布 許多經驗數據集具有高度偏斜的分布，特別是右邊的重尾，這些分布可能具有挑戰性。此類分布的示例包括居住在不同城市或縣的人數，社交網絡中的聯系人數，單個單詞出現在書中的頻率，不同作者撰寫的學術論文數量，個體凈值，以及蛋白質相互作用網絡中單個蛋白質的相互作用伙伴的數量（Clauset，Shalizi 和 Newman，2009）。所有這些分布的共同點是它們的右尾衰減比指數函數慢。實際上，這意味著非常大的值并不罕見，即使分布的平均值很小。一類重要的此類分布是冪律分布，其中觀測值 *x* 大于某些參考點的值的可能性降為 *x* 的冪。舉一個具體的例子，考慮美國的凈值，它是冪為 2 的指數分布。在任何給定的凈值水平（比如 100 萬美元），凈值為一半的人是四倍，凈值為兩倍的人是四分之一。重要的是，如果我們使用 10,000 美元作為參考點或者我們使用 1 億美元，那么同樣的關系也成立。因此，冪律分布也稱為無刻度分布。 根據 2010 年美國人口普查，我將首先討論生活在美國各州的人數。這種分布在右邊有一個很長的尾巴。盡管大多數縣的居民人數相對較少（中位數為 25,857），但仍有少數縣擁有極大數量的居民（例如洛杉磯縣，居民人數為 9,818,605）。如果我們試圖將人口分布可視化為密度圖或 ecdf，我們獲得的數據基本上是無用的（圖 8.4）。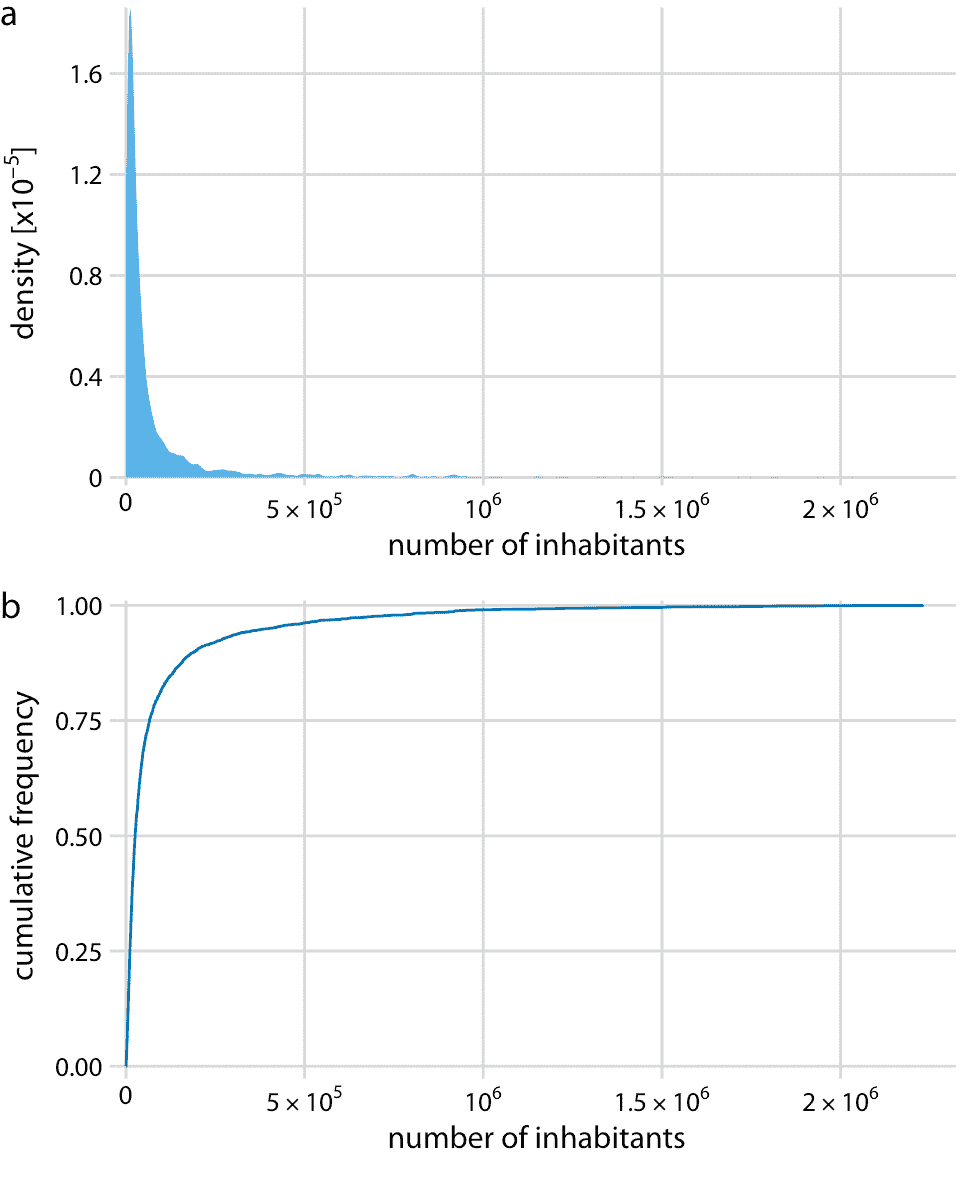  圖 8.4：根據 2010 年美國人口普查，美國各縣的居民人數分布。（a）密度圖。 （b）經驗累積分布函數。 密度圖（圖 8.4a）在 0 處有一個尖峰，幾乎沒有可見的分布細節。類似地，ecdf（圖 8.4b）在 0 附近快速上升，并且同樣沒有可見的分布細節。對于此特定數據集，我們可以對數據進行對數轉換并可視化對數轉換值的分布。這種轉換在這里起作用，因為縣里的人口數量實際上并不是冪律，而是遵循近乎完美的對數正態分布（參見 8.3 部分）。實際上，對數變換值的密度圖顯示出良好的鐘形曲線，相應的 ecdf 顯示出良好的 S 形形狀（圖 8.5）。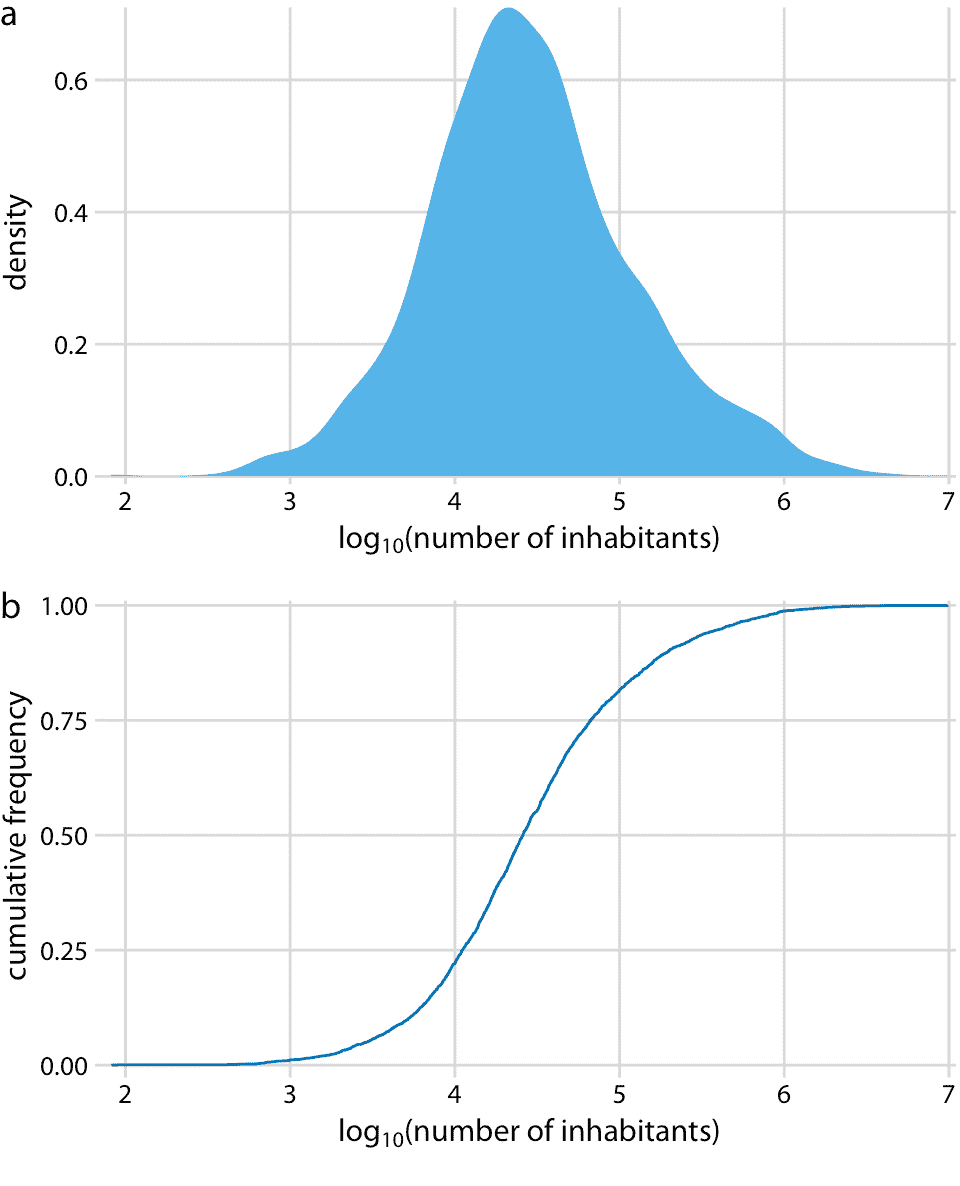  圖 8.5：美國各縣居民人數的對數分布。（a）密度圖。（b）經驗累積分布函數。 為了查看這個分布不是冪律，我們將其繪制為具有對數 *x* 和 *y* 軸的降序 ecdf。在此可視化中，冪律顯示為完美的直線。對于縣里的人口數量，右尾在降序雙對數 ecdf 圖上幾乎是一條直線，但不是很像（圖 8.6）。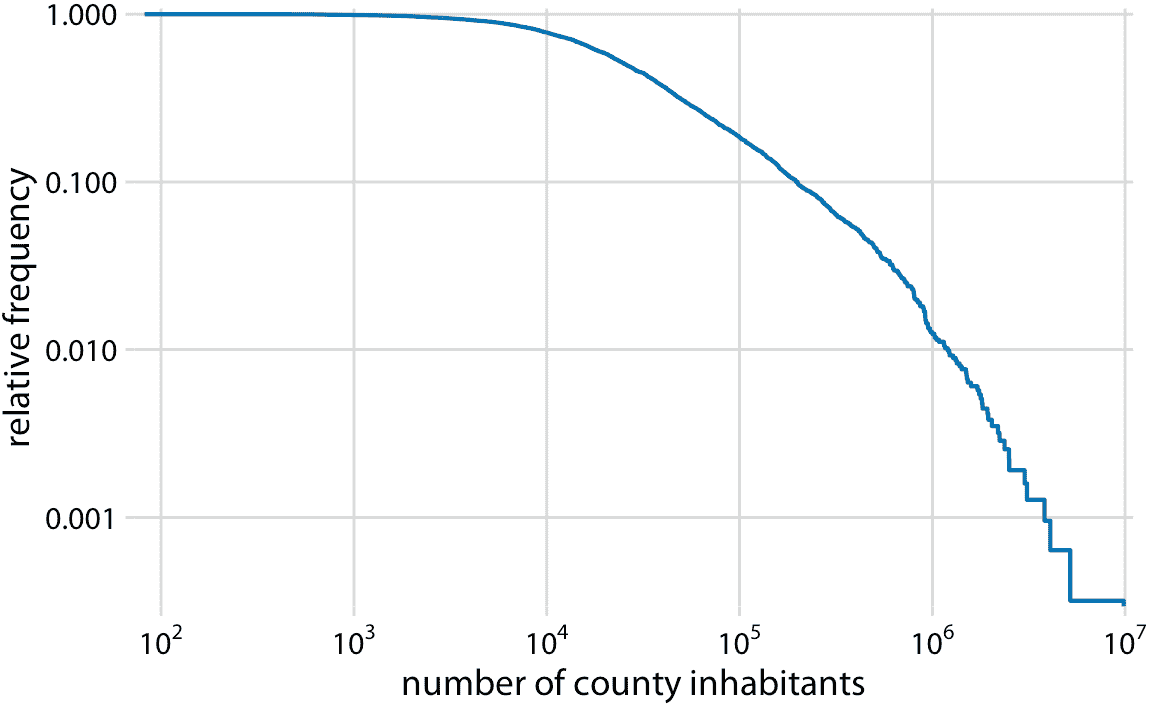  圖 8.6：至少有一定居民的縣的相對頻率，與縣居民的數量。 作為第二個例子，我將使用出現在小說“白鯨記”中的所有單詞的詞頻分布。這種分布遵循完美的冪律。當使用對數軸繪制為降序 ecdf 時，我們看到幾乎完美的直線（圖 8.7 ）。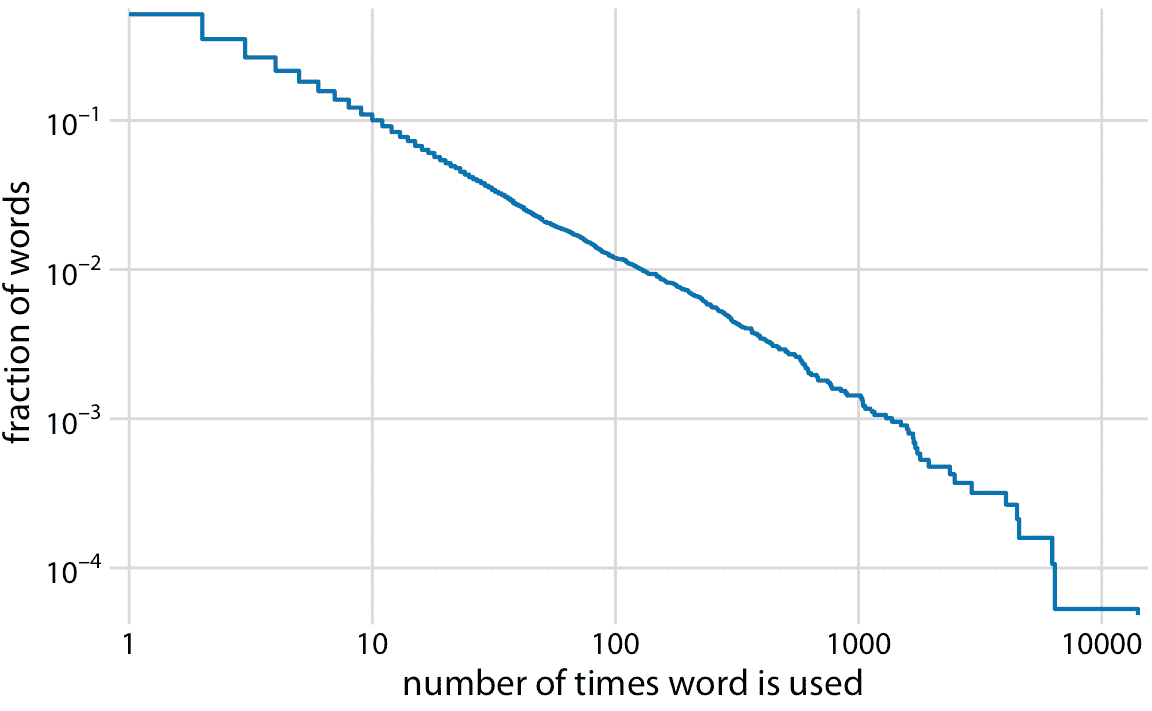  圖 8.7：小說“白鯨記”中詞數的分布。顯示的是在小說中至少出現一定次數的單詞的相對頻率與使用單詞的次數。 ## 8.3 分位數-分位數圖 當我們想要確定觀察到的數據點在何種程度上遵循給定分布時，分位數-分位數（q-q）圖是有用的可視化。就像 ecdfs 一樣，q-q 圖也基于對數據進行排名，并可視化排名和實際值之間的關系。但是，在 q-q 圖中，我們不直接繪制排名，如果數據是根據指定的參考分布而分布的，我們使用它們來預測給定數據點應該落在哪里。最常見的是，使用正態分布作為參考構建 q-q 圖。舉一個具體的例子，假設實際數據值的平均值為 10，標準差為 3。然后，假設正態分布，我們預計排在百分位數 50 的數據點值為 10（平均值） ，百分位 84 的數據點值為 13（高于平均值一個標準差），百分位 2.3 的數據點值為 4（平均值以下兩個標準差）。我們可以對數據集中的所有點執行該計算，然后繪制觀測值（即，數據集中的值）與理論值（即，給定每個數據點的排名和假定的參考分布的預期值）。 當我們從本章開頭對學生成績分布執行此過程時，我們得到圖 8.8 。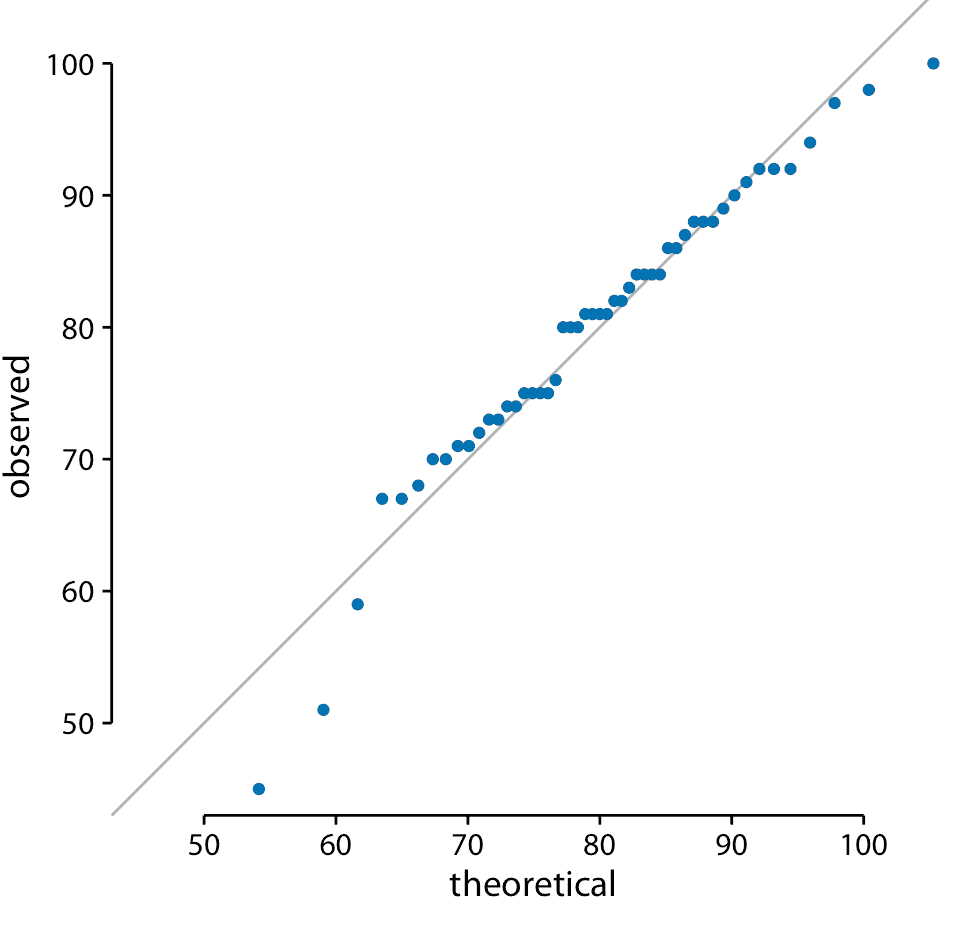  圖 8.8：學生成績的 q-q 圖。 這里的實線不是回歸線，而是表示 *x* 等于 *y* 的點，即觀察值等于理論值的點。如果點落在該線上，則數據遵循假設分布（此處為正態）。我們發現學生的成績主要是正態分布，在底部和頂部有一些偏差（少數學生的表現比預期更差）。分布的頂部偏差是由假設檢驗中的最大點值 100 引起的；無論最好的學生有多好，他或她最多可以獲得 100 分。 我們還可以使用 q-q 圖來測試我在本章前面的斷言，即美國各縣的人口數量遵循對數正態分布。如果這些計數是對數正態分布的，那么它們的對數變換值是正態分布的，因此應該直接落在 *x* = *y* 線上。在制作這個圖時，我們看到觀測值與理論值之間的一致性是異常的（圖 8.9）。這表明縣之間人口數量的分布確實是對數正態的。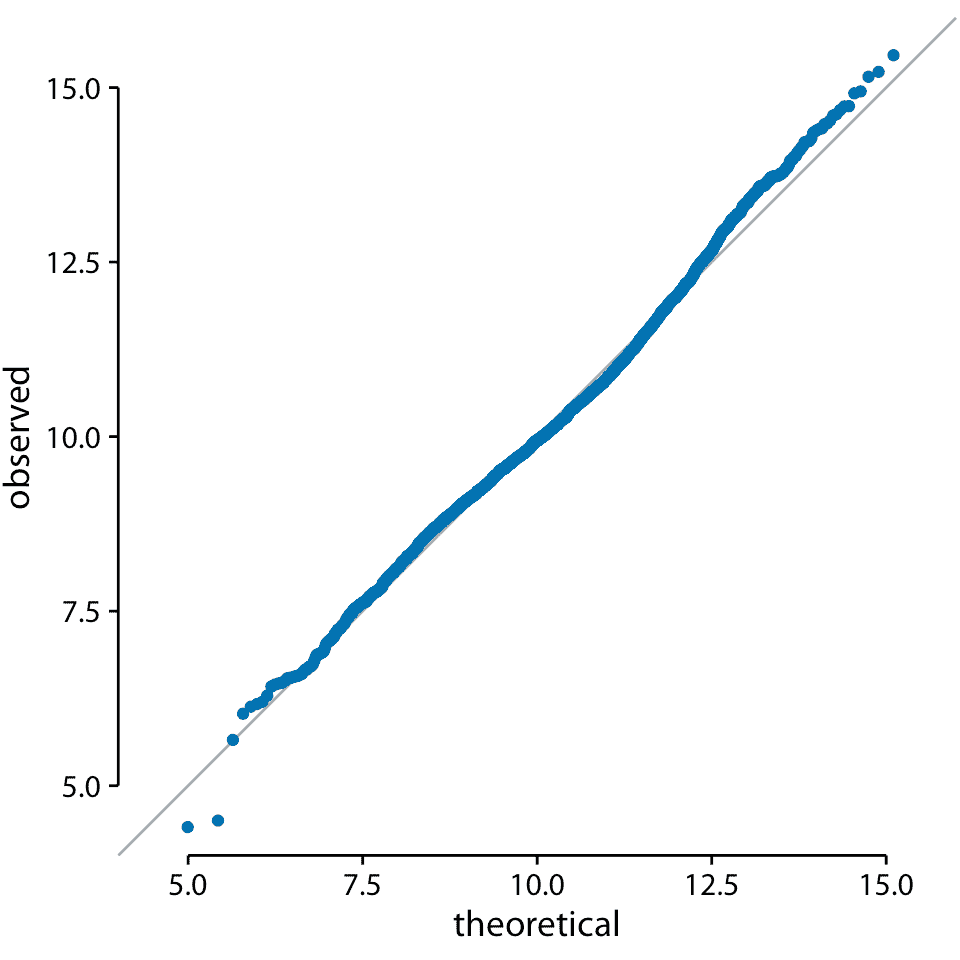  圖 8.9：美國各縣居民人數對數的 q-q 圖。 ### 參考 ``` Clauset, A., C. R. Shalizi, and M. E. J. Newman. 2009. “Power-Law Distributions in Empirical Data.” SIAM Review 51: 661–703. ```