# 3 坐標系和軸 > 原文： [3 Coordinate systems and axes](https://serialmentor.com/dataviz/coordinate-systems-axes.html) > 校驗：[飛龍](https://github.com/wizardforcel) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 要進行任何類型的數據可視化，我們需要定義位置刻度，來確定不同數據值的在圖形中的位置。如果不將不同數據點放置在不同位置，我們就無法可視化數據，即使我們只是沿著一條線將它們彼此相鄰排列。對于常規的 2d 可視化，需要兩個數字來唯一地指定一個點，因此我們需要兩個位置刻度。這兩個刻度通常但不一定是圖的 *x* 和 *y* 軸。我們還必須指定這些刻度的相對幾何排列。通常， *x* 軸水平延伸，*y* 軸垂直，但我們可以選擇其他排列。例如，我們可以使 *y* 軸相對于 *x* 軸成銳角，或者我們可以讓一個軸成圓形而另一個軸徑向延伸。一組位置刻度及其相對幾何排列的組合稱為坐標系。 ## 3.1 笛卡爾坐標 最廣泛使用的數據可視化坐標系是 2d 笛卡爾坐標系，其中每個位置由 *x* 和 *y* 值唯一指定。 *x* 和 *y* 軸彼此正交，數據值沿兩個軸均等間隔放置（圖 3.1 ）。兩個軸是連續的位置刻度，它們可以表示正實數和負實數。要完全指定坐標系，我們需要指定每個軸覆蓋的數字范圍。在圖 3.1 中， *x* 軸從 -2.2 到 3.2，*y* 軸從 -2.2 到 2.2。這些軸邊界之間的任何數據值都放置在圖中的相應位置。軸邊界之外的任何數據值都將被丟棄。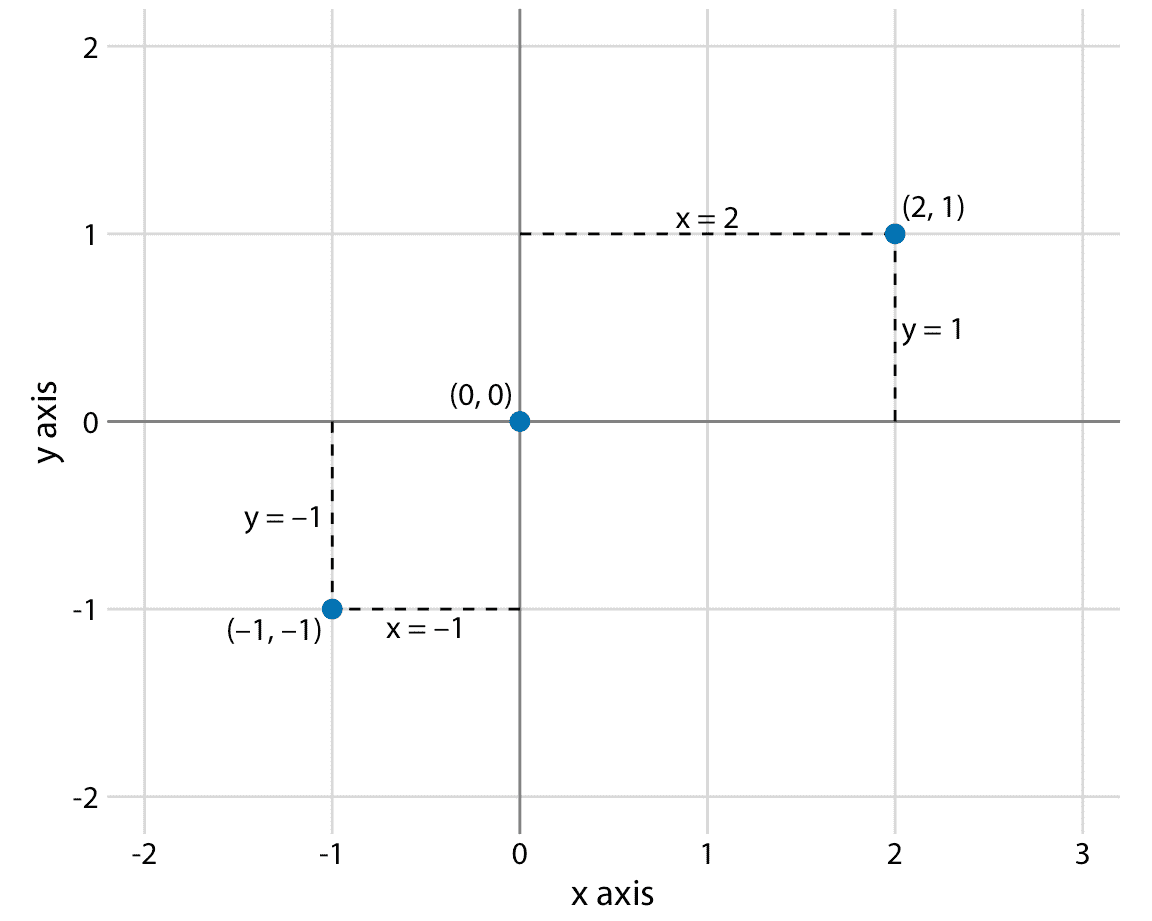  圖 3.1：標準笛卡爾坐標系。橫軸通常稱為 *x*，縱軸為 *y* 。兩個軸形成等間距的網格。這里， *x* 和 *y* 網格均以 1 為單位分開。點`(2, 1)`位于原點`(0, 0)`右側的兩個 *x* 單位和上方的一個 *y* 單位。點`(-1, -1)`位于原點左側的一個 *x* 單位和位于下方的一個 *y* 單位。 但是，數據的值通常不僅僅是數字。他們有單位。例如，如果我們測量溫度，則可以以攝氏度或華氏度為單位。類似地，如果我們測量距離，則可以以公里或英里為單位，如果我們測量持續時間，則可以以分鐘，小時或天為單位。在笛卡爾坐標系中，沿軸的網格線之間的間距對應于這些數據單元中的離散步長。例如，在溫度范圍內，我們可能每 10 華氏度有一個網格線，而在距離范圍內，我們可能每 5 公里有一個網格線。 笛卡爾坐標系可以具有代表兩個不同單位的兩個軸。每當我們將兩種不同類型的變量映射到 *x* 和 *y* 時，就會出現這種情況。例如，在圖 2.3 中，我們繪制了溫度與一年中的天數。圖 2.3 的 *y* 軸以華氏度為單位測量，網格線均為 20 度，*x* 軸以月為單位測量，網格線在每三個月的第一個月。無論何時以不同的單位測量兩個軸，我們都可以相對于另一個軸拉伸或壓縮，并保持數據的有效可視化（圖 3.2 ）。哪個版本更合適，取決于我們想傳達的故事。高而窄的圖形強調沿 *y* 軸的變化，而短而寬的圖形則相反。理想情況下，我們希望選擇一個寬高比，以確保任何位置上的重要差異都是顯而易見的。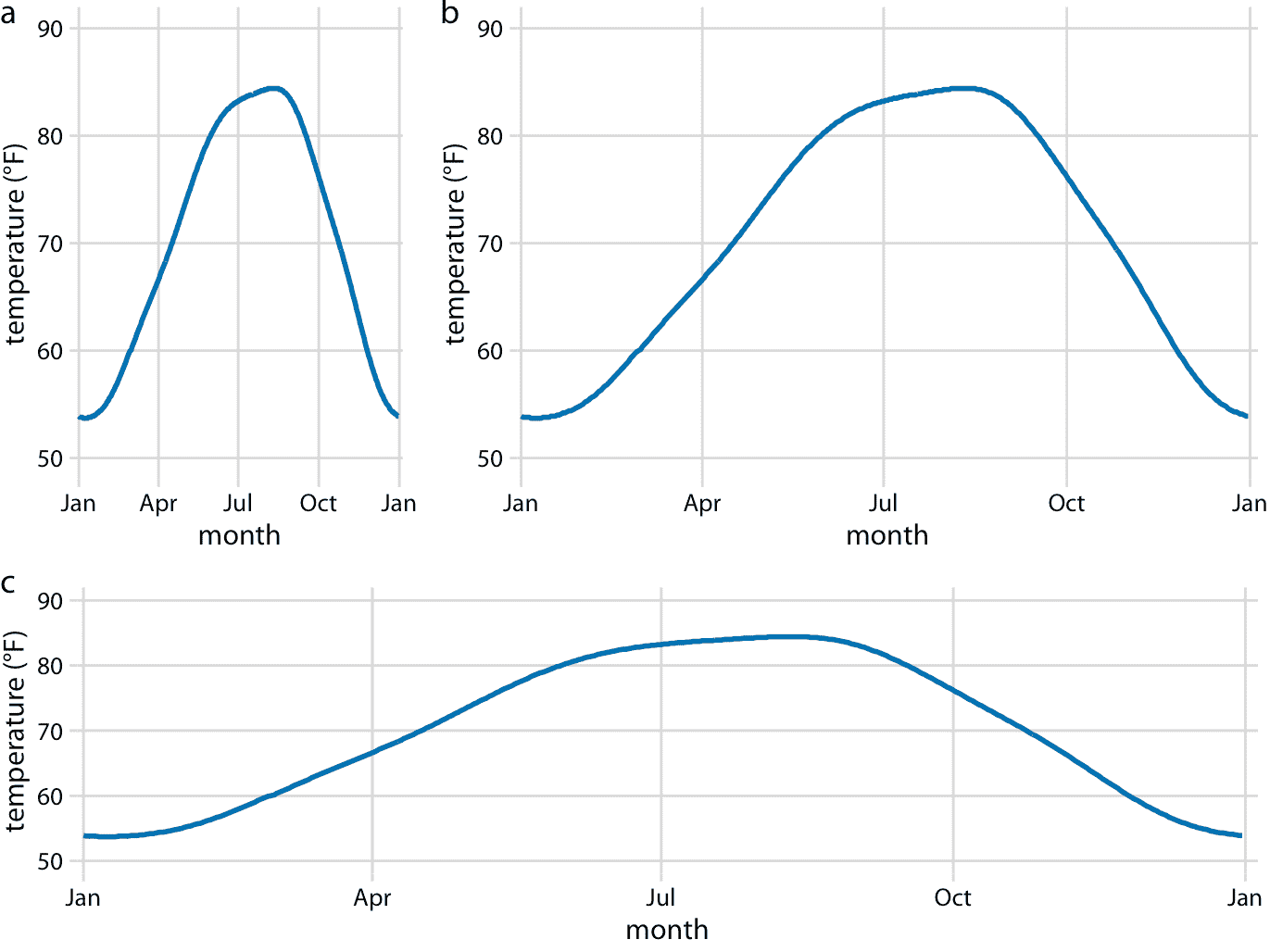  圖 3.2：德克薩斯州休斯頓的日平均溫度。溫度映射到 *y* 軸以及一年中的某一天映射到 *x* 軸。部分（a），（b）和（c）以不同的縱橫比展示相同的圖。所有三個部分都是溫度數據的有效可視化。數據來源：NOAA。 另一方面，如果 *x* 和 *y* 軸以相同的單位測量，那么兩個軸的網格間距應該相等，這樣沿著 *x* 或 *y* 軸的相同的距離，對應于相同數量的數據單位。例如，我們可以繪制一年中每天的休斯頓，德克薩斯州與加利福尼亞州圣地亞哥的溫度（圖 3.3a）。由于沿兩個軸繪制相同的定量值，我們需要確保網格線形成完美的正方形，如圖 3.3 中的情況。  圖 3.3：休斯頓，TX 的日平均溫度，相對于加利福尼亞州圣地亞哥的相應平均溫度繪制。突出顯示 1 月，4 月，7 月和 10 月的第一天，來提供時間參考。 （a）氣溫以華氏度表示。 （b）溫度以攝氏度表示。數據來源：NOAA。 您可能想知道如果更改數據單位會發生什么。畢竟，單位是任意的，你的偏好可能與其他人不同。單位變化是線性變換，我們在所有數據值中添加或減去一個數字和/或將所有數據值與另一個數字相乘。幸運的是，笛卡爾坐標系在這種線性變換下是不變的。因此，您可以更改數據的單位，只要相應地更改軸，所得圖形就不會改變。例如，比較圖 3.3a 和 3.3b。兩者都顯示相同的數據，但在部分（a）中溫度單位是??華氏度，而在部分（b）中它們是攝氏度。即使網格線位于不同的位置并且沿軸的數字不同，兩個數據可視化看起來完全相同。 ## 3.2 非線性軸 在笛卡爾坐標系中，沿軸的網格線在數據單元和所得可視化中均勻間隔。我們將這些坐標系中的位置刻度稱為線性的。雖然線性刻度通常提供數據的準確表示，但是存在非線性刻度更佳的情況。在非線性刻度中，數據單元中的均勻間距對應于可視化中的不均勻間隔，或者相反地，甚至可視化中的間距對應于數據單元中的不均勻間隔。 最常用的非線性刻度是對數（log）刻度。對數刻度在乘法中是線性的，因此刻度上的單位步長相當于乘上固定值。要創建對數刻度，我們需要對數據值進行對數轉換，同時對沿軸網格線顯示的數字進行求冪。該過程在圖 3.4 中進行了演示，其中顯示了在線性和對數刻度上的數字 1, 3.16, 10, 31.6 和 100。數字 3.16 和 31.6 似乎是一個奇怪的選擇，但選擇它們是因為它們正好在 1 到 10 之間，在對數刻度上在 10 到 100 之間。我們可以通過觀察 $10 ^ {0.5} = \sqrt{10} \sim 3.16$ 和等價的 $3.16 \times 3.16 \sim 10 $ 來看到這一點。類似地，$10^{1.5} = 10 \times 10^{0.5} \sim 31.6$。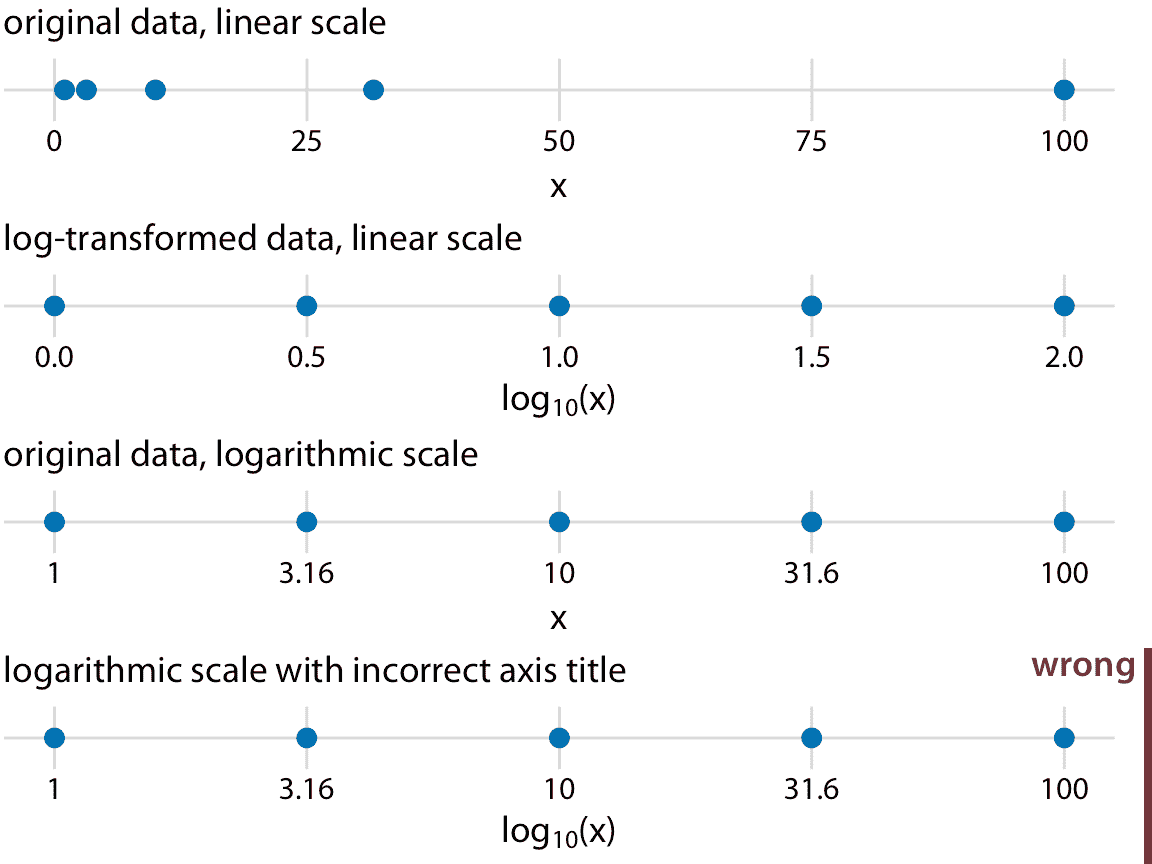  圖 3.4：線性和對數刻度之間的關系。點對應于數據值 1, 3.16, 10, 31.6, 100，它們是對數刻度上的均勻間隔數。我們可以在線性刻度上顯示這些數據點，我們可以對它們進行對數轉換然后以線性刻度顯示，或者我們可以在對數刻度上顯示它們。重要的是，對數刻度的正確軸標題是顯示的變量的名稱，而不是該變量的對數。 在數學上，在線性刻度上繪制對數變換數據，或在對數刻度上繪制原始數據之間沒有區別（圖 3.4 ）。唯一的區別在于單個軸刻度線和整個軸的標簽。在大多數情況下，對數刻度的標簽是優選的，因為它對讀者施加較少的精神負擔，來解釋顯示為軸刻度線標簽的數字。關于對數基數的混淆風險也較小。當使用對數轉換的數據時，我們可能會對數據是使用自然對數還是使用基數 10 的對數感到困惑。不常見的標簽是模棱兩可的，例如： `log(x)`，它根本沒有指定基數。我建議您在使用對數轉換數據時始終標明基數。繪制對數轉換的數據時，請始終在軸標簽中指定基數。 因為對數刻度上的乘法看起來像線性刻度上的加法，所以對數刻度是通過乘法或除法獲得的任何數據的自然選擇。特別是，比值通常應以對數刻度顯示。例如，我已經記錄了德克薩斯州每個縣的居民人數，并將其除以德克薩斯州所有縣的居民人數中位數。得到的比值是可以大于或小于 1 的數字。恰好為 1 的比值意味著相應的縣具有居民的中位數。當以對數刻度可視化這些比值時，我們可以清楚地看到，德克薩斯州的人口數量對稱地分布在中位數附近，并且人口最多的縣的人數比中位數多 100 多倍，而人口最少的縣則少 100 多倍（圖 3.5 ）。相比之下，對于相同的數據，線性刻度模糊了中等人口數量的縣與人口數量小于中位數的縣之間的差異（圖 3.6）。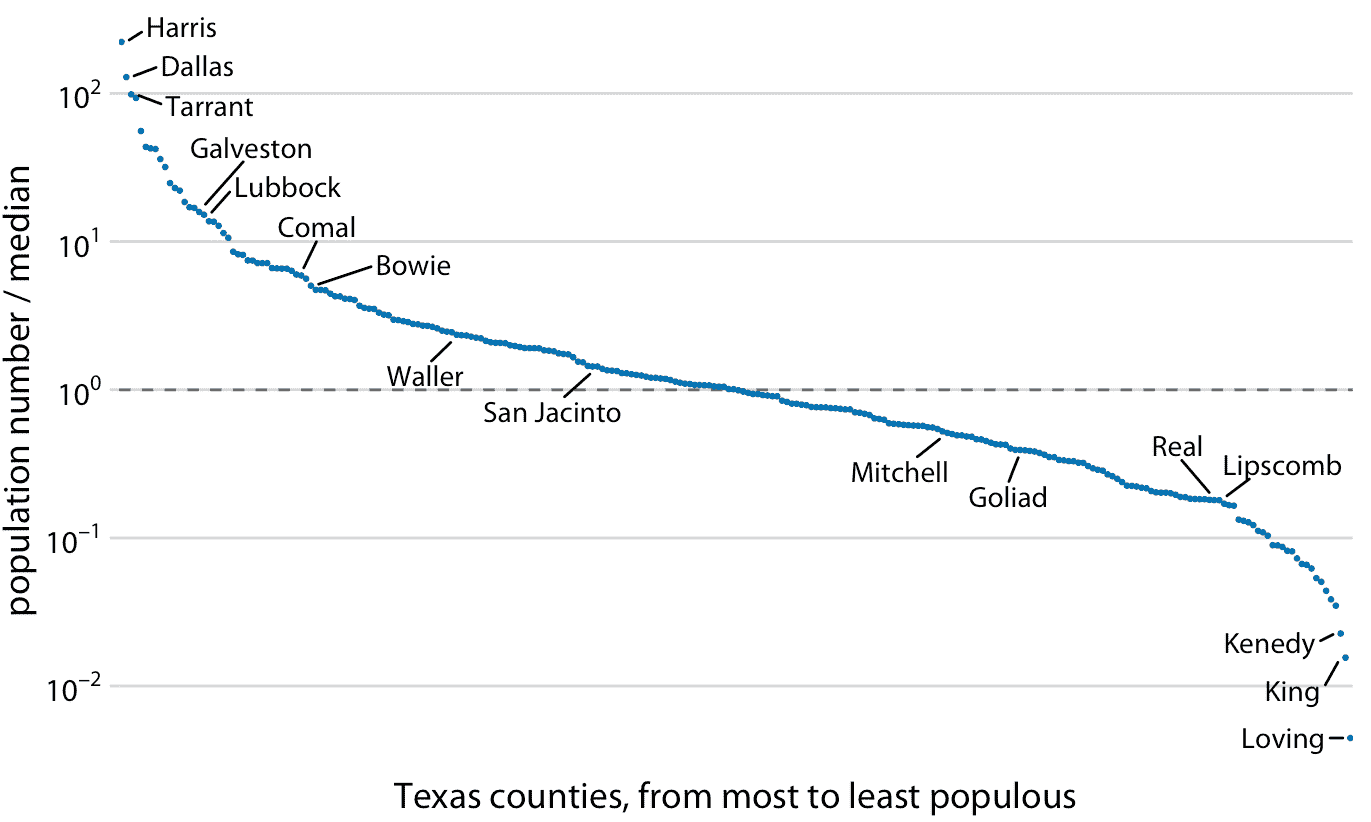  圖 3.5：德克薩斯州的人口數量與其中值的關系。選擇縣按名稱突出顯示。虛線表示比值為 1，對應于具有中值人口數的縣。人口最多的縣的居民人數比中位數縣大約多 100 倍，人口最少的縣居民人數比中位數縣少 100 倍。數據來源：2010 年美國十年普查。  圖 3.6：德克薩斯州的人口規模與其中值的關系。通過在線性刻度上顯示比值，我們過分強調了大于 1 的比值，并且模糊了小于 1 的比值。作為一般規則，比值不應以線性刻度顯示。數據來源：2010 年美國十年普查。 在對數刻度上，值 1 是自然中點，類似于線性刻度上的值 0。我們可以認為大于 1 的值表示乘法而小于 1 的值表示除法。例如，我們可以寫`10 = 1 x 10`和`0.1 = 1 / 10`。另一方面，值 0 永遠不會出現在對數刻度上。它遠離 1。它的一個方法是考慮`log0 = -inf`。或者，考慮從 1 到 0，它需要除以無限多個有限值（例如，`1/10/10/10/10/10/10 ... = 0`或者一個除以無窮大（即`1 / inf = 0`）。 當數據集包含規模非常不同的數量時，經常使用對數刻度。對于圖 3.5 和 3.6 中顯示的德克薩斯州，人口最多的縣（Harris）在 2010 年美國人口普查中有 4,092,459 名居民，而人口最少的縣（Loving）有 82 人。所以即使我們沒有將人口數量除以中位數來將他們變成比值，對數刻度也是合適的。但如果有一個擁有 0 居民的縣，我們會怎么做？這個縣無法以對數刻度顯示，因為它位于負無窮大。在這種情況下，建議有時使用平方根刻度，它使用平方根變換而不是對數變換（圖 3.7 ）。就像對數刻度一樣，平方根刻度將較大的數字壓縮成較小的范圍，但與對數刻度不同，它允許存在 0。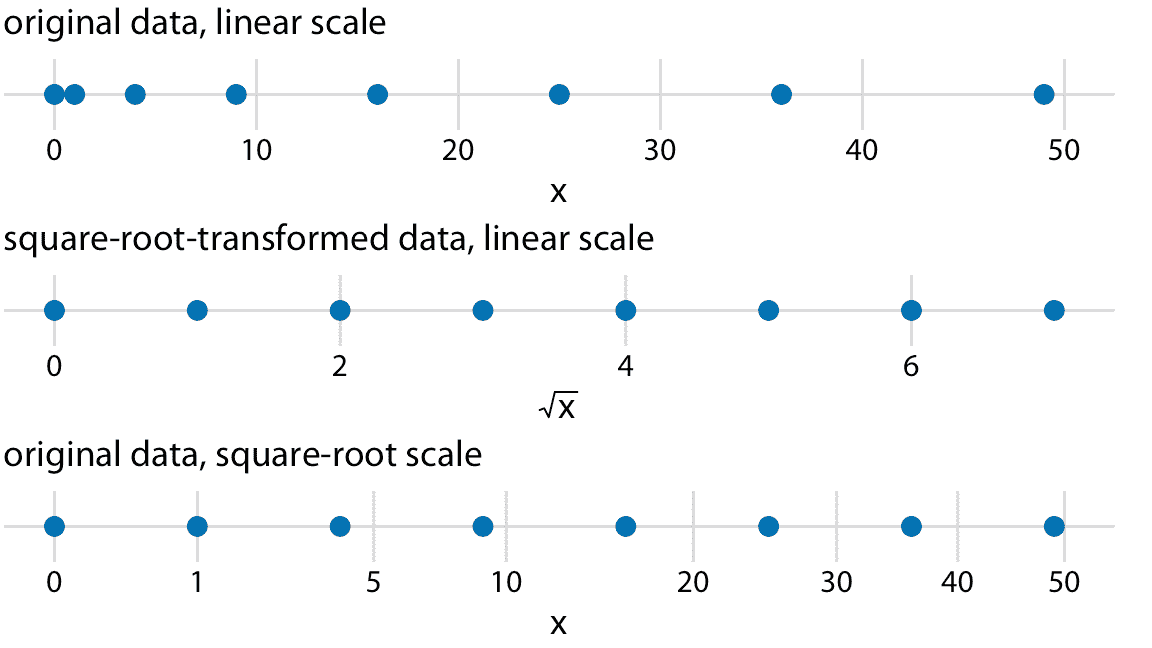  圖 3.7：線性和平方根刻度之間的關系。點對應于數據值 0, 1, 4, 9, 16, 25, 36, 49，它們是平方根刻度上的等間隔數，因為它們是從 0 到 7 的整數的平方。我們可以以線性刻度顯示這些數據點，我們可以對它們進行平方根變換然后以線性刻度顯示，或者我們可以在平方根刻度上顯示它們。 我看到了平方根刻度的兩個問題。首先，雖然在線性刻度上，一個單位步長對應于常數值的加或減，并且在對數刻度上它對應于常數值的乘或除，平方根刻度不存在這樣的規則。平方根刻度上的單位步長的含義取決于我們開始時的刻度值。其次，目前還不清楚如何最好地將軸刻度線放在平方根刻度上。為了獲得等間隔的刻度，我們必須將它們放置在正方形上，但是在例如位置 0, 4, 25, 49, 81（每個偶數的平方）處的軸刻度線將非常不直觀。或者，我們可以以線性間隔（10, 20, 30 等）放置它們，但這會導致刻度的小端附近的軸刻度線太少，或在大端附近太多。在圖 3.7 中，我將軸刻度線放在平方根刻度上的位置 0, 1, 5, 10, 20, 30, 40 和 50 處。這些值是任意的，但可以合理覆蓋數據范圍。 盡管平方根刻度存在這些問題，但它們是有效的位置刻度，我并不打算否認它們具有適當應用的可能性。例如，就像對數刻度是比值的自然刻度一樣，人們可以爭辯說，平方根刻度是平方數據的自然刻度。數據是自然平方的一種情況是在地理面積的背景下。如果我們以平方根刻度顯示地理面積，我們將突出顯示區域從東到西或從北到南的線性范圍。例如，如果我們想知道開車穿過一個地區可能需要多長時間，這些范圍可能是相關的。圖 3.8 以線性和平方根刻度顯示美國東北部的州的面積。即使這些州的面積完全不同（圖 3.8 a），穿過每個州所需的時間將更接近于平方根刻度上的數字（圖 3.8b）而不是線性刻度上的數字（圖 3.8a）。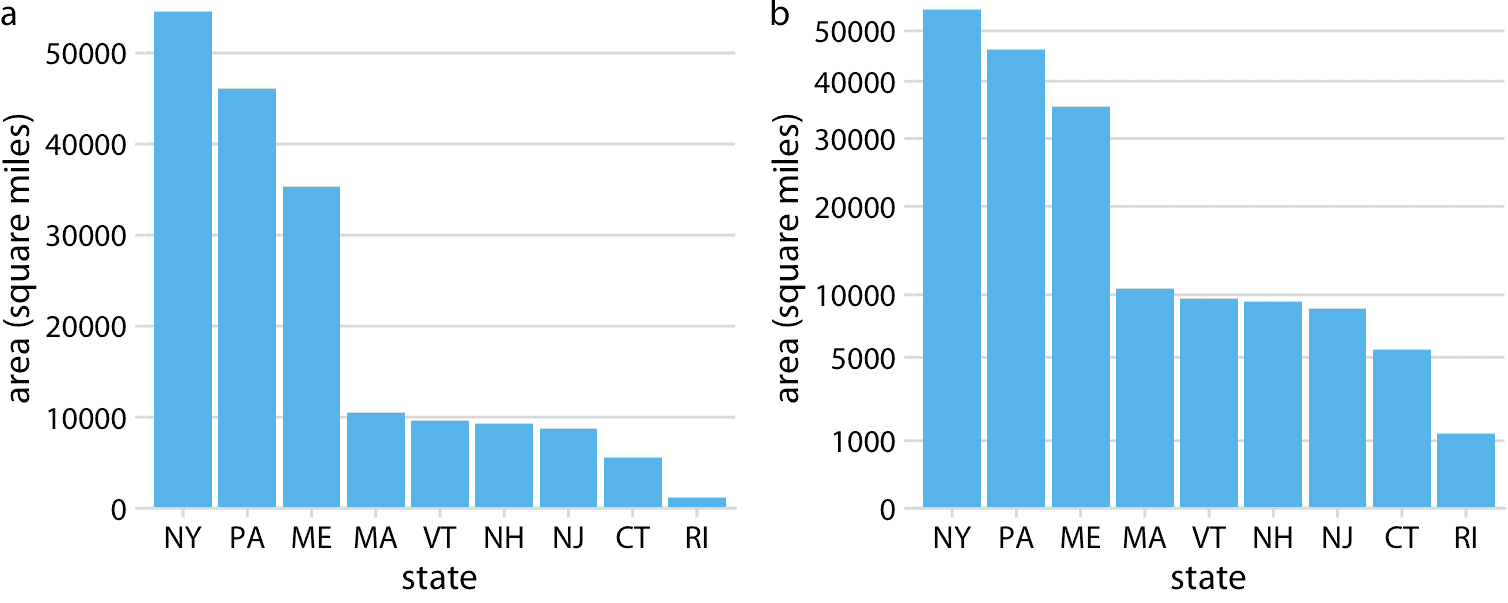  圖 3.8：美國東北部各州的面積。（a）以線性刻度顯示的面積。 （b）以平方根刻度顯示的面積。數據來源：Google。 ## 3.3 帶曲線軸的坐標系 到目前為止，我們遇到的所有坐標系都使用了兩個相互成直角的直軸，即使這些軸本身也建立了從數據值到位置的非線性映射。然而，還有其他坐標系，其中軸本身是彎曲的。特別是，在極坐標系中，我們通過角度和到原點的徑向距離來指定位置，因此角度軸是圓形的（圖 3.9）。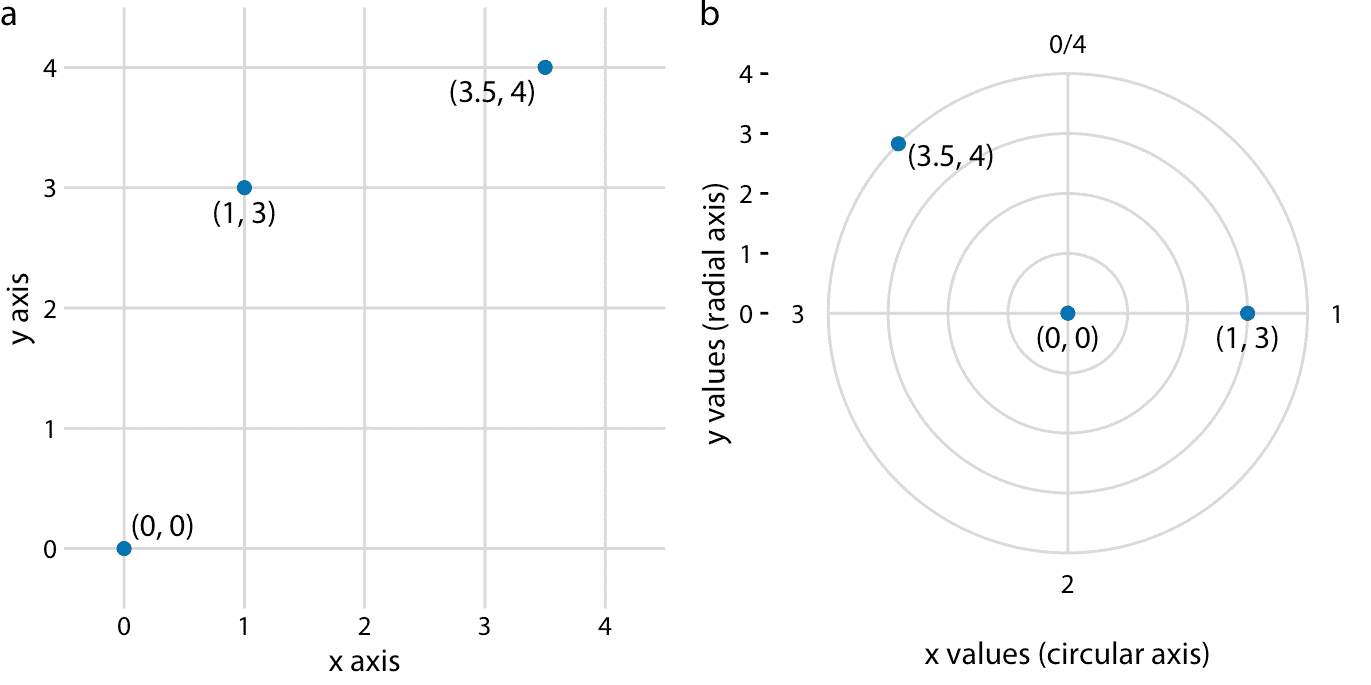  圖 3.9：笛卡爾坐標和極坐標之間的關系。 （a）笛卡爾坐標系中顯示的三個數據點。 （b）極坐標系中顯示的相同三個數據點。我們從（a）部分取 *x* 坐標并將它們用作角坐標，并將來自（a）部分的 *y* 坐標用作徑向坐標。在該示例中，圓軸從 0 到 4，因此 *x* = 0 和 *x* = 4 是該坐標系中的相同位置。 極坐標對于周期性數據可能是有用的，使得刻度一端的數據值可以從邏輯上連接到另一端的數據值。例如，考慮一年中的天數。 12 月 31 日是一年中的最后一天，但它也是一年中第一天的前一天。如果我們想要顯示一年中某些數量的變化，那么使用極坐標系和指定為日期的角度坐標是合適的。讓我們將這個概念應用于圖 2.3 的平均溫度。因為平均溫度是與任何特定年份無關的平均溫度，12 月 31 日可以被認為比 1 月 1 日晚 366 天（平均溫度包括 2 月 29 日）以及早一天。通過在極坐標系中繪制平均溫度，我們強調它們具有的這種周期特性（圖 3.10）。與圖 2.3 相比，極坐標版本突出了死亡谷，休斯頓和圣地亞哥從秋末到早春的溫度。在笛卡爾坐標系中，這個事實是模糊的，因為 12 月下旬和 1 月初的溫度值顯示在圖的不同部分，因此不形成單個視覺單元。  圖 3.10：美國四個選定位置的日平均溫度，以極坐標顯示。到中心點的徑向距離表示平均溫度（華氏），一年中的日期從 1 月 1 日開始在六點鐘位置逆時針排列。 我們遇到彎曲線軸的第二種情況是地理空間數據，即地圖。地球上的位置由其經度和緯度指定。但由于地球是一個球體，繪制緯度和經度作為笛卡爾軸是誤導和不推薦的（圖 3.11）。相反，我們使用各種類型的非線性投影，試圖最大限度地減少錯誤，并且相對于地球上真實形狀的線條，在保留面積或角度之間取得不同的平衡（圖 3.11）。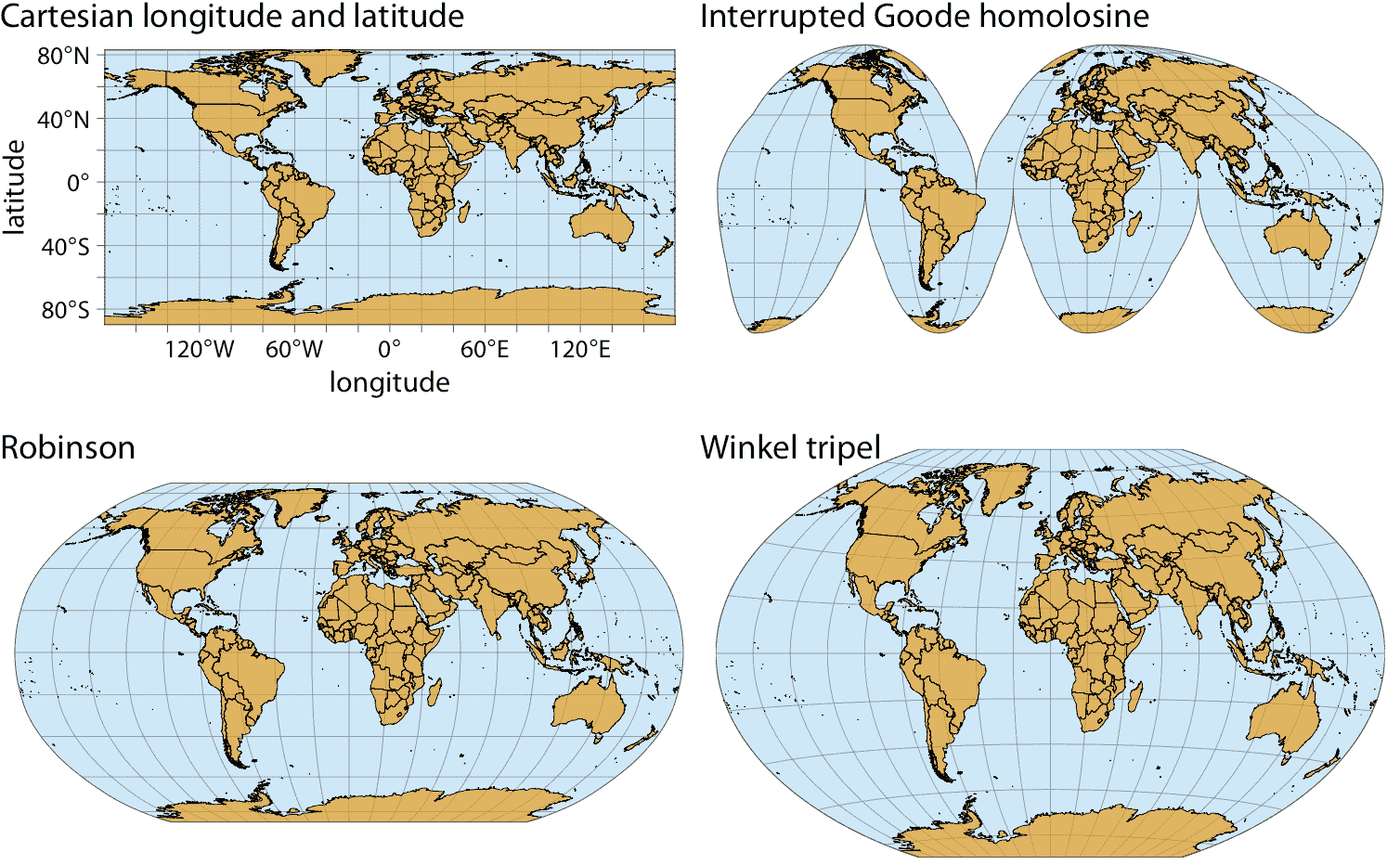  圖 3.11：世界地圖，以四種不同的投影顯示。笛卡爾經緯度系統將每個位置的經度和緯度映射到常規笛卡爾坐標系。該映射導致面積和角度相對于其在 3D 球體上的真實值的實質性失真。中斷的 Goode homolosine 投影完美地代表了真實的表面面積，代價是將一些陸塊分成單獨的部分，最著名的是格陵蘭島和南極洲。羅賓遜投影和 Winkel tripel 投影都在角度和面積扭曲之間取得平衡，它們通常用于整個地球的地圖。