# 9 一次可視化多個分布 > 原文： [9 Visualizing many distributions at once](https://serialmentor.com/dataviz/boxplots-violins.html) > 校驗：[飛龍](https://github.com/wizardforcel) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 在許多情況下，我們希望同時可視化多個分布。例如，考慮天氣數據。我們可能想要了解不同月份的溫度變化情況，同時還顯示每個月內觀測到的溫度分布。這種情況需要一次顯示 12 個溫度分布，每個月一個。在這種情況下，第七和八章中討論的所有可視化都不起作用。相反，可行的方法包括箱形圖，提琴圖和脊線圖。 每當我們處理許多分布時，根據響應變量和一個或多個分組變量進行思考是有幫助的。響應變量是我們想要顯示其分布的變量。分組變量定義具有響應變量的不同分布的數據的子集。例如，對于跨月的溫度分布，響應變量是溫度，分組變量是月。本章討論的所有技術都沿一個軸繪制響應變量，沿另一個軸繪制分組變量。在下文中，我將首先描述沿垂直軸顯示響應變量的方法，然后我將描述沿水平軸顯示響應變量的方法。在所討論的所有情況下，我們都可以翻轉軸并獲得另一種可行的可視化。我在這里展示了各種可視化的規范形式。 ## 9.1 沿垂直軸可視化分布 一次顯示多個分布的最簡單方法是將它們的平均值或中位數顯示為點，并通過誤差條顯示平均值或中值附近的變化。圖 9.1 將這種方法，用于展示 2016 年內布拉斯加州林肯市的月氣溫分布。我將此圖形標記為不好，因為這種方法存在多個問題。首先，通過僅用一個點和兩個誤差條表示每個分布，我們丟失了大量的數據信息。其次，即使大多數讀者可能猜測它們代表均值或中位數，但這些點代表的東西并不是很明顯。第三，誤差條代表什么肯定不明顯。它們是否代表數據的標準差，均值的標準誤差，95% 置信區間或其他一些東西？沒有普遍接受的標準。通過閱讀圖 9.1 的圖標題，我們可以看到，它們在這里代表日平均溫度標準差的兩倍，意味著指示包含大約 95% 數據的范圍。但是，誤差條更常用于顯示標準誤差（或 95% 置信區間的標準誤差的兩倍），讀者很容易將標準誤差與標準差混淆。標準誤差量化了我們對均值估計的準確程度，而標準差則估計了數據在均值周圍的分散程度。數據集可能具有非常小的均值標準誤差和非常大的標準差。第四，如果數據存在任何偏差，對稱誤差線會產生誤導，這種情況幾乎適用于所有真實世界的數據集。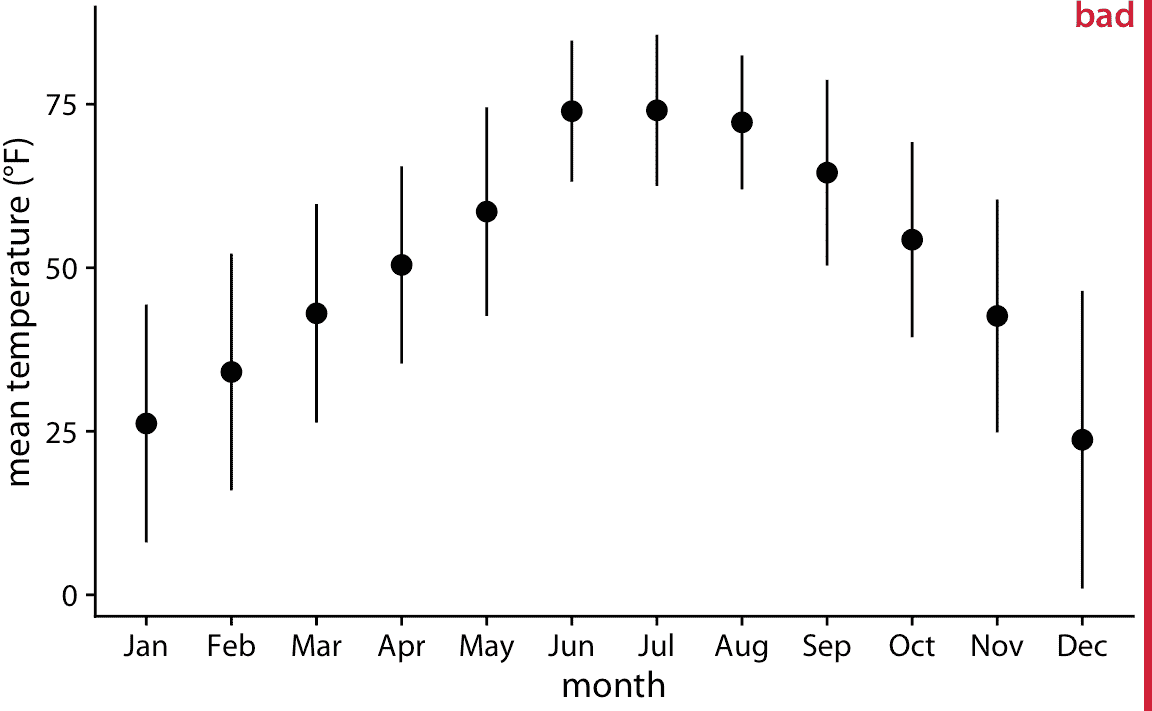  圖 9.1：2016 年內布拉斯加州林肯市的日平均氣溫。點表示每月的日平均溫度，在一個月的所有日期上計算平均，誤差條代表每個月的日平均溫度的兩倍標準差。這個圖形被標記為“不好”，因為誤差條通常用于顯示估計值的不確定性，而不是總體的可變性。數據來源：Weather Underground 我們可以通過使用傳統且常用的可視化分布方法（箱形圖）來解決圖 9.1 的所有四個缺點。箱形圖將數據劃分為四分位數并以標準化方式將其可視化（圖 9.2 ）。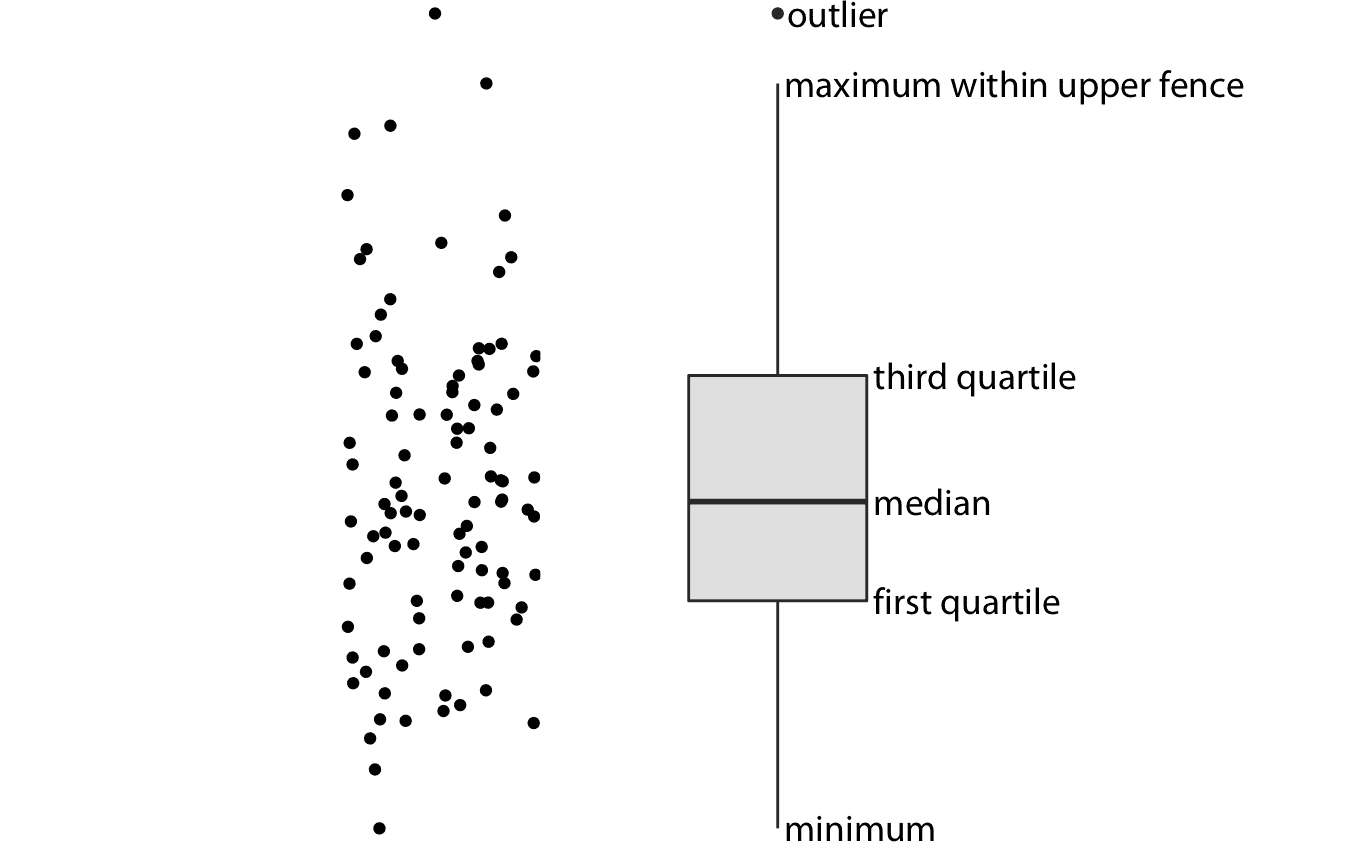  圖 9.2：箱形圖的剖析。顯示的是點云（左）和相應的箱形圖（右）。只有點的 *y* 值在箱線圖中可視化。箱形圖中間的線表示中位數，箱中包含 50% 的中間數據。頂部和底部的線延伸到數據的最大值和最小值，或者延伸到箱子高度的 1.5 倍以內的最大值或最小值，以較短的線為準。在任一方向上箱子高度的 1.5 倍的距離稱為上圍欄和下圍欄。超出圍欄的單個數據點稱為異常值，通常顯示為單個點。 箱形圖是簡單但信息豐富的，并且它們在彼此相鄰繪制，并一次可視化許多分布時，可以工作得很好。對于林肯溫度數據，使用箱線圖產生圖 9.3 。在該圖中，我們現在可以看到 12 月的溫度高度偏斜（大多數日子是中度冷，有些是非常寒冷），并且在其他幾個月（例如 7 月份）根本沒有偏斜。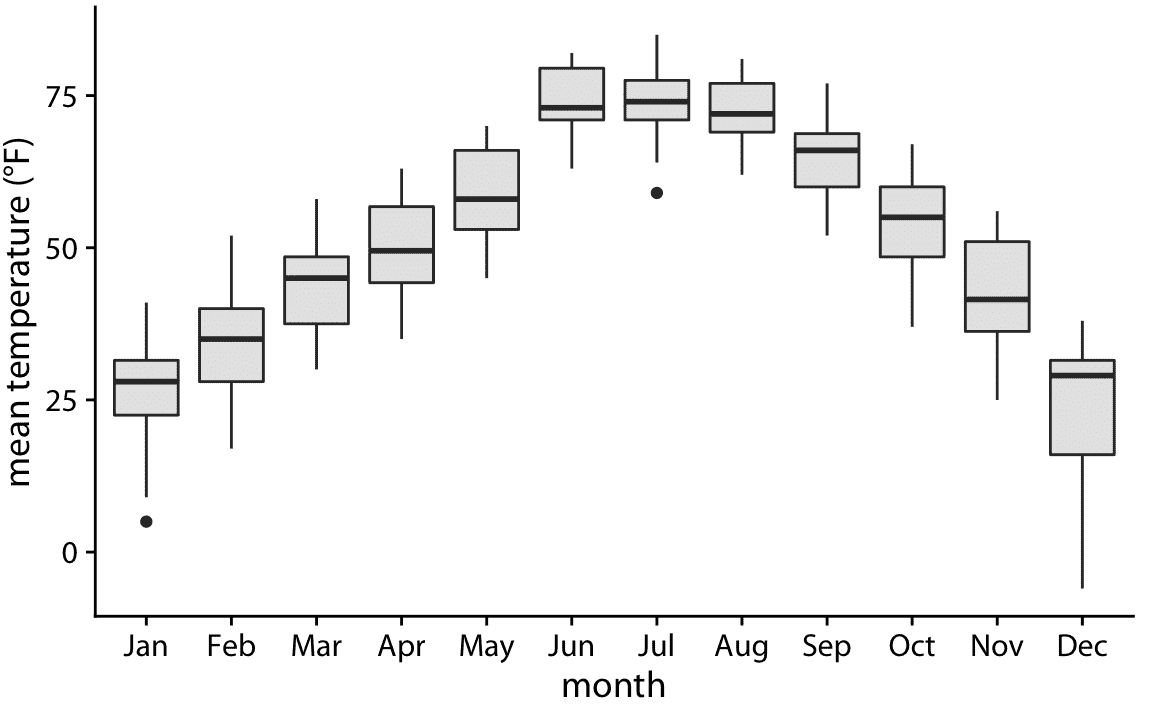  圖 9.3：內布拉斯加州林肯市的日平均溫度，可視化為箱線圖。 箱形圖是由統計學家 John Tukey 在 20 世紀 70 年代早期發明的，并且很快就受到歡迎，因為它們具有很高的信息量而且易于手工繪制。那時的大多數數據可視化都是手工繪制的。但是，憑借現代計算和可視化功能，我們不僅限于手工繪制的內容。因此，最近，我們看到箱形圖被提琴圖取代，這相當于第 7 章中討論的密度估計，但旋轉了 90 度然后生成鏡像（圖 9.4 ）。無論何時箱形都可以換成提琴圖，并且它們提供了更加細致的數據圖像。特別是，提琴圖將準確地表示雙峰數據，而箱形圖則不會。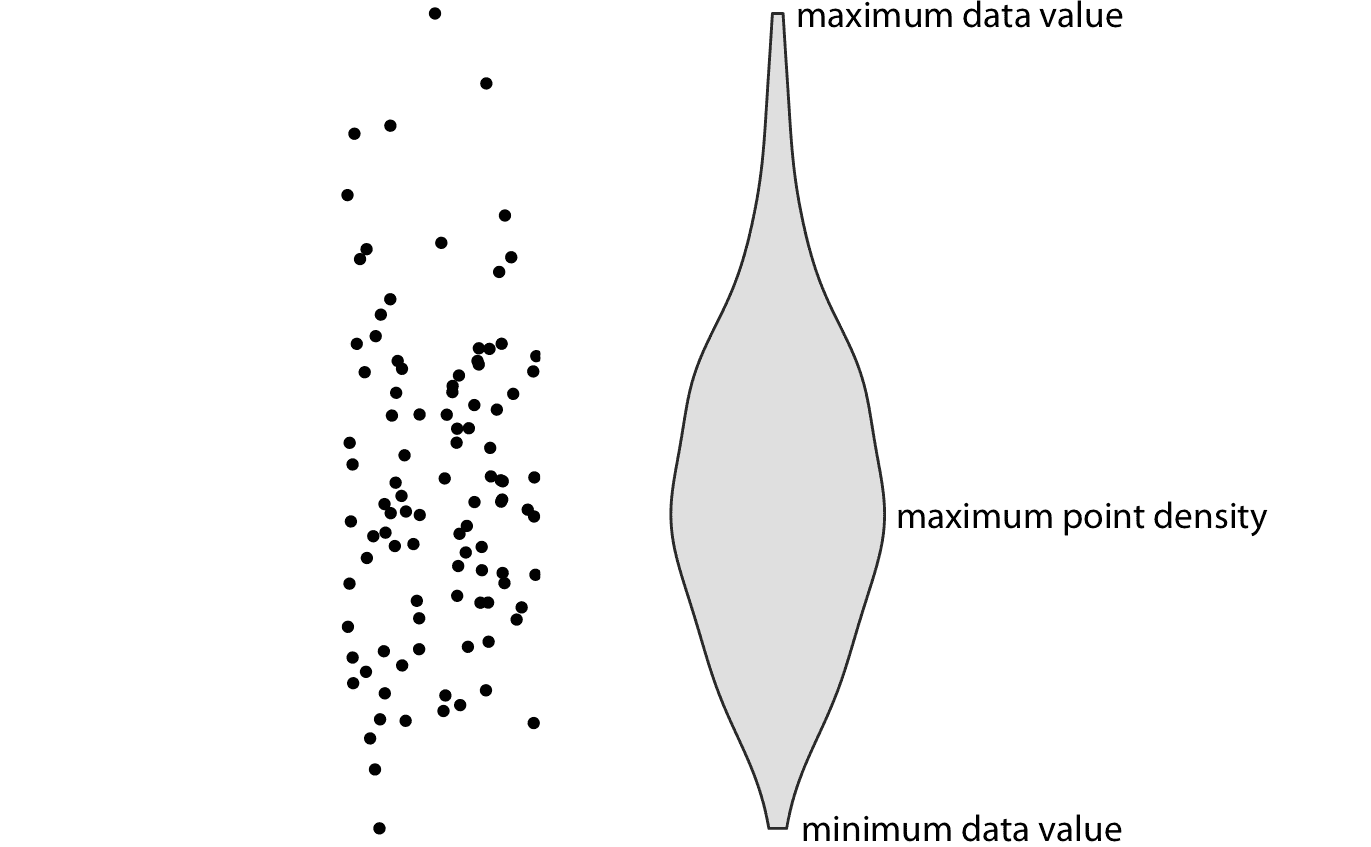  圖 9.4：提琴圖的剖析。顯示的是一團點（左）和相應的提琴圖（右）。只有點的 *y* 值在提琴圖中可視化。給定 *y* 值處的提琴寬度表示 *y* 值處的點密度。從技術上講，提琴曲線是一個旋轉 90 度然后鏡像的密度估計。因此提琴是對稱的。提琴分別以最小數據值開始，最大數據值結束。提琴最厚的部分對應于數據集中的最大點密度。 在使用提琴圖可視化分布之前，請確認每組中有足夠多的數據點，以便點密度為平滑線。 當我們用提琴圖顯示林肯溫度數據時，我們得到圖 9.5 。我們現在可以看到，幾個月確實有適度的雙峰數據。例如，11 月似乎有兩個溫度峰值，一個約 50 度，一個約 35 華氏度。  圖 9.5：內布拉斯加州林肯市的平均日氣溫，可視化為提琴曲線。 因為提琴圖是從密度估計得出的，所以它們也有類似的缺點（第七章）。特別是，它們可以在數據不存在的位置生成數據外觀，或者實際上數據集非常稀疏時數據集非常密集。我們可以嘗試通過簡單地直接繪制所有單個數據點來避免這些問題，如圖 9.6 。這樣的圖稱為帶狀圖。帶狀圖原則上很好，只要我們確保我們不會在彼此之上繪制太多的點。過度繪制的簡單解決方案是通過在 *x* 維度中添加一些隨機噪聲（圖 9.7），在 *x* 軸上使點稍微分散。這種技術也被稱為抖動。  圖 9.6：內布拉斯加州林肯市的日平均溫度，可視化為帶狀圖。每個點代表一天的平均溫度。這個圖形被標記為“不好”，因為很多點相互疊加，因此不可能確定每個月最常見的溫度。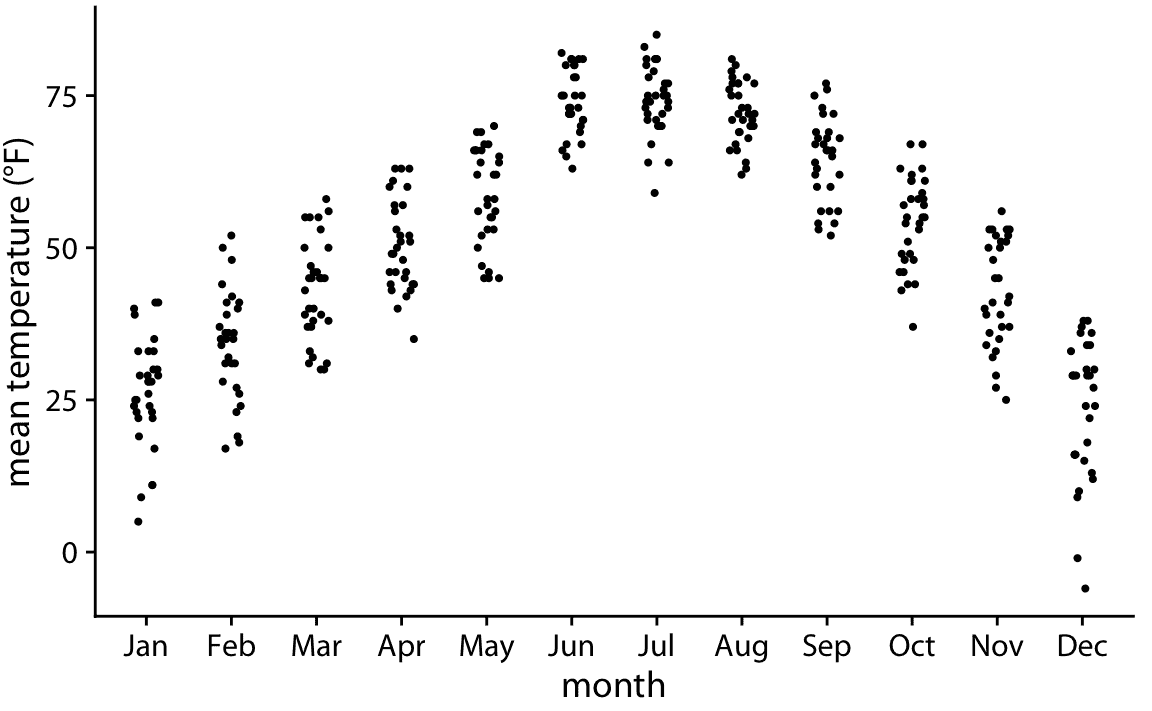  圖 9.7：內布拉斯加州林肯市的日平均溫度，可視化為帶狀圖。這些點沿 *x* 軸分散，以便更好地顯示每個溫度值的點密度。 每當數據集太稀疏而無法證明提琴可視化時，可以將原始數據繪制為單獨的點。 最后，通過在給定 *y* 坐標處，將點與點密度成比例散開，我們可以組合兩個圖的優勢。這種方法，稱為 sina 圖（Sidiropoulos 等 2018），可以被認為是提琴圖和展開點之間的混合，它顯示每個單獨的點，同時也可視化分布。我在這里在提琴之上繪制了 Sina 圖，以突出這兩種方法之間的關系（圖 9.8）。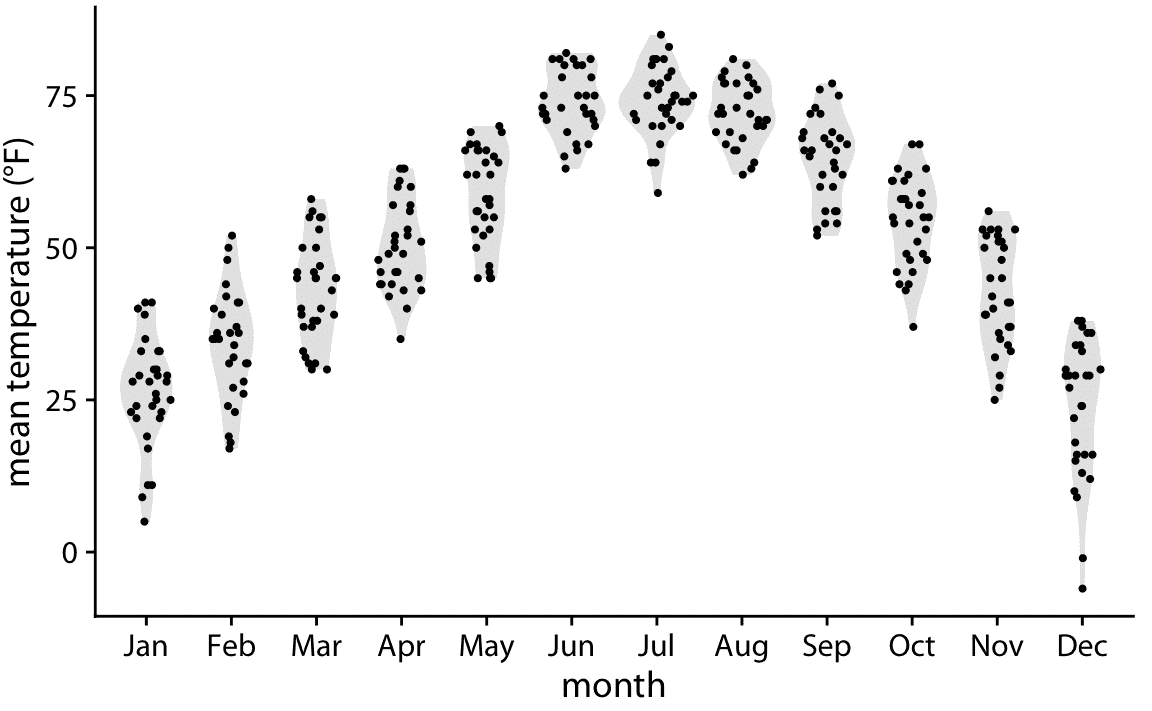  圖 9.8：內布拉斯加州林肯市的日平均氣溫，可視化為 Sina 陰影（單獨的點和提琴的組合）。這些點沿著 *x* 軸與各個溫度下的點密度成比例地散開。名稱 Sina 圖旨在表彰丹麥哥本哈根大學的學生 Sina Hadi Sohi，他編寫了該大學研究人員制作此類圖形的第一版代碼（Frederik O. Bagger, personal communication）。 ## 9.2 沿水平軸可視化分布 在第七章中，我們使用直方圖和密度圖來沿水平軸顯示分布。在這里，我們將通過在垂直方向上錯開分布圖來擴展這個想法。由此產生的可視化稱為脊線圖，因為這些圖看起來像脊線。如果想要顯示隨時間變化的分布趨勢，脊線圖往往效果特別好。 標準脊線圖使用密度估計（圖 9.9 ）。它與提琴圖密切相關，但經常激發對數據的更直觀的理解。例如，11 月左右的 35 度和 50 華氏度的兩個溫度簇，在圖 9.9 中比圖 9.5 更加明顯。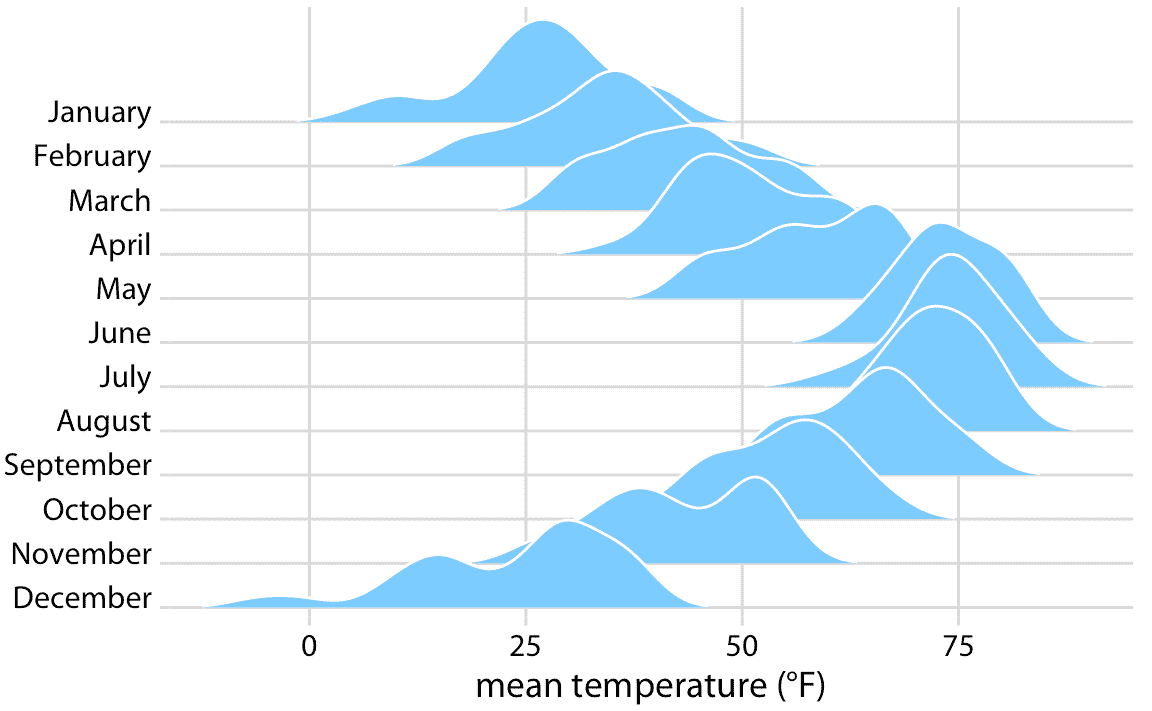  圖 9.9：2016 年內布拉斯加州林肯市的氣溫，可視化為脊線圖。對于每個月，我們以華氏度為單位顯示測量的日平均溫度的分布。原始圖概念： Wehrwein（2017）。 因為 *x* 軸顯示響應變量而 *y* 軸顯示分組變量，所以在脊線圖中沒有單獨的軸用于密度估計。密度估計與分組變量一起顯示。這與提琴圖沒有什么不同，其中密度也與分組變量一起顯示，沒有單獨的顯式刻度。在這兩種情況下，繪圖的目的不是顯示特定的密度值，而是為了便于比較各組的密度形狀和相對高度。 原則上，我們可以在脊線可視化中使用直方圖代替密度圖。但是，所得圖形通常看起來不太好（圖 9.10）。這些問題類似于堆疊或重疊的直方圖（第七章）。由于這些脊線直方圖中的垂直線始終顯示完全相同的 *x* 值，因此來自不同直方圖的條形以令人困惑的方式彼此對齊。在我看來，最好不要繪制這樣重疊的直方圖。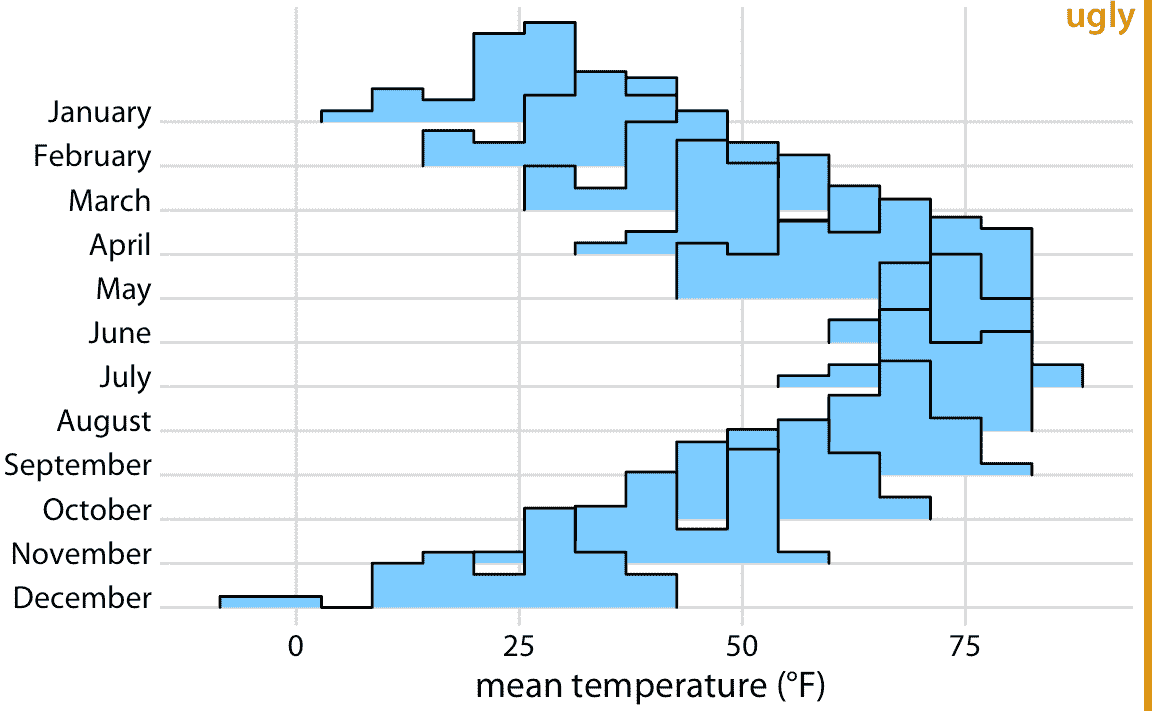  圖 9.10：2016 年內布拉斯加州林肯市的氣溫，可視化為直方圖的脊線圖。單個直方圖在視覺上不能很好地分離，整體圖形非常嘈雜且令人困惑。 脊線圖可以擴展到非常大的分布。例如，圖 9.11 顯示了從 1913 年到 2005 年的電影長度分布。該圖包含近 100 種不同的分布，但它很容易閱讀。我們可以看到，在 20 世紀 20 年代，電影有很多不同的長度，但自從大約 1960 年以來，電影長度標準化為大約 90 分鐘。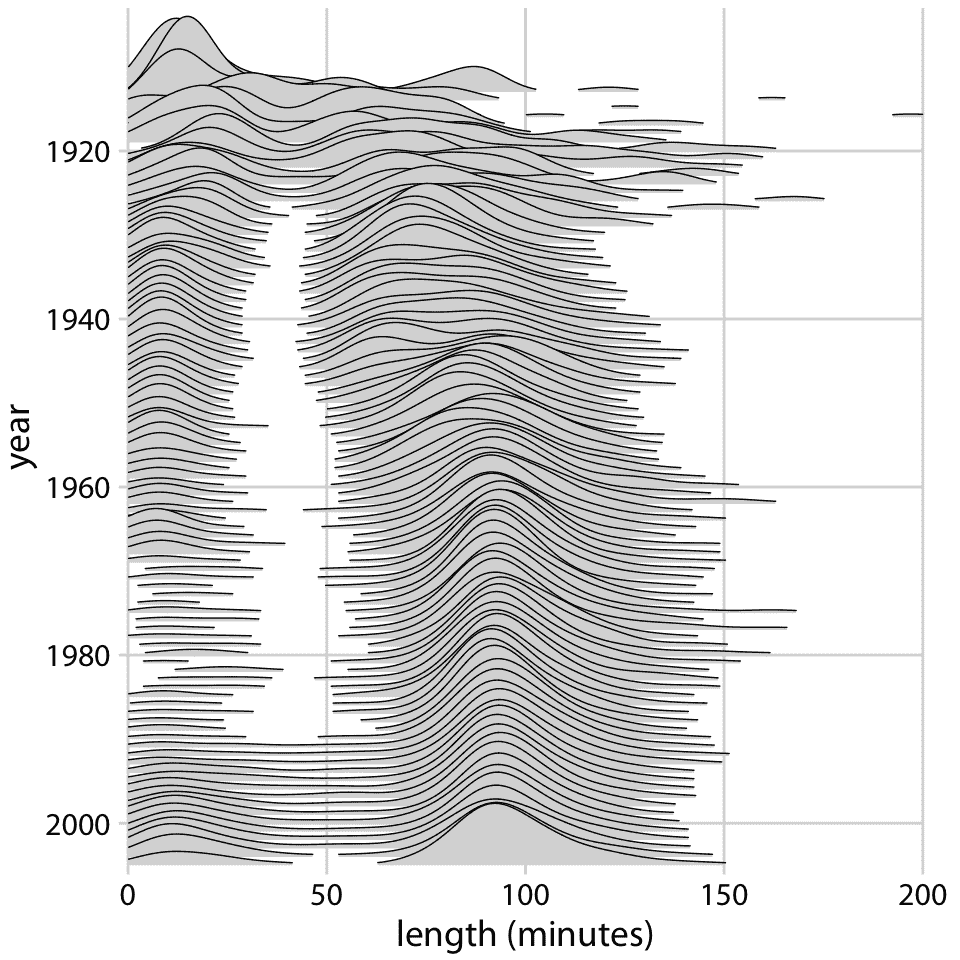  圖 9.11：電影長度隨時間的演變。自 20 世紀 60 年代以來，大部分電影都長約 90 分鐘。數據來源：互聯網電影數據庫，IMDB 如果我們想比較兩種趨勢，脊線圖也很有效。如果我們想要分析兩個不同黨派的成員的投票模式，則通常會出現這種情況。我們可以通過在時間上垂直交錯分布，并在每個時間點繪制兩個不同顏色的分布來進行比較，代表兩個黨派（圖 9.12 ）。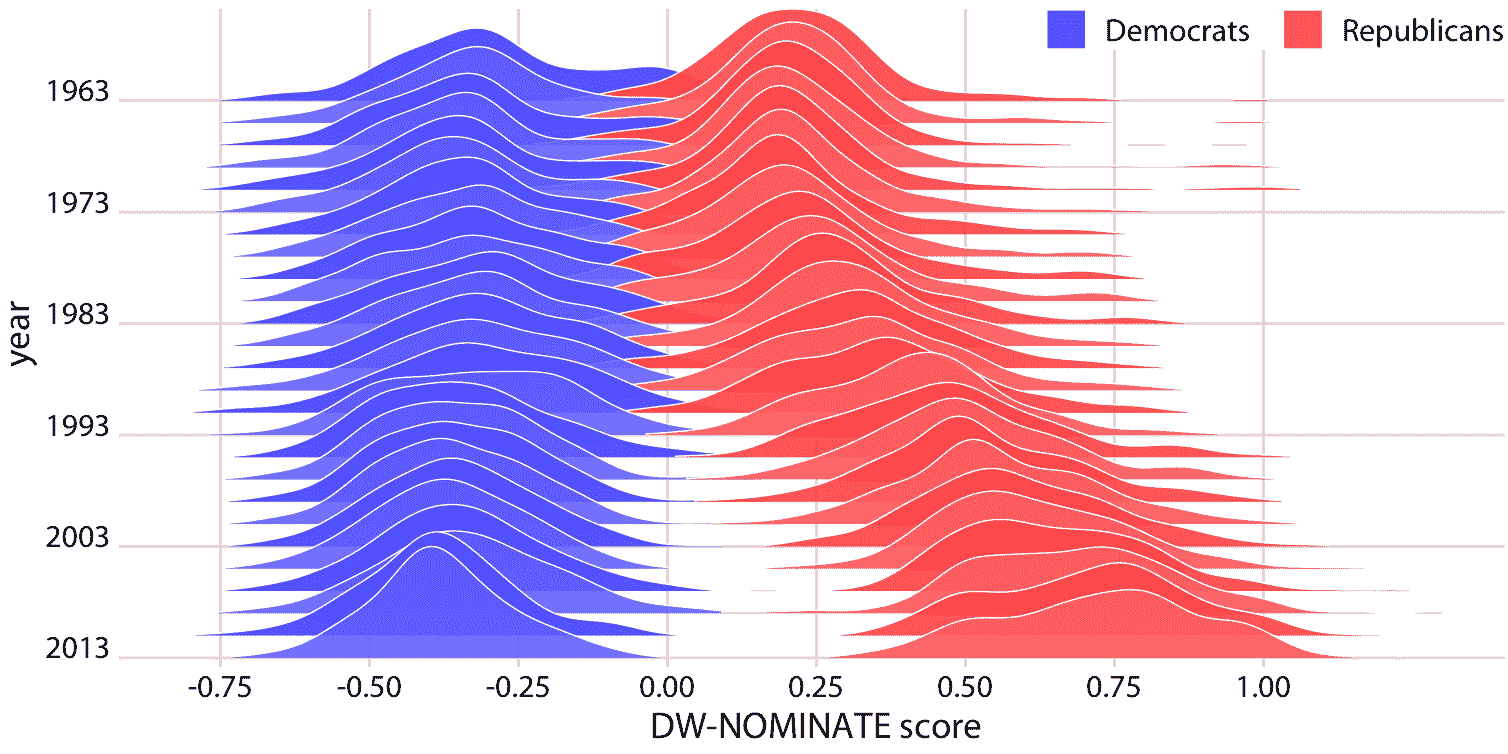  圖 9.12：美國眾議院的投票模式日益兩極分化。 DW-NOMINATE 分數經常用于比較各黨派之間的代表的投票模式，以及隨著時間的推移。對于 1963 年至 2013 年的每個國會，這里分別展示了民主黨人和共和黨人的分數分布。每個國會都由第一年表示。原圖概念：McDonald（2017）。 ### 參考 ``` Sidiropoulos, N., S. H. Sohi, T. L. Pedersen, B. T. Porse, O. Winther, N. Rapin, and F. O. Bagger. 2018. “SinaPlot: An Enhanced Chart for Simple and Truthful Representation of Single Observations over Multiple Classes.” J. Comp. Graph. Stat 27: 673–76. doi:10.1080/10618600.2017.1366914. Wehrwein, Austin. 2017. “It Brings Me Ggjoy.” http://austinwehrwein.com/data-visualization/it-brings-me-ggjoy/. McDonald, Ian. 2017. “DW-NOMINATE Using Ggjoy.” http://rpubs.com/ianrmcdonald/293304. ```