# 7 可視化分布：直方圖和密度圖 > 原文： [7 Visualizing distributions: Histograms and density plots](https://serialmentor.com/dataviz/histograms-density-plots.html) > 校驗：[飛龍](https://github.com/wizardforcel) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 我們經常遇到這樣的情況：我們想要了解特定變量在數據集中如何分布。舉一個具體的例子，我們將考慮泰坦尼克號的乘客，這是我們第六章中已經遇到的數據集。泰坦尼克號上有大約 1300 名乘客（不包括船員），我們已經報告了 756 名乘客的年齡。我們可能想知道，在泰坦尼克號上有什么年齡的多少乘客，即有多少兒童，年輕人，中年人，老年人等等。我們將乘客中不同年齡的相對比例稱為乘客的年齡分布。 ## 7.1 可視化單個分布 我們可以通過將所有乘客分組到具有可比年齡的箱子，然后計算每個箱中的乘客數量來獲得乘客的年齡分布的印象。該程序產生如表 7.1 的表格。 表 7.1: 泰坦尼克號上已知年齡的乘客數 | 年齡范圍 | 計數 | | --- | --- | | 0–5 | 36 | | 6–10 | 19 | | 11–15 | 18 | | 16–20 | 99 | | 21–25 | 139 | | 26–30 | 121 | | 31–35 | 76 | | 36–40 | 74 | | 41–45 | 54 | | 46–50 | 50 | | 51–55 | 26 | | 56–60 | 22 | | 61–65 | 16 | | 66–70 | 3 | | 71–75 | 3 | 我們可以通過繪制填充的矩形來顯示該表，這些矩形的高度對應于計數，其寬度對應于年齡段的寬度（圖 7.1）。這種可視化稱為直方圖。 （請注意，所有箱子必須具有相同的寬度，以便可視化成為有效的直方圖。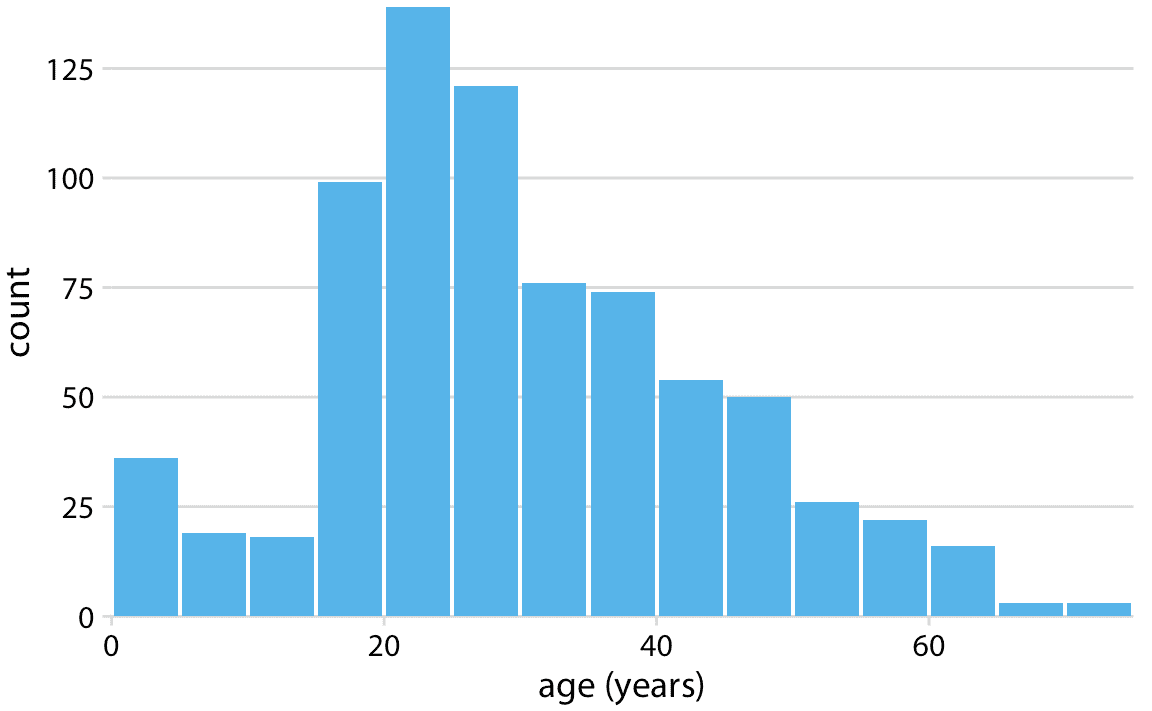）  圖 7.1：泰坦尼克號乘客年齡的直方圖。 因為直方圖通過對數據進行分箱而生成，所以它們的確切視覺外觀取決于箱寬的選擇。生成直方圖的大多數可視化程序默認選擇一個箱寬，但是對于您可能想要制作的任何直方圖，箱寬可能不是最合適的。因此，始終嘗試不同的箱寬來驗證所得直方圖是否準確反映基礎數據至關重要。通常，如果箱寬太小，則直方圖變得過于尖銳并且視覺上嘈雜，并且數據中的主要趨勢可能被掩蓋。另一方面，如果箱寬太大，則數據分布中的較小特征（例如 10 歲左右的下降）可能消失。 對于泰坦尼克號乘客的年齡分布，我們可以看到一歲的箱寬太小，十五歲的箱寬太大，而箱寬在三到五年之間最合適（圖 7.2）。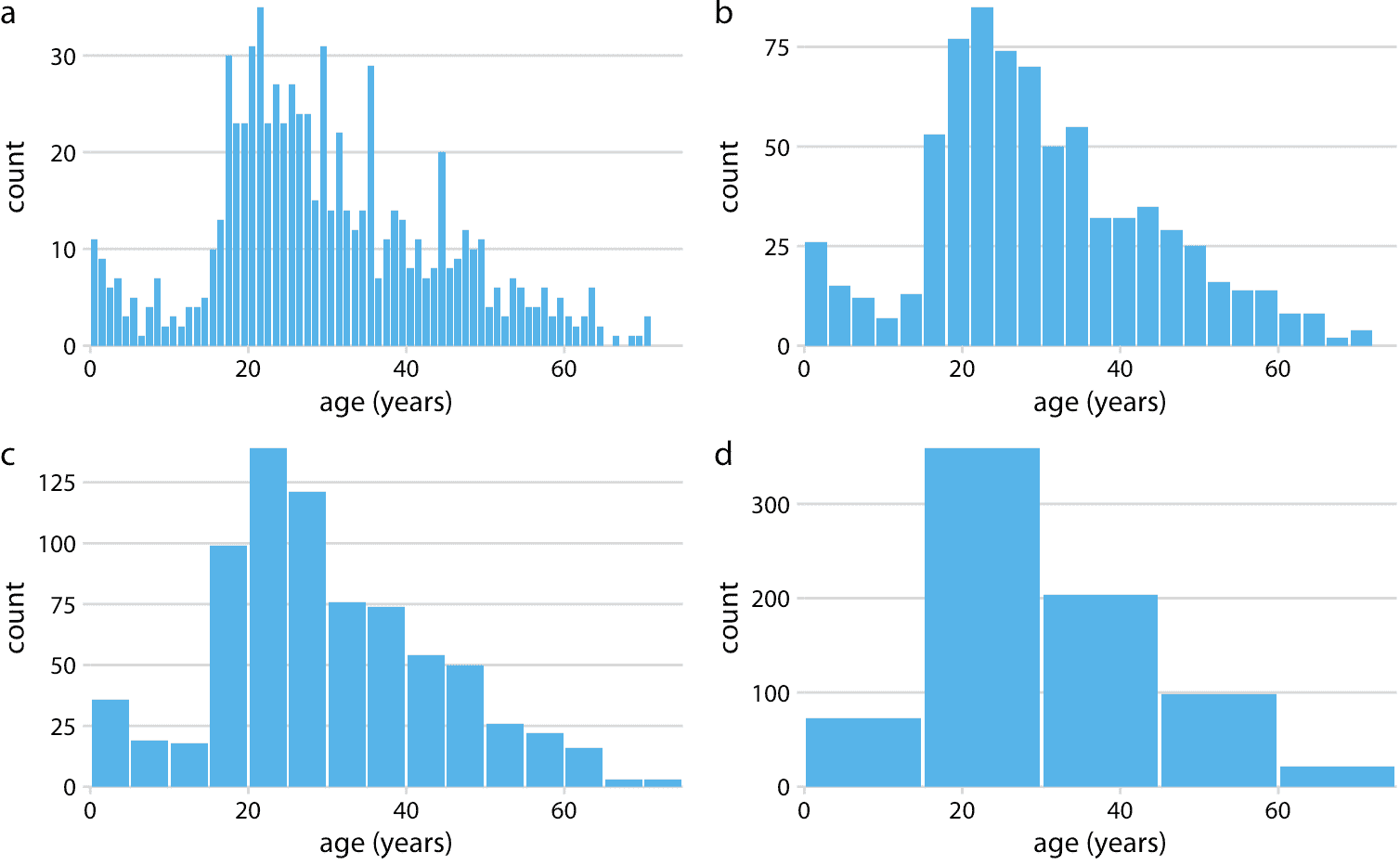  圖 7.2：直方圖取決于所選的箱寬。在這里，泰坦尼克號乘客的年齡分布相同，有四種不同的箱寬：（a）一歲; （b）三歲; （c）五歲; （d）十五歲。 制作直方圖時，請始終探索多個箱寬。 自至少 18 世紀以來，直方圖一直是流行的可視化選項，部分原因在于它們很容易通過手工生成。最近，由于筆記本電腦和手機等日常設備已經具備了廣泛的計算能力，我們發現它們越來越多地被密度圖取代。在密度圖中，我們嘗試通過繪制適當的連續曲線來顯示數據的基本概率分布（圖 7.3）。該曲線需要從數據中估計，并且用于該估計過程的最常用方法稱為核密度估計。在核密度估計中，我們在每個數據點的位置畫一個較小寬度（由一個名為帶寬的參數控制）的連續曲線（核），然后我們將所有這些曲線加起來以獲得最終密度估計。最廣泛使用的核是高斯核（即高斯鐘形曲線），但還有許多其他選擇。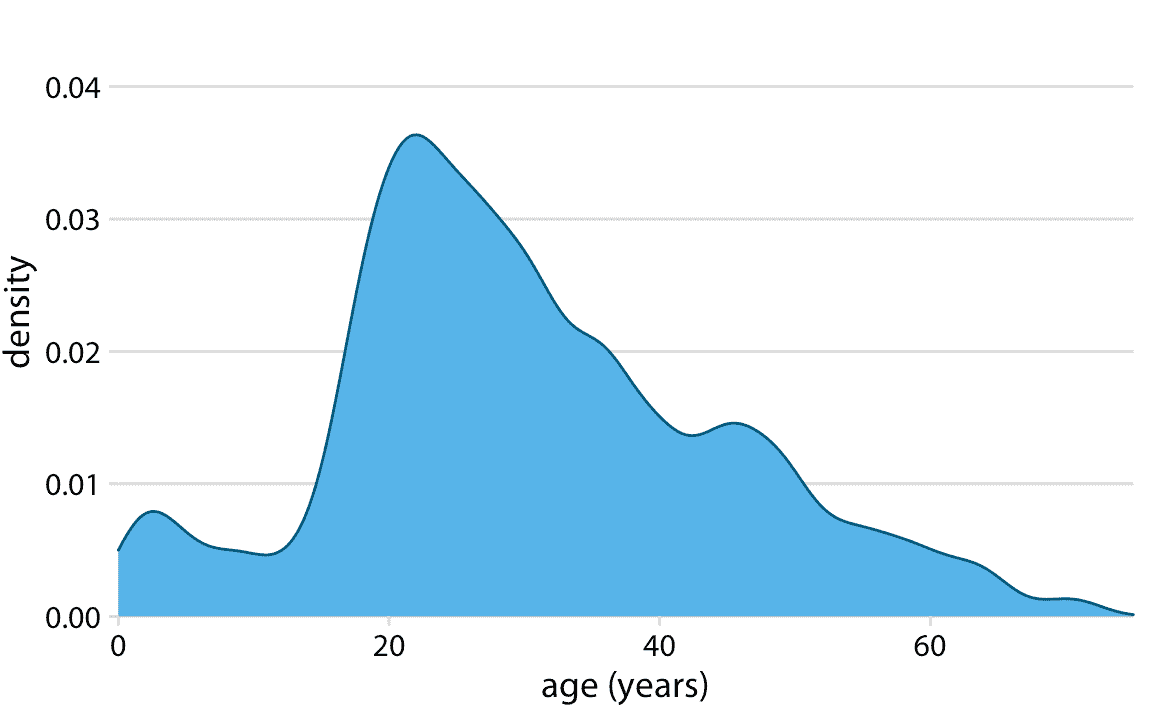  圖 7.3：泰坦尼克號上乘客年齡分布的核密度估計。縮放曲線的高度，使得曲線下面積等于 1。密度估計用高斯核實現，帶寬為 2。 與直方圖的情況一樣，密度圖的確切視覺外觀取決于核和帶寬選擇（圖 7.4 ）。帶寬參數的行為類似于直方圖中的箱寬。如果帶寬太小，則密度估計可能變得過于尖銳并且視覺上嘈雜，并且數據中的主要趨勢可能被掩蓋。另一方面，如果帶寬太大，則數據分布中的較小特征可能消失。此外，核的選擇會影響密度曲線的形狀。例如，高斯核將傾向于產生看起來像高斯的密度估計，具有平滑的特征和尾部。相比之下，矩形核可以在密度曲線中產生階梯形的外觀（圖 7.4d）。通常，數據集中的數據點越多，核的選擇就越少。因此，密度圖對于大型數據集來說往往是非常可靠和有用的信息，但對于只有幾個點的數據集可能會產生誤導。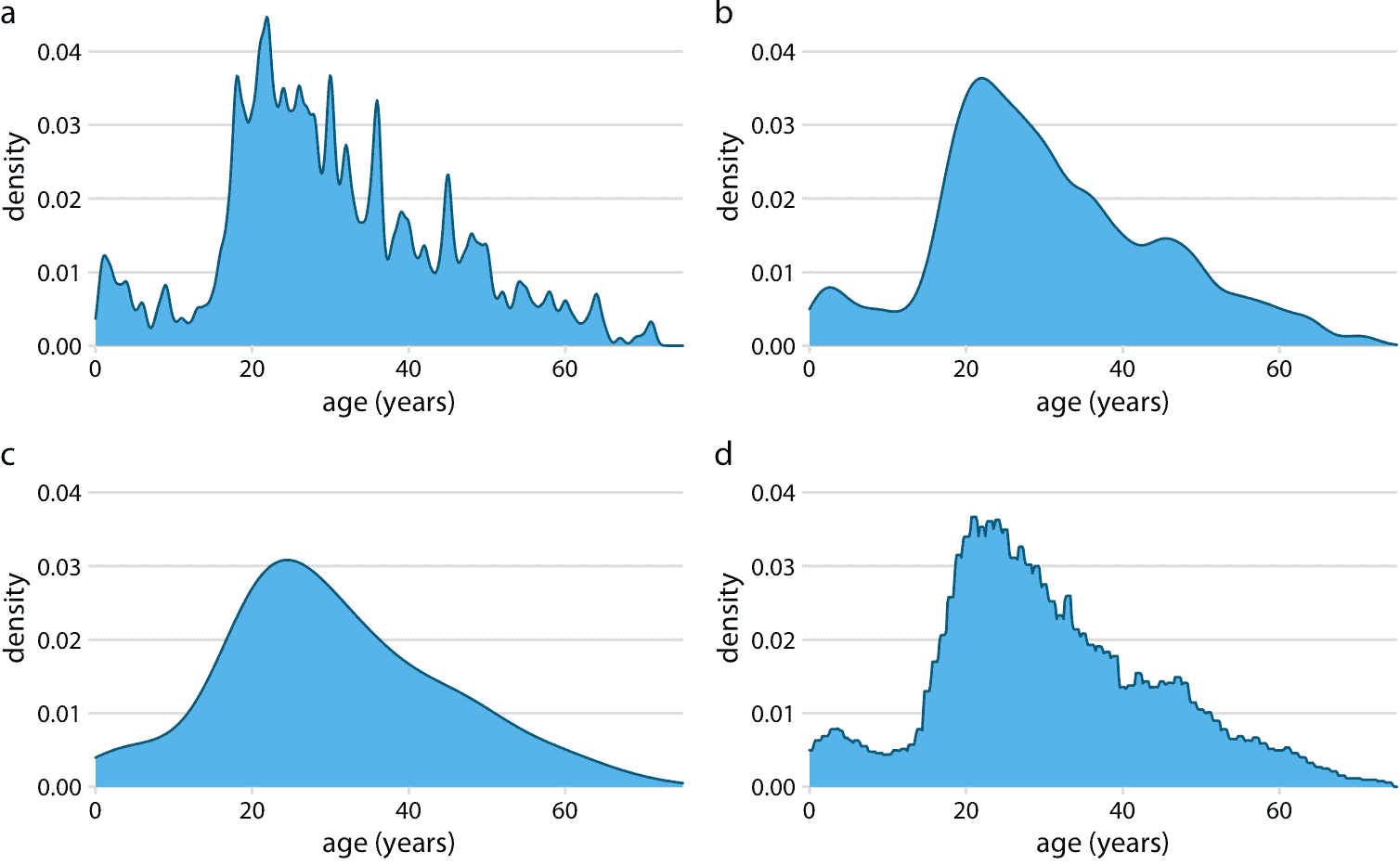  圖 7.4：核密度估計取決于所選的核和帶寬。這里，使用這些參數的四種不同組合顯示了泰坦尼克號乘客的相同年齡分布：（a）高斯核，帶寬 =0.5; （b）高斯核，帶寬 =2; （c）高斯核，帶寬 =5; （d）矩形核，帶寬 =2。 密度曲線通常按比例縮放，使得曲線下面積等于 1。這種慣例會使 *y* 軸刻度混亂，因為它取決于 *x* 軸的單位。例如，在年齡分布的情況下， *x* 軸上的數據范圍從 0 到大約 75。因此，我們期望密度曲線的平均高度為 1/75 = 0.013。實際上，當觀察年齡密度曲線時（例如，圖 7.4），我們看到 *y* 值的范圍從 0 到大約 0.04，平均值接近 0.01。 核密度估計有一個我們需要注意的陷阱：它們傾向于在不存在數據的地方產生數據外觀，特別是在尾部。因此，不小心使用密度估計很容易導致產生無意義的圖形。例如，如果我們不注意，我們可能會生成包含負年齡的年齡分布的可視化（圖 7.5）。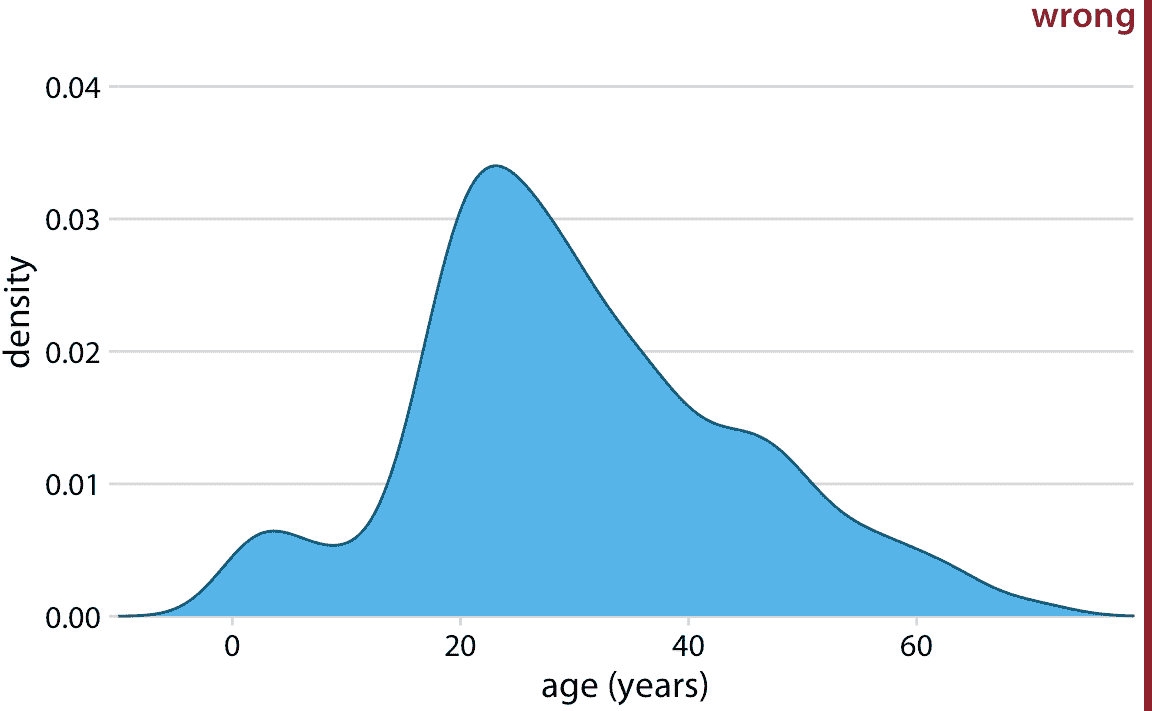  圖 7.5：核密度估計可以將分布的尾部擴展到沒有數據，甚至不可能存在數據的區域。在這里，密度估計已被允許延伸到負年齡范圍。這顯然是荒謬的，應該避免。 始終驗證您的密度估計沒有預測無意義數據值的存在。 那么你應該使用直方圖或密度圖來顯示分布嗎？可以就這個主題進行激烈的討論。有些人強烈反對密度圖，并認為它們是任意的和誤導性的。其他人意識到直方圖可能同樣具有任意性和誤導性。我認為選擇主要取決于品味，但有時候一個或另一個選項可能更準確地反映手頭數據中感興趣的具體特征。也有可能不使用二者，而是選擇經驗累積密度函數或 q-q 圖（第八章）。最后，我相信，一旦我們想要一次可視化多個分布，密度估計就會比直方圖具有固有的優勢（見下一節）。 ## 7.2 同時可視化多個分布 在許多情況下，我們有多個分布，我們希望同時可視化。例如，假設我們想看看泰坦尼克號乘客的年齡在男女之間如何分布。男性和女性乘客一般是同齡人，還是性別之間存在年齡差異？在這種情況下，一種常用的可視化策略是堆疊直方圖，我們在男性的條形上繪制不同顏色的女性直方圖條形（圖 7.6）。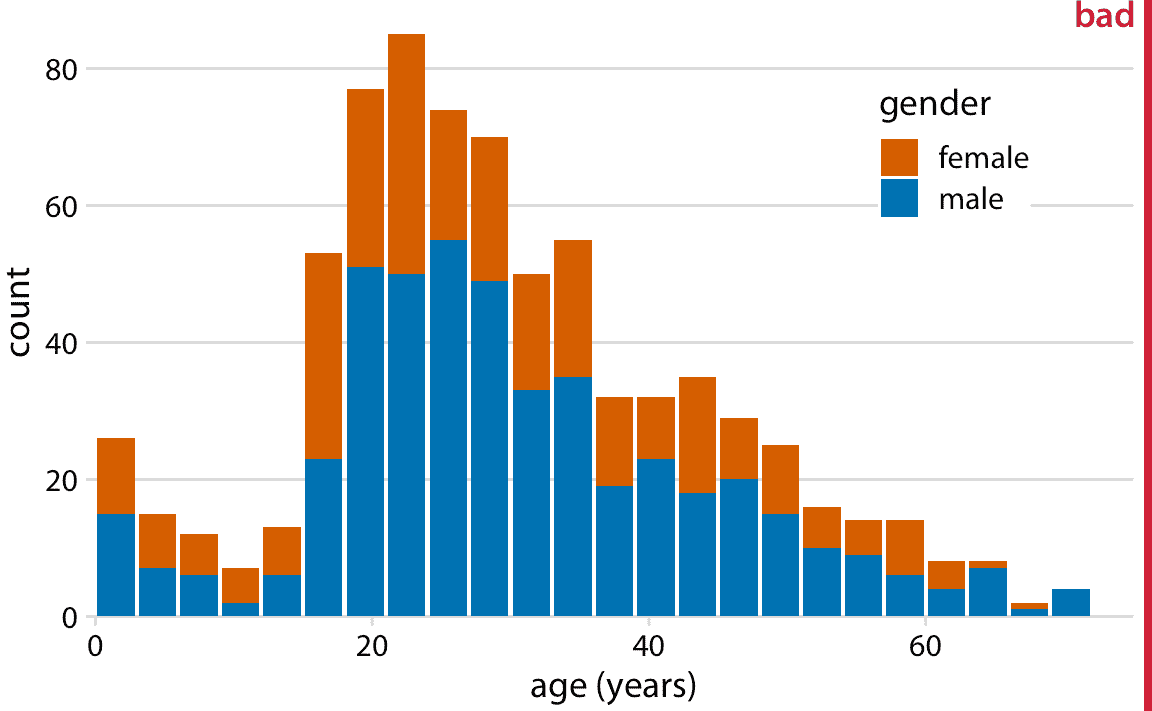  圖 7.6：按性別分層的泰坦尼克號乘客年齡的直方圖。這個圖形被標記為“不好”，因為堆疊的直方圖很容易與重疊的直方圖混淆（另見圖 7.7 ）。另外，代表女性乘客的條形的高度不容易彼此比較。 在我看來，應該避免這種類型的可視化。這里有兩個關鍵問題：首先，僅僅看一下這個圖形，不會完全清楚這些條形的確切位置。它們是從顏色變化開始還是從零開始？換句話說，是否有大約 25 位女性，年齡在 18-20 歲或者幾乎有 80 位？（前者就是這種情況。）其次，女性計數的高度不能直接相互比較，因為這些都是從不同高度開始的。例如，男性平均年齡大于女性，這一事實在圖 7.6 中根本不可見。 我們可以嘗試通過讓所有條形從零開始并使條形部分透明來解決這些問題（圖 7.7）。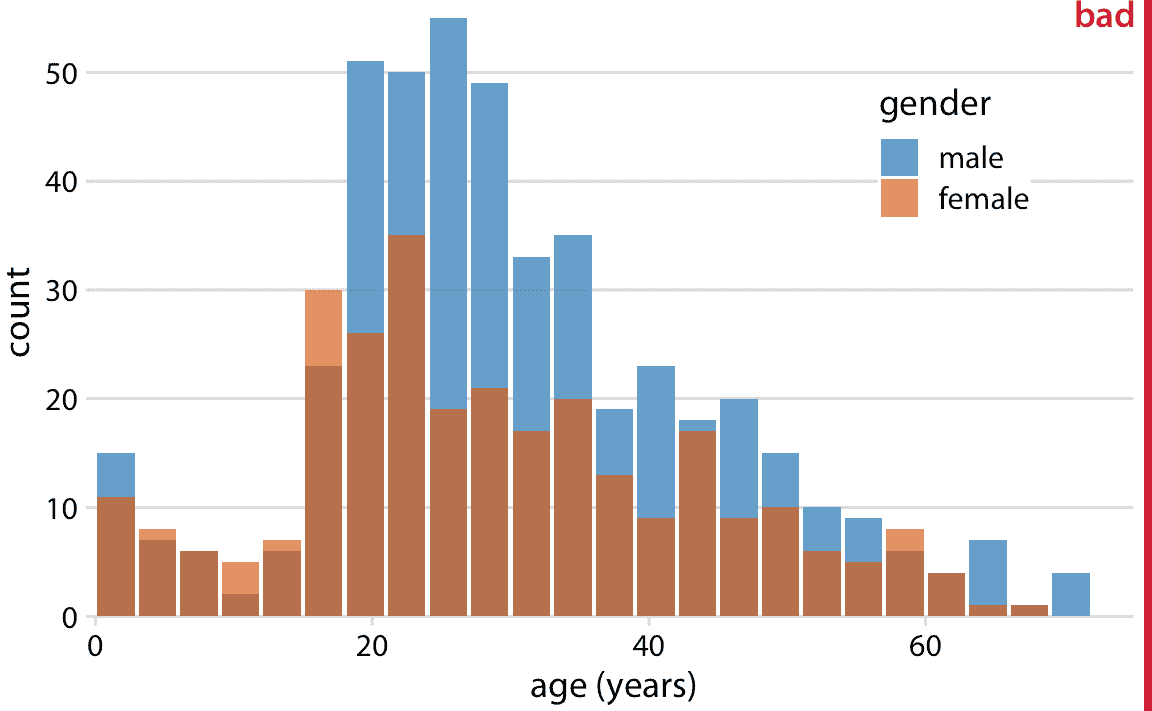  圖 7.7：男性和女性泰坦尼克號乘客的年齡分布，顯示為兩個重疊的直方圖。這個圖形被標記為“不好”，因為沒有明確的視覺指示，所有藍條都以 0 開始計數。 但是，這種方法會產生新的問題。現在看來實際上有三個不同的組，而不僅僅是兩組，我們仍然不完全確定每個條形的開始和結束位置。重疊的直方圖不能工作得很好，因為在另一個上面繪制的半透明條看起來不像半透明條形，而是像用不同顏色繪制的條形。 重疊密度圖通常不具有重疊直方圖所具有的問題，因為連續密度線有助于眼睛保持分布分離。然而，對于這個特定的數據集，男性和女性乘客的年齡分布在 17 歲左右幾乎相同，然后發散，因此產生的可視化仍然不理想（圖 7.8）。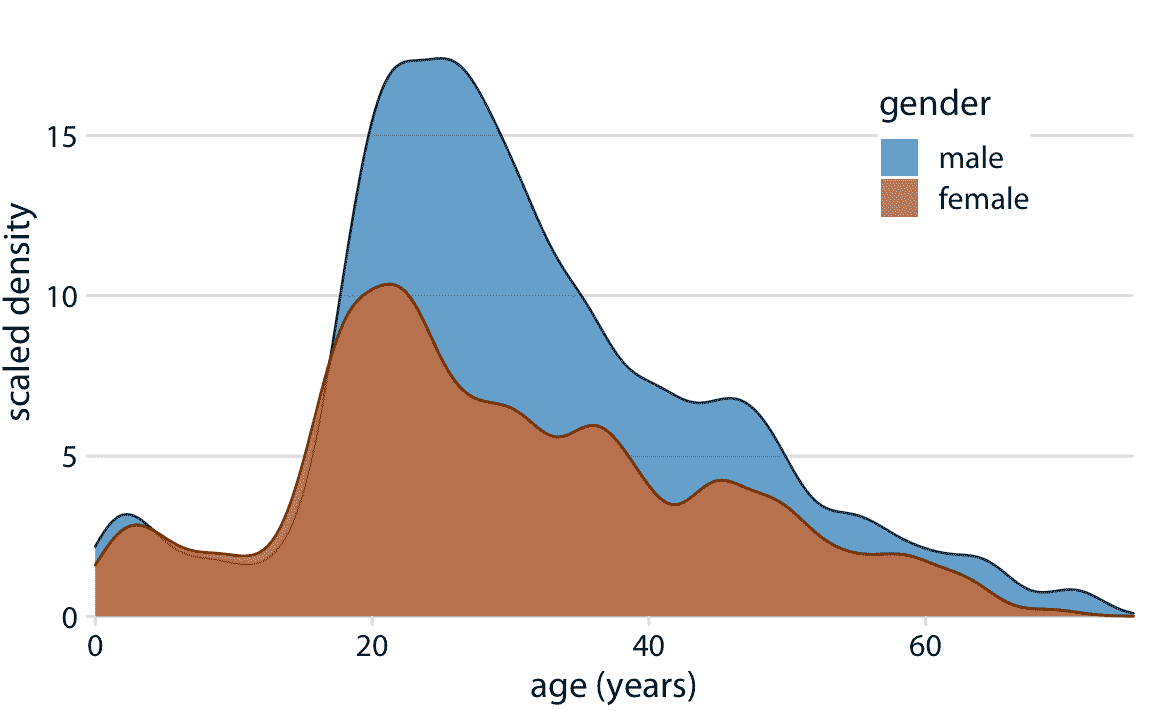  圖 7.8：男性和女性泰坦尼克號乘客年齡的密度估計。為了突出顯示男性乘客多于女性乘客，密度曲線按比例縮放，使得每條曲線下的面積對應于已知年齡的男性和女性乘客的總數（分別為 468 和 288）。 適用于該數據集的解決方案是分別顯示男性和女性乘客的年齡分布，每個圖作為整體年齡分布的一個比例（圖 7.9）。這種可視化直觀而清晰地表明，在泰坦尼克號上，20-50 歲年齡段的女性比男性少得多。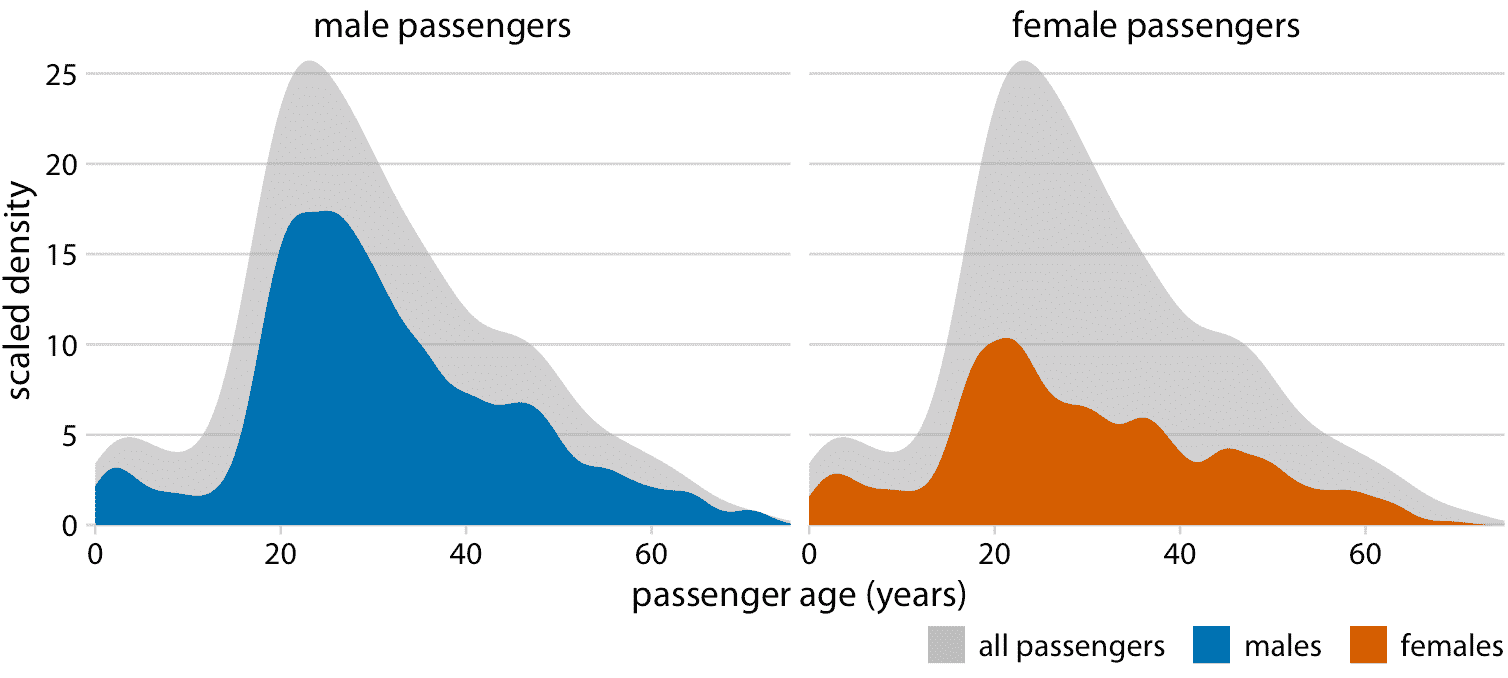  圖 7.9：男性和女性泰坦尼克號乘客的年齡分布，以乘客總數的比例顯示。彩色區域分別顯示男性和女性乘客年齡的密度估計，灰色區域顯示乘客整體年齡分布。 最后，當我們想要準確地可視化兩個分布時，我們還可以制作兩個單獨的直方圖，將它們旋轉 90 度，并使一個直方圖中的條形指向另一個直方圖的相反方向。這種技巧通常用于可視化年齡分布，結果圖通常稱為年齡金字塔（圖 7.10）。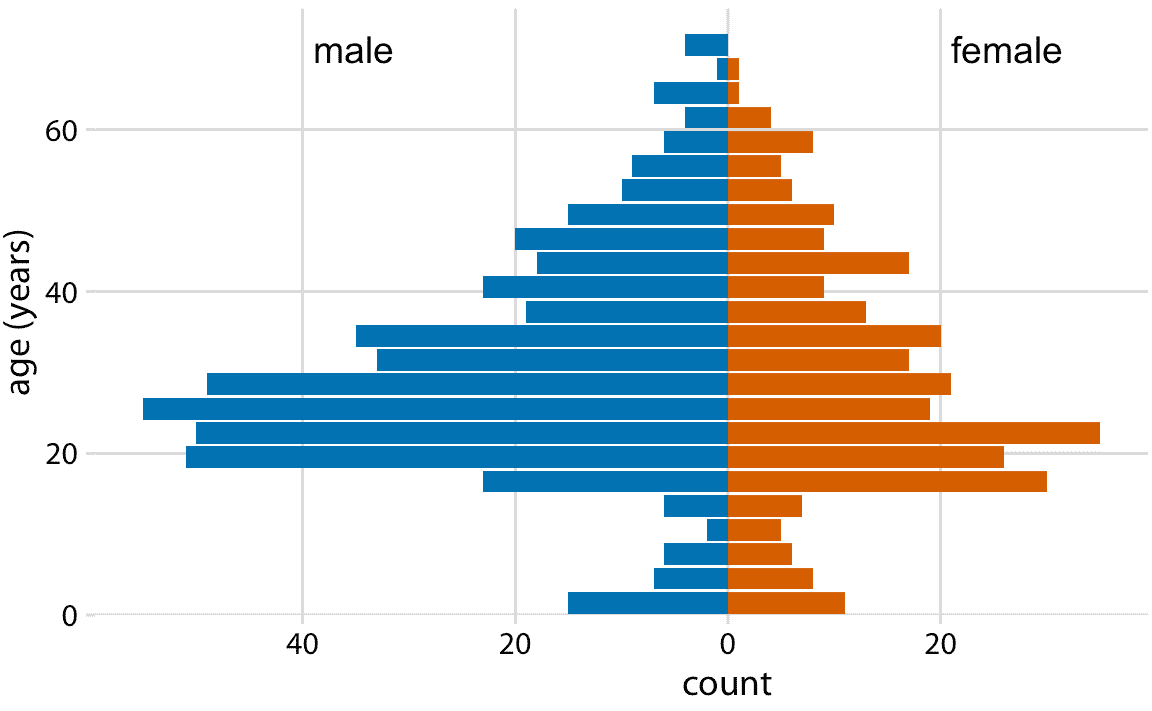  圖 7.10：可視化為年齡金字塔的男性和女性泰坦尼克號乘客的年齡分布。 重要的是，當我們想要同時顯示兩個以上的分布時，這個技巧不起作用。對于多個分布，直方圖往往變得高度混亂，而密度圖只要分布有些不同且連續就能工作得很好。例如，為了可視化來自四個不同品種的奶牛的乳脂百分比分布，密度圖很好（圖 7.11）。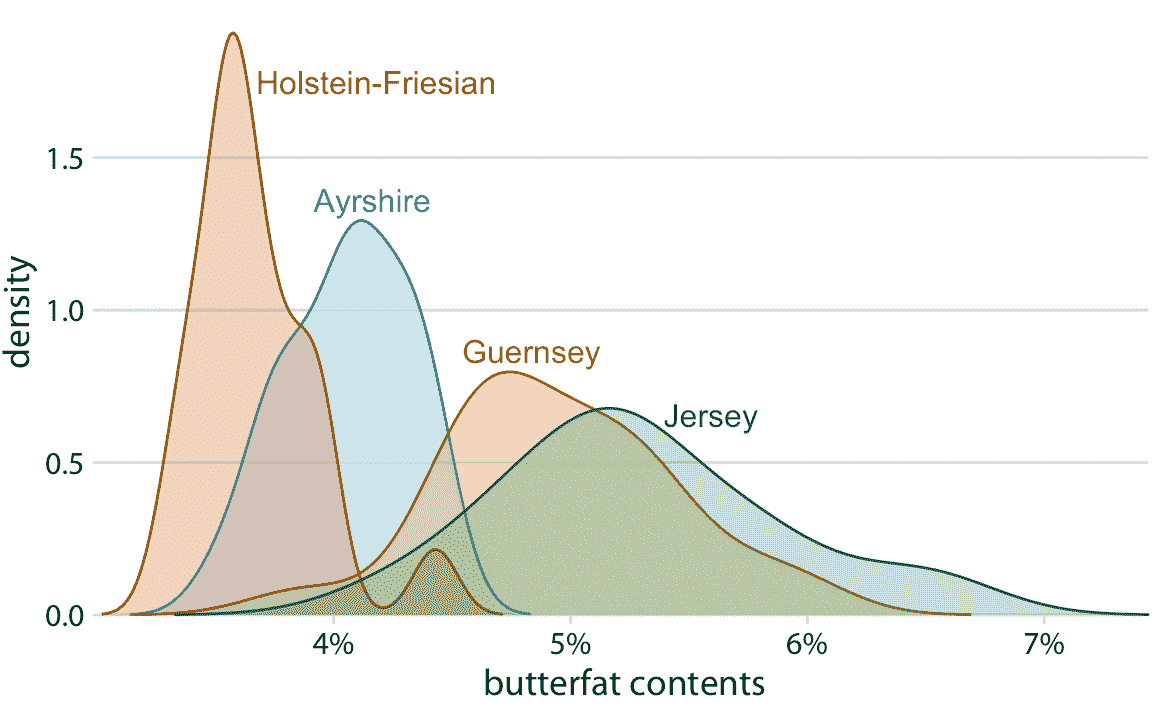  圖 7.11：四個品種的牛奶中乳脂百分比的密度估計。數據來源：加拿大純種奶牛的表現記錄 為了一次可視化幾個分布，核密度圖通常比直方圖更好。