# 12 可視化兩個或多個定量變量之間的關聯 > 原文： [12 Visualizing associations among two or more quantitative variables](https://serialmentor.com/dataviz/visualizing-associations.html) > 校驗：[飛龍](https://github.com/wizardforcel) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 許多數據集包含兩個或更多個定量變量，我們可能對這些變量如何相互關聯感興趣。例如，我們可能有一個不同動物的量化測量值數據集，例如動物的身高，體重，長度和日常能量需求。僅繪制兩個這樣的變量的關系，例如：身高和體重，我們通常會使用散點圖。如果我們想一次顯示兩個以上的變量，我們可能會選擇氣泡圖，散點圖矩陣或相關圖。最后，對于非常高維的數據集，執行降維可能是有用的，例如以主成分分析的形式。 ## 12.1 散點圖 我將使用在 123 只藍色杰伊鳥上進行的測量值數據集，來演示基本散點圖及其若干變體。數據集包含每只鳥的頭部長度（從頭部的尖端到頭部后部測量），頭骨大小（頭部長度減去喙部長度）以及體重等信息。我們希望這些變量之間存在關系。例如，具有較長喙部的鳥類預計具有較大的頭骨大小，具有較大體重的鳥類應具有比具有較小體重的鳥類更大的喙部和頭骨。 為了探索這些關系，我先從頭部長度與體重的關系圖開始（圖 12.1）。在該圖中，頭長度沿 *y* 軸顯示，體重沿 *x* 軸顯示，每只鳥用一個點表示。 （注意術語：我們說，我們根據沿 *x* 軸顯示的變量繪制沿 *y* 軸顯示的變量。）點形成一個分散的云（因此術語是散點圖），但毫無疑問，一個趨勢是，體重較大的鳥類有更長的頭部。頭部最長的鳥接近觀察到的最大體重，頭部最短的鳥接近觀察到的最小體重。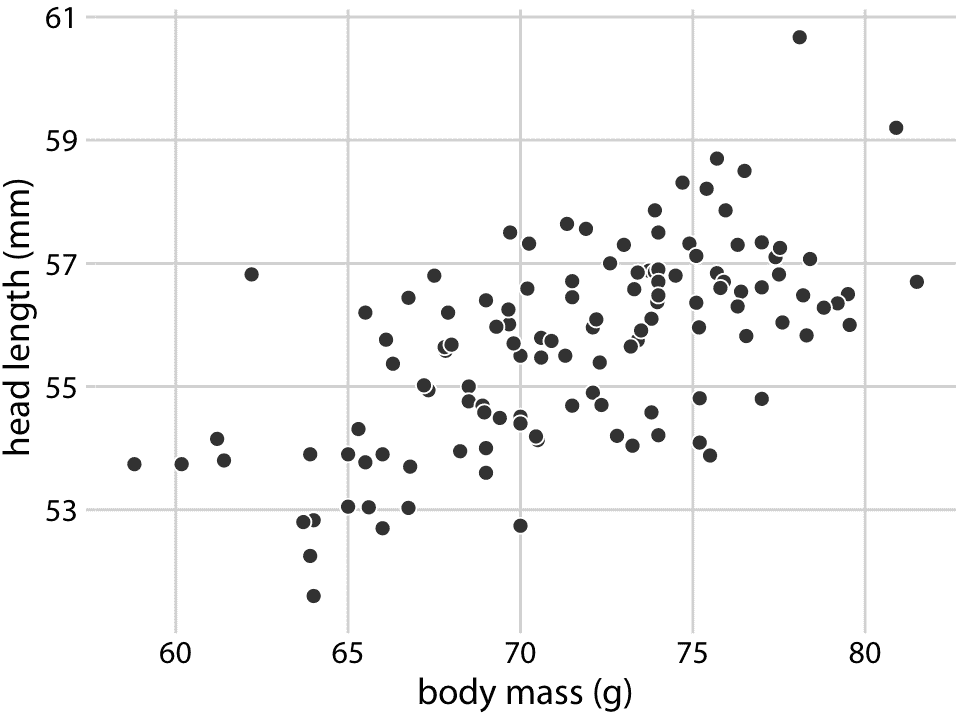  圖 12.1：頭部長度（從喙部尖端到頭部后部測量，單位為 mm）與體重（以克為單位），123 個藍顏色刻度記。每個點對應一只鳥。傾向是較重的鳥類有較長的頭部。數據來源：歐柏林學院的 Keith Tarvin 藍色杰伊數據集鳥包含雄鳥和雌鳥，我們可能想知道頭長和體重之間的總體關系是否對每個性別分別成立。為了解決這個問題，我們可以按照鳥的性別對散點圖中的點進行著色（圖 12.2 ）。該圖顯示頭部長度和體重的總體趨勢，至少部分是由鳥類的性別驅動的。在相同的體重下，雌性的頭部往往比雄性短。與此同時，雌性平均比雄性輕。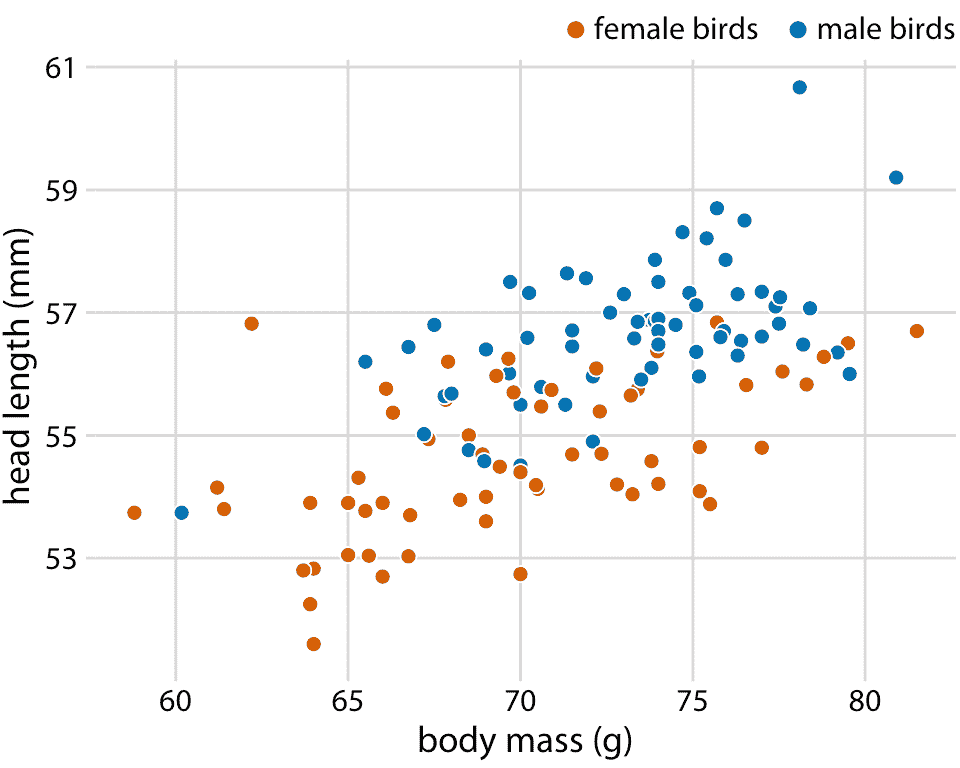  圖 12.2：123 只藍鳥的頭長與體重的關系。鳥的性別用顏色表示。在相同的體重下，雄鳥往往比雌鳥頭更長（特別是更長的喙部）。數據來源：歐柏林學院的 Keith Tarvin 因為頭部長度被定義為從喙尖到頭部后部的距離，所以較大的頭部長度可能意味著較長的喙，較大的頭骨或兩者。我們可以通過查看數據集中的另一個變量（頭骨大小）來理清喙部長度和頭骨大小，這與頭長相似但不包括喙部。由于我們已經將 *x* 位置用于體重，*y* 位置用于頭部長度 和點的顏色用于鳥類性別，我們需要另一種美學來繪制頭骨大小。一種選擇是使用點的大小，產生稱為氣泡圖的可視化（圖 12.3）。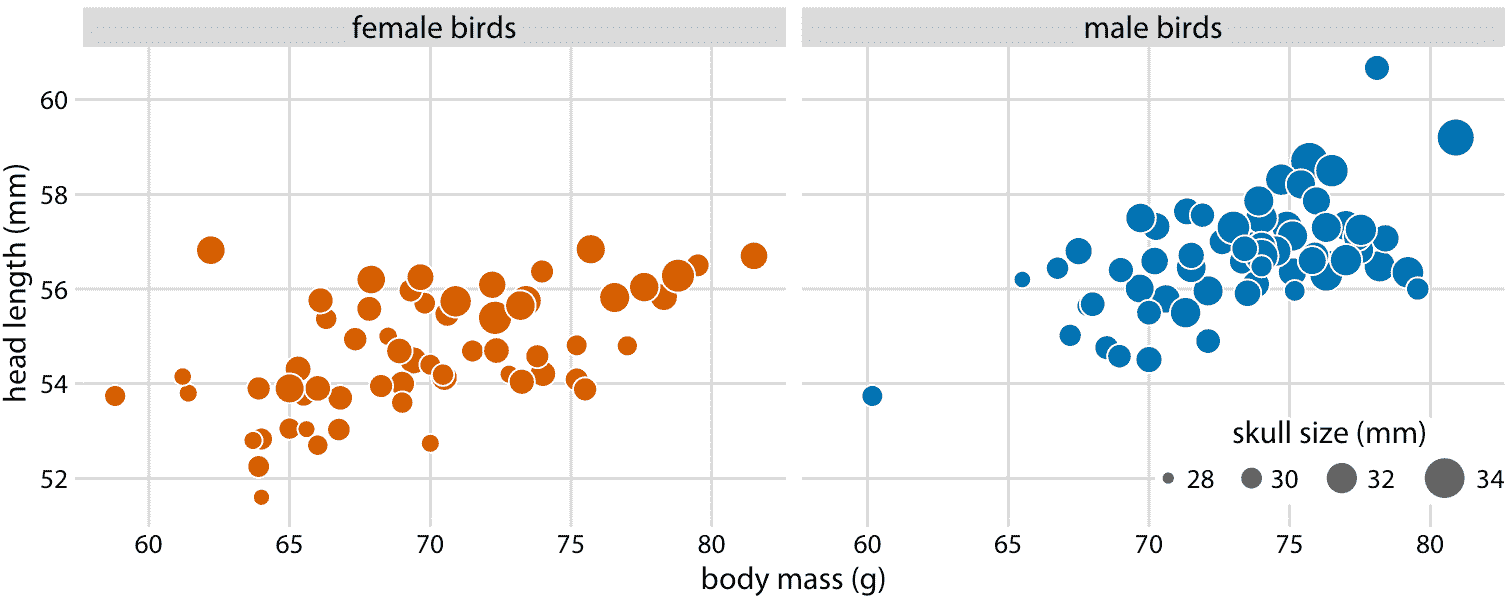  圖 12.3：123 只藍鳥的頭長與體重的關系。鳥的性別用顏色表示，鳥的頭骨大小用標記大小表示。頭部長度測量值包括喙部的長度，而頭骨大小測量值則不包括。頭部長度和頭骨大小往往是相關的，但是有些鳥類的頭骨大小非常長或短。數據來源：歐柏林學院的 Keith Tarvin 氣泡圖的缺點是它們顯示相同類型的變量，定量變量，具有兩種不同類型的比例，位置和大小。這使得難以在視覺上確定各種變量之間的關聯強度。此外，編碼為氣泡大小的數據值之間的差異，比編碼為位置的數據值之間的差異更難以察覺。因為即使最大的氣泡與總的圖形尺寸相比也需要稍微小一些，即使最大和最小氣泡之間的尺寸差異也必然很小。因此，數據值的較小差異將對應于實際上不可能看到的非常小的尺寸差異。在圖 12.3 中，我使用了一個尺寸映射，可以直觀地放大最小的頭骨（大約 28mm）和最大的頭骨（大約 34mm）之間的差異，但很難確定頭骨大小和體重或頭部長度之間的關系。 作為氣泡圖的替代方案，最好顯示一個根據全部變量的散點圖矩陣，其中每個單獨的圖顯示兩個數據維度（圖 12.4 ）。該圖清楚地表明，除了雌鳥往往稍微小一些之外，雌性和雄性鳥的頭骨大小和體重之間的關系是相似的。然而，頭部長度和體重之間的關系也是如此。不同性別有著顯著的差異。雄性鳥類的喙部通常比雌性鳥類更長，其他變量相同。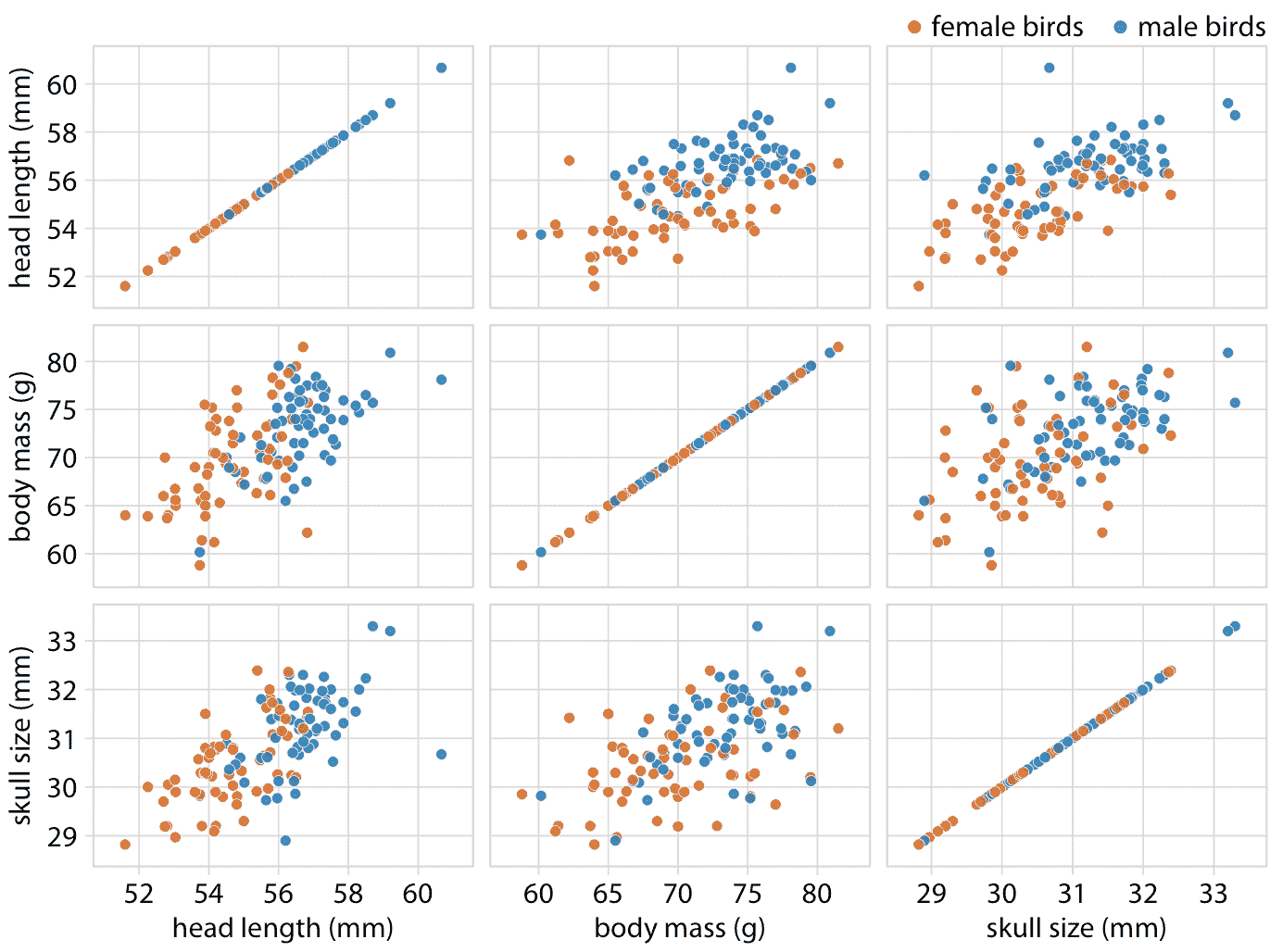  圖 12.4：123 只藍鳥的頭部長度，體重和頭骨大小的散點圖矩陣。該圖顯示了與圖 12.2 完全相同的數據。然而，因為我們更善于判斷位置而不是標記大小，所以在成對散點圖中，頭骨大小和其他兩個變量之間的相關性比圖 12.2 更容易察覺。數據來源：歐柏林學院的 Keith Tarvin ## 12.2 相關圖 當我們有超過三到四個量化變量時，散點圖矩陣很快變得難以處理。在這種情況下，量化變量對之間的關??聯量并使該數量可視化而不是原始數據更有用。一種常見的方法是計算相關系數。相關系數 *r* 是介于 -1 和 1 之間的數字，用于衡量兩個變量的變化程度。 *r = 0* 的值意味著沒有任何關聯，并且值 1 或 -1 表示完美關聯。相關系數的符號表示變量是正相關（一個變量中的較大值與另一個變量中的較大值一致）或負相關（一個變量中的較大值與另一個中的較小值一致）。為了提供不同相關強度的可視化示例，在圖 12.5 中，我顯示了隨機生成的點集，這些點在 *x* 和 *y* 的相關程度上有很大差異。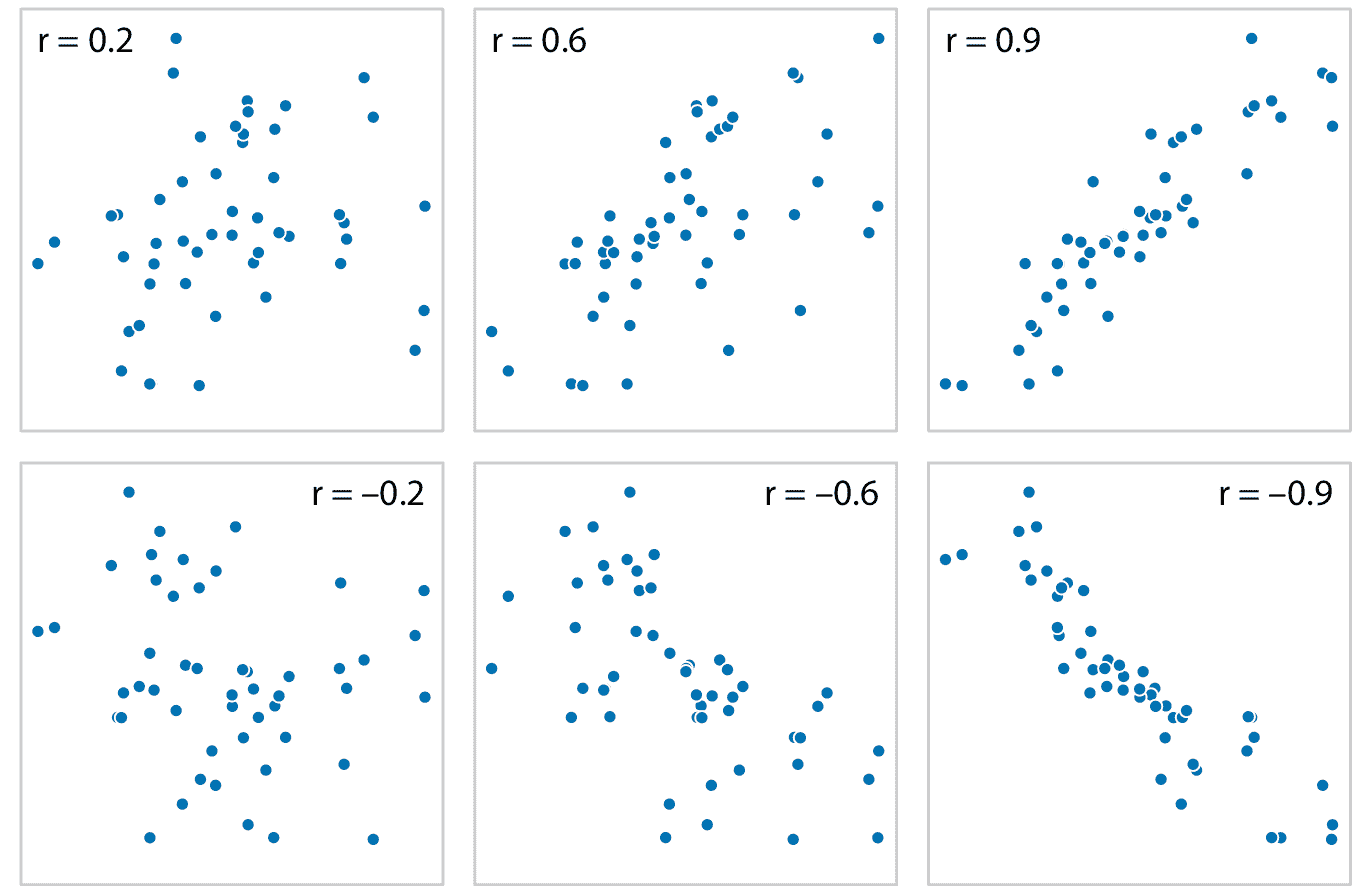  圖 12.5：不同幅度和方向的相關性示例，以及相關的相關系數 *r* 。在這兩行中，從左到右的相關性從弱到強。在頂行中，相關性為正（一個量的較大值與另一個量的較大值相關聯），在底行中它們為負（一個量的較大值與另一個量的較小值相關聯）。在所有六個圖中， *x* 和 *y* 值的集合是相同的，但是個體 *x* 和 *y* 值之間的配對已經重組來產生指定的相關系數。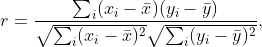 相關系數定義為  其中 $x_i$ 和 $y_i$ 是兩組觀測值，$\bar x$ 和 $\bar y$ 是相應的樣本均值。我們可以從這個公式中觀察到一些事情。首先，公式在 $x_i$ 和 $y_i$ 中是對稱的，因此 *x* 與 *y* 的相關性與 *y* 與 *x* 的相關性相同。其次，單個值 $x_i$ 和 $y_i$ 僅在相應樣本均值的差的上下文中輸入公式，因此如果我們以恒定的量移動整個數據集，例如對于某些常數 $C$，我們用 $x_i'= x_i + C$ 替換 $x_i$，相關系數保持不變。第三，如果我們重新調整數據，$x_i'= C x_i$，相關系數也保持不變，因為常數 $C$ 將出現在公式的分子和分母中，因此可以約分。 相關系數的可視化稱為相關圖。為了說明相關圖的使用，我們將考慮在取證工作期間獲得的 200 多個玻璃碎片的數據集。對于每個玻璃碎片，我們測量其成分，表示為各種礦物氧化物的重量百分比。我們測量了七種不同的氧化物，總共產生 6 + 5 + 4 + 3 + 2 + 1 = 21 對成對相關性。我們可以將這 21 個相關性一次顯示為彩色方塊矩陣，其中每個方塊代表一個相關系數（圖 12.6 ）。該相關圖允許我們快速掌握數據的趨勢，例如鎂與幾乎所有其他氧化物負相關，并且鋁和鋇具有強烈的正相關性。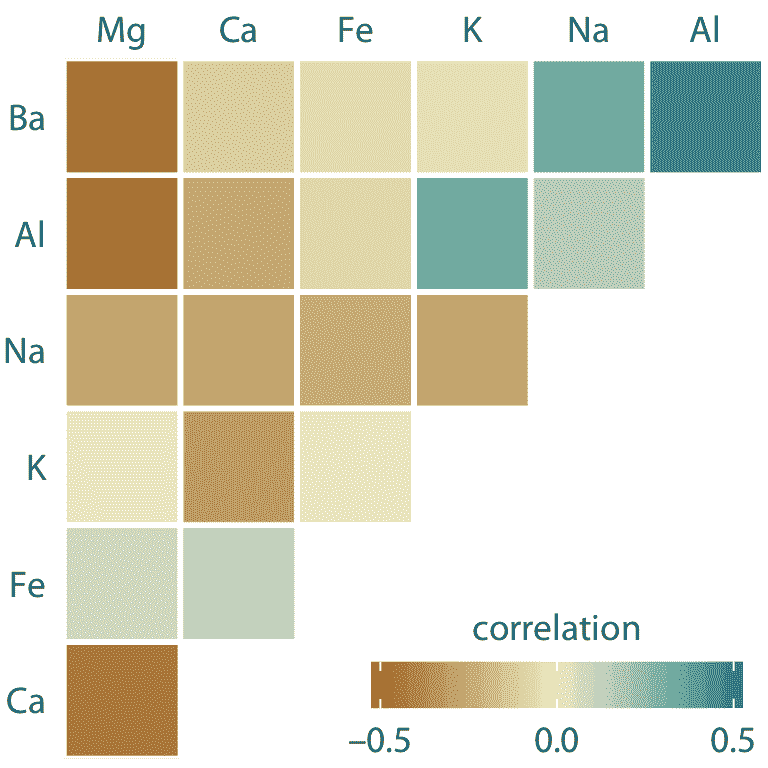  圖 12.6：取證工作期間獲得的 214 個玻璃碎片樣本的礦物質含量相關性。該數據集包含七個變量，用于測量每個玻璃片段中發現的鎂（Mg），鈣（Ca），鐵（Fe），鉀（K），鈉（Na），鋁（Al）和鋇（Ba）的含量。彩色方塊表示這些變量對之間的相關性。數據來源：B. German 圖 12.6 的相關圖的一個弱點是低相關性，即絕對值在零附近的相關性，不應該像這樣在視覺上被抑制。例如，鎂（Mg）和鉀（K）完全沒有相關性，但圖 12.6 沒有立即顯示出來。為了克服這個限制，我們可以將相關性顯示為彩色圓圈，并使用相關系數的絕對值來縮放圓形大小（圖 12.6 ）。以這種方式，低相關性被抑制并且高相關性更好地突出。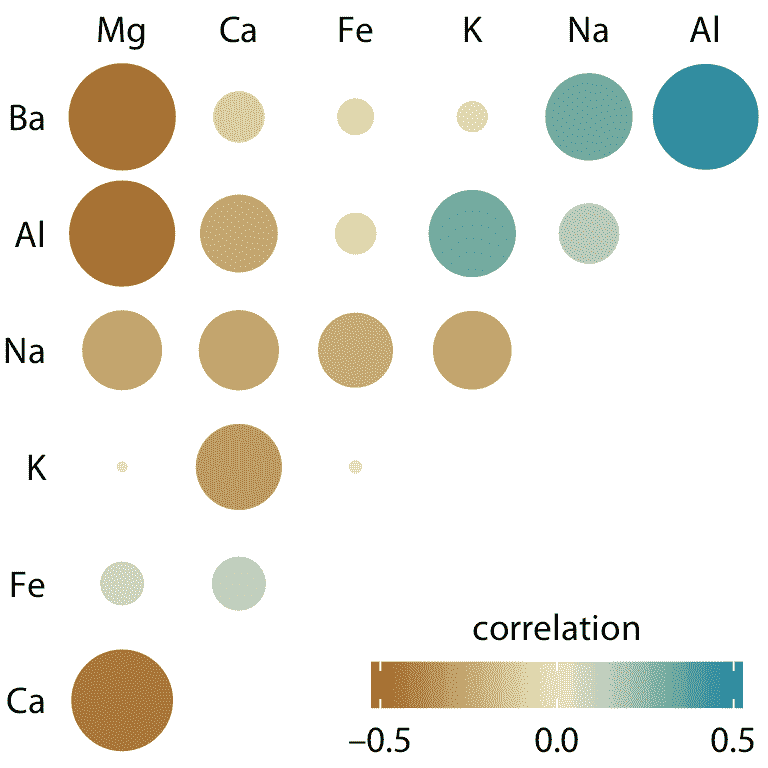  圖 12.7：取證玻璃樣本中礦物質含量的相關性。顏色刻度與圖 12.6 相同。但是，現在每個相關的幅度也以彩色圓圈的大小編碼。這種選擇在視覺上不強調相關性接近于零的情況。數據來源：B. German 所有相關圖都有一個重要的缺點：它們相當抽象。雖然它們向我們展示了數據中的重要模式，但它們也隱藏了基礎數據點，并可能使我們得出錯誤的結論。最好是可視化原始數據，而不是從中計算出的抽象的派生數量。幸運的是，我們經常可以在顯示重要模式和通過應用降維技術顯示原始數據之間找到一個平衡。 ## 12.3 降維 降維依賴于一個關鍵視角，即大多數高維數據集由多個相關變量組成，這些變量傳達重疊信息。這樣的數據集可以減少到較少數量的關鍵維度，而不會丟失太多關鍵信息。作為一個簡單直觀的例子，考慮一個人的多種身體特征的數據集，包括每個人的身高和體重，手臂和腿的長度，腰部，臀部和胸部的周長等數量。我們可以立即理解，所有這些數量將首先與每個人的總體規模相關。在其他條件相同的情況下，較大的人會更高，體重更重，手臂和腿更長，腰圍，臀部和胸圍更大。下一個重要的維度是人的性別。男性和女性的測量值對于大小相似的人來說是顯著不同的。例如，女人的臀圍往往比男人高，其他一切都是一致的。 有許多降維的技術。我將在這里討論一種最常用的技術，稱為主成分分析（PCA）。 PCA 通過數據中原始變量的線性組合引入一組新的變量（稱為主成分，PC），原始變量標準化為零均值和單位方差（參見圖 12.8 ，用于二維玩具示例） 。選擇主成分使得它們不相關，并且對它們進行排序，使得第一個成分捕獲數據中盡可能大的變化量，并且隨后的成分捕獲越來越少的變化量。通常，只能從前兩或三個主成分中看到數據中的關鍵特征。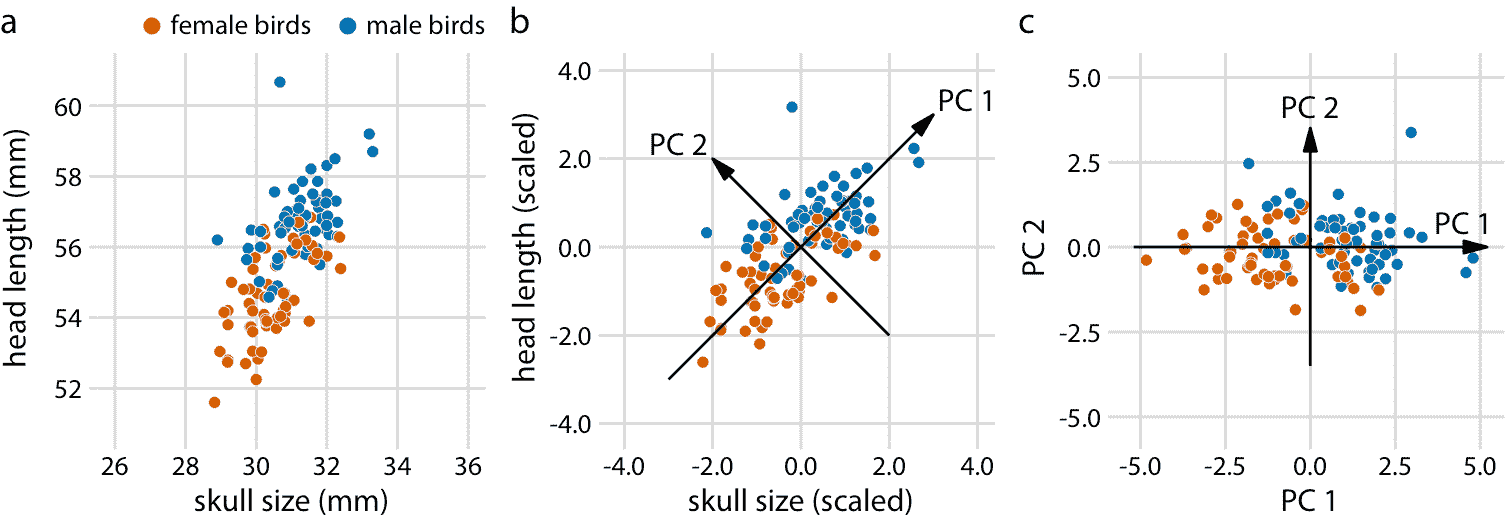  圖 12.8：二維示例主成分（PC）分析。 （a）原始數據。作為示例數據，我使用藍鳥數據集中的頭長和頭骨大小測量值。雌鳥和雄鳥以顏色區分，但這種區分對主成分分析沒有影響。 （b）作為 PCA 的第一步，我們將原始數據值縮放為零均值和單位方差。然后，我們沿著數據的最大變化方向定義新變量（主成分，PC）。 （c）最后，我們將數據投影到新坐標中。在數學上，該投影相當于數據點在原點周圍的旋轉。在此處顯示的 2D 示例中，數據點順時針旋轉 45 度。 當我們執行 PCA 時，我們通常對兩條信息感興趣：（i）主成分的組成和（ii）主成分空間中各個數據點的位置。讓我們在取證玻璃數據集的主成分分析中看一下這兩部分。 首先，我們來看主成分組成（圖 12.9）。在這里，我們只考慮前兩個成分，PC1 和 PC2。因為 PC 是原始變量（在標準化之后）的線性組合，我們可以將原始變量表示為箭頭，指示它們對主成分的貢獻程度。在這里，我們看到鋇和鈉主要貢獻于 PC1 而不是 PC2，鈣和鉀主要貢獻于 PC2 而不是 PC1，其他變量對兩種成分的貢獻不同（圖 12.9）。箭頭的長度各不相同，因為有兩個以上的主成分。例如，鐵的箭頭特別短，因為它主要用于高階主成分（未示出）。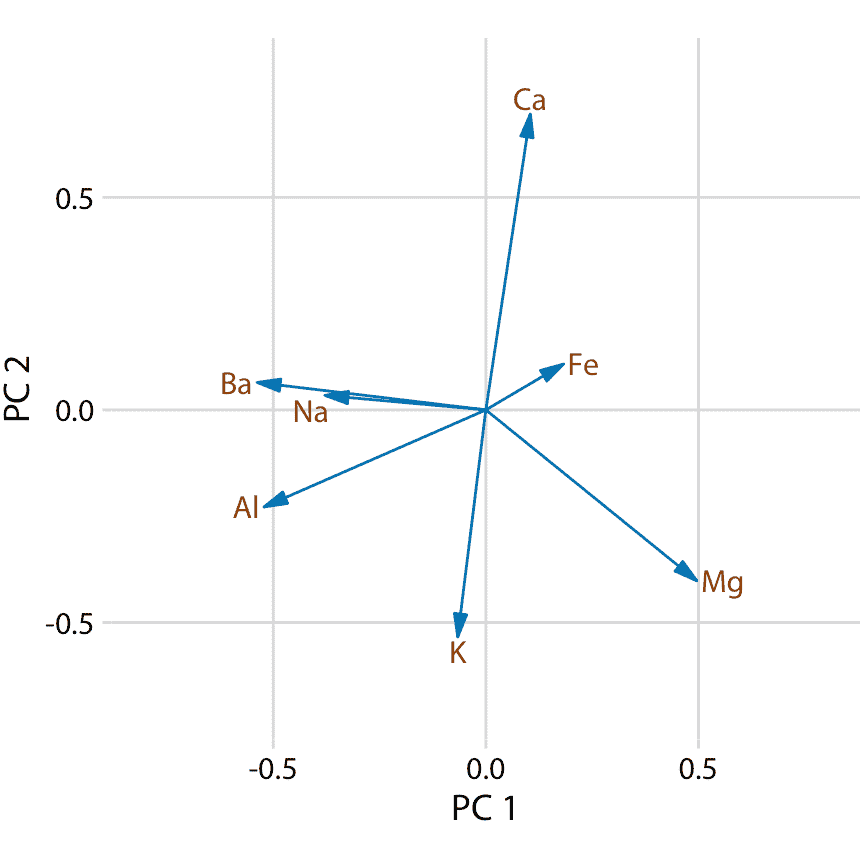  圖 12.9：取證玻璃數據集的主成分分析（PCA）中前兩個成分的組成。主成分 1（PC 1）主要測量玻璃碎片中鋁，鋇，鈉和鎂含量，而主成分 2（PC 2）主要測量鈣和鉀含量，并在一定程度上測量鋁和鎂的含量。 接下來，我們將原始數據投影到主成分空間（圖 12.10 ）。我們在該圖中看到了不同類型的玻璃碎片的清晰聚類。來自前照燈和車窗的碎片落入 PC 圖中清晰描繪的幾個區域，幾乎沒有離群點。來自餐具和容器的碎片更加分散，但與前照燈和窗戶碎片明顯不同。通過比較圖 12.10 和圖 12.9 ，我們可以得出結論，窗戶樣本的鎂含量高于平均值，鋇，鋁和鈉含量低于平均值，而前照燈樣本相反。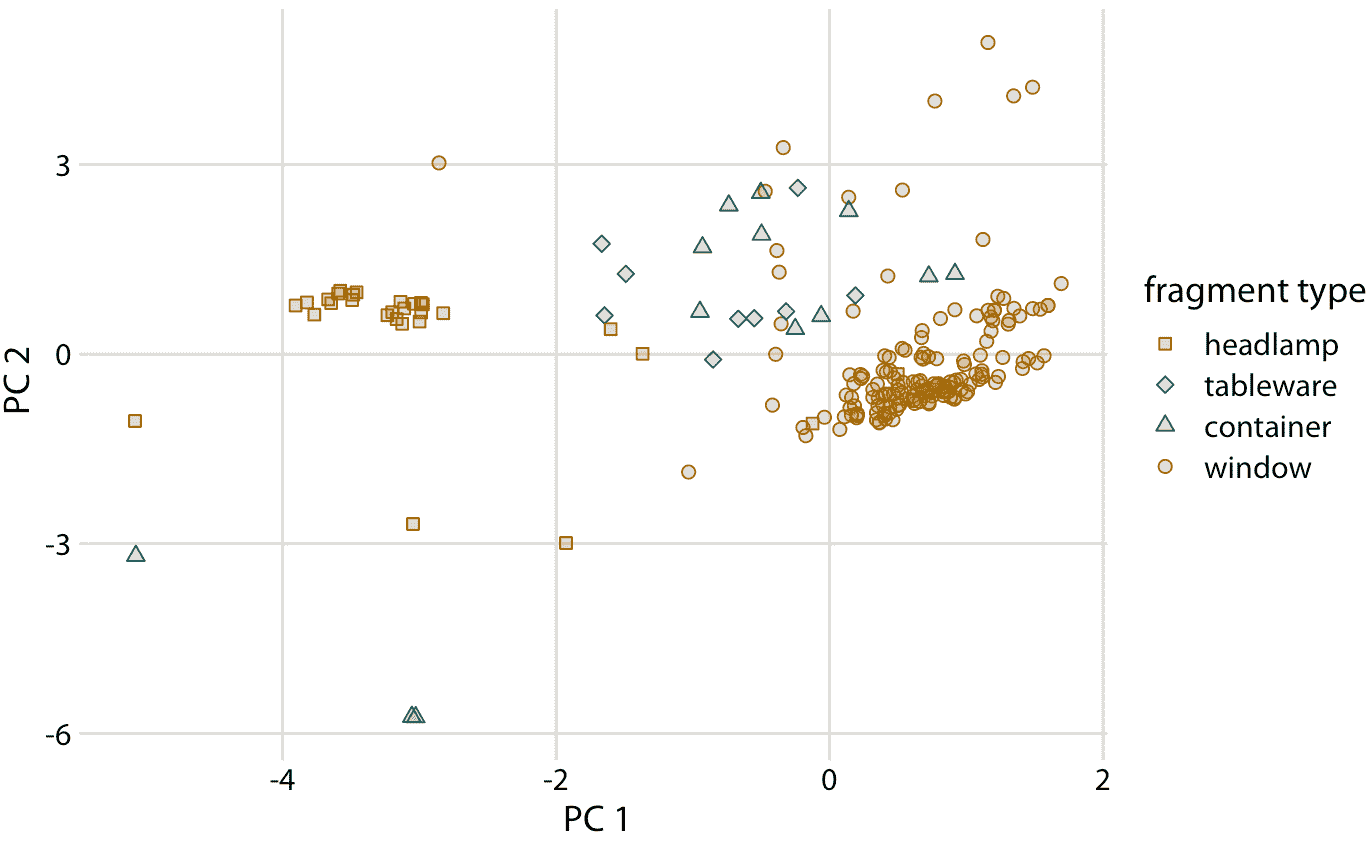  圖 12.10：單個玻璃碎片的組成，在 12.9 中定義的主成分空間中可視化。我們看到不同類型的玻璃樣本聚集在不同 PC1 和 2 的特征值上。特別是，前照燈的特征是負 PC1 值，而窗戶傾向于具有正 PC1 值。餐具和容器的 PC1 值接近零，并且往往具有正 PC2 值。但是，有一些例外情況，容器碎片同時具有負 PC1 值和負 PC2 值。這些碎片的組成與所分析的所有其他碎片完全不同。 ## 12.4 配對數據 多變量定量數據的一個特例是配對數據：在略微不同的條件下，有兩個或多個相同數量的測量值的數據。示例包括每個受試者的兩個類似測量值（例如，人的右臂和左臂的長度），在不同時間點對同一受試者的重復測量值（例如，一年中兩個不同時間的人的體重），或兩個密切相關的主題的測量值（例如，兩個同卵雙胞胎的高度）。對于配對數據，可以合理地假設，屬于一對的兩個測量值，而不是其他對的測量值彼此更相似。兩個雙胞胎的高度大約相同，但高度與其他雙胞胎不同。因此，對于配對數據，我們需要選擇可突出配對測量之間任何差異的可視化。 在這種情況下，一個很好的選擇是在對角線上標記 *x = y* 的簡單散點圖。在這樣的圖中，如果每對的兩個測量值之間的唯一差異是隨機噪聲，那么樣本中的所有點將圍繞該線對稱地分布。相比之下，配對測量值之間的任何系統差異，將在數據點相對于對角線向上或向下的系統移位中可見。例如，考慮一下 1970 年和 2010 年 166 個國家的人均二氧化碳（CO2）排放量（圖 12.11 ）。此示例突出顯示配對數據的兩個常見特征。首先，大多數點相對接近對角線。盡管各國的 CO2 排放量差異超過近四個數量級，但在 40 年的時間跨度內，每個國家的排放量相當一致。其次，這些點相對于對角線系統地向上移動。在所考慮的 40 年中，大多數國家的 CO2 排放量增加。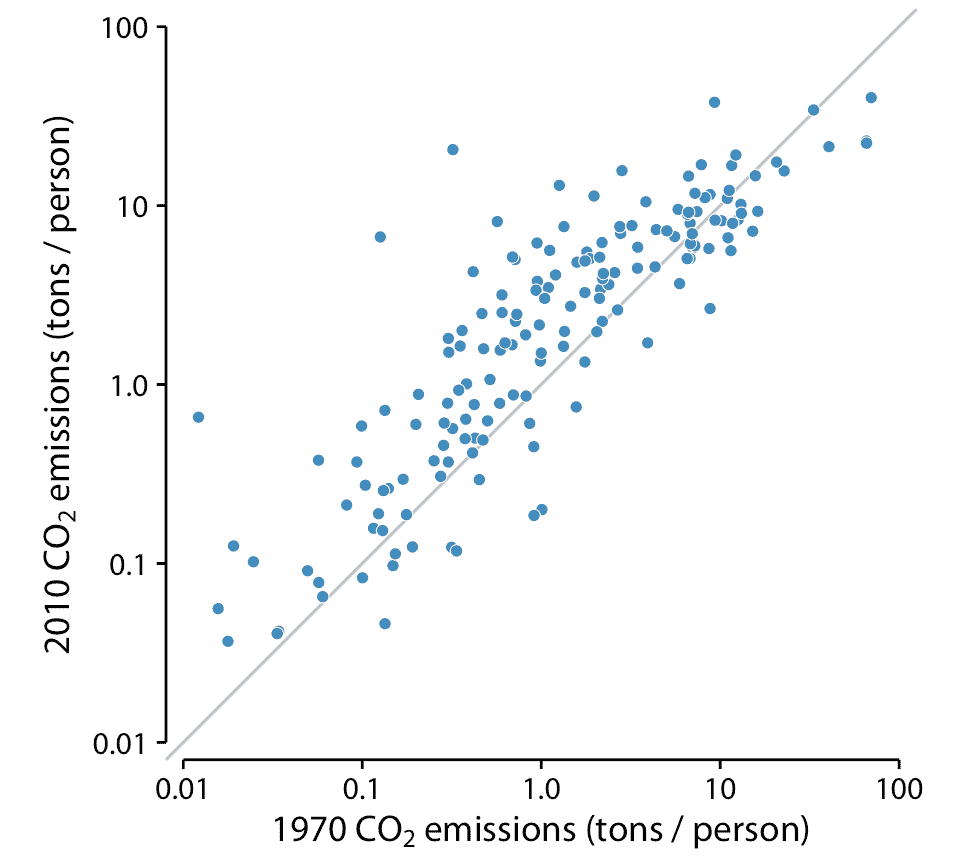  圖 12.11：1970 年和 2010 年，166 個國家的人均二氧化碳（CO2）排放量。每個點代表一個國家。對角線表示 1970 年和 2010 年的相同 CO2 排放量。這些點相對于對角線系統地向上移動：在大多數國家，2010 年的排放量高于 1970 年。數據來源：二氧化碳信息分析中心 當我們有大量數據點，和/或對整個數據集與零期望的系統偏差感興趣時，圖 12.11 這樣的散點圖很有效。相比之下，如果我們只有少量的觀測值，并且主要對每個個例的身份感興趣，那么斜率圖可能是更好的選擇。在斜率圖中，我們將各個測量值繪制為排列成兩列的點，并通過將成對的點與線連接來表示偶對。每條線的斜率突出了變化的幅度和方向。圖 12.12 使用這種方法顯示 2000 年至 2010 年間人均 CO2 排放量差異最大的 10 個國家。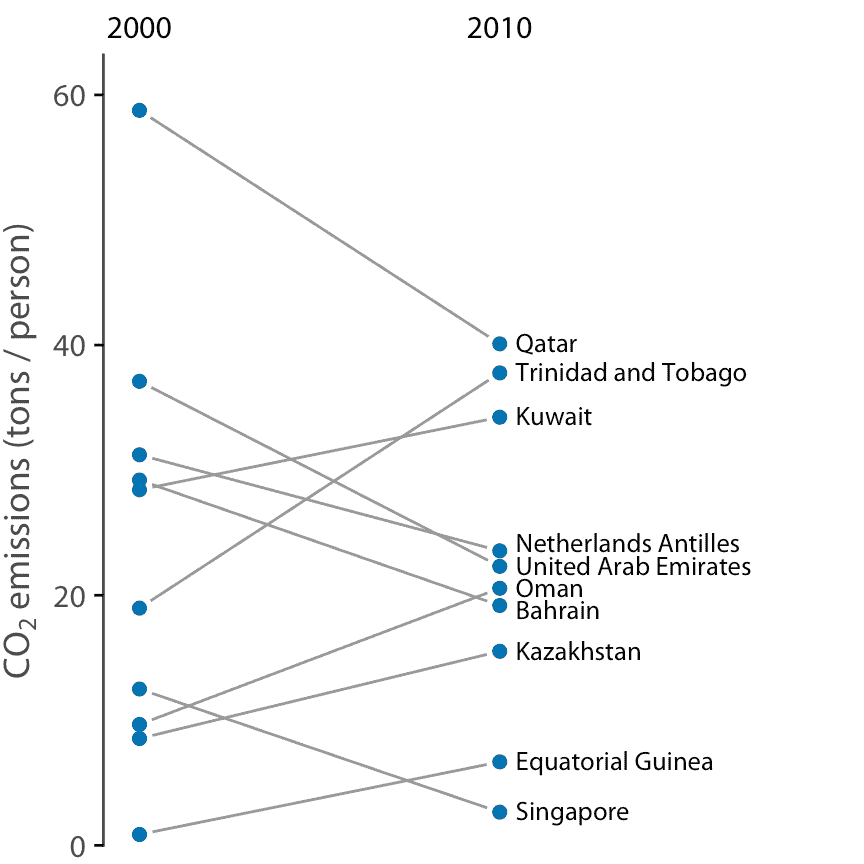  圖 12.12：2000 年和 2010 年人均二氧化碳（CO2）排放量，顯示差異最大的十個國家。數據來源：二氧化碳信息分析中心 與散點圖相比，斜率圖具有一個重要優勢：它們可用于一次比較兩個以上的測量值。例如，我們可以修改圖 12.12 來顯示三個時間點的 CO2 排放量，這里是 2000 年，2005 年和 2010 年（圖 12.13 ）。這一選擇突出了整個十年排放量發生重大變化的國家，以及卡塔爾或特立尼達和多巴哥等國家，它們的第一個和第二個五年間隔的趨勢有很大差異。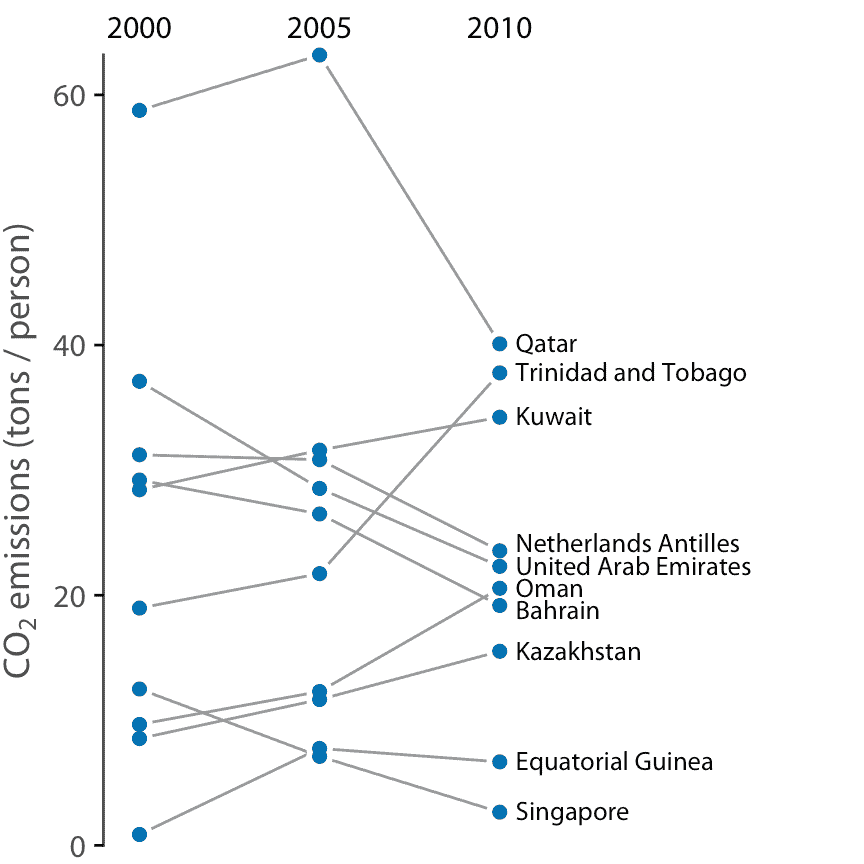  圖 12.13：2000 年，2005 年和 2010 年人均 CO2 排放量，顯示差異最大的 10 個國家。數據來源：二氧化碳信息分析中心