# 17 比例墨水原理 > 原文： [17 The principle of proportional ink](https://serialmentor.com/dataviz/proportional-ink.html) > 校驗：[飛龍](https://github.com/wizardforcel) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 在許多不同的可視化場景中，我們通過圖形元素的區域來表示數據值。例如，在條形圖中，我們繪制的條形圖從 0 開始并以它們代表的數據值結束。在這種情況下，數據值不僅編碼為條形的終點，而且編碼為條形的高度或長度。如果我們繪制一個以非 0 值開始的條形圖，則條形終點和條形長度將傳達矛盾的信息。這些數字在內部不一致，因為它們使用相同圖形元素顯示的兩個不同值。將此與我們使用點來可視化數據值的情況進行對比。在這種情況下，該值僅編碼為點的位置，而不是點的大小或形狀。 每當我們使用圖形元素（如條形，矩形，任意形狀的陰影區域）或任何其他具有明顯可視區域的元素時，都會出現類似的問題，這些元素可能與所顯示的數據值一致或不一致。在所有這些情況下，我們需要確保沒有不一致。這個概念被 Bergstrom 和 West 稱為比例墨水原理（Bergstrom 和 West [2016](#ref-BergstromWest2016) ）： > **比例墨水原理**：可視化中的陰影區域大小需要與它們所代表的數據值成比例。 （通常的做法是使用“墨水”一詞來指代偏離背景顏色的可視化的任何部分。這包括線條，點，陰影區域和文本。然而，在本章中，我們主要討論的是陰影區域。）違反這一原則的情況非常普遍，特別是在大眾媒體和金融界。 ## 17.1 沿線性軸可視化 我們首先考慮最常見的情景，即沿線性比例的數量可視化。圖 17.1 顯示夏威夷州的五個縣的收入中位數。這是報紙文章中可能遇到的典型圖像。快速瀏覽一下這個圖形表明，夏威夷縣非常貧窮，而檀香山縣比其他縣富裕得多。然而，圖 17.1 相當具有誤導性，因為所有條形都以 50,000 美元的收入中位數開始。因此，雖然每個條形的終點正確代表了每個縣的實際收入中位數，但條形高度代表收入中位數超過 50,000 美元的程度，這是一個任意數字。并且人類感知是這樣的：條形高度是我們在觀察該圖時所感知的關鍵數量，而不是條形終點相對于 *y* 軸的位置。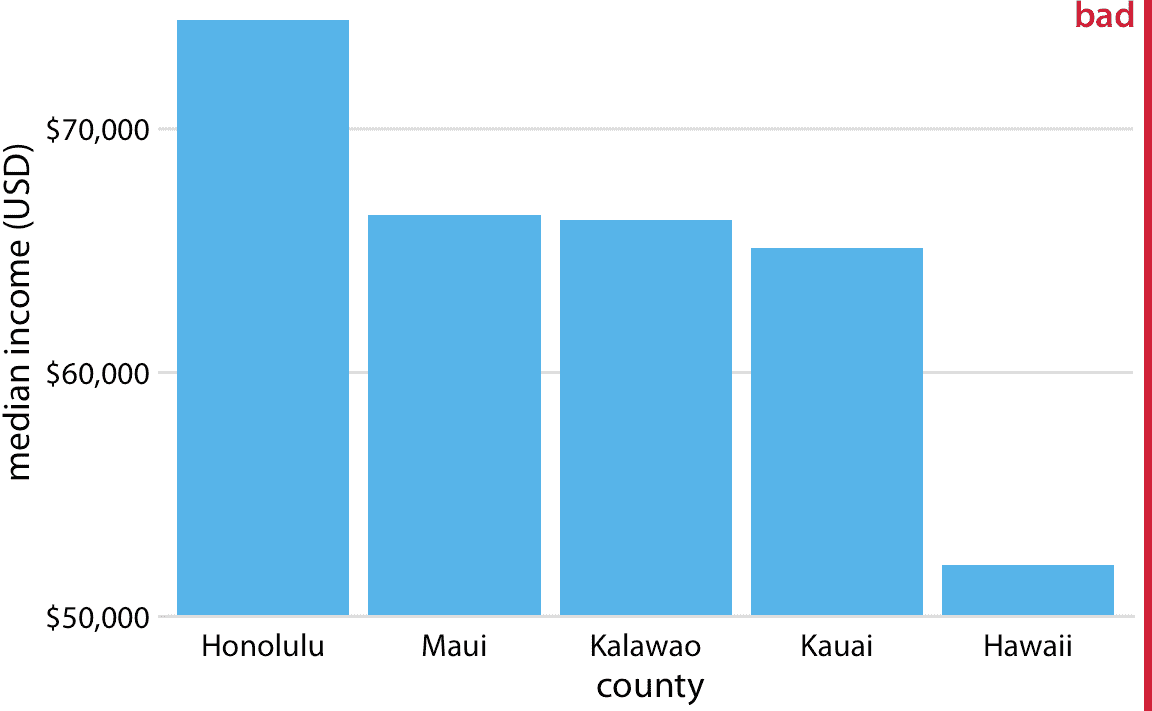  圖 17.1：夏威夷州五個縣的收入中位數。這個圖形具有誤導性，因為 *y* 軸刻度從 50,000 美元而不是 0 美元開始。結果，條形高度與所示數值不成比例，夏威夷縣與其他四個縣之間的收入差距看起來比實際大得多。數據來源：2015 年美國五年社區調查。 這些數據的適當可視化使得故事不那么令人激動（圖 17.2 ）。雖然各州之間的收入中位數存在差異，但它們遠遠沒有圖 17.1 所暗示的那么大。總體而言，不同縣的收入中位數是差不多的。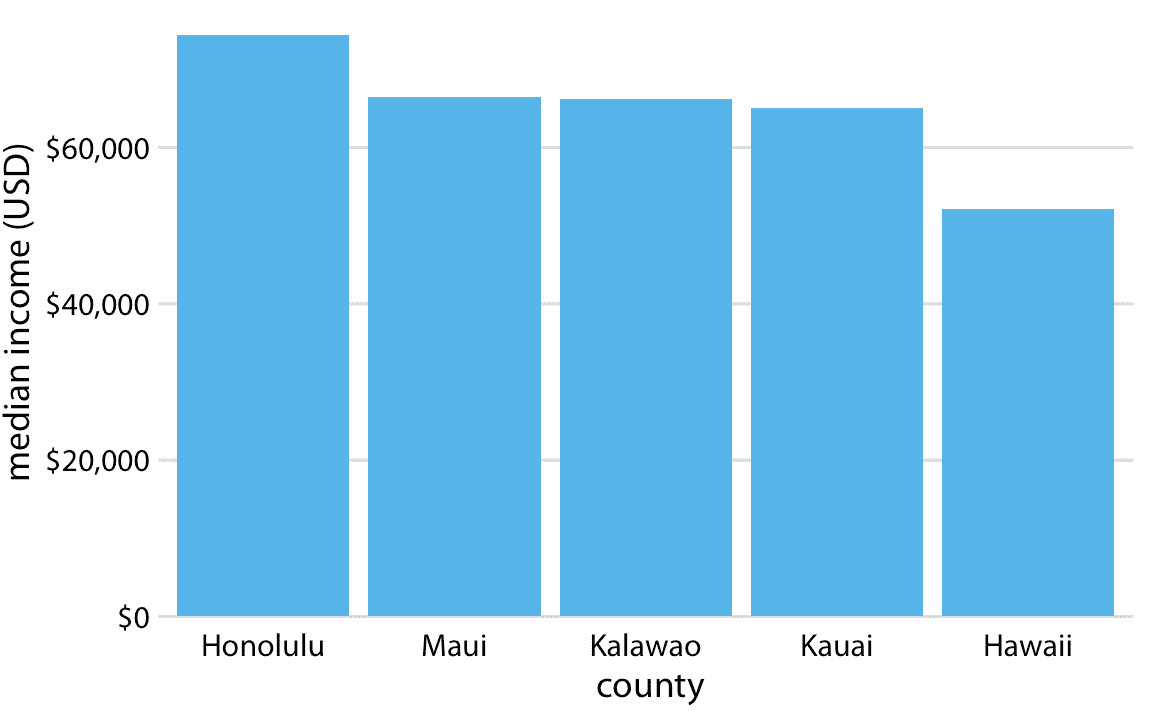  圖 17.2：夏威夷州五個縣的收入中位數。這里， *y* 軸刻度從 0 美元開始，因此準確顯示了五個縣的收入中位數的相對大小。數據來源：2015 年美國五年社區調查。 線性刻度上的條形應始終從 0 開始。 在時間序列的可視化中經常出現類似的可視化問題，例如股票價格的可視化問題。圖 17.3 表明 Facebook 股票價格在 2016 年 11 月 1 日左右大幅下跌。實際上，相對于股票總價格，價格下跌幅度較小（圖 17.4 ]）。即使沒有曲線下方的陰影，圖 17.3 中的 *y* 軸刻度也會有問題。但有了陰影，這個圖形變得特??別成問題。陰影強調從 *x* 軸的位置到所示的特定 *y* 值的距離，因此它產生視覺印象，即給定日期的陰影區域的高度代表那天的股票價格。相反，它只代表股票價格與基線的差異，圖 17.3 中為 110 美元。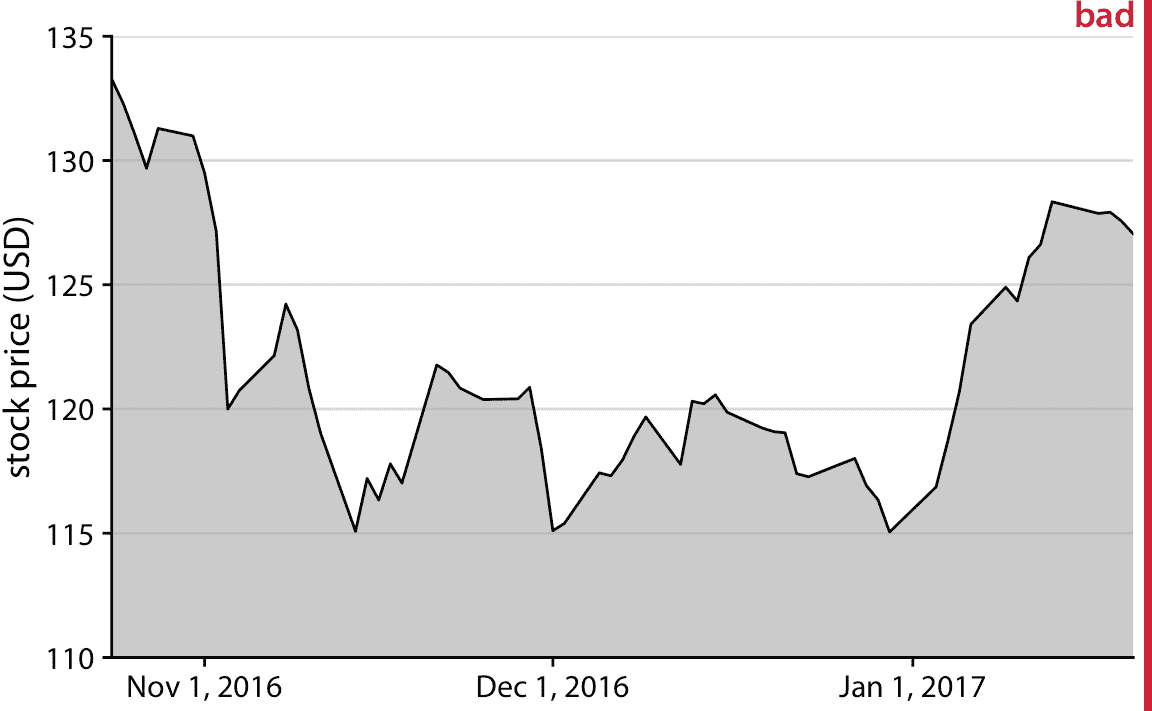  圖 17.3：2016 年 10 月 22 日到 2017 年 1 月 21 日的 Facebook（FB）的股票價格。這個圖形似乎意味著 Facebook 股票價格在 2016 年 11 月 1 日左右崩潰。但是，這是誤導性的，因為 *y* 軸的起價為 110 美元而不是 0 美元。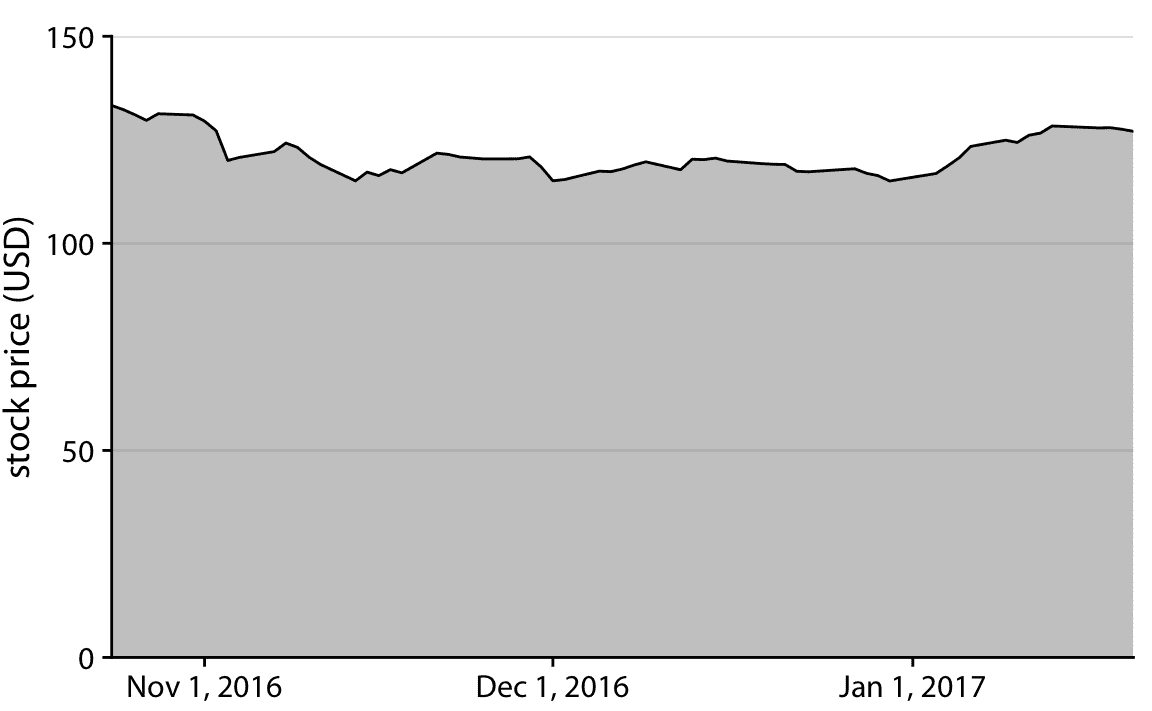  圖 17.4：2016 年 10 月 22 日至 2017 年 1 月 21 日的 Facebook（FB）的股票價格。通過在 0 美元到 150 美元的 *y* 軸上展示的股票價格，這個圖形更準確地傳遞了 2016 年 11 月 1 日左右的 FB 價格下跌的幅度。 圖 17.2 和圖 17.4 的例子可能表明，條形和陰影區域不能用于表示隨時間的微小變化，或條件之間的差異，因為我們總是需要畫出整個條形或從 0 開始的區域。但事實并非如此。使用條形或陰影區域來顯示條件之間的差異是完全有效的，只要我們明確說明我們顯示的差異。例如，我們可以使用條形圖來顯示 2010 年至 2015 年夏威夷縣收入中位數的變化（圖 17.5 ）。對于除卡拉沃以外的所有縣，這一變化不到 5000 美元。 （卡拉沃是一個不同尋常的縣，人口不到 100 人，少數人進出該縣可能產生收入中位數的大幅波動。）對于夏威夷縣，這種變化是負面的，即 2015 年的收入中位數低于 2010 年。我們通過繪制相反方向的條形來表示負值，即從 0 向下而不是向上延伸。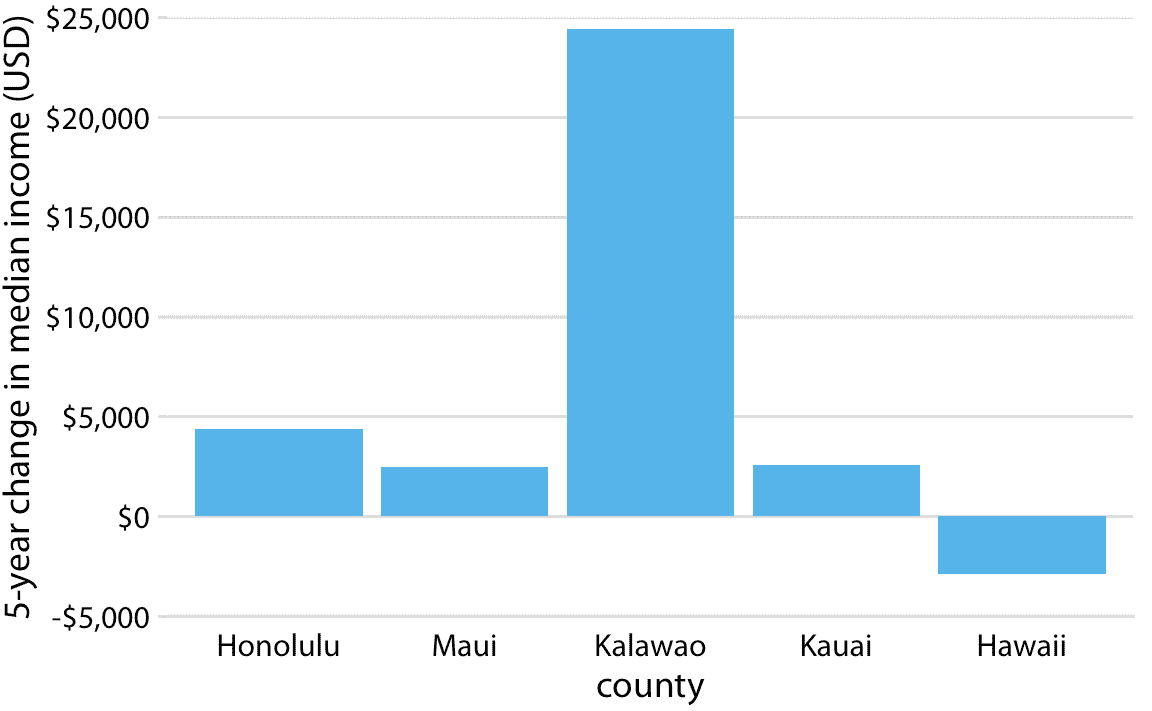  圖 17.5：2010 年至 2015 年夏威夷縣收入中位數的變化。數據來源：2010 年和 2015 年美國五年社區調查。 同樣，我們可以將 Facebook 隨時間變化的股票價格，繪制為與 2016 年 10 月 22 日的臨時峰值的差異（圖 17.6 ）。通過著色表示與峰值的距離的區域，我們可以準確地表示價格下降的絕對值，而不會對價格下降相對于總股價的幅度，做出任何隱含的陳述。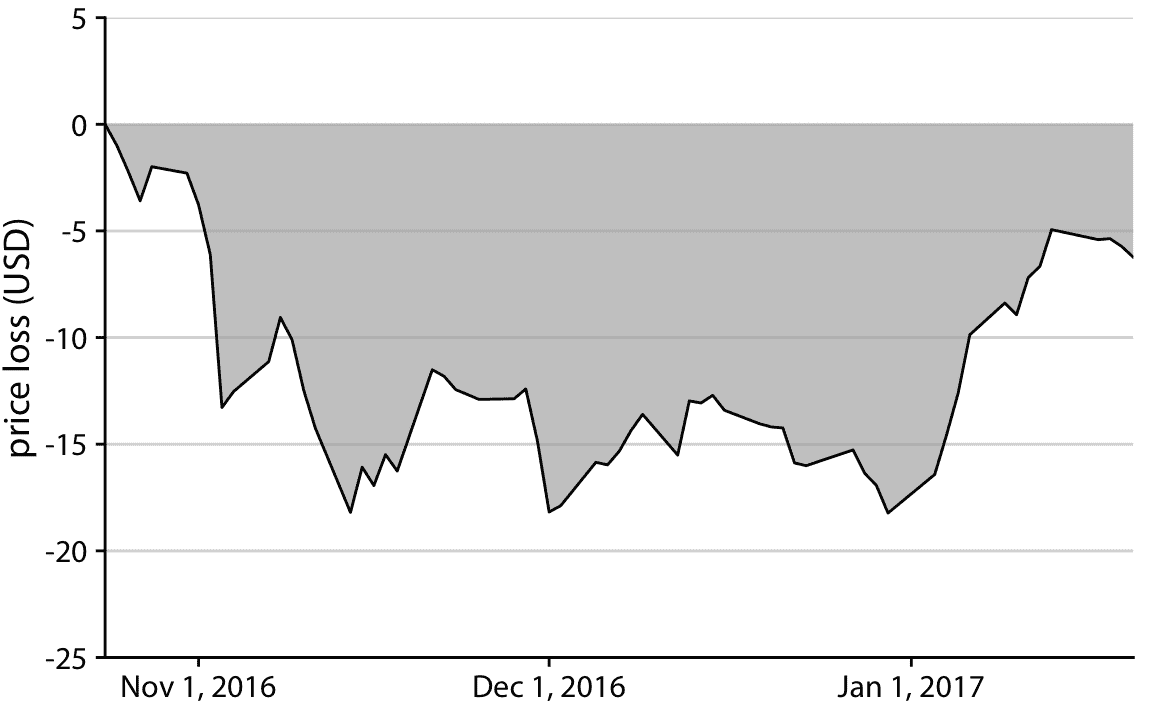  圖 17.6：Facebook（FB）股票價格相對于 2016 年 10 月 22 日價格的損失。2016 年 11 月 1 日至 2017 年 1 月 1 日期間，價格比 2016 年 10 月 22 日的峰值低了約 15 美元。但隨后價格在 2017 年 1 月開始復蘇。 ## 17.2 沿對數軸的可視化 當我們沿線性刻度可視化數據時，條形，矩形或其他形狀的區域自動與數據值成比例。如果我們使用對數刻度，則情況并非如此，因為數據值不是沿軸線性間隔的。因此，有人可能會爭論說，例如，對數刻度上的條形圖本質上存在缺陷。另一方面，每個條形的面積將與數據值的對數成比例，因此對數刻度上的條形圖滿足對數變換坐標中的比例墨水原理。在實踐中，我認為這兩個論點都不能解釋對數比例條形圖是否合適。相反，相關的問題是我們是否想要可視化數量或比率。 在第三章中，我已經解釋了對數刻度是可視化比率的自然刻度，因為沿對數刻度的單位步長對應于乘以或除以常數因子。然而，在實踐中，對數刻度通常并與專門用于可視化比率，而是因為顯示的數字在很多數量級上變化。例如，考慮大洋洲國家的 2007 年國內生產總值（GDP），這些數字從不到 10 億美元（USD）到超過 3000 億美元不等（圖 17.7）。以線性刻度可視化這些數字是行不通的，因為 GDP 最大的兩個國家（新西蘭和澳大利亞）將主導這一繪圖。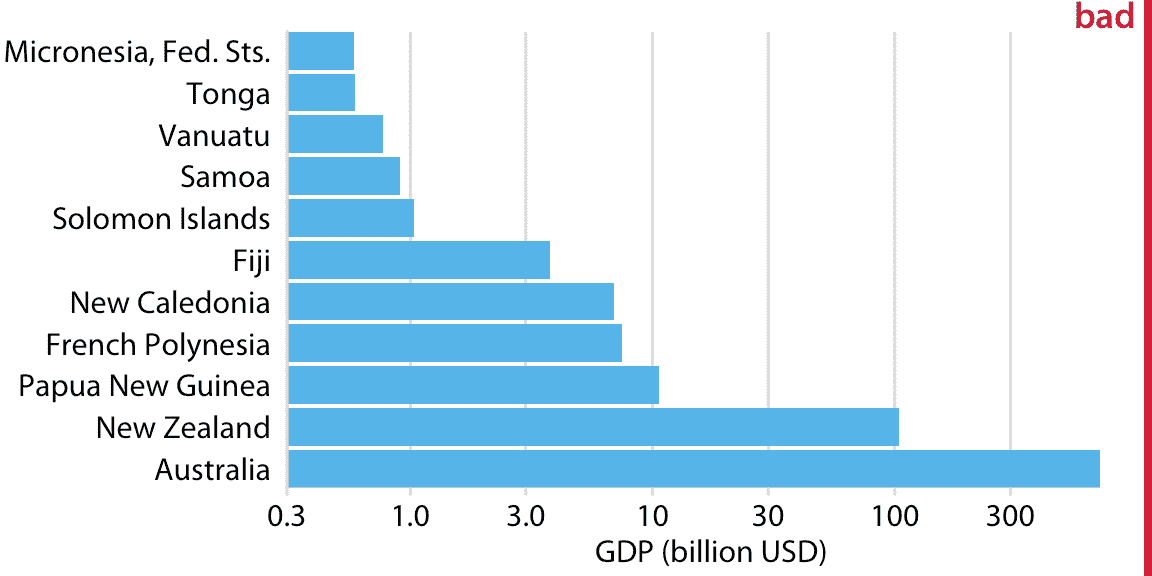  圖 17.7：2007 年大洋洲國家的國內生產總值。條形的長度不能準確反映所顯示的數據值，因為條形起始于 3 億美元的任意值。數據來源：Gapminder。 但是，對數刻度上使用條形的可視化（圖 17.7）也不起作用。條形起始于 3 億美元的任意值，并且至少該繪圖受到圖 17.1 的相同問題的影響，條形長度不代表數據值。然而，對數刻度的額外難度在于我們不能簡單地讓條形從 0 開始。在圖 17.7 中，值 0 將位于左側無限遠。因此，我們可以通過把它們的原點推得更遠，來使我們的條形任意長，參見例如圖 17.8 。當我們嘗試在對數刻度上可視化數量（這是 GDP 值）時，總會出現這個問題。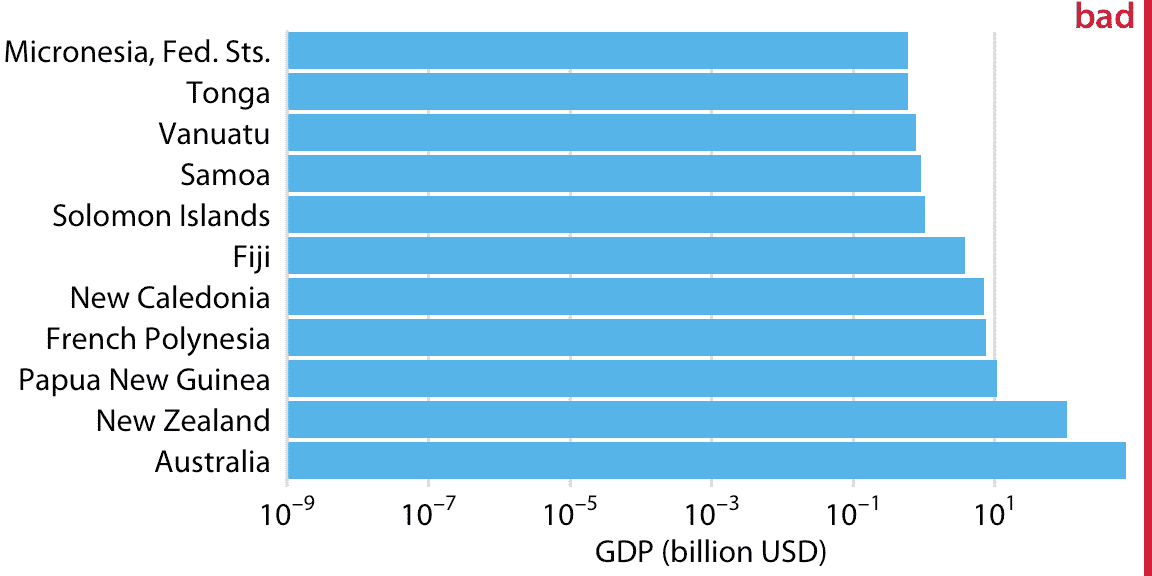  圖 17.8：2007 年大洋洲國家的國內生產總值。條形的長度不能準確反映所示的數據值，因為條形起始于任意值 10^(-9) 十億美元。數據來源：Gapminder。 對于圖 17.7 的數據，我認為條形圖是不合適的。相反，我們可以簡單地沿著刻度，為每個國家的 GDP 在適當位置放置一個點，并完全避免條形長度問題（圖 17.9 ）。重要的是，通過將國家名稱放在點的旁邊而不是沿著 *y* 軸，我們避免產生幅度的視覺感知，由國家名稱到點的距離所傳達。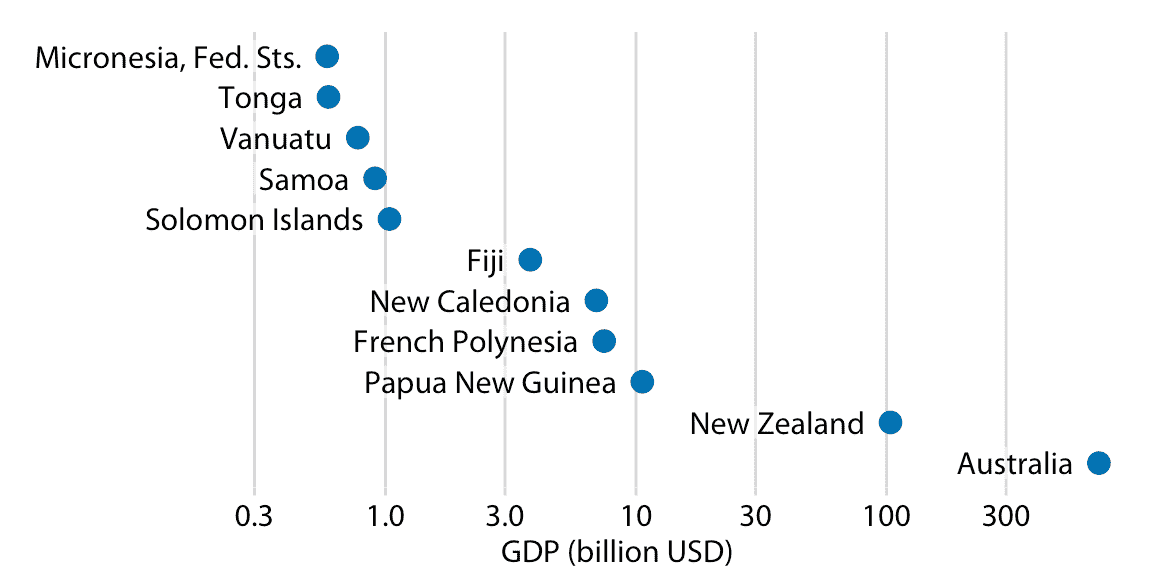  圖 17.9：2007 年大洋洲國家的國內生產總值。數據來源：Gapminder。 但是，如果我們想要顯示比率而不是數量，那么對數刻度上的條形是一個非常好的選擇。實際上，在這種情況下，它們優于線性刻度上的條形。例如，讓我們想象一下大洋洲國家的 GDP 值，相對于巴布亞新幾內亞的 GDP。由此產生的繪圖很好地突出了各國 GDP 之間的關鍵關系（圖 17.10 ）。我們可以看到，新西蘭的 GDP 超過巴布亞新幾內亞的八倍，澳大利亞的 GDP 超過 64 倍，而湯加和密克羅尼西亞聯邦的 GDP 不到巴布亞新幾內亞國內生產總值的十六分之一。法屬波利尼西亞和新喀里多尼亞相近，但 GDP 略低于巴布亞新幾內亞。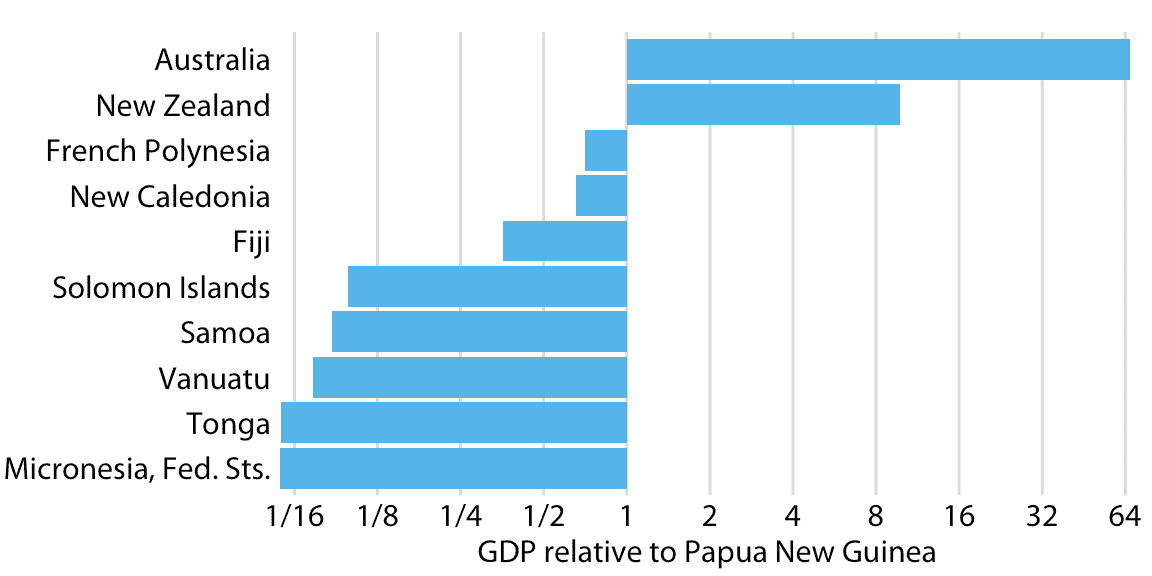  圖 17.10：2007 年大洋洲國家的國內生產總值，相對于巴布亞新幾內亞的國內生產總值。數據來源：Gapminder。 圖 17.10 還突出顯示對數刻度的自然中點為 1，表示大于 1 的數字的條形在一個方向上延伸，表示小于 1 的數字的條形在另一個方向上延伸條形。對數刻度上的條形表示比率，并且必須始終從 1 開始，線性刻度上的條形表示數量，并且必須始終從 0 開始。 在對數刻度上繪制條形時，它們表示比率，需要從 1 開始繪制，而不是 0。 ## 17.3 直接區域的可視化 所有前述示例沿一個線性維度可視化數據，使得數據值編碼為沿著 *x* 或 *y* 軸的面積和位置。在這些情況下，我們可以將數據值的面積編碼視為相對于位置編碼的偶然和次要編碼。然而，其他可視化方法主要或直接由面積表示數據值，而沒有相應的位置映射。最常見的是餅圖（圖 17.11 ）。盡管從技術上講，數據值被映射到角度，這些角度由沿著圓軸的位置表示，但實際上我們通常不會判斷餅圖的角度。相反，我們關注的主要視覺特性，是每個楔形區域的大小。  圖 17.11：羅德島縣的居民人數，以餅圖形示。每個楔形的角度和面積都與各個縣的居民數量成比例。數據來源：2010 年美國十年普查。 因為每個楔形的面積與其角度成比例，該角度與楔形所代表的數據值成比例，所以餅圖滿足比例墨水原理。但是，我們認為餅圖中的面積與條形圖中的相同面積不同。根本原因是人類感知主要判斷距離而不是面積。因此，如果數據值完全被編碼為距離，如條形長度的情況，比起數據值編碼為兩三個距離的組合，它們共同創建一個區域的情況，我們更準確地感知它。為了看到這種差異，比較圖 17.11 和圖 17.12 ，它使用條形顯示相同的數據。普羅維登斯縣和其他縣之間居民人數的差異在圖 17.12 中比在圖 17.11 中更大。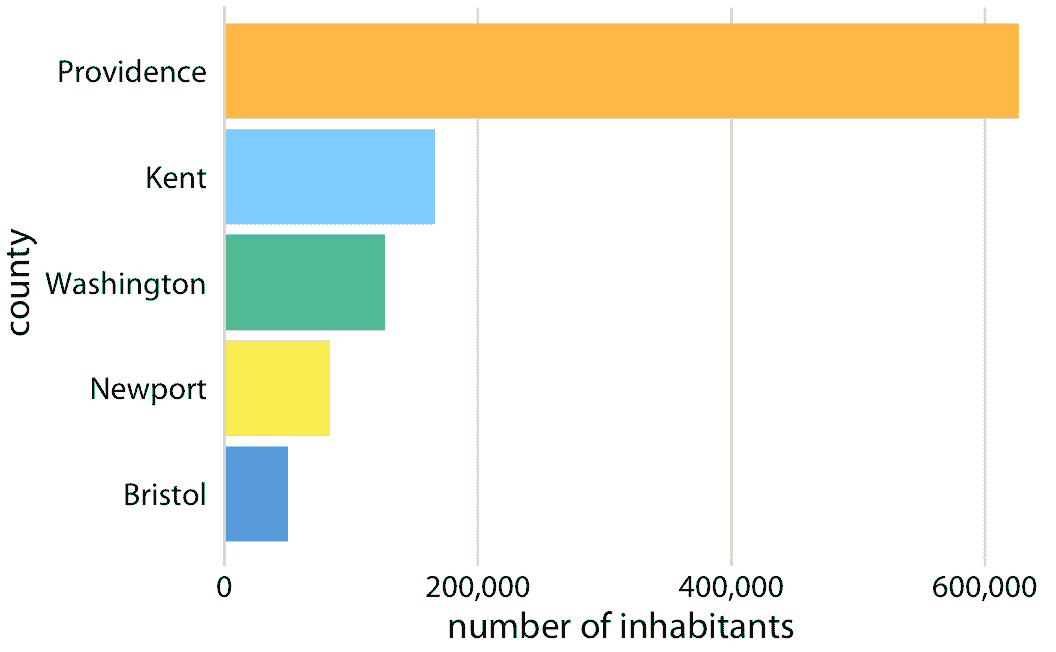  圖 17.12：羅德島縣的居民人數，以條形圖形示。每個條形的長度與各自縣的居民數量成比例。數據來源：2010 年美國十年普查。 人類感知更善于判斷距離而不是判斷區域的問題，也出現在樹形圖中（圖 17.13 ），可以將其視為餅圖的方形版本。同樣，與圖 17.12 相比，各縣居民數量的差異在圖 17.13 中顯得不太明顯。  圖 17.13：羅德島縣的居民人數，以樹形圖顯示。每個矩形的面積與相應縣的居民數量成比例。數據來源：2010 年美國十年普查。 ### 參考 ``` Bergstrom, C. T., and J. West. 2016. “The Principle of Proportional Ink.” http://callingbullshit.org/tools/tools_proportional_ink.html. ```