# 16 可視化不確定性 > 原文： [16 Visualizing uncertainty](https://serialmentor.com/dataviz/visualizing-uncertainty.html) > 校驗：[飛龍](https://github.com/wizardforcel) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 數據可視化最具挑戰性的方面之一是不確定性的可視化。當我們看到在特定位置繪制的數據點時，我們傾向于將其解釋為真實數據值的精確表示。很難想象數據點實際上可能位于尚未繪制的某個位置。然而，這種情況在數據可視化中無處不在。幾乎我們使用的每個數據集都有一些不確定性，我們選擇表示這種不確定性的方式，對我們的受眾多么準確地感知數據的含義，可能產生重大影響。 指示不確定性的兩種常用方法，是誤差條和置信帶。這些方法是在科學出版物的背景下開發的，它們需要正確解釋一些專業知識。然而，它們精確且節省空間。例如，通過使用誤差條，我們可以在單個圖中顯示許多不同參數估計值的不確定性。然而，對于非專業讀者而言，產生不確定性的強烈直觀印象的可視化策略可能更好，即使它們的代價是降低可視化精度或減少密集數據的展示。這里的選項包括頻率成幀，我們以近似比例明確繪制不同的可能場景，或者循環不同可能場景的動畫。 ## 16.1 將概率表現為頻率 在我們討論如何可視化不確定性之前，我們需要定義它實際上是什么。我們可以在未來事件的背景下直觀掌握不確定性的概念。如果我要翻硬幣，我不知道結果會是什么樣。最終的結果是不確定的。不過，我也不確定過去的事件。如果昨天我從我的廚房窗戶向外看了兩次，一次是在早上 8 點，一次是在下午 4 點，我在早上 8 點看到一輛紅色汽車停在街對面，下午 4 點沒有，然后我可以總結，汽車在八小時的時間窗口中的某個時間點離開了，但我不確切知道是什么時候。可能是上午 8:01，上午 9:30，下午 2 點，或者在這八個小時的任何其他時間。 在數學上，我們通過使用概率概念來處理不確定性。概率的精確定義很復雜，遠遠超出了本書的范圍。然而，我們可以在不了解數學的所有錯綜復雜的細節的情況下，成功地推導概率。對于許多實際相關的問題，考慮相對頻率就足夠了。假設您執行某種隨機試驗，例如擲硬幣或擲骰子，并尋找特定結果（例如，正面或六點）。你可以稱這個結果為成功，和任何其他結果為失敗。然后，如果你一遍又一遍地重復隨機試驗，成功的概率大約由你看到結果的一小部分給出。例如，如果特定結果以 10% 的概率發生，那么我們預計在許多重復試驗中，結果將在大約十分之一的情況中出現。 可視化單個概率很困難。你如何可視化在彩票中獲勝，或者用勻質的骰子擲出六點的幾率？在這兩種情況下，概率都是單個數字。我們可以將該數字視為一個數量，并使用第六章中討論的任何技術顯示它，例如條形圖或點圖，但結果不會非常有用。大多數人缺乏概率值如何轉化為經驗現實的直觀理解。將概率值顯示為條形或作為點放在一條線上，無助于此問題。 我們可以通過創建一個圖形，強調隨機試驗的頻率切面和不可預測性，來使概率概念變得有形，例如通過繪制隨機排列的不同顏色的方塊。在圖 16.1 中，我使用這種技術可視化三種不同的概率，1% 的成功幾率，10% 的成功幾率和 40% 的成功率。為了閱讀這個圖，想象一下，你得到了一個選擇深色方塊的任務，通過選擇一個方塊，然后看到哪個方塊是深色，哪個方塊是淺色。 （如果你愿意的話，你可以考慮閉著眼睛挑選一個方塊。）直觀地說，你可能會理解在 1% 幾率情況下，不太可能選擇一個深色的方塊。同樣，在 10% 幾率 的情況下，仍然不太可能選擇深色的方塊。然而，在 40% 的情況下，勝率看起來并不那么糟糕。這種可視化風格，其中我們顯示特定的潛在結果，被稱為離散結果可視化，并且將概率可視化為頻率的行為被稱為頻率成幀。我們根據易于理解的結果的頻率來表現結果的概率性質。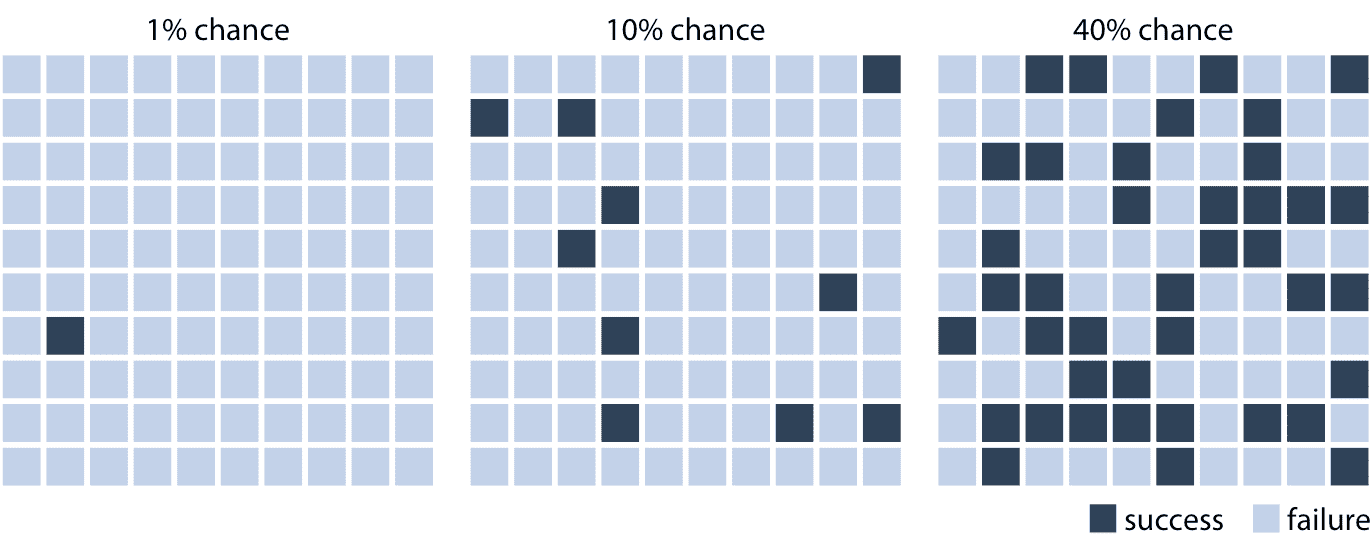  圖 16.1：將概率可視化為頻率。每個網格中有 100 個方塊，每個方塊表示在某些隨機試驗中成功或失敗。 1% 的成功幾率對應于一個深色和 99 個淺色方塊，10% 的成功幾率對應于十個深色和 90 個淺色方塊，并且 40% 的成功幾率對應于 40 個深色和 60 個淺色方塊。通過在淺色方塊中隨機放置深色方塊，我們可以創建隨機性的視覺印象，強調單個試驗結果的不確定性。 如果我們只對兩個不連續的結果（成功或失敗）感興趣，那么諸如圖 16.1 之類的可視化就可以正常工作。然而，我們經常處理更復雜的情況，其中隨機試驗的結果是數字變量。一個常見的情況是選舉預測，我們不僅對誰將獲勝而且對多少人感興趣。讓我們考慮一個假設的例子，即即將舉行的選舉，包括黃方和藍方。假設您在廣播中聽到藍方預計比黃方有一個百分點的優勢，誤差率為 1.76 個百分點。這些信息告訴你選舉的可能結果是什么？聽到“藍方會贏”是人類本性，但現實更為復雜。首先，最重要的是，有一系列不同的可能結果。藍方最終可能以 2 個百分點的領先優勢贏得選舉，或者黃方最終以半個百分點的領先優勢獲勝。可能結果的范圍及其相關可能性稱為概率分布，我們可以將其繪制為平滑曲線，該曲線上升然后落在可能結果的范圍內（圖 16.2 ）。特定結果的曲線越高，結果越可能。概率分布與第七章中討論的直方圖和核密度密切相關，您可能需要重新閱讀該章以刷新記憶。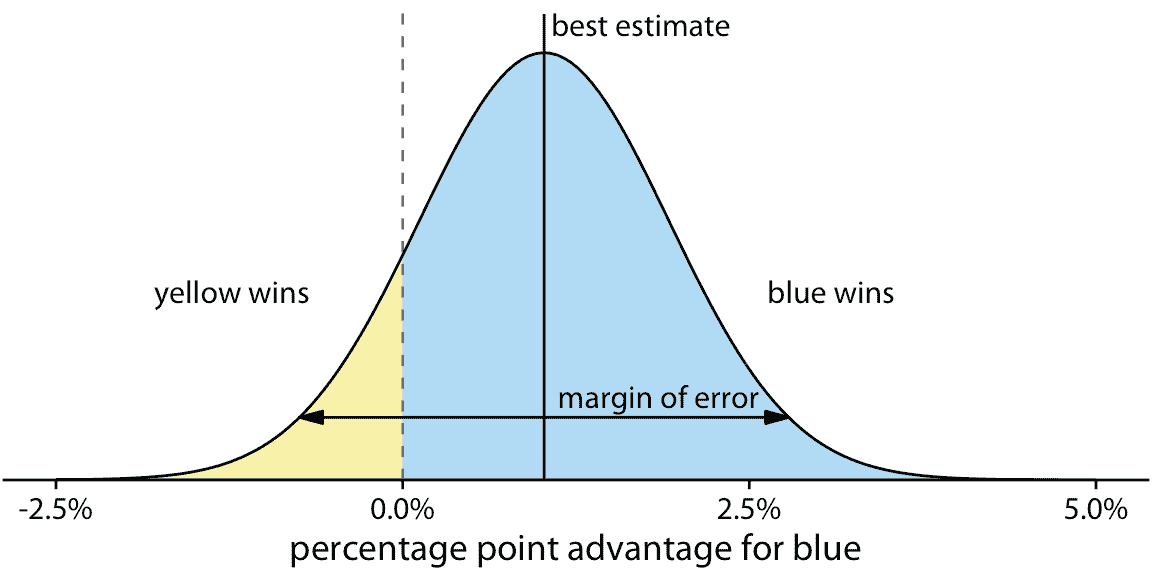  圖 16.2：選舉結果的假設預測。預計藍方將贏得黃方約一個百分點（標記為“最佳估計值”），但該預測存在誤差幅度（它覆蓋 95% 的可能結果，以最佳預測為中心，兩個方向上的 1.76 個百分點）。藍色陰影區域占總數的 87.1%，代表藍色獲勝的所有結果。同樣，黃色陰影區域占總數的 12.9%，代表黃色獲勝的所有結果。在這個例子中，藍色有 87% 的機會贏得選舉。 通過做一些數學計算，我們可以計算出，對于我們的例子，黃方獲勝的幾率是 12.9%。因此，黃方獲勝的幾率比圖 16.1 中顯示的 10% 幾率情況要好一些。如果你喜歡藍方，你可能不會過于擔心，但黃方有足夠的獲勝幾率，他們可能碰巧成功。如果將圖 16.2 與圖 16.1 進行比較，您可能會發現圖 16.1 在結果中創造了更好的不確定性的感覺，即使陰影區域在圖 16.2 準確地表示藍方或黃方獲勝的概率。這是離散結果可視化的力量。對人類感知的研究表明，我們在識別，計數和判斷離散物體的相對頻率方面要好得多 - 只要它們的總數不是太大 - 而不是判斷不同區域的相對大小。 我們可以通過繪制分位數點圖（Kay 等人 2016）將圖 16.1 的離散結果性質與圖 16.2 中的連續分布相結合）。在分位數點圖中，我們將曲線下的總面積細分為均勻大小的單位，并將每個單位繪制為圓形。然后我們堆疊圓形使得它們的排列大致代表原始分布曲線（圖 16.3 ）。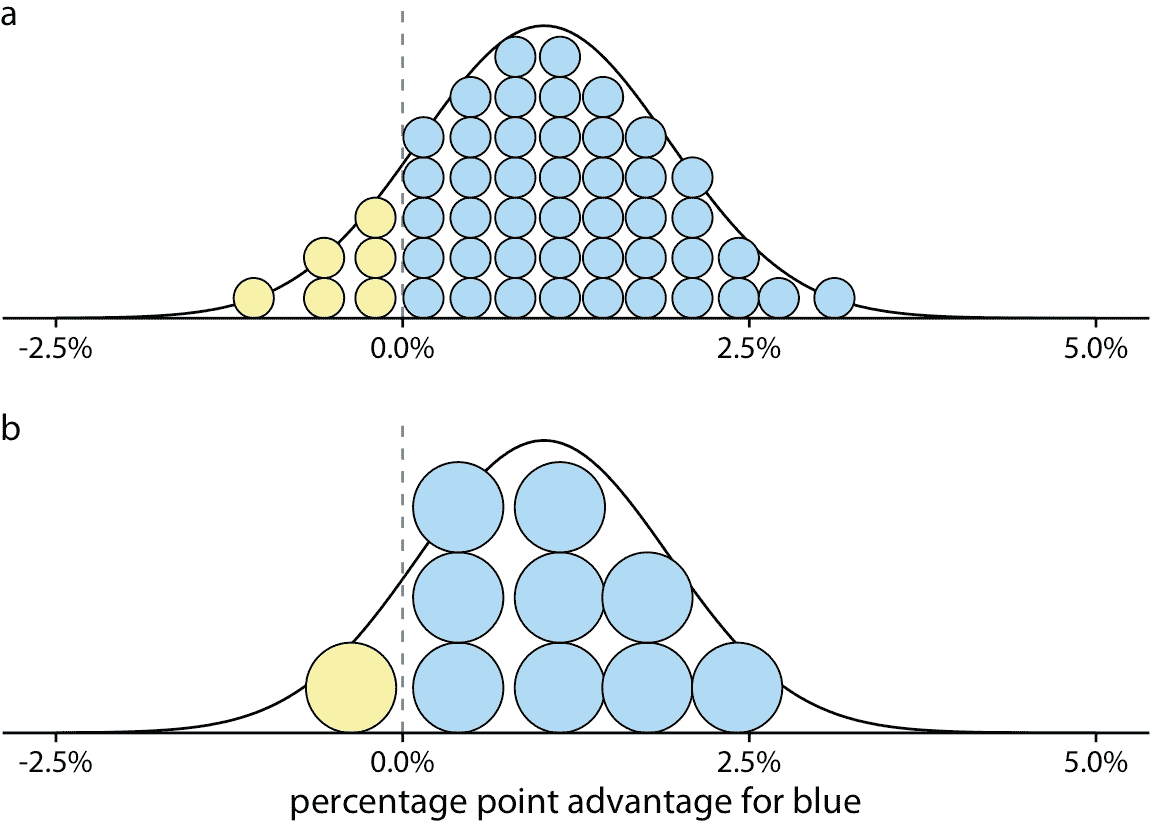  圖 16.3：圖 16.2 的選舉結果分布的分位數點圖形示。 （a）平滑分布用 50 個點近似，每個代表 2% 的幾率。因此，六個黃點對應的概率為 12%，合理接近 12.9% 的真實值。 （b）平滑分布近似為 10 個點，每個點幾率為 10%。因此，一個黃點對應 10% 的幾率，仍然接近真實值。具有較少數量點的分位數點圖往往更容易閱讀，因此在該示例中，10 點版本可能優于 50 點版本。 作為一般原則，分位點點圖應使用小到中等數量的點。如果點太多，那么我們傾向于將它們視為連續體而不是單獨的離散單位。這抵消了離散圖的優點。圖 16.3 顯示具有 50 個點（圖 16.3a）和 10 個點（圖 16.3b）的變體。雖然 50 個點的版本更準確地捕獲真實的概率分布，但是點的數量太大而不能容易地區分各個點。十個點的版本立即傳達了藍方或黃方獲勝的相對幾率。對十個點的版本的一個缺陷可能是它不是很精確。我們對黃方獲勝的幾率過少表示為 2.9 個百分點。然而，通常值得犧牲一些數學精度，來獲得所得可視化的更準確的人類感知，特別是在與非專業讀者進行交流時。在數學上正確但感知上不正確的可視化在實踐中沒有用。 ## 16.2 可視化點估計的不確定性 在圖 16.2 中，我顯示了“最佳估計值”和“誤差幅度”，但我沒有解釋這些量究竟是什么或者如何獲得它們。為了更好地理解它們，我們需要快速介紹統計抽樣的基本概念。在統計數據中，我們的首要目標是通過查看世界的一小部分來了解世界。繼續選舉的例子，假設有許多不同的選區，每個選區的公民都要為藍方或黃方投票。我們可能想要預測每個選區的投票方式，以及各地區的整體投票均值（平均值）。為了在選舉前做出預測，我們不能對每個選區的每個公民進行民意調查，來了解他們將如何投票。相反，我們必須輪詢選區子集的公民子集，并使用這些數據得出最佳猜測。在統計語言中，所有選區所有公民的可能投票總數稱為總體，我們調查的公民和/或選區的子集是樣本。總體代表了世界的潛在真實狀態，樣本是我們進入這個世界的窗口。 我們通常對匯總總體重要屬性的具體數量感興趣。在選舉的例子中，這些可能是跨選區的投票結果的均值或選區結果之間的標準差。描述總體的數量稱為參數，并且它們通常是不可知的。但是，我們可以使用樣本來猜測真實參數值，統計學家將這些猜測稱為估計值。樣本均值是總體均值的估計值，這是一個參數。各個參數值??的估計值也稱為點估計，因為每個參數值可以由線上的點表示。 圖 16.4 顯示了這些關鍵概念如何相互關聯。興趣變量（例如，每個選區的投票結果）在總體中具有一些分布，總體具有總體平均值和總體標準差。樣本將包含一組特定的觀測值。樣本中單個觀測值的數量稱為樣本大小。從樣本中我們可以計算樣本均值和樣本標準差，這些通常與總體均值和標準差不同。最后，我們可以定義采樣分布，如果我們多次重復采樣過程，它是我們將獲得的估計分布。采樣分布的寬度稱為標準誤差，它告訴我們估計的精確程度。換句話說，標準誤差提供了與我們的參數估計值相關的不確定性的度量。作為一般規則，樣本量越大，標準誤差越小，因此估計的不確定性越小。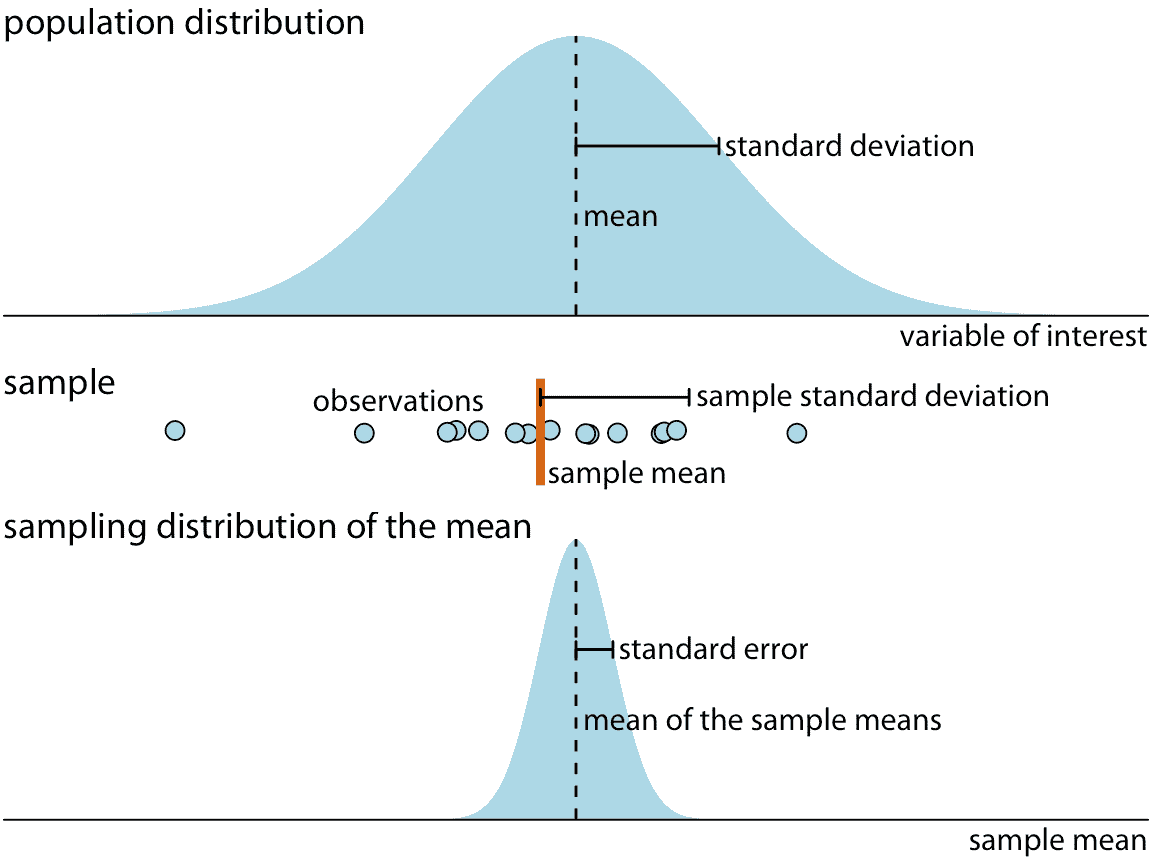  圖 16.4：統計抽樣的關鍵概念。我們正在研究的興趣變量在總體中具有一些真實的分布，具有真實的總體平均值和標準差。該變量的任何有限樣本將具有樣本均值和標準差，與總體參數不同。如果我們每次重復采樣并計算平均值，則所得均值遵循均值的采樣分布。標準誤差提供采樣分布寬度的信息，告訴我們估計興趣參數（這里是總體平均值）的準確程度。 至關重要的是，我們不要混淆標準差和標準誤差。標準差是總體的屬性。它告訴我們，我們可以做出的個別觀測值的分散程度。例如，如果我們考慮投票區的總體，標準差告訴我們不同的選域的差異是多少。相比之下，標準誤差告訴我們，我們確定參數估計值的準確程度。如果我們想估計所有選區的投票結果均值，那么標準誤差會告訴我們對均值的估計有多準確。 所有統計學家都使用樣本來計算參數估計值及其不確定性。然而，他們將這些計算方式分為貝葉斯主義者和頻率論者。貝葉斯假設他們對世界有一些先驗知識，他們使用樣本來更新這些知識。相比之下，頻率論者試圖在沒有任何先驗知識的情況下，對世界做出精確的陳述。幸運的是，當涉及可視化不確定性時，貝葉斯和頻率論者通常可以采用相同類型的策略。在這里，我將首先討論頻率論方法，然后描述貝葉斯環境特有的一些特定問題。 頻率論者最常用誤差條來表示不確定性。雖然誤差條可用作不確定性的可視化，但它們并非沒有問題，我在第九章中已經提到（見圖 9.1 ）。讀者很容易對誤差條代表什么感到困惑。為了突出這個問題，在圖 16.5 中，我展示了同一數據集的誤差條的五種不同用法。該數據集包含巧克力棒的專家評級，針對在許多不同國家制造的巧克力棒，評級為 1 至 5。對于圖 16.5 ，我提取了加拿大制造的巧克力棒的所有評級。樣本顯示為分散點的條帶圖，在它下方，我們看到樣本均值加/減樣本標準差，樣本均值加/減標準誤差，以及 80%，95% 和 99% 置信區間。所有五個誤差條都來自樣本中的變化，它們都是數學上相關的，但它們具有不同的含義。它們在視覺上也非常獨特。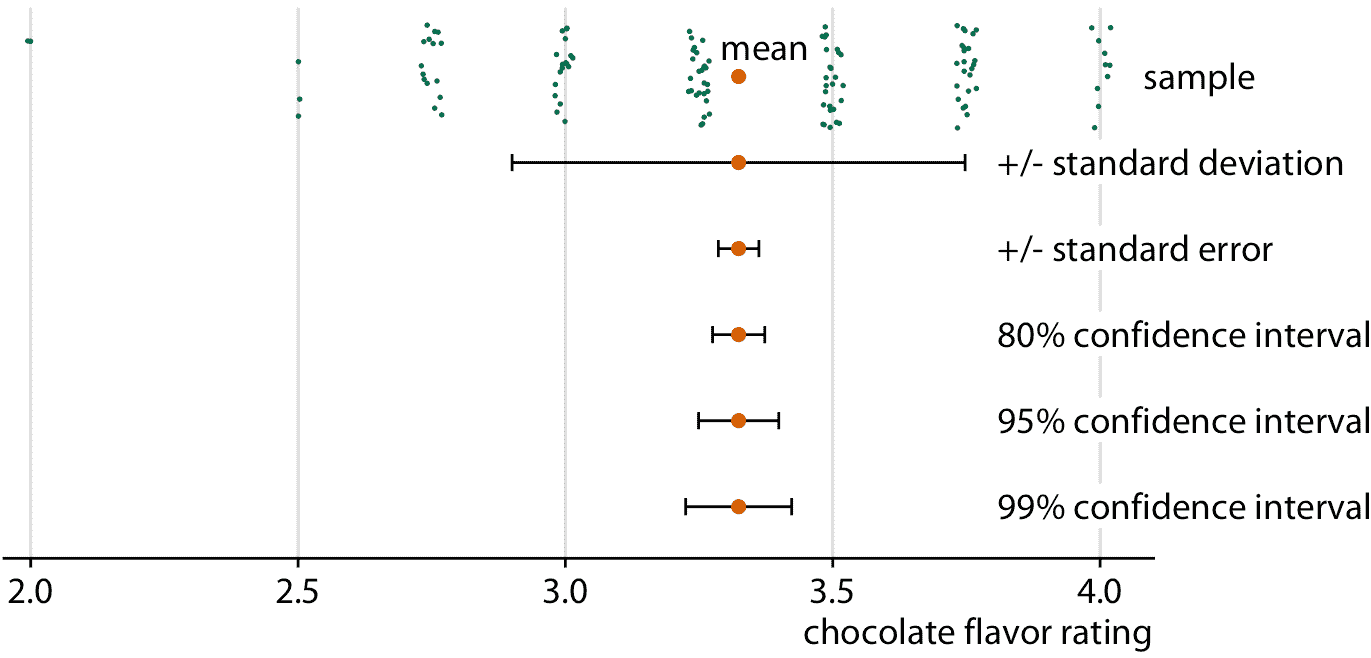  圖 16.5：巧克力棒評級示例中的樣本，樣本均值，標準差，標準誤差和置信區間之間的關系。組成樣本的觀測值（顯示為分散的綠點）代表來自加拿大制造商的 125 個巧克力棒的專家評級，評級從 1（最差）到 5（最好）。較大橙色點代表評級的平均值。誤差條從上到下表示標準差的兩倍，標準誤差的兩倍（平均值的標準差），以及平均值的 80%，95% 和 99% 置信區間。數據來源：曼哈頓巧克力學會 Brady Brelinski 每當您使用誤差條顯示不確定性時，您必須指定誤差條表示的數量和/或置信度。 標準誤差近似為樣本標準差除以樣本大小的平方根，置信區間是通過將標準誤差乘以小的常數值來計算的。例如，95% 置信區間在平均值的任一方向上延伸約為標準誤差的兩倍。因此，較大的樣本往往具有較窄的標準誤差和置信區間，即使它們的標準差相同。當我們比較加拿大巧克力棒和瑞士巧克力棒的評級時，我們可以看到這種效應（圖 16.6 ）。加拿大和瑞士巧克力棒的評級均值和樣本標準差相當，但我們對 125 加拿大棒和 38 瑞士棒進行評級，因此瑞士棒的均值的置信區間要寬得多。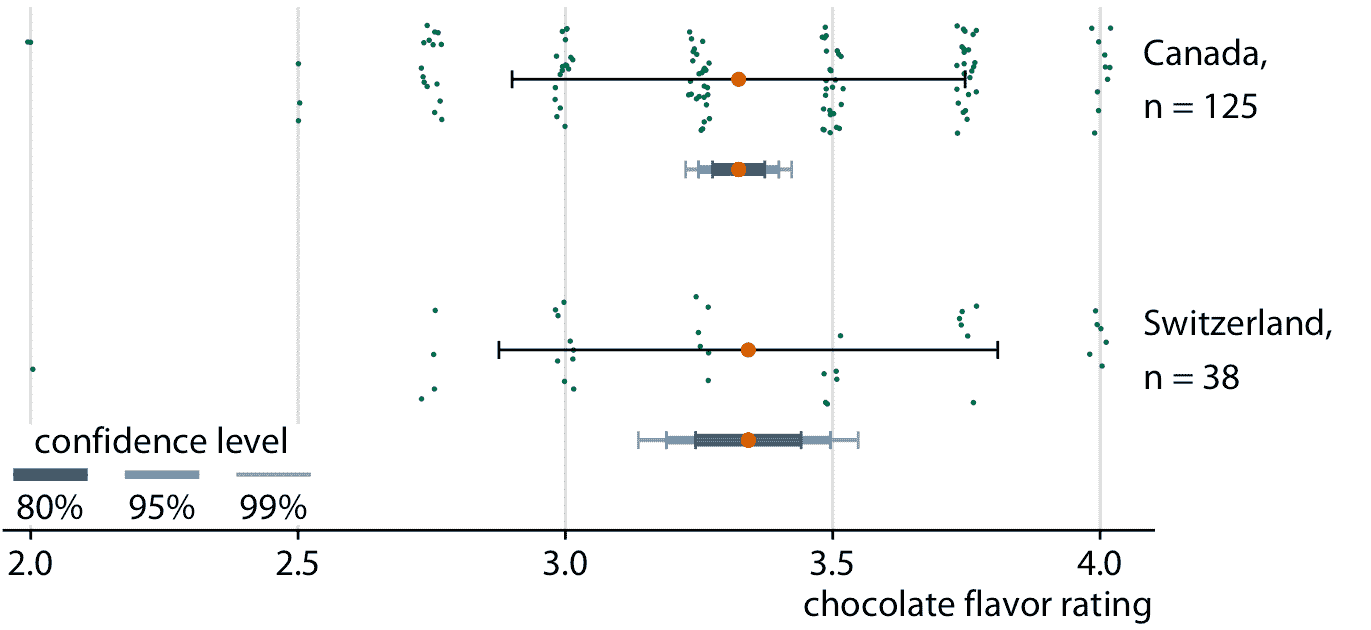  圖 16.6：隨著樣本量的縮小，置信區間變寬。來自加拿大和瑞士的巧克力棒具有可比較的評級均值和可比較的標準差（用簡單的黑色誤差條表示）。然而，被評級的加拿大巧克力棒是瑞士的三倍，因此瑞士的評級均值（用不同顏色和厚度的誤差條表示）的置信區間，比加拿大要寬。數據來源：曼哈頓巧克力學會 Brady Brelinski 在圖 16.6 中，我同時顯示三個不同的置信區間，使用較暗的顏色和較粗的線條表示較低置信度的區間。我將這些可視化稱為分級誤差條。分級有助于讀者認識到存在一系列不同的可能性。如果我向一組人顯示簡單的誤差條（沒有分級），則至少其中一些人可能會以確定性的方式感知誤差條，例如表示數據的最小值和最大值。或者，他們可能認為誤差條描繪了參數估計值的可能范圍，即，估計值永遠不會落在誤差條之外。這些類型的誤解稱為確定性解釋錯誤。我們越能將確定性解釋錯誤的風險降至最低，我們對不確定性的可視化就越好。 誤差條很方便，因為它們允許我們同時顯示許多估計值及其不確定性。因此，它們通常用于科學出版物，其主要目標通常是向專業讀者傳達大量信息。作為此類應用的一個例子，圖 16.7 顯示了在六個不同國家生產的巧克力棒的巧克力評級均值和相關置信區間。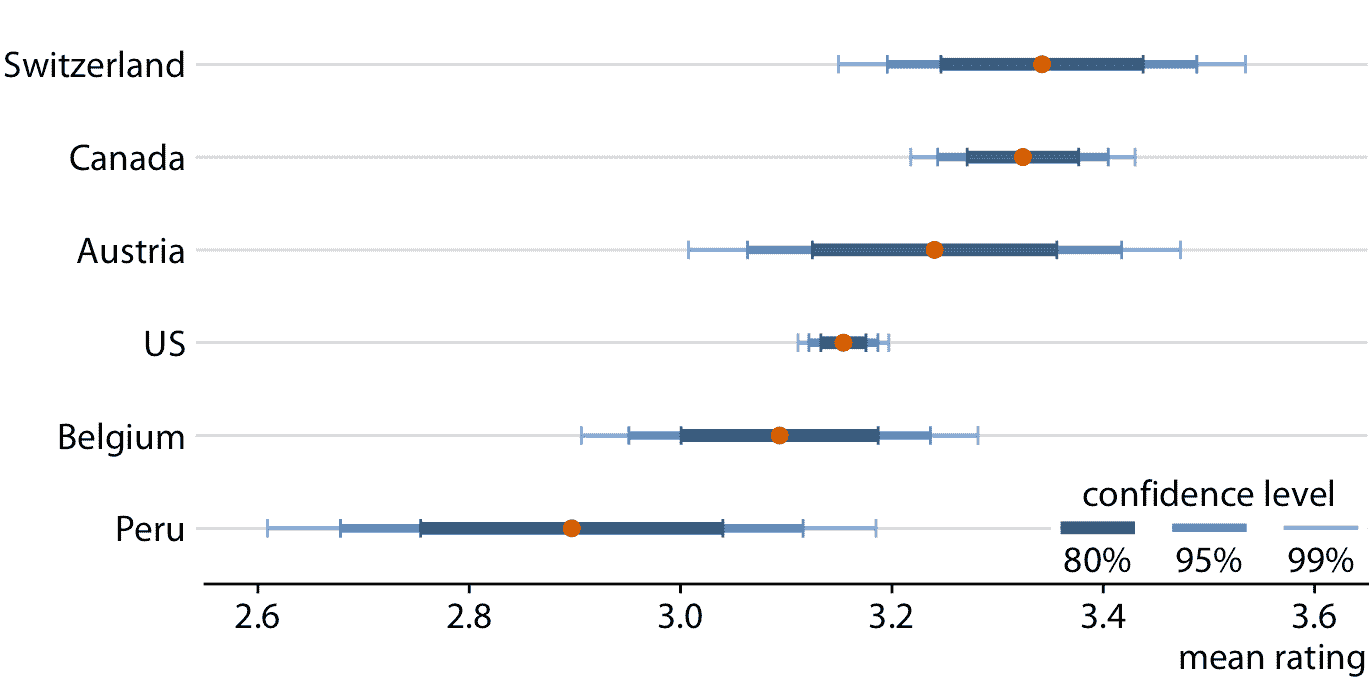  圖 16.7：來自六個不同國家的制造商的巧克力棒的巧克力風味評級均值和相關置信區間。數據來源：曼哈頓巧克力學會 Brady Brelinski 在查看圖 16.7 時，您可能想知道，它告訴我們關于評級均值的差異的什么事情。加拿大，瑞士和奧地利的評級均值高于美國，但考慮到這些評級均值的不確定性，均值有顯著差異嗎？這里的“顯著”一詞是統計學家使用的技術術語。如果我們有一定程度的置信度，可以拒絕觀察到的差異是由隨機抽樣引起的假設，我們稱差異顯著。由于僅僅有限數量的加拿大和美國巧克力棒得到了評級，評估者可能會意外地考慮更多更好的加拿大巧克力棒和更少更好的美國巧克力棒，而這種隨機幾率可能像是加拿大對美國巧克力棒的系統評級優勢。 評估圖 16.7 的顯著性是困難的，因為加拿大和美國的評級均值都有不確定性。兩個不確定性都對均值是否不同很重要。統計教科書和在線教程有時會發布，如何根據誤差條重疊或不重疊的程度來判斷重要性的經驗法則。但是，這些經驗法則不可靠，應該避免。評估評級均值是否存在差異的正確方法是計算差異的置信區間。如果這些置信區間不包括零，那么我們知道在相應的置信水平上差異是顯著的。對于巧克力評級數據集，我們看到只有來自加拿大巧克力棒的評級明顯高于美國（圖 16.8）。對于瑞士的巧克力棒，差異的 95% 置信區間幾乎不包括零值。因此，美國和瑞士巧克力棒的評級均值之間的差異在 5% 水平上幾乎不顯著。最后，根本沒有證據表明奧地利巧克力棒的評級均值系統高于美國。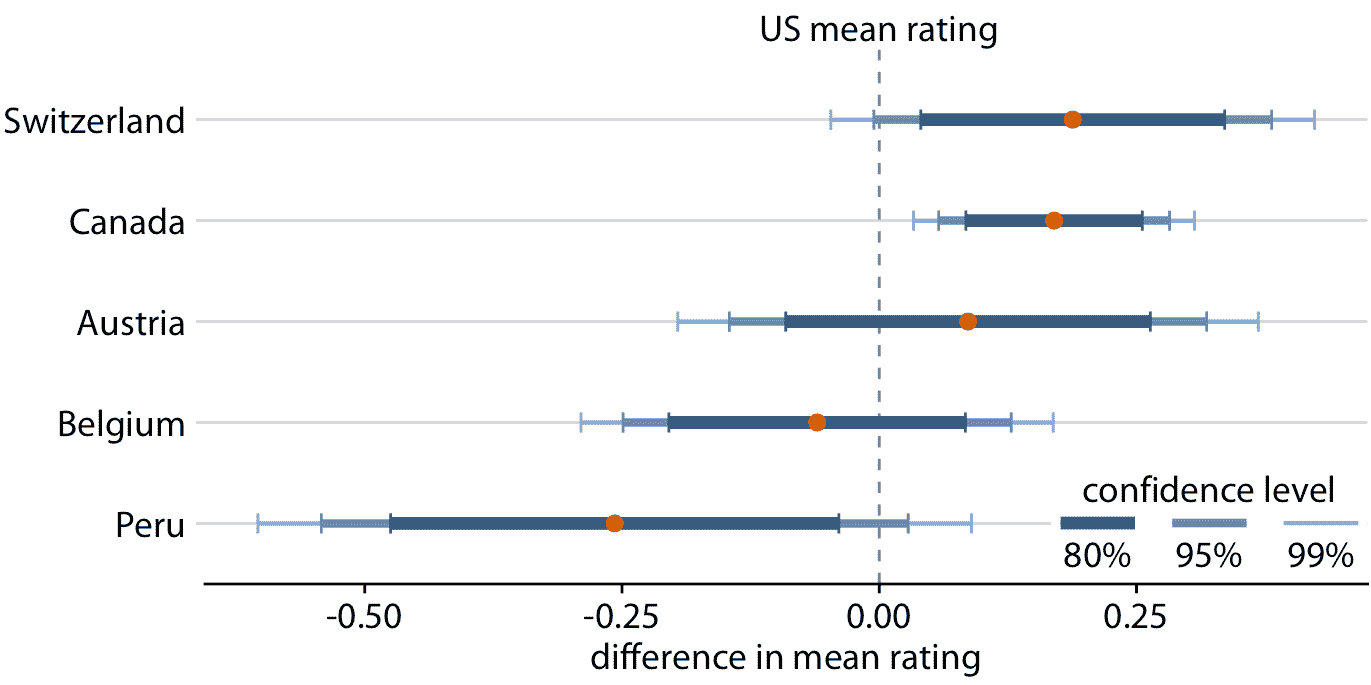  圖 16.8：來自五個不同國家的制造商的巧克力風味評級均值，相對于美國巧克力棒的評級均值。加拿大巧克力棒的評級明顯高于美國。對于其他四個國家，在 95% 置信水平下，與美國的評級均值沒有顯著差異。使用 Dunnett 方法對多個比較調整了置信水平。數據來源：曼哈頓巧克力學會 Brady Brelinski 在前面的圖中，我使用了兩種不同類型的誤差條，分級和簡單。更多變體是可能的。例如，我們可以在末尾繪制帶或不帶帽子的誤差條（圖 16.9a，c 對比圖 16.9b，d）。所有這些選擇都有優點和缺點。分級誤差條突出顯示對應于不同置信水平的不同區間的存在。然而，這些附加信息的另一面是增加了視覺噪聲。根據圖形的復雜程度和信息密集程度，簡單的誤差條可能優于分級條形圖。是否繪制帶有或不帶帽子的誤差條主要是個人品味的問題。帽子突出顯示誤差條的結束位置（圖 16.9 a，c），而沒有帽子的誤差條同樣強調整個區間范圍（圖 16.9b， d）。此外，再次，帽子增加了視覺噪聲，因此在具有許多誤差條的圖中省略帽子可能是優選的。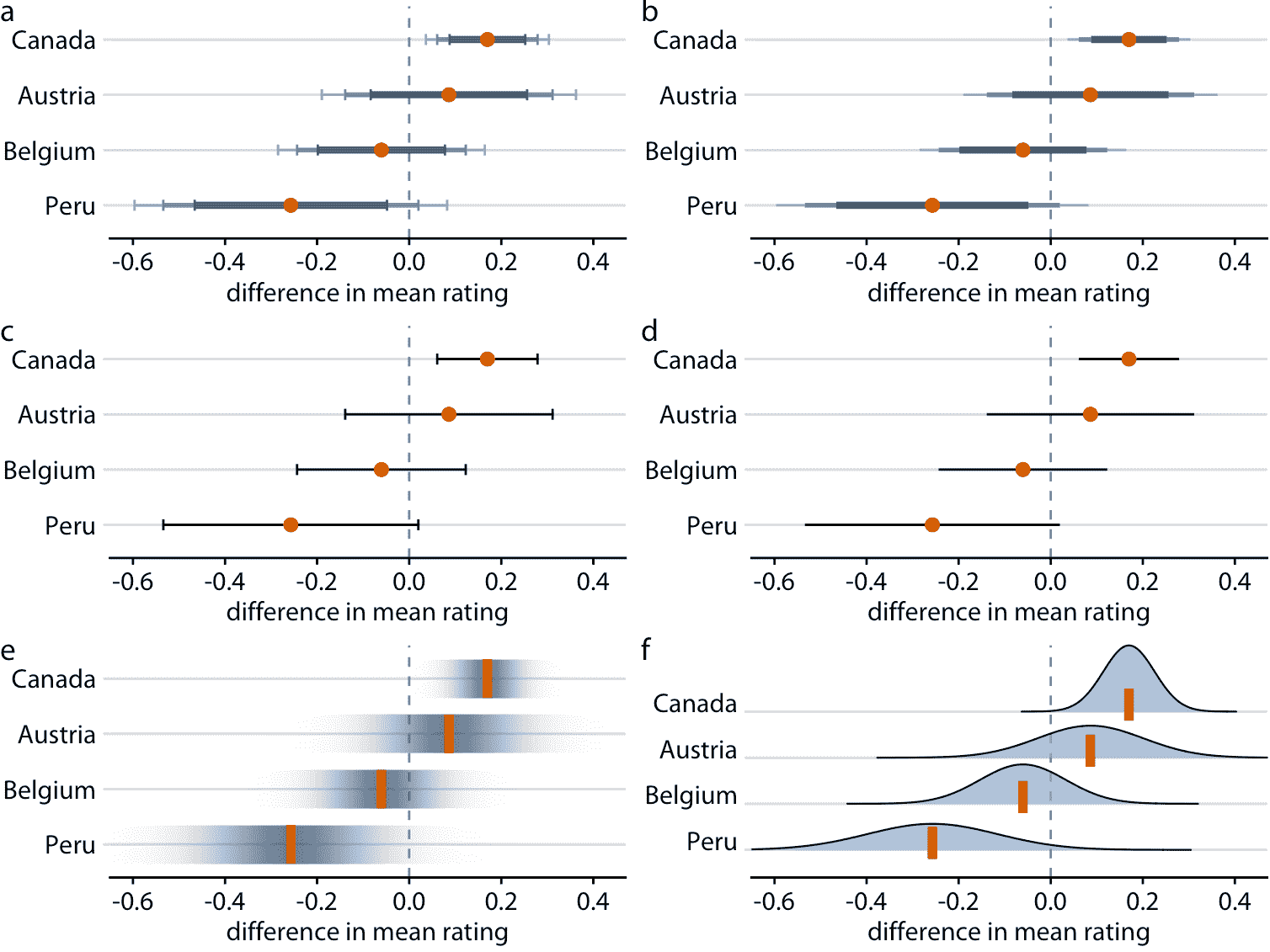  圖 16.9：來自四個不同國家的制造商的巧克力風味評級均值，相對于美國巧克力棒的評級均值。每個面板使用不同的方法來可視化相同的不確定性信息。 （a）帶帽子的分級誤差條。 （b）無帽子的分級誤差條。 （c）帶帽子的單區間誤差條。 （d）無帽子的單區間誤差條。 （e）置信帶。 （f）置信分布。 作為誤差條的替代方案，我們可以繪制逐漸消失的置信帶（圖 16.9 e）。置信帶更好地傳達了不同值的可能性，但它們很難閱讀。我們必須在視覺上整合不同的顏色陰影，來確定特定置信度結束的位置。從圖 16.9 中我們可以得出結論，秘魯巧克力棒的評級均值明顯低于美國巧克力棒，但事實并非如此。當我們顯示明確的置信度分布時會出現類似的問題（圖 16.9 f）。很難在視覺上整合曲線下面積，并確定給定置信水平的確切位置。然而，通過繪制分位數點圖可以稍微減輕這個問題，如圖 16.3。 對于簡單的二維圖形，誤差條比更復雜的不確定性顯示具有一個重要優勢：它們可以與許多其他類型的圖形組合。對于我們可能具有的幾乎任何可視化，我們可以通過添加誤差條來添加一些不確定性指示。例如，我們可以通過繪制帶有誤差條的條形圖，來顯示具有不確定性的數量（圖 16.10）。這種類型的可視化通常用于科學出版物中。我們還可以在散點圖中沿 *x* 和 *y* 方向繪制誤差條（圖 16.11）。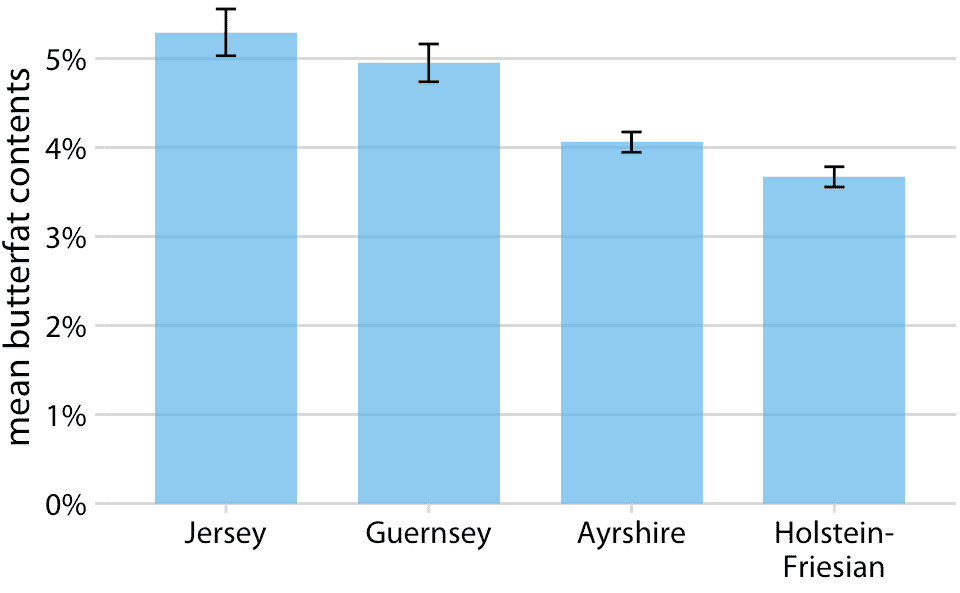  圖 16.10：四種牛的牛奶的平均乳脂含量。誤差條表示平均值加減一個標準誤差。這種可視化在科學文獻中經常出現。雖然它們在技術上是正確的，但它們既不很好地代表每個類別中的變化，也不代表樣本的不確定性。有關單個品種中乳脂含量的變化，請參見圖 7.11。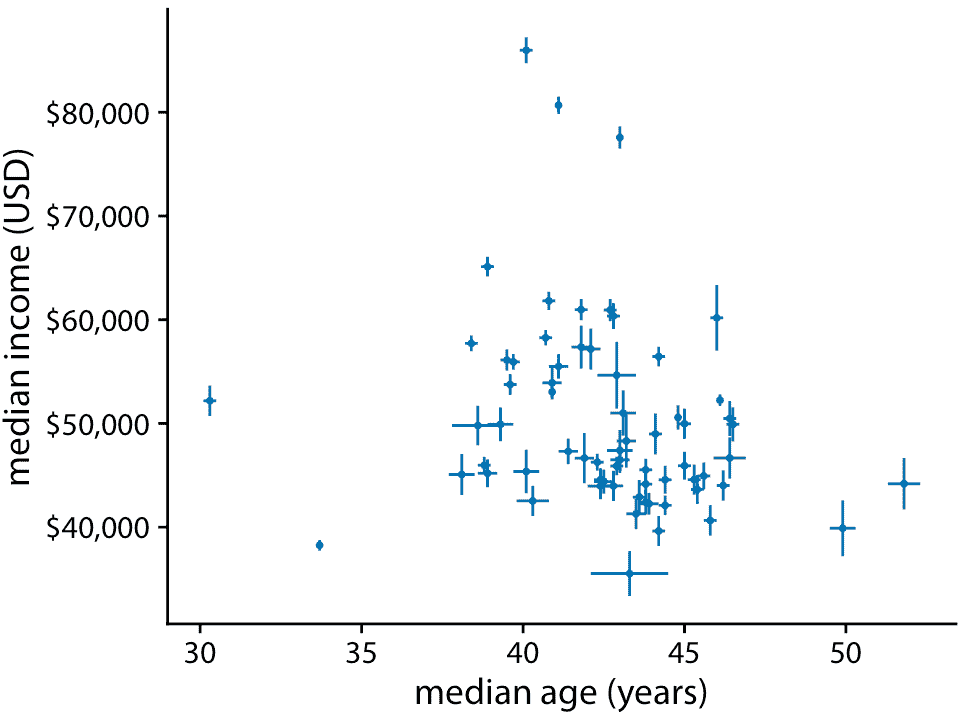數據來源：加拿大純種奶牛的表現記錄  圖 16。11：賓夕法尼亞州 67 個縣的收入中位數與年齡中位數。誤差條表示 90% 置信區間。數據來源：2015 年美國五年社區調查 讓我們回到頻率論者和貝葉斯主義者的話題。頻率論者用置信區間評估不確定性，而貝葉斯學家計算后驗分布和可信區間。貝葉斯后驗分布告訴我們，給定輸入數據的特定參數估計值的可能性。可信區間表示一個值的范圍，參數值以給定概率位于其中，就像從后驗分布中計算一樣。例如，95% 的可信區間對應于后驗分布的中間 95%。真實參數值有 95% 的可能性處于 95% 可信區間。 如果您不是統計學家，您可能會對我對可信區間的定義感到驚訝。您可能認為它實際上是置信區間的定義。它不是。貝葉斯可信區間告訴您真實參數可能在哪里，頻率論置信區間告訴您真實參數可能不在哪里。雖然這種區別可能看起來像語義上的，但兩種方法之間存在重要的概念差異。在貝葉斯方法下，您使用數據和您之前的所研究系統的知識（稱為先驗）來計算概率分布（后驗），告訴您可以預期真實參數值位于哪里。相比之下，在頻率論方法下，你首先假設你打算拒絕。該假設被稱為零（原）假設，并且通常簡單地假設參數等于零（例如，兩個條件之間沒有差異）。然后計算隨機抽樣生成的數據，類似于零假設為真時的觀測數據的概率。置信區間是該概率的表示。如果給定置信區間排除零假設下的參數值（即零值），則可以在該置信水平拒絕零假設。或者，您可以將置信區間視為一個區間，它以指定可能性在重復采樣下捕獲真實參數值（圖 16.12 ）。因此，如果真實參數值為零，則 95% 置信區間僅在 5% 的分析樣本中排除零。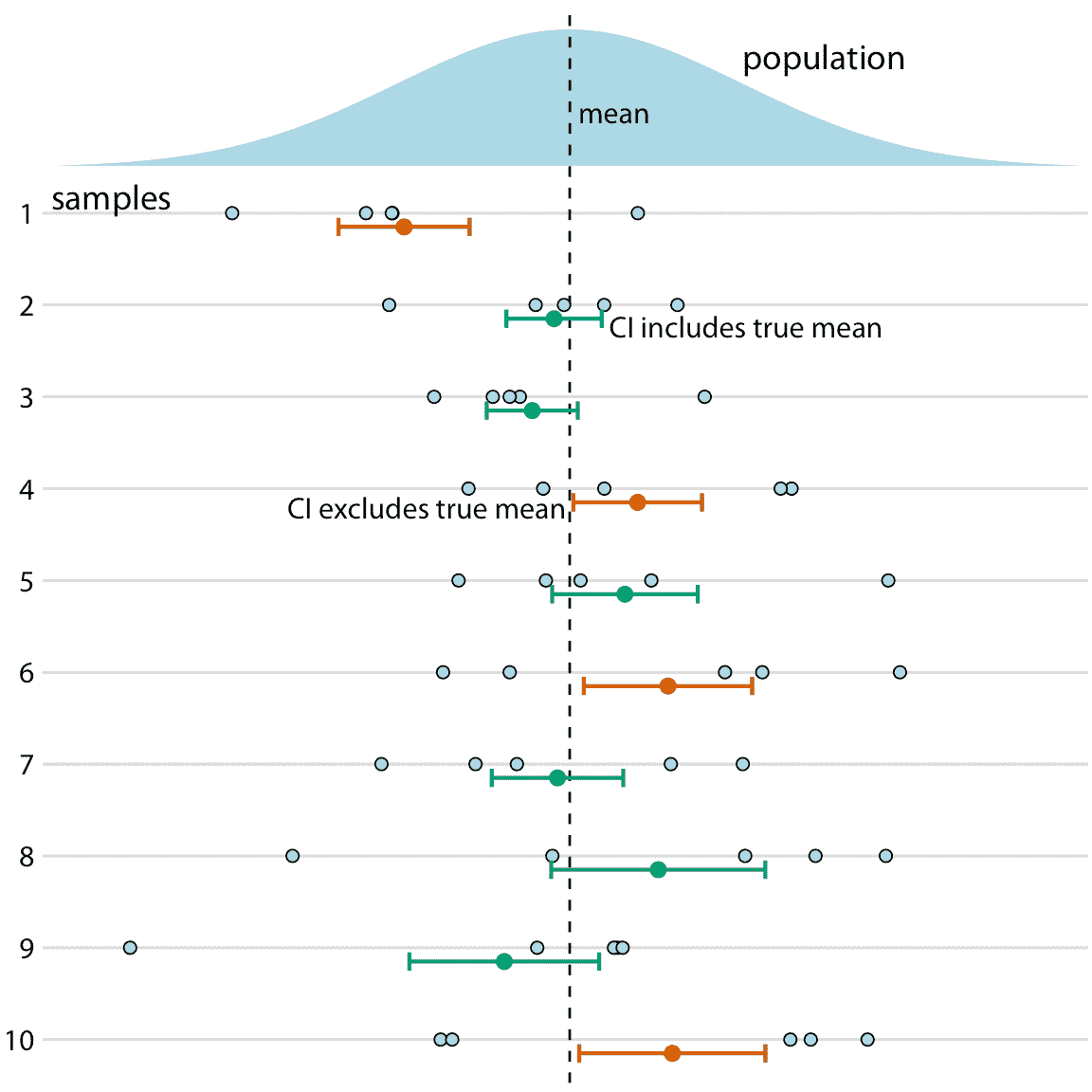  圖 16.12：置信區間的頻率解釋。最好在重復采樣的背景下理解置信區間（CI）。對于每個樣本，特定置信區間包括或排除真實參數，這里是平均值。但是，如果我們重復采樣，那么置信區間（此處顯示為 68% 置信區間，對應于樣本均值+/-標準誤差）在約 68% 的時間中包含真實均值。 總而言之，貝葉斯可信區間對真實參數值進行陳述，頻率置信區間對零假設進行陳述。然而，在實踐中，貝葉斯和頻率論的估計通常非常相似（圖 16.13 ）。貝葉斯方法的一個概念優勢，是它強調思考效果的大小，而頻率論思維強調效果的二元視角，無論是否存在。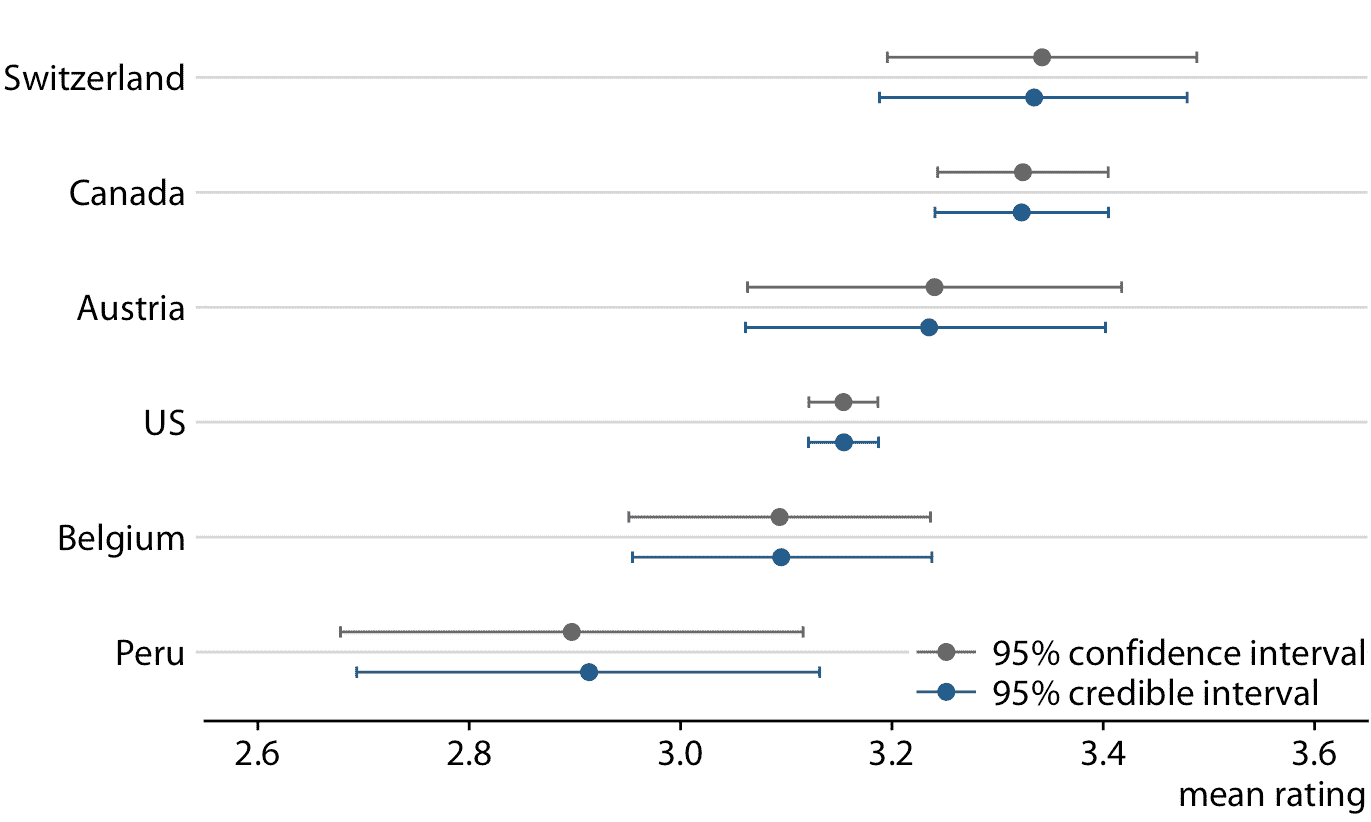  圖 16.13：平均巧克力評級的頻率論置信區間和貝葉斯可信區間的比較。我們看到兩種方法產生相似但不完全相同的結果。特別是，貝葉斯估計顯示出少量的收縮，這是最極端的參數估計在整體均值方向上的調整。 （注意瑞士的貝葉斯估計略微向左移動，秘魯的貝葉斯估計相對于相應的頻率估計稍微向右移動。）此處顯示的頻率估計和置信區間，與圖 16.7 所示的 95% 置信的結果相同。 貝葉斯可信區間回答了這樣一個問題：“我們期望真實參數值位于何處？”頻率主義置信區間回答了一個問題：“我們對于真實參數值不是零的確定程度如何？” 貝葉斯估計的中心目標是獲得后驗分布。因此，貝葉斯通常將整個分布可視化，而不是將其簡化為可信區間。因此，在數據可視化方面，在第七、八、九章中討論的可視化分布的所有方法都是適用的。具體而言，直方圖，密度圖，箱線圖，提琴圖和脊線圖都常用于可視化貝葉斯后驗分布。由于這些方法已經在他們的具體章節中進行了詳細討論，我將在這里僅展示一個例子，使用脊線圖來顯示平均巧克力評級的貝葉斯后驗分布（圖 16.14）。在這個特定情況下，我在曲線下添加了陰影來指示后驗概率的定義區域。作為著色的替代方法，我也可以繪制分位數點圖，或者我可以在每個分布下添加分級誤差條。帶有誤差條的脊線圖稱為半眼圖，帶有誤差條的提琴圖稱為眼圖（章節 5.6）。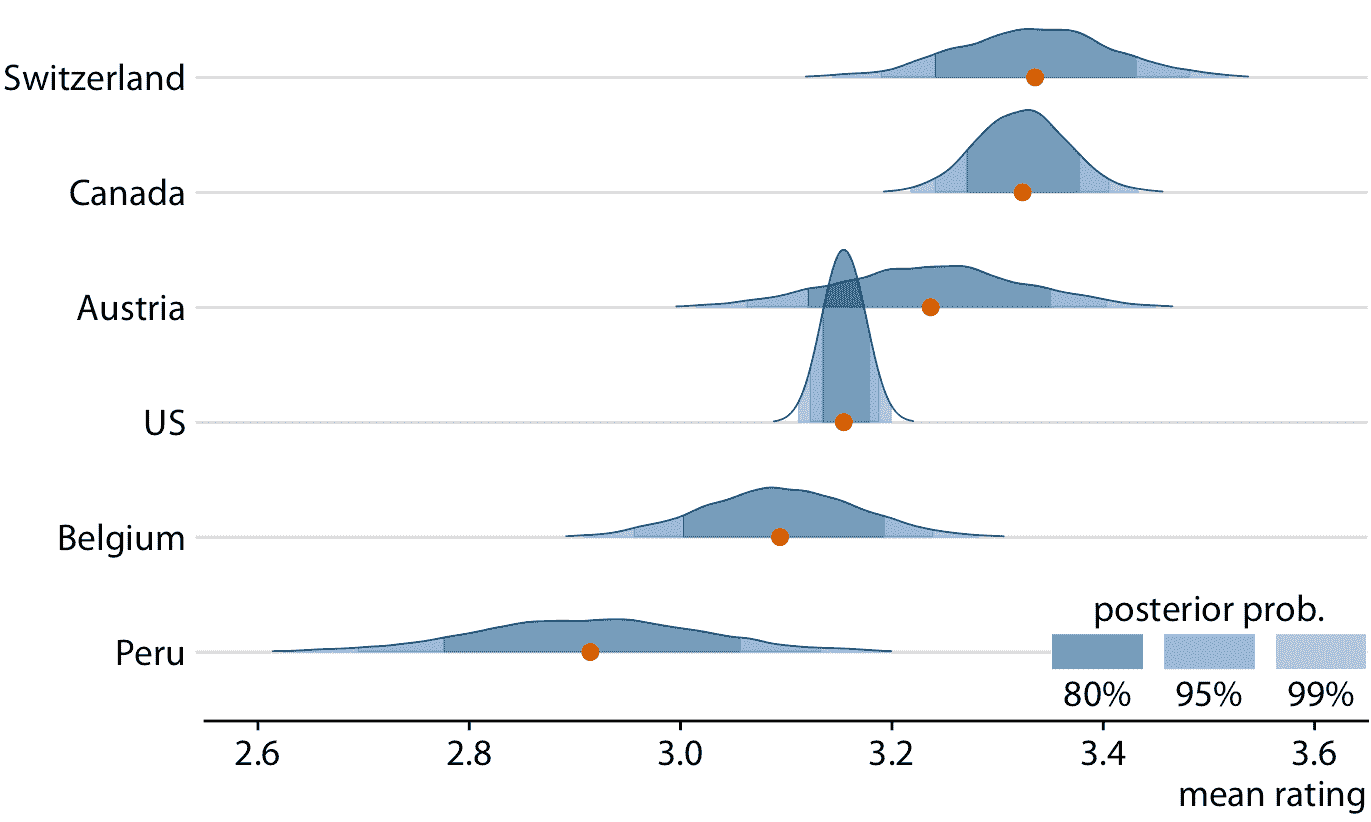  圖 16.14：平均巧克力棒評級的貝葉斯后驗分布，顯示為脊線圖。紅點代表每個后驗分布的中位數。由于難以通過眼睛將連續分布轉換為特定置信區域，因此我在每條曲線下添加了陰影來指示每個后驗分布的中心 80%，95% 和 99%。 ## 16.3 可視化曲線擬合的不確定性 在第 14 章中，我們討論了如何通過將直線或曲線擬合到數據，來顯示數據集中的趨勢。這些趨勢估計也存在不確定性，并且習慣上在具有置信區間的趨勢線中顯示不確定性（圖 16.15）。置信區間為我們提供了一系列與數據兼容的不同擬合線。當學生第一次遇到一個置信區間時，他們常常會驚訝地發現，即使是完美的直線擬合也會產生一個彎曲的置信帶。彎曲的原因是直線擬合可以在兩個不同的方向上移動：它可以上下移動（即，具有不同的截距），并且它可以旋轉（即，具有不同的斜率）。我們可以通過繪制從擬合參數的后驗分布隨機生成的一組替代擬合線，來可視地顯示置信帶是如何產生的。這在圖 16.16 中完成，它顯示了 15 個隨機選擇的替代擬合。我們看到，即使每條線都是完全筆直的，每條線的不同斜率和截距的組合也會產生一個整體形狀，看起來就像置信區間一樣。  圖 16.15：雄性藍鳥的頭長與體重的關系，如圖 14.7 所示。藍色直線代表數據的最佳線性擬合，線周圍的灰色條帶顯示線性擬合的不確定性。灰色條帶代表 95% 的置信水平。數據來源：歐柏林學院的 Keith Tarvin  圖 16.16：雄性藍鳥的頭長與體重的關系。與圖 16.15 相比，藍色直線現在代表從后驗分布中隨機抽取的等可能的替代擬合。數據來源：歐柏林學院的 Keith Tarvin 為了繪制置信帶，我們需要指定置信水平，正如我們在誤差條和后驗概率中看到的那樣，突出不同的置信水平會很有用。這導致我們進入分級置信區間，一次顯示幾個置信水平（圖 16.17 ）。分級置信帶增強了讀者的不確定感，并迫使讀者面對數據可能支持不同替代趨勢線的可能性。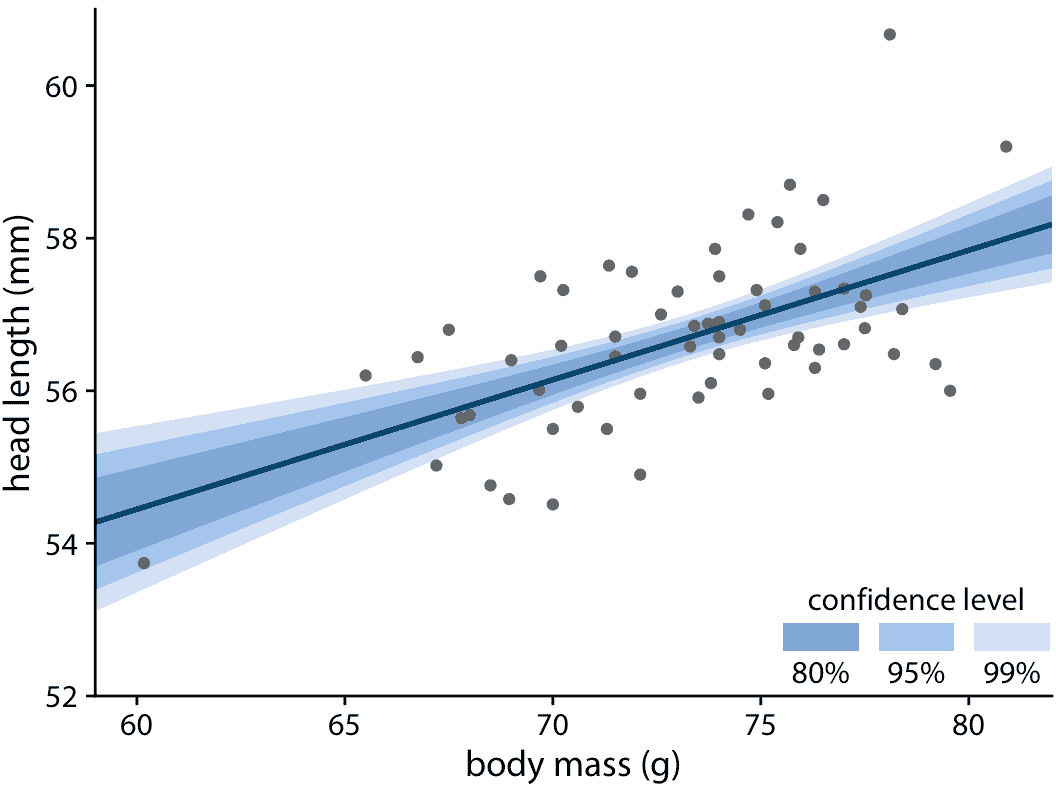  圖 16.17：雄性藍鳥的頭長與體重的關系。與誤差條的情況一樣，我們可以繪制分級置信帶，來突出估計中的不確定性。數據來源：歐柏林學院的 Keith Tarvin 我們還可以繪制非線性曲線擬合的置信區間。這樣的置信區間看起來不錯，但很難解釋（圖 16.18 ）。如果我們看一下圖 16.18a，我們可能會認為，通過向上和向下移動藍線并可能稍微變形來產生置信帶。然而，如圖 16.18b 所揭示的，置信帶表示一系列曲線，它們比部分（a）所示的整體最佳擬合擺動更大。這是非線性曲線擬合的一般原理。不確定性不僅對應于曲線的上下運動，還對應于增加的擺動。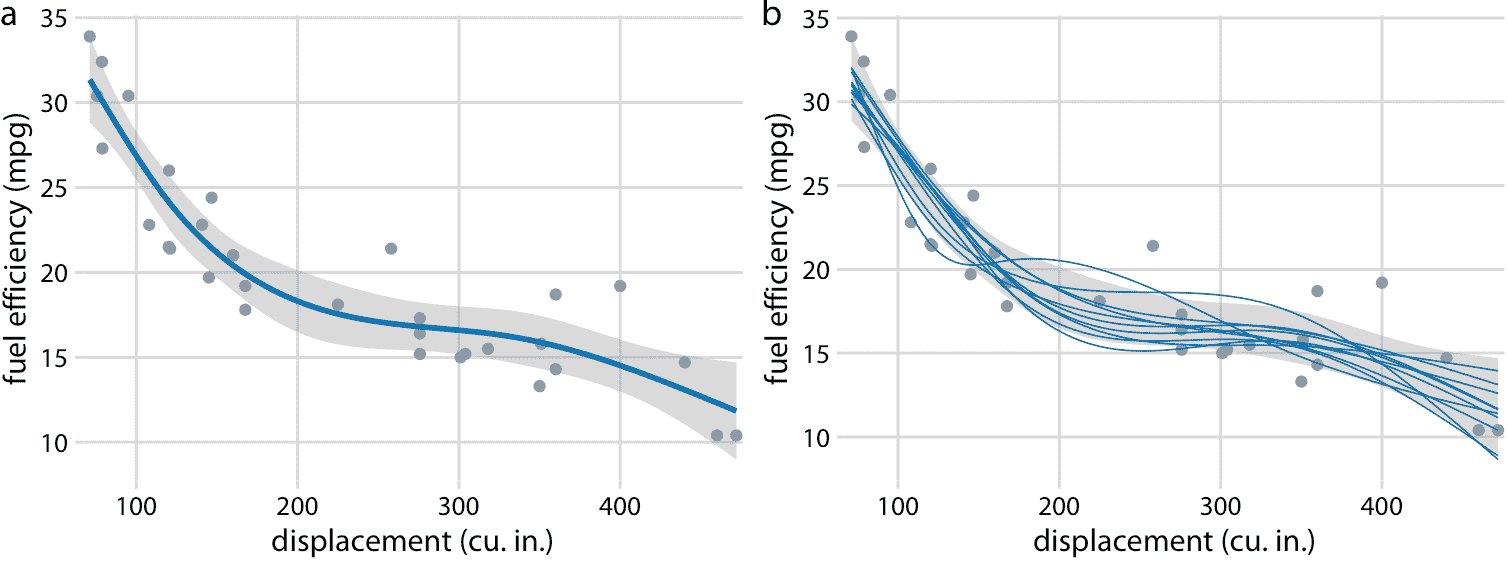  圖 16.18：32 輛汽車（1973-74 型號）的燃油效率與排量的關系。每個點代表一輛汽車，通過擬合 5 節的立方回歸樣條獲得平滑線。 （a）最佳擬合樣條和置信帶。 （b）從后驗分布中抽取的等可能的替代擬合。數據來源：Motor Trend，1974。 ## 16.4 假設結果圖 所有不確定性的靜態可視化都受到以下問題的困擾：讀者可能將不確定性可視化的某些方面，解釋為數據的確定性特征（確定性構造誤差）。我們可以通過動畫來可視化不確定性，通過循環通過許多不同但等可能的繪圖來避免這個問題。這種可視化被稱為假設結果圖（Hullman，Resnick 和 Adar 2015）或 HOP。雖然在打印介質中不可能有 HOP，但它們在在線設置中非常有效，其中動畫可視化可以以 GIF 或 MP4 視頻形式提供。 HOP 在口頭陳述的背景下也可以很好地運作。 為了說明 HOP 的概念，讓我們再回到巧克力棒評級。當您站在雜貨店考慮購買一些巧克力時，您可能不關心某些巧克力棒組的平均風味評級，和相關的不確定性。相反，你可能想知道一個更簡單的問題的答案，例如：如果我隨機拿起一個加拿大和美國制造的巧克力棒，我應該期望哪個更好？為了得到這個問題的答案，我們可以從數據集中隨機選擇加拿大和美國的巧克力棒，比較他們的評級，記錄結果，然后多次重復這個過程。如果我們這樣做，我們會發現在大約 53% 的情況下，加拿大巧克力棒將排名更高，47% 的情況下美國巧克力棒排名更高或兩個并列。我們可以通過在這幾個隨機采樣中循環，在視覺上顯示這個過程，并顯示每次抽取的兩個巧克力棒的相對評級（圖 16.19/16.20）。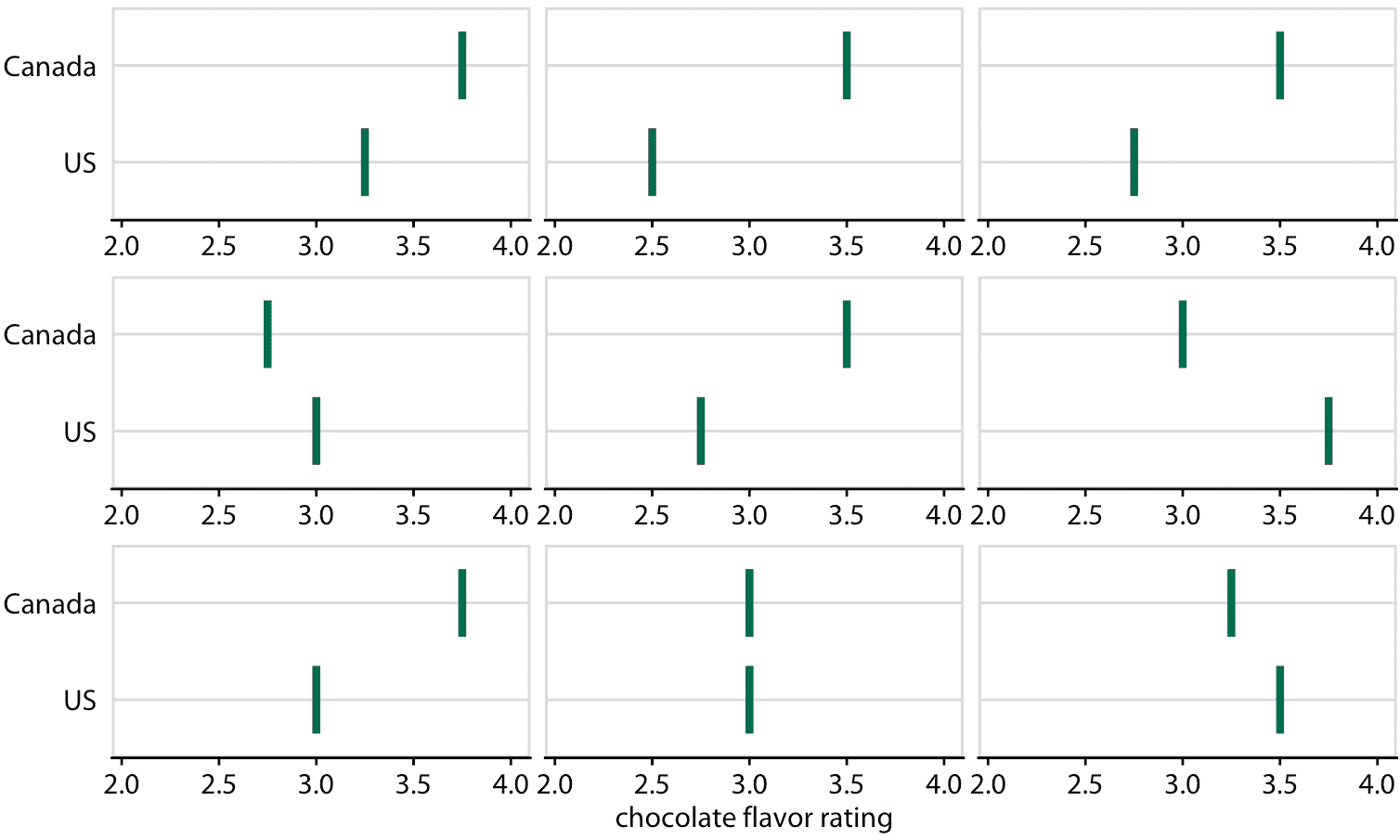  圖 16.19 :（用于印刷版）加拿大和美國巧克力棒評級的假設結果圖示意圖。每個垂直的綠條表示一個巧克力棒的評級，每個面板顯示兩個隨機選擇的巧克力棒的比較，每個巧克力棒來自加拿大制造商和美國制造商。在實際的假設結果圖中，界面將在不同的繪圖面板之間循環，而不是并排顯示它們。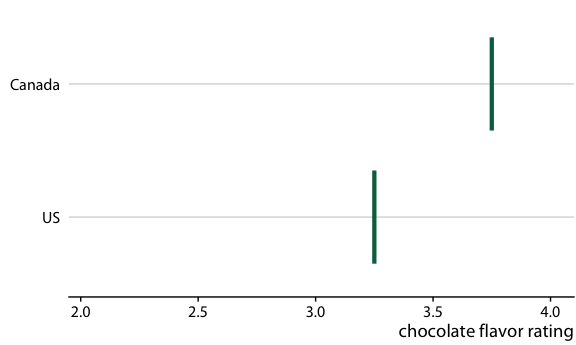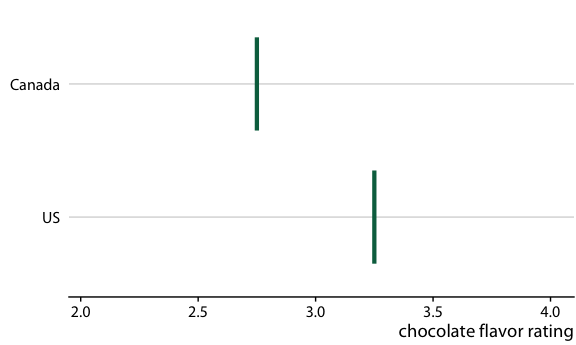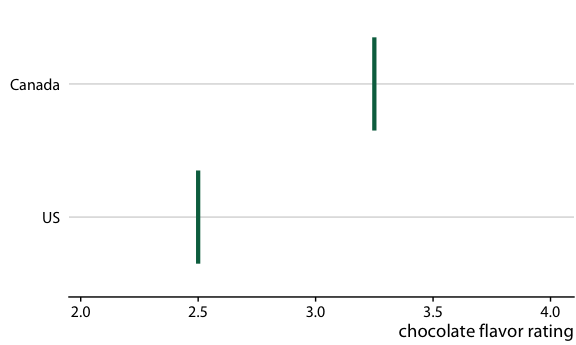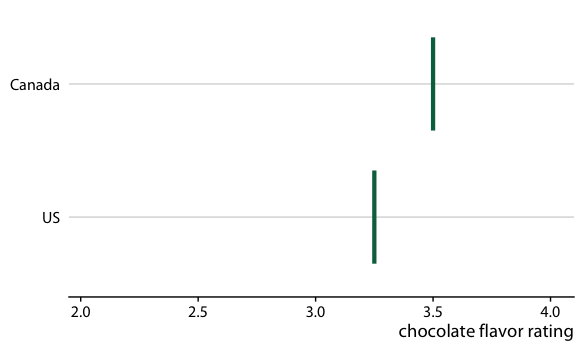  圖 16.20 ：（對于在線版本）加拿大和美國的巧克力棒評級的假設結果圖。每個垂直的綠條表示一個巧克力棒的評級。動畫在兩個隨機選擇的巧克力棒的不同情況之間循環，每個來自加拿大制造商和美國制造商。 作為第二個例子，考慮圖 16.18b 中等可能的趨勢線中的形狀變化。由于所有趨勢線都是相互重疊繪制的，因此我們主要感知趨勢線覆蓋的整體區域，這類似于置信區間。理解各個趨勢線很困難。通過將此圖轉換為 HOP，我們可以一次突出顯示一個趨勢線（圖 16.21/16.22）。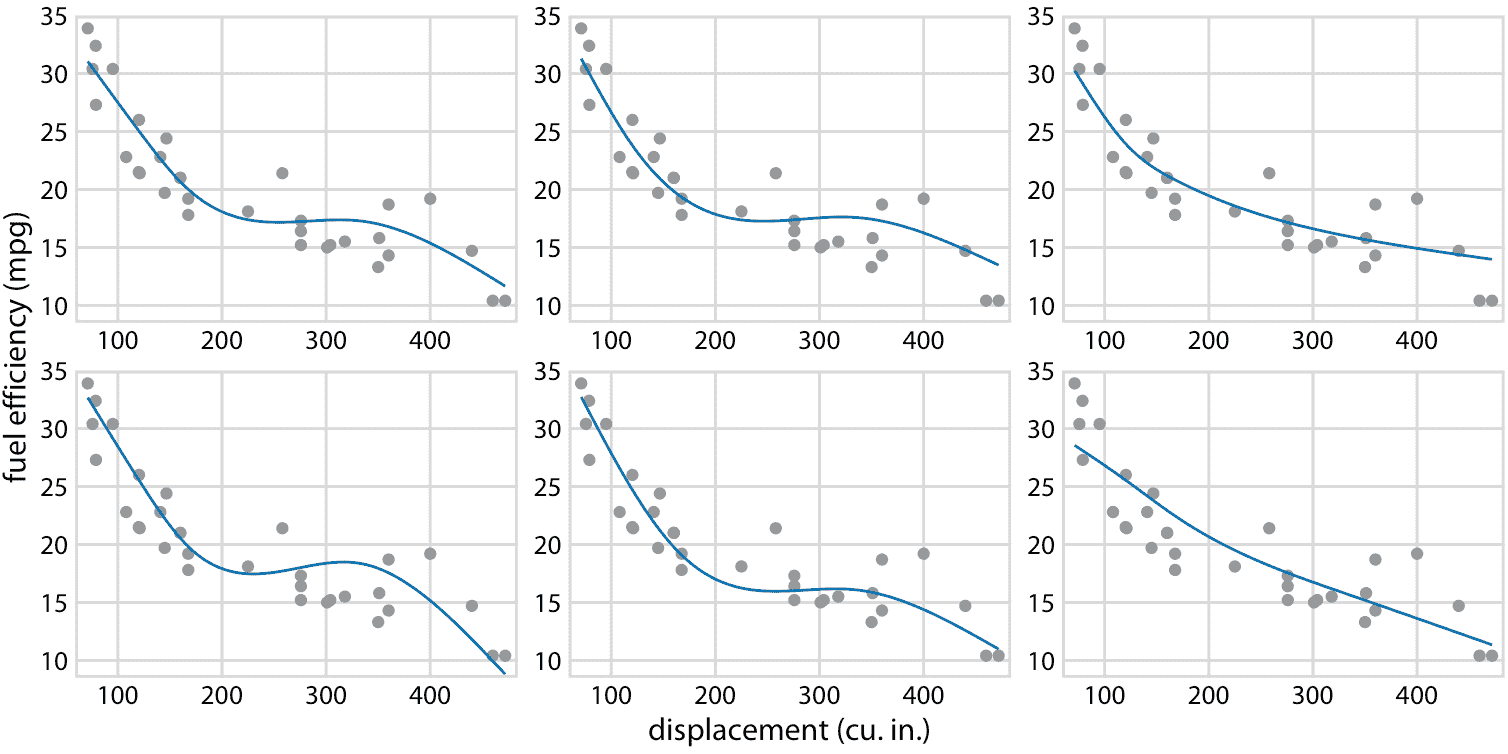  圖 16.21 ：（用于印刷版）燃料效率與排量的假設結果圖示意圖。每個點代表一輛汽車，通過擬合 5 節的立方回歸樣條獲得平滑線。每個面板中的每條線代表一個替代的擬合結果，從擬合參數的后驗分布中抽取。在實際的假設結果圖中，界面將在不同的繪圖面板之間循環，而不是并排顯示它們。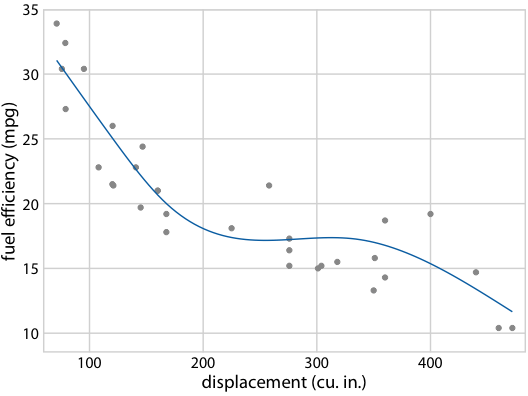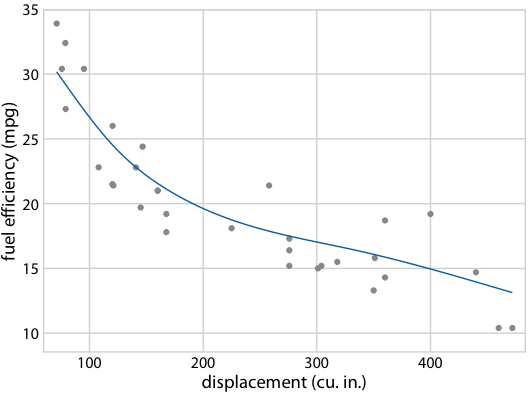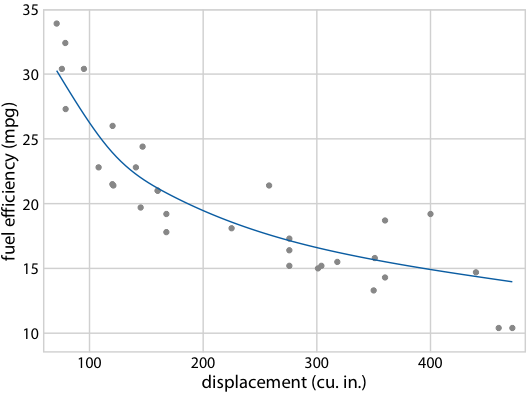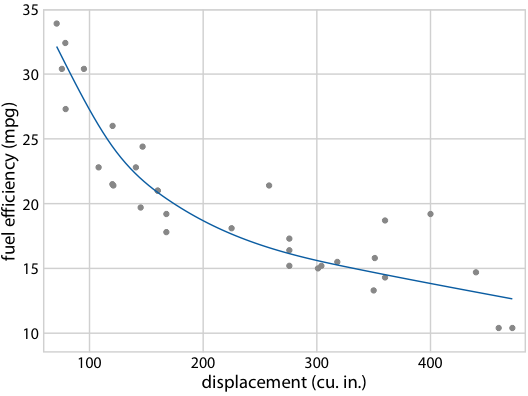  圖 16.22 ：（對于在線版本）燃料效率與排量的假設結果圖。每個點代表一輛汽車，通過擬合 5 節的立方回歸樣條獲得平滑線。界面在不同替代擬合結果之間循環，它們從擬合參數的后驗分布抽取。 在制作 HOP 時，您可能想知道在不同結果之間進行硬切換（如在幻燈片投影儀中），或者從一個結果平滑過渡到下一個結果（例如，將一個結果的趨勢線慢慢變形直到它看起來像另一個結果的趨勢線）是否更好。雖然這在某種程度上是一個需要繼續研究的開放性問題，但一些證據表明，平滑過渡使得更難判斷所代表的概率（Kale 等 [2018](#ref-Kale_et_al_2018) ）。如果您考慮在結果之間制作動畫，您可能希望至少使這些動畫很快，或者選擇一種動畫樣式，其中結果淡入淡出而不是從一個變為另一個。 在制作 HOP 時，我們需要注意一個關鍵方面：我們需要確保我們所展示的結果能夠代表可能結果的真實分布。否則，我們的 HOP 可能會產生誤導。例如，回到巧克力評級的情況下，如果我隨機選擇十對結果巧克力棒，其中美國巧克力棒在七種情況下被評為高于加拿大巧克力棒，那么 HOP 會產生錯誤印象：美國巧克力棒的往往比加拿大巧克力棒評級更高。我們可以通過選擇大量結果來防止這個問題，或者通過某種形式驗證所展示的結果是否合適，因此采樣偏差是不太可能的。在制作圖 16.19/16.20 時，我確認加拿大巧克力棒的獲勝次數接近 53% 的真實百分比。 ### 參考 ``` Kay, M., T. Kola, J. Hullman, and S. Munson. 2016. “When (Ish) Is My Bus? User-centered Visualizations of Uncertainty in Everyday, Mobile Predictive Systems.” CHI Conference on Human Factors in Computing Systems, 5092–5103. doi:10.1145/2858036.2858558. Hullman, J., P. Resnick, and E. Adar. 2015. “Hypothetical Outcome Plots Outperform Error Bars and Violin Plots for Inferences About Reliability of Variable Ordering.” PLOS ONE 10: e0142444. doi:10.1371/journal.pone.0142444. Kale, A., F. Nguyen, M. Kay, and J. Hullman. 2018. “Hypothetical Outcome Plots Help Untrained Observers Judge Trends in Ambiguous Data.” IEEE Transactions on Visualization and Computer Graphics. doi:10.1109/TVCG.2018.2864909. ```