# 14 可視化趨勢
> 原文: [14 Visualizing trends](https://serialmentor.com/dataviz/visualizing-trends.html)
> 校驗:[飛龍](https://github.com/wizardforcel)
> 自豪地采用[谷歌翻譯](https://translate.google.cn/)
在制作散點圖(第 12 章)或時間序列(第 13 章)時,我們通常對數據的總體趨勢更感興趣,而不是每個單獨數據點的位置的具體細節。通過在實際數據點之上或代替實際數據點繪制趨勢,通常以直線或曲線的形式,我們可以創建可視化,幫助讀者立即查看數據的關鍵特征。確定趨勢有兩種基本方法:我們可以通過某種方法平滑數據,例如移動平均值,或者我們可以擬合曲線,它具有所定義的函數形式,然后繪制擬合曲線。一旦我們確定了數據集中的趨勢,特別注意相對于趨勢的偏差,或將數據分成多個成分(包括基礎趨勢,任何現有的循環成分,偶然成分或隨機噪聲)也可能很有用。
## 14.1 平滑
讓我們考慮一下道瓊斯工業平均指數(簡稱道瓊斯)的時間序列,這是一個股票市場指數,代表 30 家大型上市公司的價格。具體來說,我們將看看 2008 年崩盤后的 2009 年(圖 14.1)。在崩盤的末期,2009 年的前三個月,市場損失超過 2400 點(約 27%)。然后它在當年余下的時間里慢慢恢復。我們如何看待這些長期趨勢,同時不再強調不那么重要的短期波動?
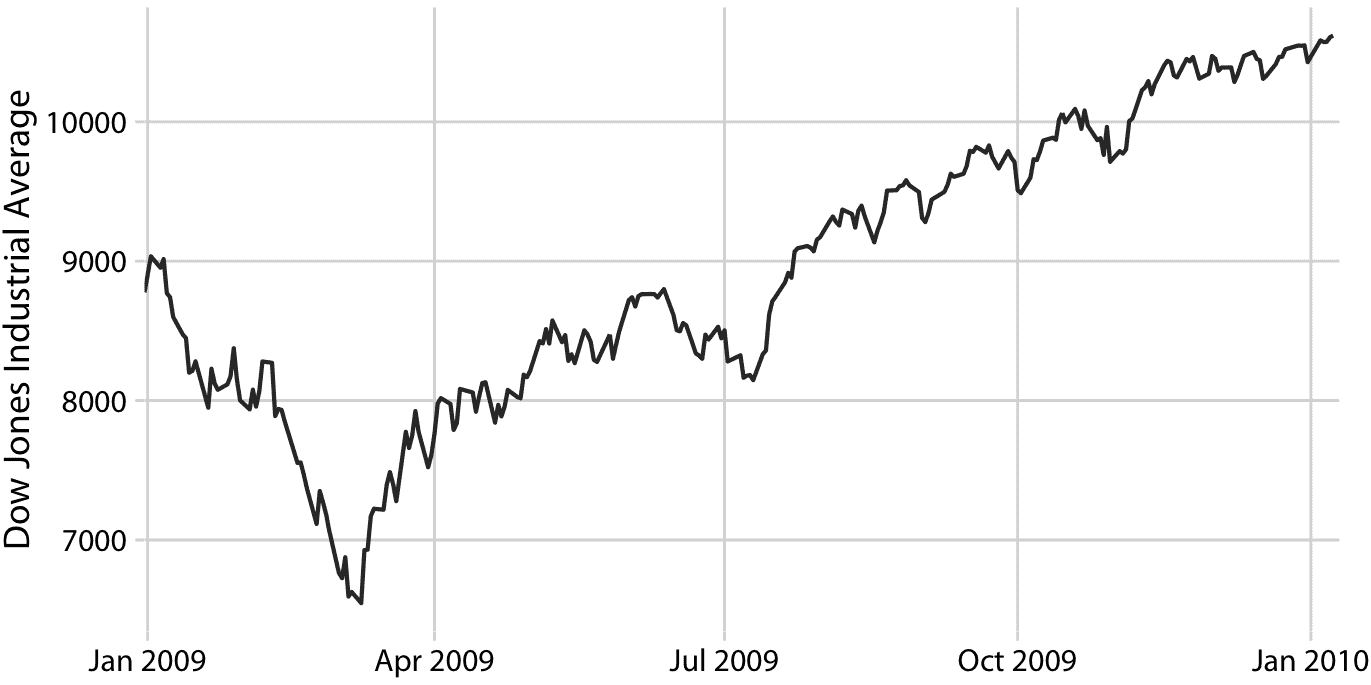
圖 14.1:道瓊斯工業平均指數 2009 年的每日收盤價。數據來源:雅虎金融
在統計方面,我們正在尋找一種方法來平滑股市時間序列。平滑操作產生一個函數,捕獲數據中的關鍵模式,同時去除不相關的細微細節或噪聲。金融分析師通常通過計算移動平均值來平滑股市數據。要生成移動平均值,我們需要一個時間窗口,比如時間序列中的前 20 天,計算這 20 天的平均價格,然后將時間窗口移動一天,所以它現在跨越第 2 天到第 21 天,計算這 20 天的平均值,再次移動時間窗口,依此類推。結果是一個由一系列平均價格組成的新時間序列。
為了繪制這個移動平均值序列,我們需要確定與每個時間窗口的平均值關聯的特定時間點。財務分析師經常在每個時間窗口的末尾繪制每個平均值。這種選擇導致曲線滯后于原始數據(圖 14.2a),更嚴重的滯后對應于更大的平均時間窗口。另一方面,統計學家在時間窗口的中心繪制平均值,這導致曲線完全覆蓋原始數據(圖 14.2b)。
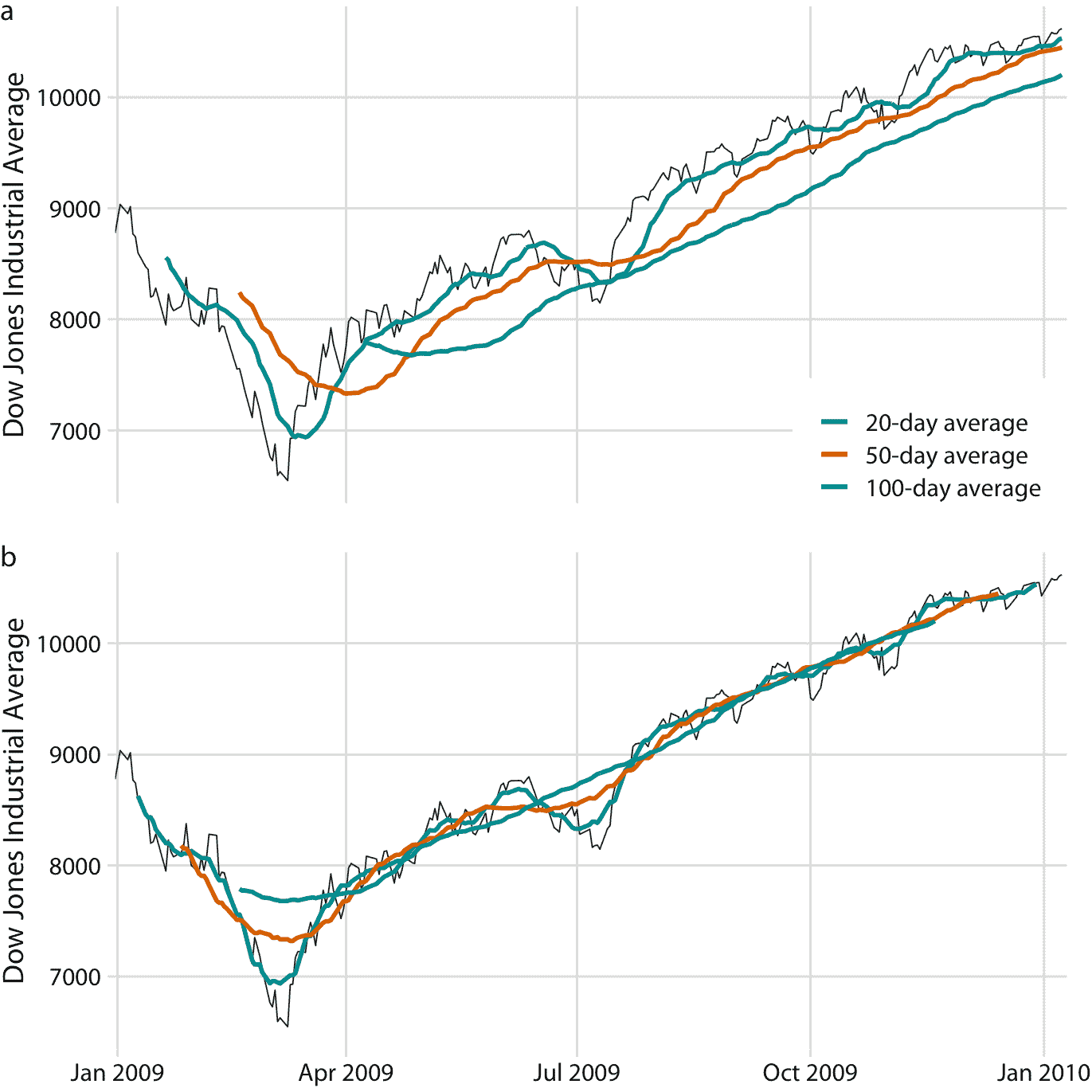
圖 14.2:2009 年道瓊斯工業平均指數的每日收盤價,以及 20 天,50 天和 100 天移動平均值。(a)移動平均值繪制在移動時間窗口的末尾。(b)移動平均值繪制在移動時間窗口的中心。數據來源:雅虎金融
無論我們繪制具有或不具有滯后的平滑時間序列,我們都可以看到,我們計算平均的時間窗口的長度,設置了在平滑曲線中保持可見的波動規模。 20 日移動平均值僅消除小的短期峰值,但其他方面也緊隨日常數據。另一方面,100 天移動平均值甚至可以消除在數周時間內出現的相當大幅度的下跌或峰值。例如,2009 年第一季度到 7000 點以下的大幅下跌,對于 100 日移動平均值是不可見的,取而代之的是不會低于 8000 點的溫和曲線(圖 14.2 )。同樣,2009 年 7 月左右的下跌在 100 日移動平均值中完全看不到。
移動平均值是最簡單的平滑方法,它有一些明顯的局限性。首先,它導致平滑的曲線比原始曲線短(圖 14.2 )。開頭或結尾部分或兩者都缺失。并且時間序列被平滑得越多(即,平均窗口越大),平滑曲線越短。其次,即使平均窗口較大,移動平均值也不一定平滑。即使已經實現了更大規模的平滑,它也可能表現出小的凸起和擺動(圖 14.2)。這些擺動是由進入或退出平均窗口的各個數據點引起的。由于窗口中的所有數據點均等加權,因此窗口邊界處的各個數據點可能對平均值產生明顯影響。
統計學家已經開發了許多平滑方法,以減輕移動平均值的缺陷。這些方法復雜得多且計算成本高,但它們在現代統計計算環境中很容易獲得。一種廣泛使用的方法是 LOESS(局部估計的散點圖平滑, W. S. Cleveland(1979)),它將低階多項式擬合到數據的子集。重要的是,每個子集中心的點比邊界點的權重更重,這種加權方案產生的結果比加權平均值更平滑(圖 14.3 )。此處顯示的 LOESS 曲線看起來類似于 100 天平均值,但不應過度解釋這種相似性。可以通過調整參數來調整 LOESS 曲線的平滑度,并且不同的參數選擇會使 LOESS 曲線看起來更像 20 天或 50 天的平均值。
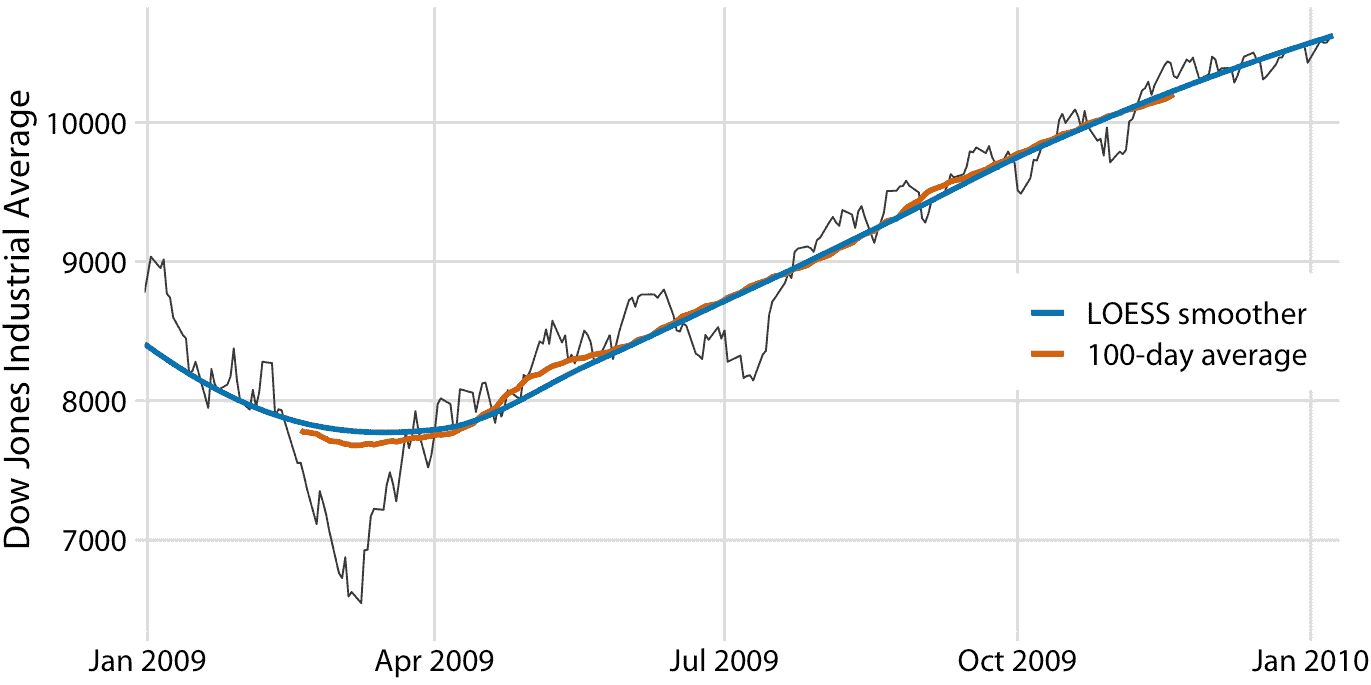
圖 14.3:圖 14.2 道瓊斯數據的 LOESS 擬合與 100 天移動平均值的比較。 LOESS 平滑顯示的整體趨勢幾乎與 100 天移動平均值相同,但 LOESS 曲線更平滑,并且延伸到整個數據范圍。數據來源:雅虎金融
重要的是,LOESS 不僅限于時間序列。它可以應用于任意散點圖,從其名稱“局部估計的散點圖平滑”可以看出。例如,我們可以使用 LOESS 來尋找汽車油箱容量與其價格之間關系的趨勢(圖 14.4)。 LOESS 序列顯示,油箱容量與廉價汽車(低于 20,000 美元)的價格大致成線性增長,但是對于更昂貴的汽車而言,它保持不變。超過大約 20,000 美元,購買更昂貴的汽車將不會讓你擁有一個更大的油箱。

圖 14.4:1993 年車型的 93 輛汽車的油箱容量與價格。每個點對應一輛汽車。實線表示數據的 LOESS 平滑。我們看到油箱容量相對于價格近似線性增加,直到約 20,000 美元的價格,然后穩定下來。數據來源:圣勞倫斯大學 Robin H. Lock
LOESS 是一種非常流行的平滑方法,因為它往往會產生適合人眼的效果。但是,它需要擬合許多單獨的回歸模型。這使得其對于大型數據集較慢,即使在現代計算設備上也是如此。
作為 LOESS 的更快替代品,我們可以使用樣條模型。樣條曲線是一種分段多項式函數,它具有高度的靈活性,但總是看起來很平滑。使用樣條線時,我們會遇到術語“結”。樣條曲線中的結是各個樣條曲線段的端點。如果我們使用 *k* 段擬合樣條曲線,我們需要指定 *k* + 1 個結。雖然樣條擬合在計算上是有效的,特別是如果結的數量不是太大,樣條有其自身的缺點。最重要的是,存在一系列令人眼花繚亂的不同類型的樣條曲線,包括三次樣條曲線,B 樣條曲線,薄板樣條曲線,高斯過程樣條曲線以及其他許多樣條曲線,選擇哪個可能并不明顯。樣條類型和使用的結數的具體選擇,可能導致相同數據的平滑函數大不相同(圖 14.5 )。

圖 14.5:不同的平滑模型表現出極大不同的行為,特別是在數據邊界附近。 (a)LOESS 更平滑,如圖 14.4。(b)具有 5 個結的立方回歸樣條。 (c)具有 3 個結的薄板回歸樣條。(d)高斯過程樣條,6 個結。數據來源:圣勞倫斯大學 Robin H. Lock
大多數數據可視化軟件將提供平滑功能,可能實現為一種局部回歸(如 LOESS)或一種樣條曲線。平滑方法可以稱為 GAM,廣義附加模型,它是所有這些類型的平滑器的超集。重要的是要注意,平滑特征的輸出高度依賴于適合的特定 GAM 模型。除非您嘗試了許多不同的選擇,否則您可能永遠不會意識到,您看到的結果在多大程度上取決于統計軟件所做的特定默認選擇。
在解釋平滑函數的結果時要小心。可以通過許多不同方式平滑相同的數據集。
## 14.2 以所定義的函數形式顯示趨勢
我們在圖 14.5 中看到,對于任何給定的數據集,通用平滑器的行為可能有些不可預測。這些平滑器也不提供具有有意義的解釋的參數估計值。因此,只要有可能,最好使用適合于數據的特定函數形式擬合曲線,并使用具有明確含義的參數。
對于油箱數據,我們需要一條曲線,該曲線最初線性上升但隨后以恒定值平穩。函數`y = A - B exp(-mx)`可能適合該順序。這里,`A`,`B`和`m`是常數,我們調整它來使曲線適合數據。對于較小的`x`,函數近似為線性,`y ~ A - B + B mx`,對于較大`x`,它接近常數值,`y ~ A`,對于`x`的所有制它嚴格遞增。圖 14.6 表明該方程至少與我們之前考慮的任何平滑器一樣適合數據(圖 14.5)。
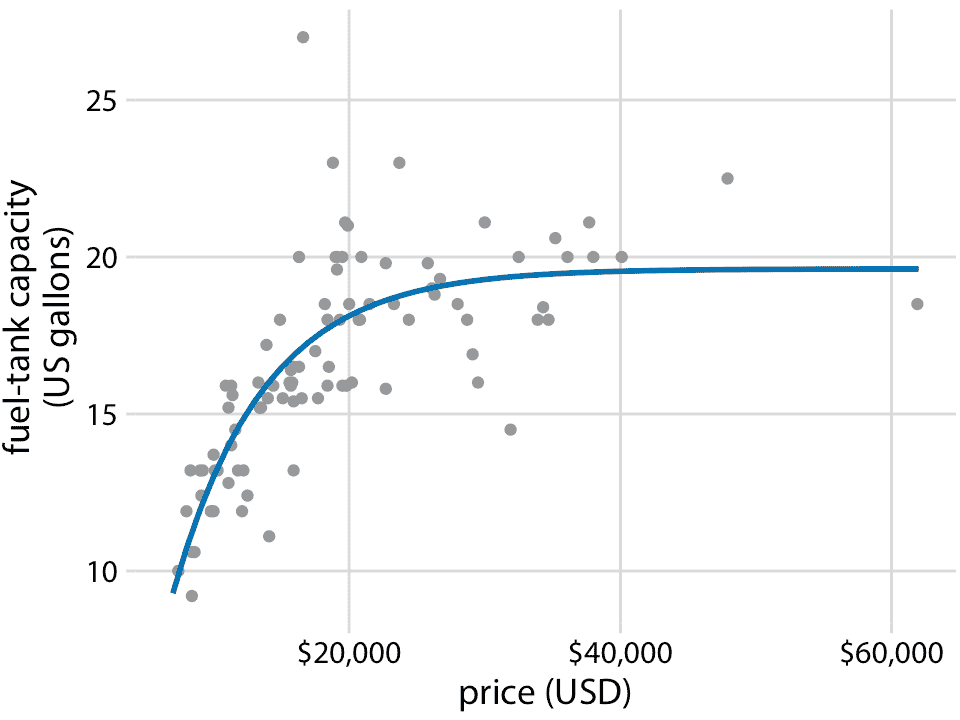
圖 14.6:用明確的分析模型表示的油箱數據。實線對應于公式`y = A-B exp(-mx)`與數據的最小二乘擬合。擬合參數為`A = 19.6 `,`B = 29.2`,`m = 0.00015 `。數據來源:圣勞倫斯大學 Robin H. Lock
在許多不同的上下文中適用的函數形式是簡單的直線, `y = A + mx`。在現實世界的數據集中,兩個變量之間的近似線性關系非常常見。例如,在第 12 章中,我討論了藍鳥的頭長和體重之間的關系。這種關系對于雌鳥和雄鳥都是近似線性的,并且在散點圖中,在點之上繪制線性趨勢線,有助于讀者感知趨勢(圖 14.7)。
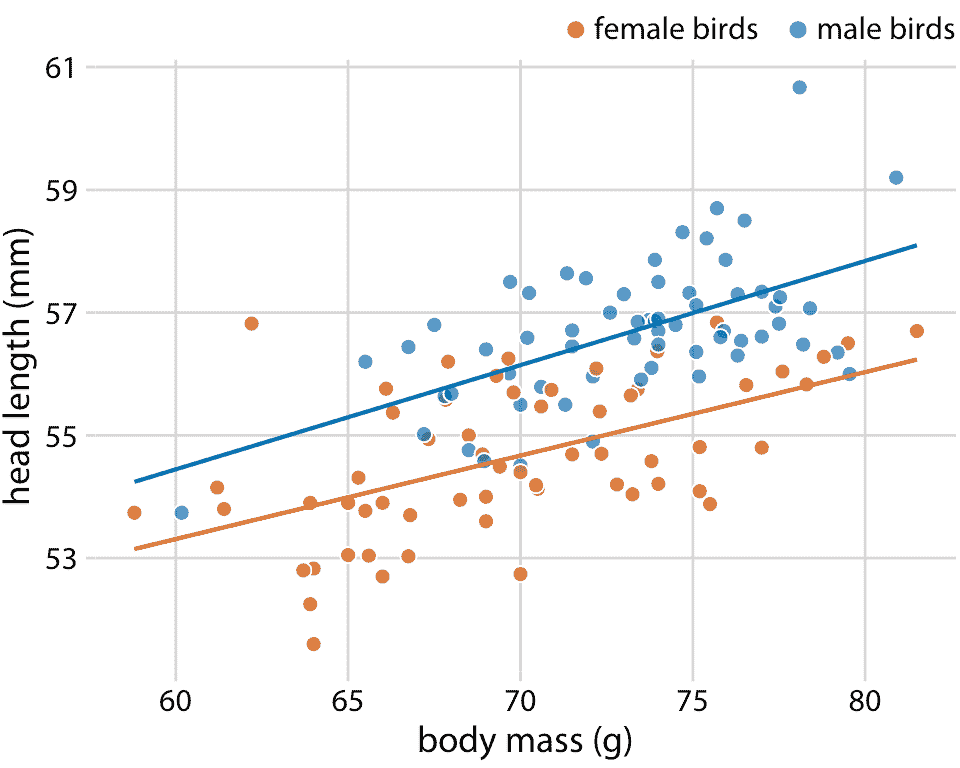
圖 14.7:123 只藍鳥的頭長與體重的關系。鳥的性別用顏色表示。這個圖形相當于圖 12.2,但現在我們已經在各個數據點之上繪制了線性趨勢直線。數據來源:歐柏林學院的 Keith Tarvin
當數據表現出非線性關系時,我們需要猜測適當的函數形式可能是什么。在這種情況下,通過轉換軸使線性關系出現,我們可以評估我們猜測的準確性。為了證明這一原理,讓我們回到預印本服務器 bioRxiv 的每月提交量,在第 12 章中討論。如果每個月提交量的增量與上個月的提交量成比例,即,如果每月的提交量以一個固定的百分比增長,那么得到的曲線是指數的。 bioRxiv 數據似乎滿足了這個假設,因為指數形式的曲線`y = A exp(mx)`,很好地符合 bioRxiv 提交數據(圖 14.8)。
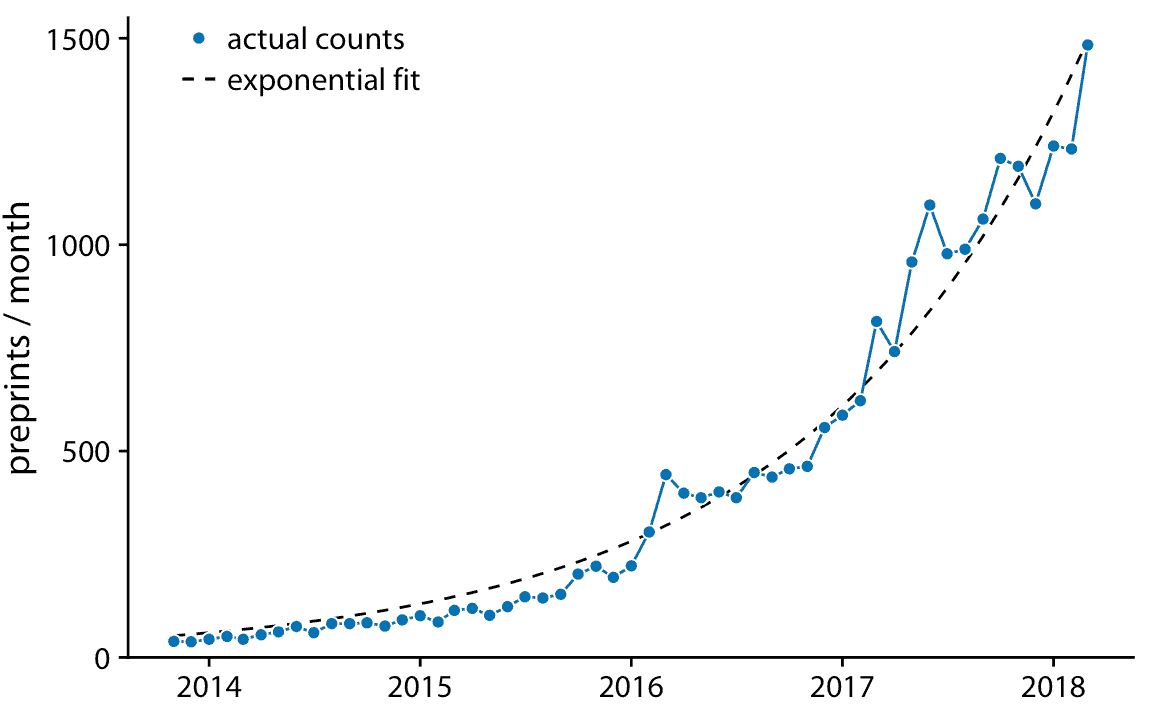
圖 14.8:預印本服務器 bioRxiv 的每月提交量。藍色實線表示預印本的實際的每月計數,黑色虛線表示數據的指數擬合,`y = 60 exp(0.77(x - 2014))`。數據來源:Jordan Anaya,[prepubmed.org](http://www.prepubmed.org/)
如果原始曲線是指數,`y = A exp(mx)`,則 *y* 值的對數變換將使其變為線性關系,`log(y) = log(A) + mx`。因此,使用對數變換的 *y* 值(或等效地,使用對數 *y* 軸)繪制數據并尋找線性關系,是確定數據集是否呈現指數增長的好方法。對于 bioRxiv 提交圖形,當使用對數 *y* 軸時,我們確實獲得了線性關系(圖 14.9)。
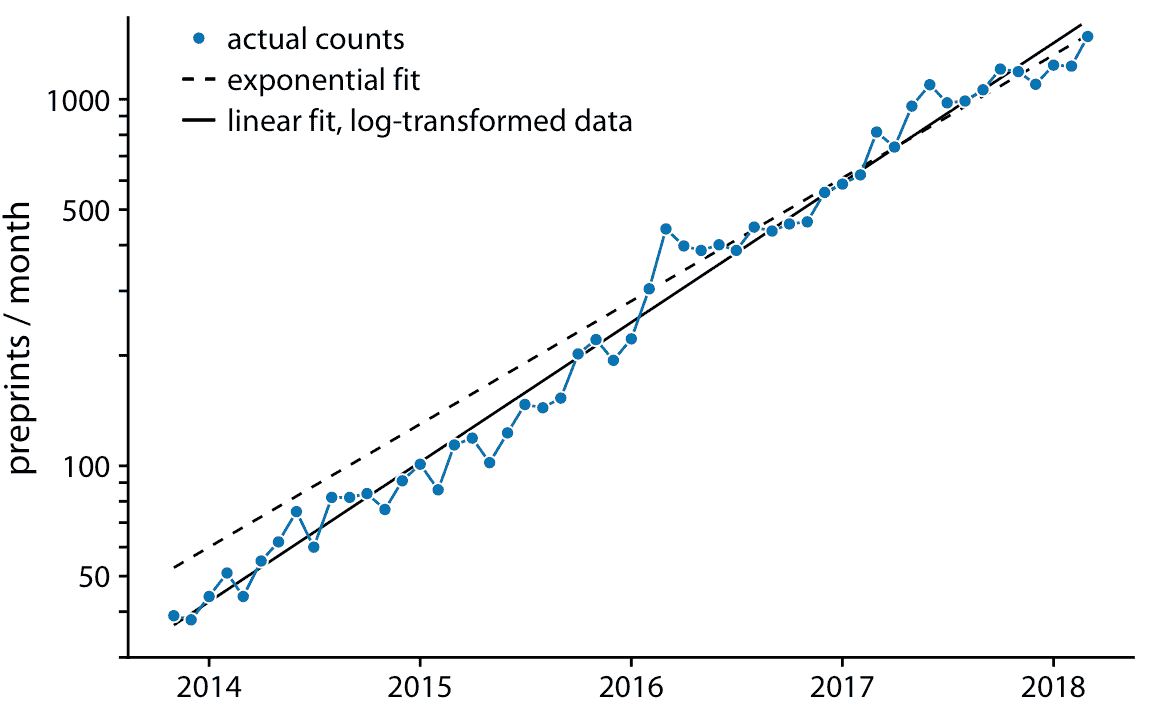
圖 14.9:預印本服務器 bioRxiv 每月提交量,以對數刻度顯示。藍色實線表示預印本的實際的每月計數,黑色虛線表示圖 14.8 的指數擬合,黑色實線表示對數變換數據的線性擬合,對應于`y = 43 exp(0.88(x - 2014))`。數據來源:Jordan Anaya,[prepubmed.org](http://www.prepubmed.org/)
在圖 14.9 中,除了實際提交計數外,我還顯示了圖 14.8 的指數擬合以及對數變換數據的線性擬合。這兩種擬合相似但不相同。特別是,虛線的斜率似乎略微偏離。在一半時間序列中,該線系統地高于各個數據點。這是指數擬合的常見問題:對于最大數據值,從數據點到擬合曲線的平方偏差與最小數據值相比要大得多,因為最小數據值的偏差對總和平方的貢獻很小適合度最小化。結果,擬合直線系統地高于或低于最小數據值。出于這個原因,我通常建議避免指數擬合,而是在對數變換數據上使用線性擬合。
通常,將直線擬合到變換數據,比將非線性曲線擬合到未變換數據更好。
圖 14.9 的圖通常被稱為對數線性的,因為 *y* 軸是對數的, *x* 軸是線性的。我們可能遇到的其他圖包括雙對數,其中 *y* 和 *x* 軸都是對數,或線性對數,其中 *y* 是線性的, *x* 是對數的。在雙對數圖中,`y ~ x ^ alpha`形式的冪律顯示為直線(例如,參見圖 8.7),線性對數圖,`y ~ log(x)`形式的對數關系顯示為直線。其他函數形式可以通過更專業的坐標轉換,轉換為線性關系,但這三種(對數線性,雙對數,線性對數)涵蓋了廣泛的實際應用。
## 14.3 趨勢和時間序列分解
對于具有突出長期趨勢的任何時間序列,刪除此趨勢來特別突出任何顯著??偏差可能是有用的。這種技術被稱為去趨勢 ,我將在這里用房價來證明它。在美國,抵押貸款機構 Freddie Mac 發布月度指數,稱為 Freddie Mac 房價指數,它跟蹤房價隨時間的變化。該指數試圖捕捉給定區域中整個房屋市場的狀態,因此,例如 10% 的指數增加可以被解釋為,相應市場中的平均房價增加 10% 。該指數在 2000 年 12 月任意設定為 100。
在很長一段時間內,房價往往呈現出一致的年增長率,與通貨膨脹基本一致。然而,覆蓋這一趨勢的是房地產泡沫,導致嚴重的繁榮和蕭條周期。圖 14.10 顯示了美國四個州的實際房價指數及其長期趨勢。我們看到,在 1980 年到 2017 年之間,加利福尼亞經歷了兩次泡沫,一次是在 1990 年,一次是在 2000 年代中期。在同一時期,內華達州在 2000 年代中期只經歷過一次泡沫,德克薩斯州和西弗吉尼亞州的房價一直緊跟其長期趨勢。因為房價傾向于以增量的百分比增長,即指數增長,所以我在圖 14.10 中選擇了對數 *y* 軸。直線相當于加利福尼亞州年度價格增長的 4.7%,內華達州,德克薩斯州和西弗吉尼亞州年度價格增長的 2.8%。
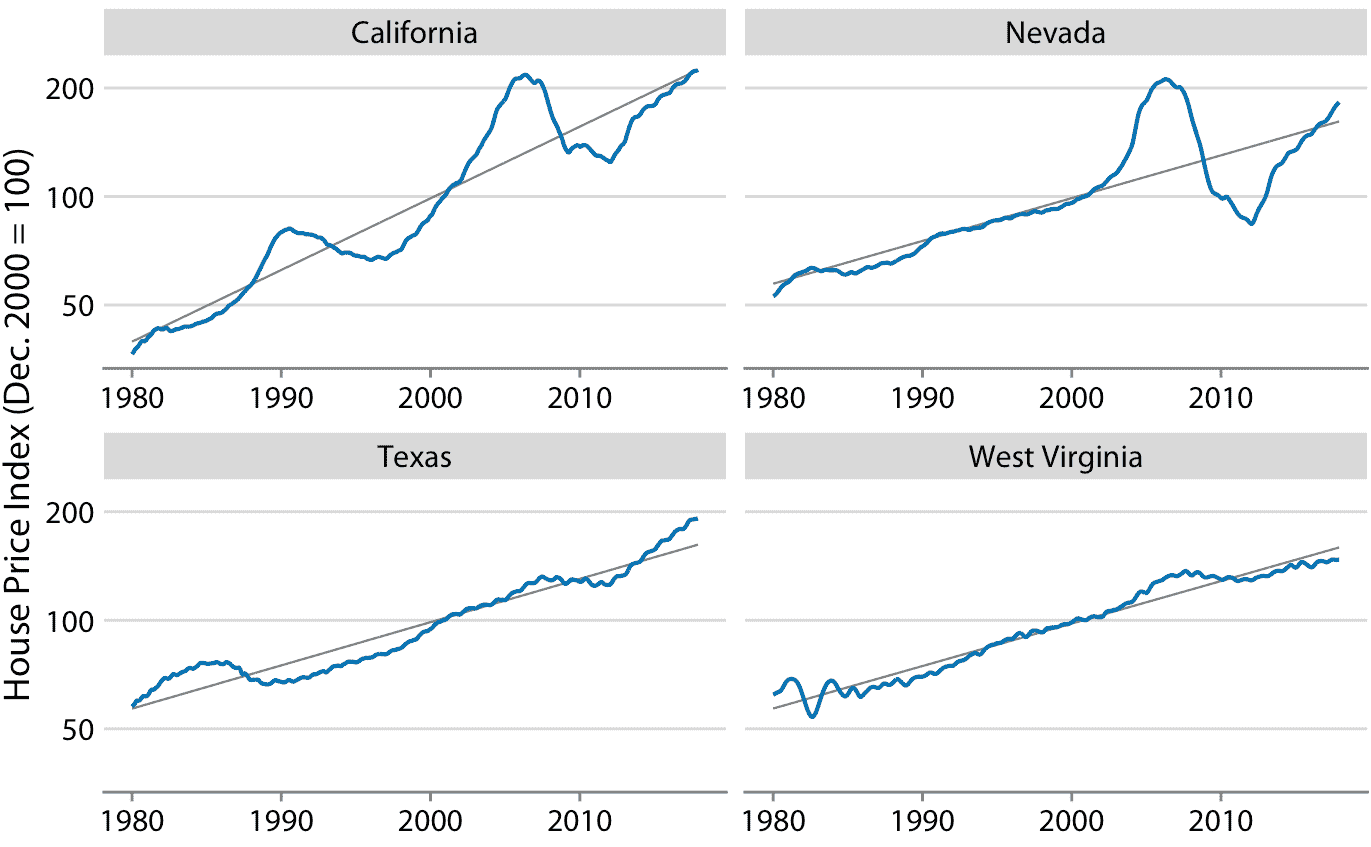
圖 14.10:1980 年至 2017 年 Freddie Mac 房價指數,顯示四個選定州(加利福尼亞州,內華達州,德克薩斯州和西弗吉尼亞州)。房價指數是一個無單位數字,用于跟蹤所選地理區域內的相對房價。該指數任意縮放,使其在 2000 年 12 月等于 100。藍線表示指數的月度波動,而灰色直線表示各州的長期價格趨勢。注意, *y* 軸是對數的,因此灰色直線代表一致的指數增長。數據來源:房地美房價指數
我們通過將每個時間點的實際價格指數,除以長期趨勢中的相應值來抵消住房價格。在視覺上,這個除法看起來像是從圖 14.10 中的藍線中減去灰線,因為未轉換值的除法相當于對數轉換值的減法。由此產生的去趨勢房屋價格更清晰地顯示房屋泡沫(圖 14.11 ),因為趨勢強調了時間序列中的意外移動。例如,在原始時間序列中,加利福尼亞州從 1990 年到 1998 年的房價下跌看起來不大(圖 14.10 )。但是,在同一時期,根據長期趨勢,我們預計價格會上漲。相對于預期的上漲,價格下跌幅度很大,在最低點達到 25%(圖 14.11)。
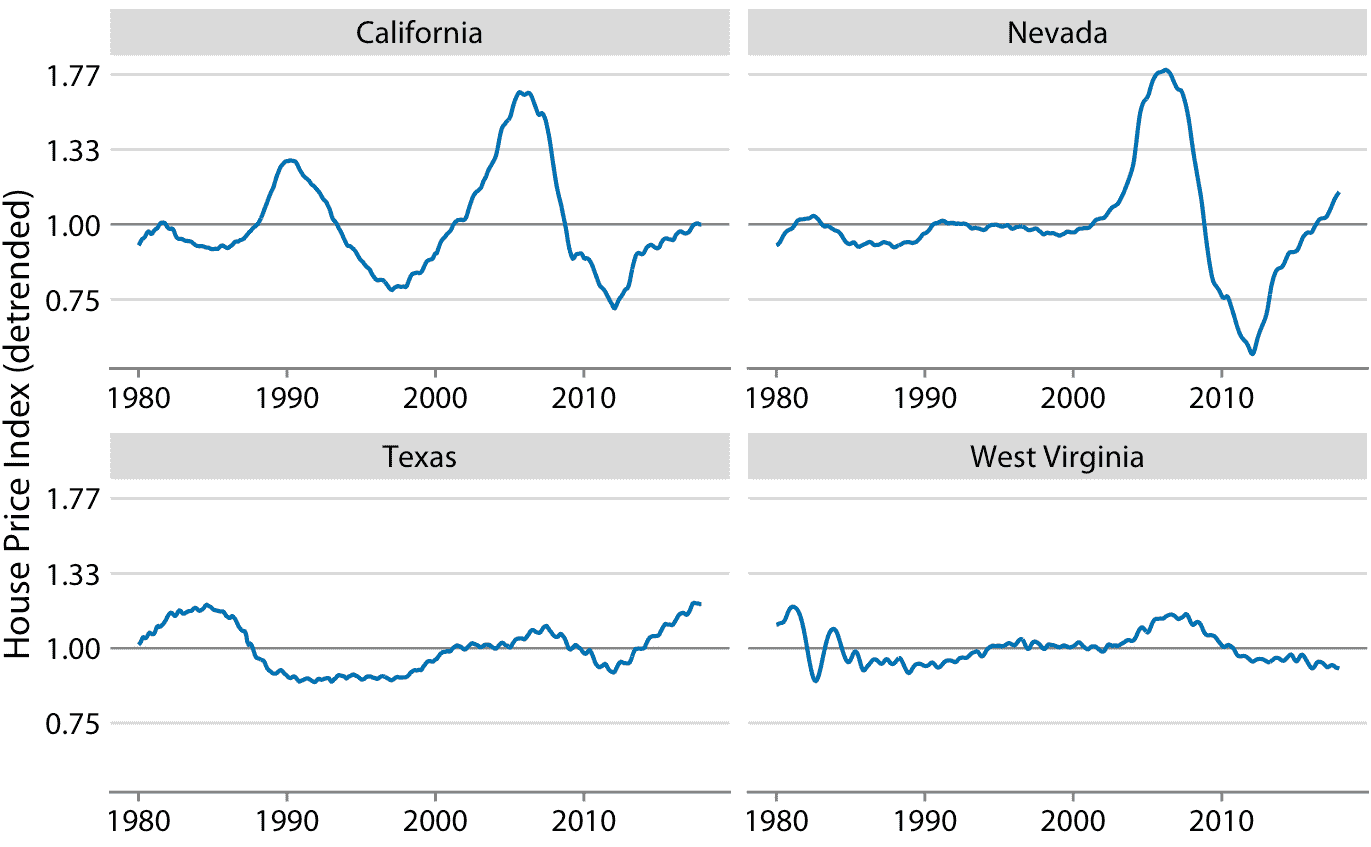
圖 14.11:Freddie Mac 房屋價格指數的去趨勢版本如圖 14.10 所示。通過將實際指數(圖 14.10 中的藍線)除以基于長期趨勢的預期值(圖 14.10 中的直灰線)來計算去趨勢指數。這種可視化表明,加利福尼亞經歷了兩次房地產泡沫,大約在 1990 年和 2000 年代中期,可以通過相對于長期趨勢的預期的實際房價的快速上漲和隨后的下降來確定。同樣,內華達州在 2000 年代中期經歷了一次房地產泡沫,德克薩斯州和西弗吉尼亞州都沒有經歷過太多的泡沫。數據來源:Freddie Mac 房價指數
除了簡單的去趨勢之外,我們還可以將時間序列分成多個不同的成分,以便它們的總和復原原始時間序列。一般而言,除了長期趨勢外,還有三個不同的成分可能影響時間序列。首先,存在隨機噪聲,這會導致小的上下不穩定運動。在本章所示的所有時間序列中都可以看到這種噪聲,但可能在圖 14.9 中最清楚。其次,可能會有獨特的外部事件在時間序列中留下痕跡,例如圖 14.10 中所見的明顯的房屋泡沫。第三,可能存在周期性變化。例如,室外溫度表現出每日周期性變化。下午早些時候溫度最高,清晨溫度最低。室外溫度也顯示出每年的周期性變化。它們傾向于在春季上升,在夏季達到最大值,然后在秋季下降并在冬季達到最小值(圖 3.2 )。
為了證明時間序列不同成分的概念,我將在此處分解基林曲線,其顯示 CO2 豐度隨時間的變化(圖 14.12)。 CO2 以百萬分率(ppm)測量。我們看到 CO2 豐度的長期增長略快于線性,從 20 世紀 60 年代的 325 ppm 以下到 21 世紀第二個十年的 400 以上(圖 14.12)。 CO2 豐度也具有年度波動,在整體增長之上遵循一致的上下模式。年度波動是由北半球的植物生長推動的。植物在光合作用期間消耗 CO2 。由于全球大部分陸地都位于北半球,而且春季和夏季植物生長最活躍,我們看到全球大氣 CO2 的年度下降與北半球的夏季月份相重合。
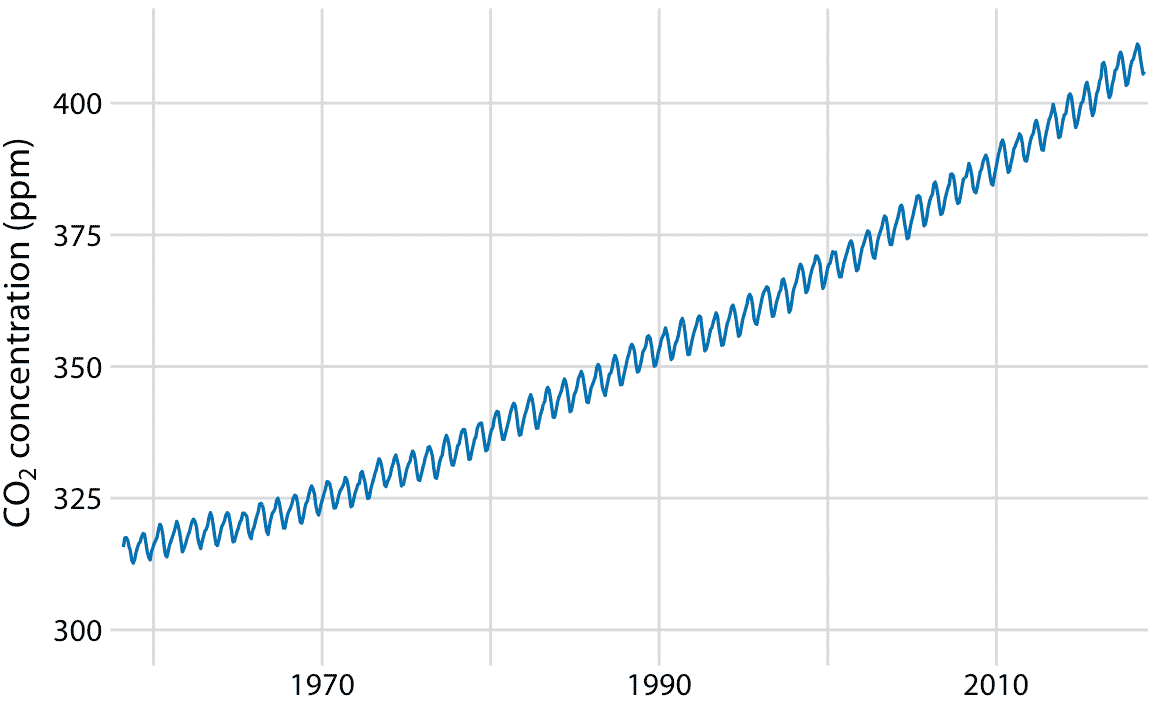
圖 14.12:基林曲線。基林曲線顯示了大氣中 CO2 豐度隨時間的變化。自 1958 年以來,CO2 的豐度一直在夏威夷的莫納羅亞天文臺進行監測,最初是在 Charles Keeling 的指導下進行的。這里顯示的是月平均 CO2 讀數,以百萬分率(ppm)表示。 CO2 讀數隨季節而波動,但顯示出一致的長期增長趨勢。數據來源:NOAA/ESRL 的 Pieter Tans 博士和 Scripps 海洋學研究所的 Ralph Keeling 博士
我們可以將基林曲線分解為長期趨勢,季節性波動和剩余部分(圖 14.13 )。我在這里使用的具體方法稱為 STL(使用 LOESS 的時間序列的季節性分解,RB Cleveland 等人,1990),但還有許多其他方法可以實現類似目標。分解表明,在過去的三十年中,CO2 豐度增加了 50ppm 以上。相比之下,季節性波動小于 8 ppm(相對于長期趨勢,它們永遠不會導致增加或減少超過 4 ppm),其余則小于 1.6 ppm(圖 14.13)。剩余部分是實際讀數與長期趨勢和季節性波動之和之間的差異,這里它對應于每月 CO2 讀數中的隨機噪聲。然而,更一般地,剩余部分也可以捕獲獨特的外部事件。例如,如果大規模的火山爆發釋放出大量的 CO2,這種事件可能會被看作是剩余部分的突然飆升。圖 14.13 表明,近幾十年來沒有這種獨特的外部事件對基林曲線產生重大影響。
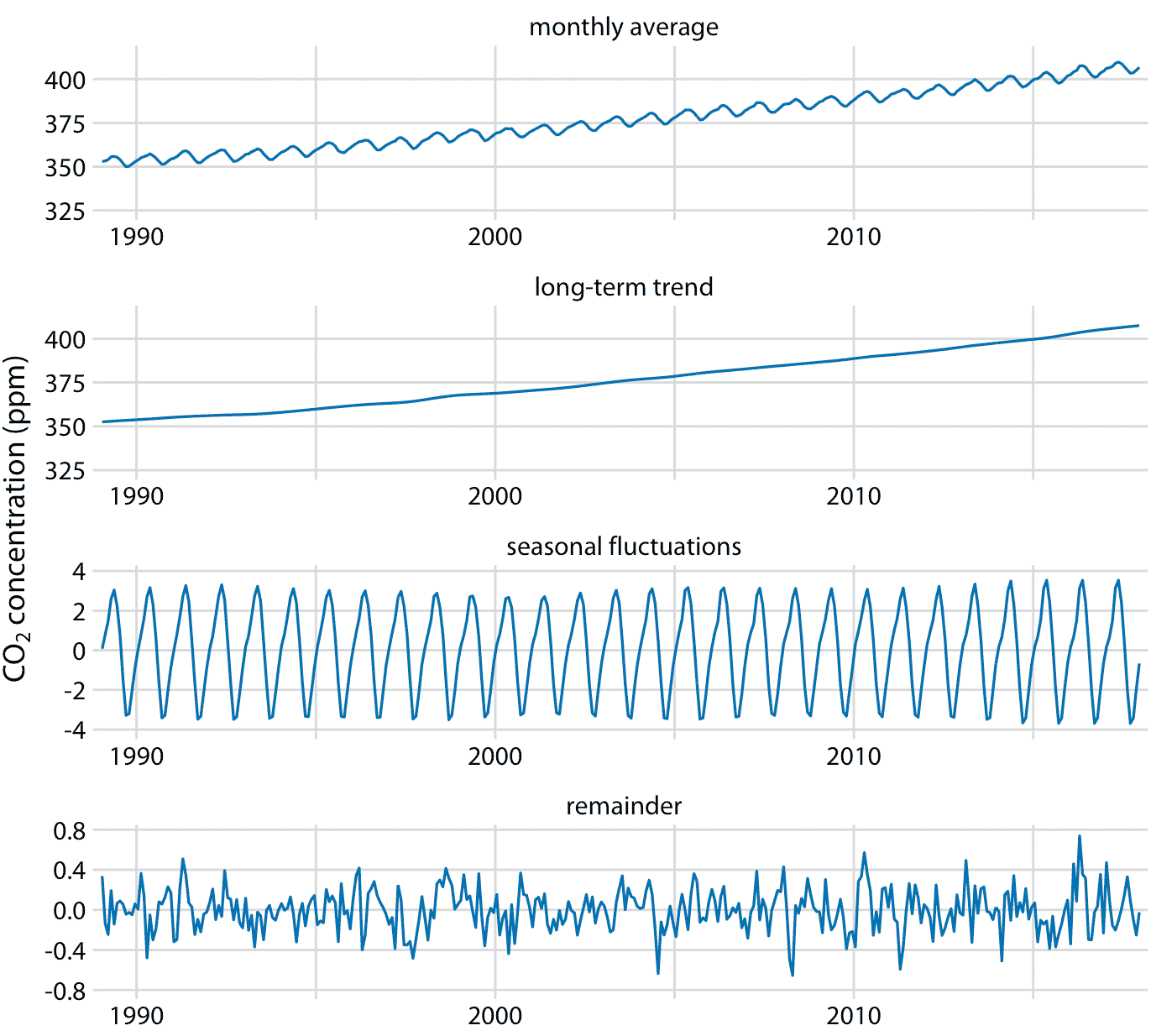
圖 14.13:基林曲線的時間序列分解,顯示月平均值(如圖 14.12 ),長期趨勢,季節性波動和剩余部分。剩余部分是實際讀數與長期趨勢和季節波動之和的差異,它代表隨機噪聲。我已經縮放到最近 30 年的數據,以更清楚地顯示年度波動的形狀。數據來源:NOAA/ESRL 的 Pieter Tans 博士和 Scripps 海洋學研究所的 Ralph Keeling 博士
### 參考
```
Cleveland, W. S. 1979. “Robust Locally Weighted Regression and Smoothing Scatterplots.” Journal of the American Statistical Association 74: 829–36.
Cleveland, R. B., W. S. Cleveland, J. E. McRae, and I. Terpenning. 1990. “STL: A Seasonal-Trend Decomposition Procedure Based on Loess.” Journal of Official Statistics 6: 3–73.
```
- 數據可視化的基礎知識
- 歡迎
- 前言
- 1 簡介
- 2 可視化數據:將數據映射到美學上
- 3 坐標系和軸
- 4 顏色刻度
- 5 可視化的目錄
- 6 可視化數量
- 7 可視化分布:直方圖和密度圖
- 8 可視化分布:經驗累積分布函數和 q-q 圖
- 9 一次可視化多個分布
- 10 可視化比例
- 11 可視化嵌套比例
- 12 可視化兩個或多個定量變量之間的關聯
- 13 可視化自變量的時間序列和其他函數
- 14 可視化趨勢
- 15 可視化地理空間數據
- 16 可視化不確定性
- 17 比例墨水原理
- 18 處理重疊點
- 19 顏色使用的常見缺陷
- 20 冗余編碼
- 21 多面板圖形
- 22 標題,說明和表格
- 23 平衡數據和上下文
- 24 使用較大的軸標簽
- 25 避免線條圖
- 26 不要走向 3D
- 27 了解最常用的圖像文件格式
- 28 選擇合適的可視化軟件
- 29 講述一個故事并提出一個觀點
- 30 帶注解的參考書目
- 技術注解
- 參考
